上承式加V拱桥动力特性研究及试验验证

谢肖礼，庞木林，邱 辰，覃石生

(广西大学 土木建筑工程学院，南宁 530004)

随着我国西部大开发战略的实施与推进，在地形地貌、水文条件极为复杂的西部山区修建高速铁路已成为常态[1].上承式拱桥刚度大、跨越能力强，且能依托地势修建基础，造价较为经济.同时，可根据实际条件因地制宜选取支架拼装、劲性骨架、斜拉扣挂、浮运、转体等施工方法，成为山区高速铁路桥梁的首选桥型[2-5].如目前世界上跨度最大的铁路拱桥——大瑞铁路怒江四线特大桥[6](修建中，主跨达490 m，钢桁拱)，世界上跨度最大的钢筋混凝土拱桥——沪昆高铁北盘江特大桥[7](主跨为445 m)，国内最大跨度的重载铁路拱桥——浩吉铁路洛河大桥[8](主跨为220 m，钢管混凝土拱)等.

西部地区山高坡陡、峡谷众多，铁路线穿越时很多情况下需要修建大跨度桥梁一跨而过，但是跨径增大后，上承式拱桥在L/4(L为桥梁跨径)处由列车静活载所产生的上挠度亦会增加，威胁行车安全.此外，高速铁路桥梁一般以双线或四线为主[9-11]，桥梁宽跨比较小，加之列车荷载大、行驶速度高，因此对桥梁的动力特性要求更高.而上承式拱桥跨径增大后，随着自重的增加，其自振频率下降很快，对列车行进造成不利影响.

现有上承式拱桥的上部结构主要由拱圈和拱上建筑组成，若拱上建筑为空腹式，则通常有两种结构形式[12]：① 梁式拱上建筑的上承式拱桥，由拱圈、立柱(平行布置)和主梁组成，是目前大跨上承式拱桥的常用形式；② 传统上承式桁架拱，由拱圈、中间实腹段、边上桁架和主梁组成，亦有着不俗的跨越能力.从结构布置来看，前者的局部结构为四边形结构，后者则形成了中间弯梁加两边桁架构成的拱桥结构.从结构形式上看，第一种结构形式的立柱与主梁、拱圈构成了连续的四边形，其刚度较小，随着跨度及荷载的不断增加，很容易产生剪切和弯曲变形，从而导致自振频率快速下降.而第二种结构形式桁架参与承担绝大部分恒载，拱的优势无法充分发挥，此外，虽然这种拱桥刚度较大，但多为钢筋混凝土结构或拱片桥，其自重很大且节点开裂问题突出[13]，因而自振频率受自重的负面影响较刚度的正面影响大，故自振频率较低.

桥梁的动力特性是其动力性能分析的基本参数，地震响应分析、风致振动分析以及车桥耦合分析等均需以动力特性为基础[14-15].尽管桥梁的动力特性十分重要，但是国内外专门针对上承式拱桥动力特性的研究不多，目前查阅到的资料主要有：欧碧峰等[16]利用ANSYS研究了拱上建筑形式等对大跨度上承式钢管混凝土拱桥动力特性的影响，对深入认识钢管混凝土拱桥动力特性有一定的参考价值；张强[17]通过ANSYS对杭州千岛湖大桥主桥的动力特性进行了参数敏感性分析，为大跨度上承式钢管混凝土拱桥冲击系数的取值提供了一定依据；曾勇等[18]利用ANSYS对某上承式钢管混凝土拱桥进行了动力特性研究和横向静风响应分析，为研究拱桥面内及面外振动提出了建议；蒋凌杰等[19]运用ANSYS分析了上承式混凝土拱桥的自振特性及其一般规律和影响因素，为此类拱桥动力特性的参数敏感性研究做出了指导；杨伟[20]通过Midas Civil研究了四川玻璃沟大桥的动力特性及其响应行为，为该桥的运营管理提供了一些依据.以上关于上承式拱桥动力特性的研究均基于现有结构形式进行，较少有结构体系创新，对如何改善动力特性这一指标提出的建设性意见不多，不能很好地促进上承式拱桥向前发展.

目前上承式拱桥正不断向超大跨径方向发展[21]，其动力特性对整个桥梁安全的影响度迅速增加，为满足铁路运营安全及行车舒适性要求，并为列车提速、桥梁跨径增大提供前提条件，寻求有效方法改善上承式拱桥的动力特性具有重要意义[22].

本文提出一种新的拱桥结构体系，即上承式加V拱桥，其通过适时的结构体系转换，使拱和桁架分阶段承担荷载.通过提高拱桥的刚度，改善结构的动力特性.通过对结构动力特性进行研究，介绍上承式加V拱桥的结构形式和力学原理，利用跨径为10 m的试验桥进行脉动试验并加以验证，利用有限元软件对其刚度和动力特性进行研究，分析V形构件刚度对结构动力特性的影响，分析V形构件数量对结构温度应力的影响，并对V形构件加入时间不同时拱圈的受力进行探讨.

1 上承式加V拱桥动力特性研究

上承式加V拱桥(见图1)主要由拱圈、主梁、V形构件、立柱及横撑等部分组成，其结构形式如图2所示.

自振频率和振型是桥梁结构动力分析最基本的动力特性，反映了结构的质量和刚度分布，与结构组成体系、材料类型、边界条件等有关[23-24].

综上可知，结构的自振频率与刚度成正比而与质量成反比.因此，提高结构刚度或减小结构质量均可增大拱桥的自振频率.

基于以上分析，本文从提高结构的刚度方面实现提高上承式拱桥自振频率的目标.具体思路为：利用现有上承式拱桥主梁与拱圈有一定空间距离的特点，将它们作为上、下弦杆，并在两者间增设适量的V形构件形成桁架结构.由于主梁和拱圈的截面刚度相差不大，因此通过V形构件将两者连在一起形成的桁架能很好地工作.此外，新结构的桁高显著增大而加强了结构的抗弯能力，故而可通过适时的体系转换，使二期恒载及活载由桁架承担，以减轻拱圈负担.由于新结构以桁架来承担活载，从而结构的刚度大幅提高，且在L/4处，列车静活载所产生的上挠度几乎为0，自振频率亦随之提高.另外，V形构件的增设可为拱圈卸载，故可减少拱圈的用钢量，因此新结构总用钢量是可控的，且V形构件的施工在现有上承式拱桥成桥后进行，并未增加施工难度.

1.1 利用三角形稳定性提高拱圈及主梁刚度

上承式加V拱桥在拱圈与主梁间增设若干个V形构件，使其与拱圈和主梁构成多个三角形结构，以此对主梁与拱圈进行有效约束，增加两者的线刚度，进而提高结构的整体刚度.三角形稳定性基于三角形受节点力作用，使其处于轴向变形状态.由于活载的作用点不唯一，会导致以上形成的三角形受非节点力作用，故稳定性会降低，但是立柱对主梁提供的弹性约束可提高其线刚度并减少剪切及弯曲变形，使三角形均能保证有良好的稳定性.因此，利用三角形稳定性可提高拱圈及主梁的线刚度，进而明显提高桥梁自振频率.

1.2 V形构件的合理设置

合理设置V形构件对提高结构的刚度至关重要.为此，需对结构在不同荷载作用下的变形进行研究.主梁在恒载作用下的位移曲线如图3所示.图中：W1为主梁下挠度,Wmax为桥梁在荷载作用下的最大下挠度，其最大变形位置发生在跨中.拱圈在活载作用下的下挠位移包络图如图4所示.图中：W2为拱圈下挠度，其最大位移发生在L/4和3L/4附近.结合以上分析，在设置V形构件时，力求通过其3个角点对拱圈均匀约束，提高拱圈的线刚度.此外，需保证有角点落于拱圈位移包络图的最大位移处和主梁跨中处，以达到加强薄弱点的目的.

图3 恒载作用下主梁挠度Fig.3 Main girder deflection at dead load

图4 活载作用下拱圈下挠位移包络图Fig.4 Envelope diagram of down deflection displacement of arch ribs at live load

此外，增设V形构件会使结构的超静定次数增加，若V形构件数量过多，则温度应力会迅速增加，对结构受力不利，且数量增加时结构的质量也会大幅增长，既不经济也不利于提高结构的自振频率.若V形构件数量过少，则无法为拱圈及主梁提供足够的约束，对结构刚度的提高贡献不大，亦不能有效增大结构的自振频率.因此，需根据跨度及实际需要对V形构件的数量进行科学选取，以达到刚度要求与温度应力响应之间的平衡.

1.3 适时加入V形构件以充分发挥拱受力的优越性

依照目前上承式拱桥的设计方法，恒载和活载均由拱圈承担，然而两者对拱圈产生的内力和变形不同，前者对拱圈产生的效果为小偏心受压，后者为受压、弯曲、剪切及扭转变形.另外，随着活载和跨径的增加，拱圈的力学性能会快速下降.为解决该问题，上承式加V拱桥依照现有上承式拱桥体系成桥后，再加入V形构件完成体系转换，然后再加上二期恒载，最终成桥，故可实现拱和桁架分阶段工作的目标，即一期恒载由拱圈承担，二期恒载及活载则由一个主梁为上弦杆、拱圈为下弦杆、V形构件为腹杆并带多点弹性约束的变高桁架结构来承担，体系转换如图5所示.由此可见，上承式加V拱桥既能充分发挥拱和桁架的优越性，又未增加施工难度.

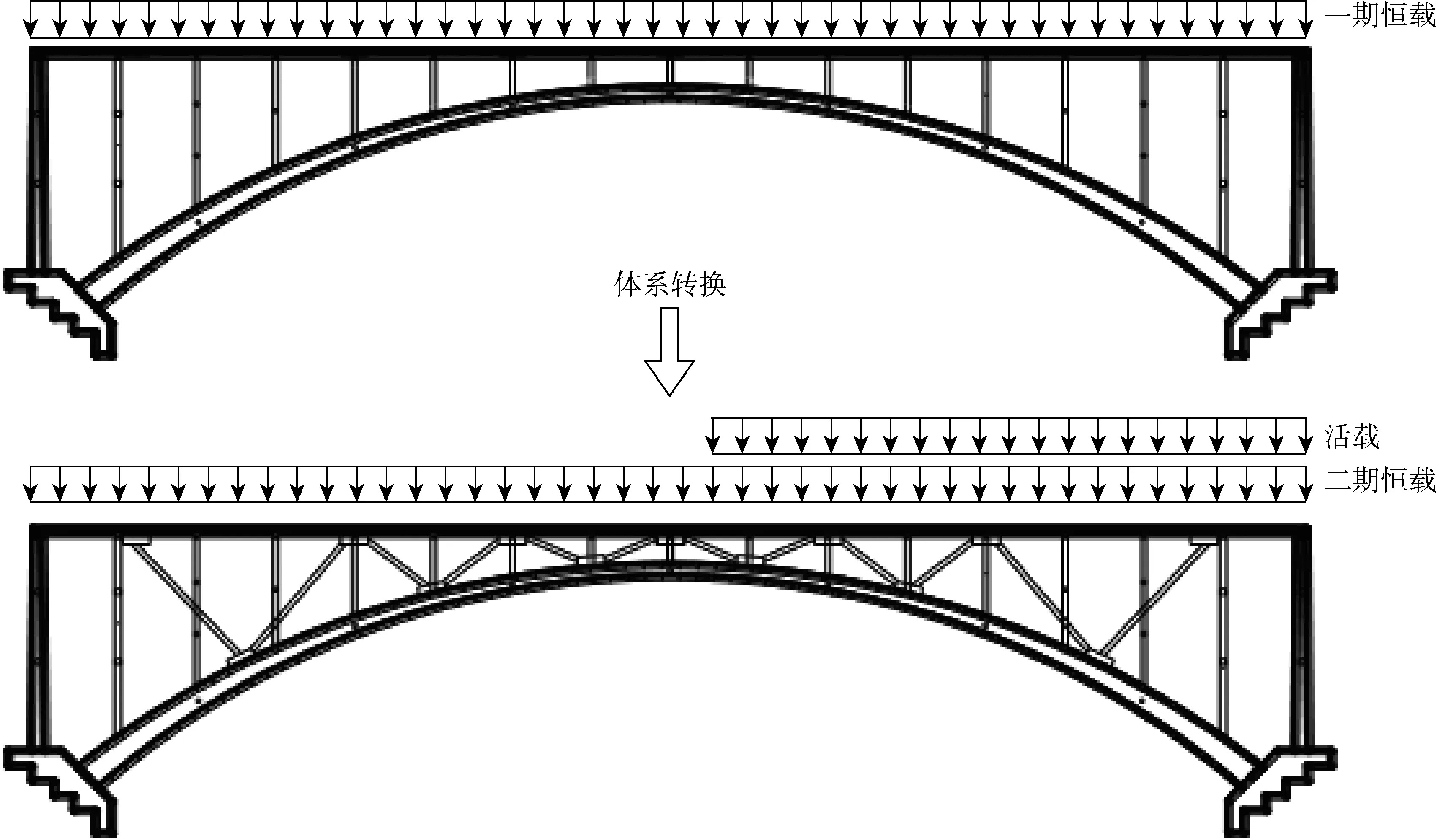
图5 上承式加V拱桥体系转换示意图Fig.5 Schematic diagram of conversion of deck V-arch bridge system

2 上承式加V拱桥试验研究

为了验证上承式加V拱桥动力特性的优越性，修建试验桥进行脉动试验，测试桥梁首次发生面内竖弯的自振频率，并与有限元计算结果进行比对.

2.1 试验桥结构布置及转换方法

试验桥跨径10 m，桥面宽1 m，矢跨比取1/5，拱轴系数为2.8，各构件参数见表1(V形构件及其横撑占总用钢量的8%)，结构布置及试验桥实桥分别如图6和7所示.主梁与立柱和墩台之间设矩形板式橡胶支座，V形构件与主梁和拱圈间采用焊接连接.如图8所示，试验桥采用合二为一的方法进行修建，上承式加V拱桥与现有上承式拱桥间的结构形式转换依靠V形构件上的法兰盘实现.松开法兰盘上的螺栓并取下垫板，V形构件失效，此时结构为现有上承式拱桥；装上垫板并拧紧螺栓，V形构件参与受力，即为上承式加V拱桥.此外，V形构件采用双肢格构式.

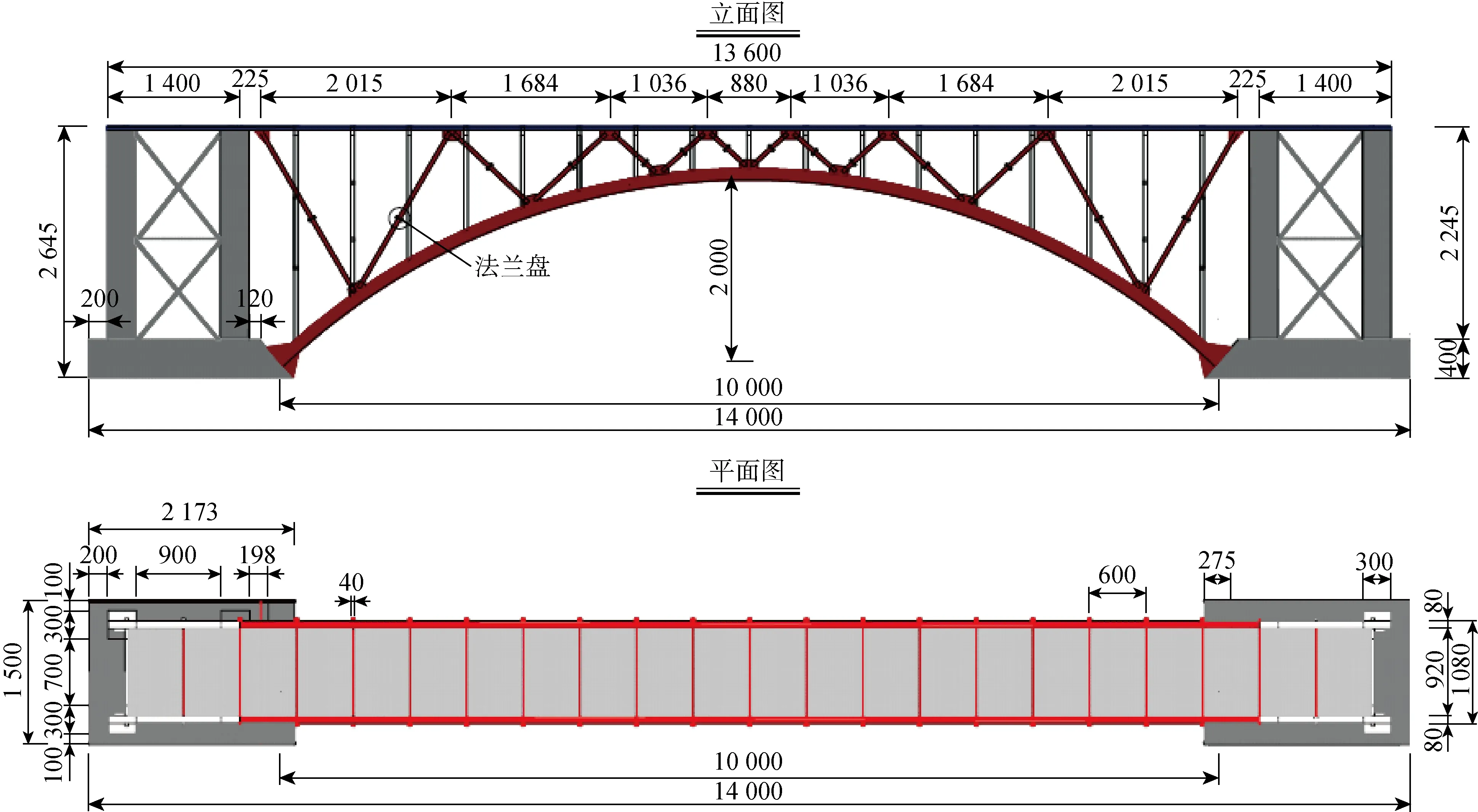
图6 试验桥布置图(mm)Fig.6 Layout of test bridge (mm)

图7 试验桥Fig.7 Test bridge

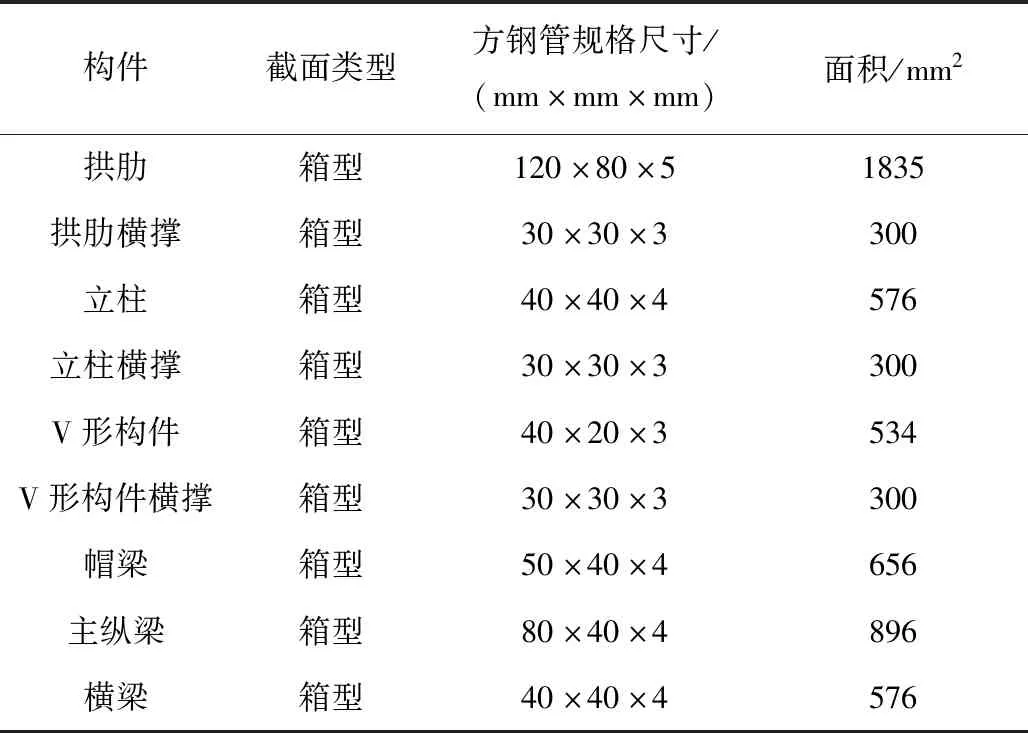
表1 构件参数表Tab.1 Parameters of members

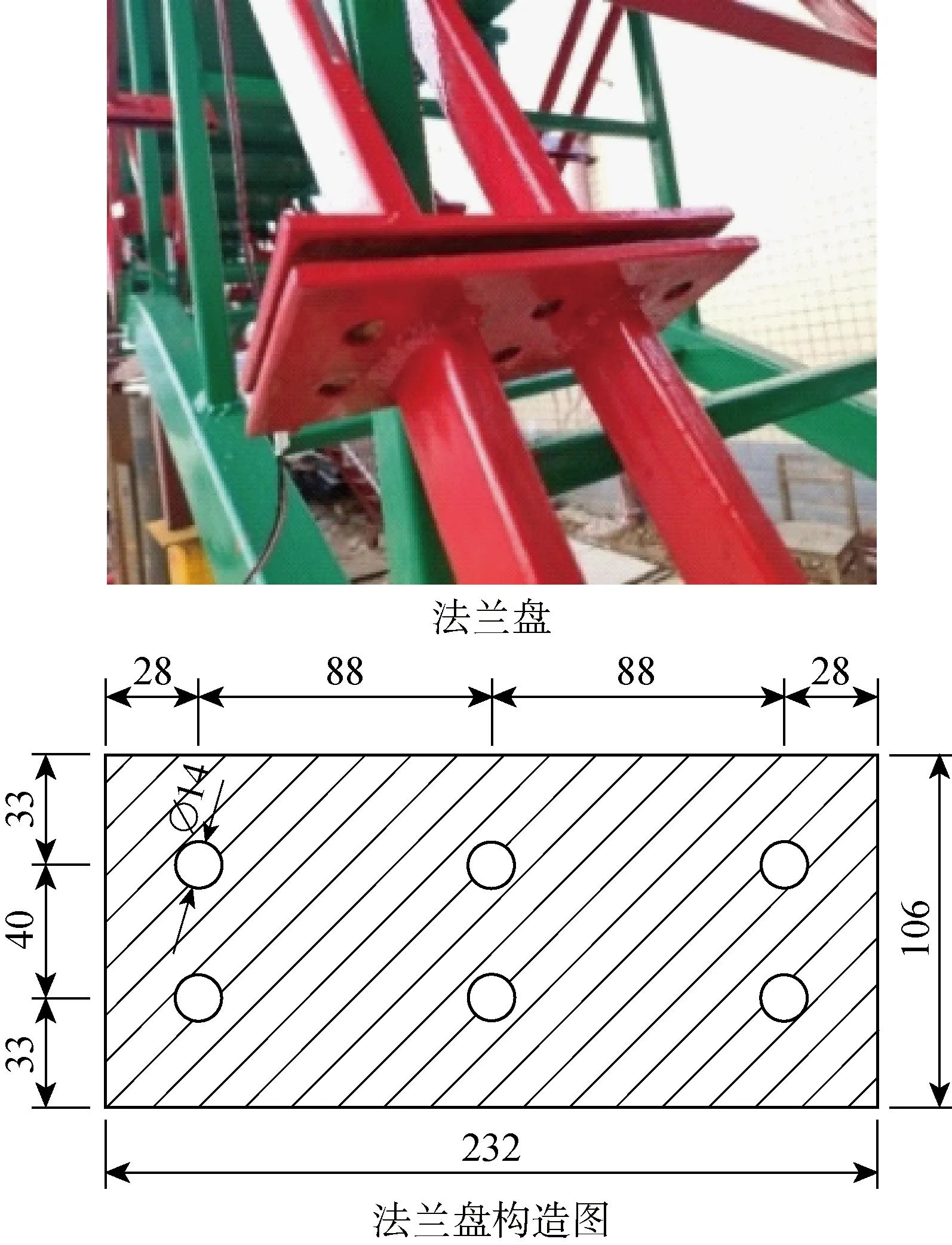
图8 法兰盘(mm)Fig.8 Flange (mm)

2.2 有限元计算结果

利用有限元计算软件Midas Civil建立试验桥的三维模型分析其自振频率及振型，现有上承式拱桥和上承式加V拱桥的有限元模型如图9所示，计算结果见表2，振型如图10和11所示.

图9 有限元模型Fig.9 Finite element model

图10 现有上承式拱桥振型Fig.10 Vibration modes of existing deck arch bridge

图11 上承式加V拱桥振型Fig.11 Vibration modes of deck V-arch bridge

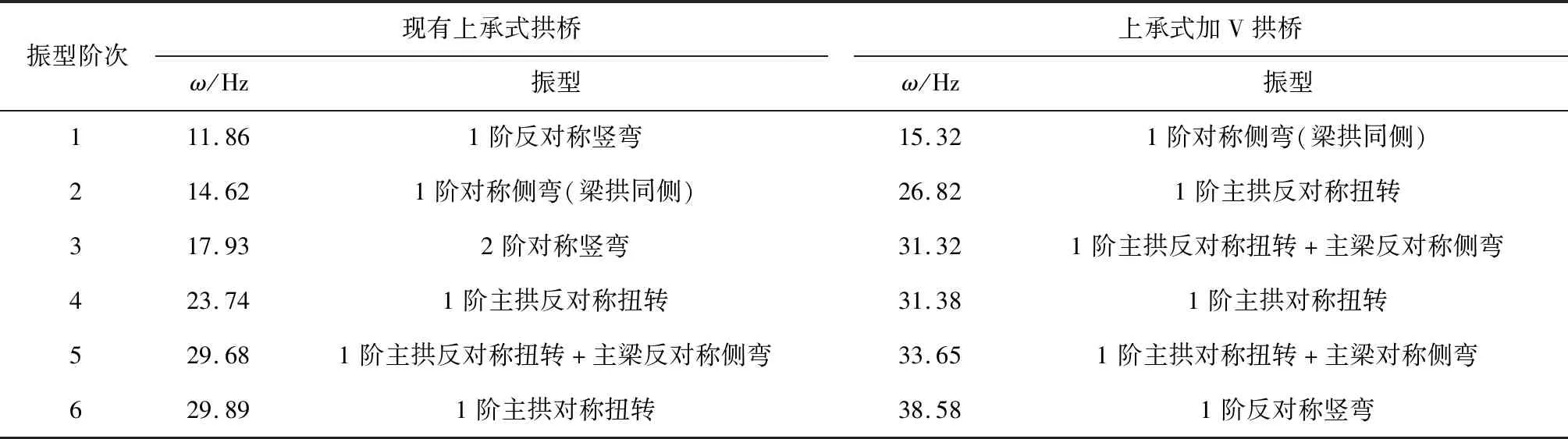
表2 计算模型前6阶自振频率及振型Tab.2 First 6th natural frequencies and vibration modes of calculation model

有限元软件分析结果表明，V形构件的增设不仅大大提高了上承式加V拱桥的面内刚度，扭转及面外刚度亦有不同程度的提高，故其振型特征与现有上承式拱桥存在较大差异，具体表现为面外侧弯、扭转振型提前，面内竖弯振型相对较少且出现的阶次较高.现有上承式拱桥的1阶振型为拱圈和主梁反对称竖弯，而上承式加V拱桥的1阶振型为梁拱对称侧弯.首次发生面内竖弯时，现有上承式拱桥的频率仅为11.86 Hz，而上承式加V拱桥的频率达到38.58 Hz，增幅高达225.30%.首次发生面外侧弯时，现有上承式拱桥的频率为14.62 Hz，上承式加V拱桥的频率为15.32 Hz，后者比前者提高4.79%.首次发生主拱反对称扭转时，现有上承式拱桥和上承式加V拱桥的自振频率分别为23.74 Hz和26.82 Hz，后者比前者提高12.97%.

由此可见，上承式加V拱桥的自振频率较现有上承式拱桥有较大幅度的提高，其面内自振频率提高的效果最为明显.

2.3 试验结果分析

脉动试验所用拾振器为2D001V磁电式速度传感器，测点共3个，沿桥梁中心线分别布置在L/4、L/2、3L/4处，测点布置及现场试验分别如图12和13所示，桥梁竖向加速度信号采集由DH5981动态信号采集仪完成.试验时现有上承式拱桥的采样频率为50 Hz，上承式加V拱桥的采样频率为100 Hz，现场采样时间不少于30 min.

图12 测点布置图Fig.12 Layout of measurement nodes

图13 现场试验Fig.13 The field test

脉动试验记录了试验桥振动速度时程曲线，对其进行频谱分析产生相应的频谱曲线.对应布置于L/4、L/2、3L/4桥跨截面处测点频谱曲线如图14所示.图中ζ为阻尼比.图15为试验所测得的振型图，图中a为加速度.表3给出了首次发生面内竖弯时自振频率的试验值和计算值.

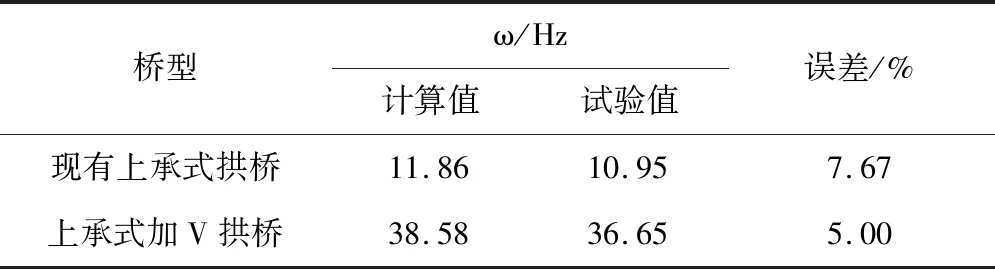
表3 首次发生面内竖弯自振频率的试验结果与计算结果Tab.3 Test and calculation results of first natural frequency of vertical bending in plane

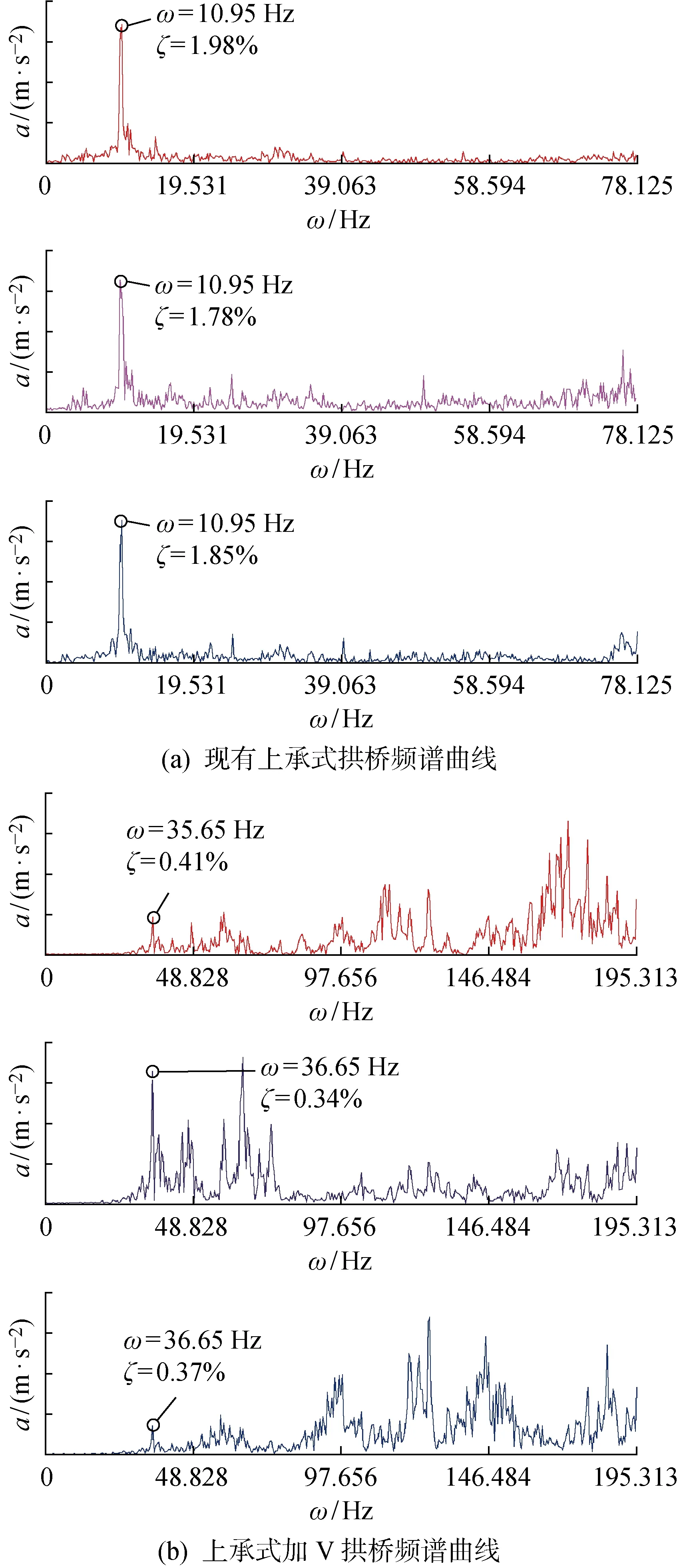
图14 频谱曲线Fig.14 Spectrum curves

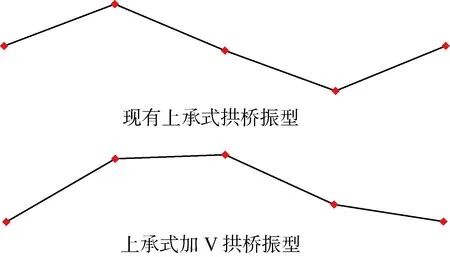
图15 振型Fig.15 Vibration mode

由试验结果可知，现有上承式拱桥首次发生面内竖弯的自振频率试验值为10.95 Hz，上承式加V拱桥首次发生面内竖弯的自振频率试验值为36.65 Hz，后者比前者提高234.70%，两者的试验值与有限元计算值相差较小，误差分别为7.67%和5.00%，两者的振型与有限元分析相吻合.现有上承式拱桥的ζ约为2%，而上承式加V拱桥的ζ较小，仅约为0.4%，这是由于增设V形构件后，上承式加V拱桥的主梁及拱圈的线刚度增大，故结构的整体刚度得到提高，且其质量较现有上承式拱桥要大.通过进行脉动试验，验证了上承式加V拱桥动力特性研究的正确性.

3 上承式加V拱桥有限元分析

为进一步验证上承式加V拱桥提高自振频率的有效性，以双线高速铁路拱桥为例，利用有限元软件建立三维模型分析上承式加V拱桥的动力特性和刚度，并与现有上承式拱桥进行对比，研究V形构件刚度对结构动力特性以及V形构件数量对结构温度应力的影响，并对结构体系转换的有效性进行验证.

3.1 结构布置

现有上承式拱桥和上承式加V拱桥拱圈截面如图16所示.通过调整钢箱型拱圈的截面尺寸，保证用钢量相同(约为1.4万吨).表4给出了其余构件的参数及材料具体用量.以跨径为450 m的双线高速铁路拱桥为例，矢跨比为1/5，拱轴线采用悬链线，拱轴系数为2.7，桥面总宽为20 m，结构布置如图17所示.

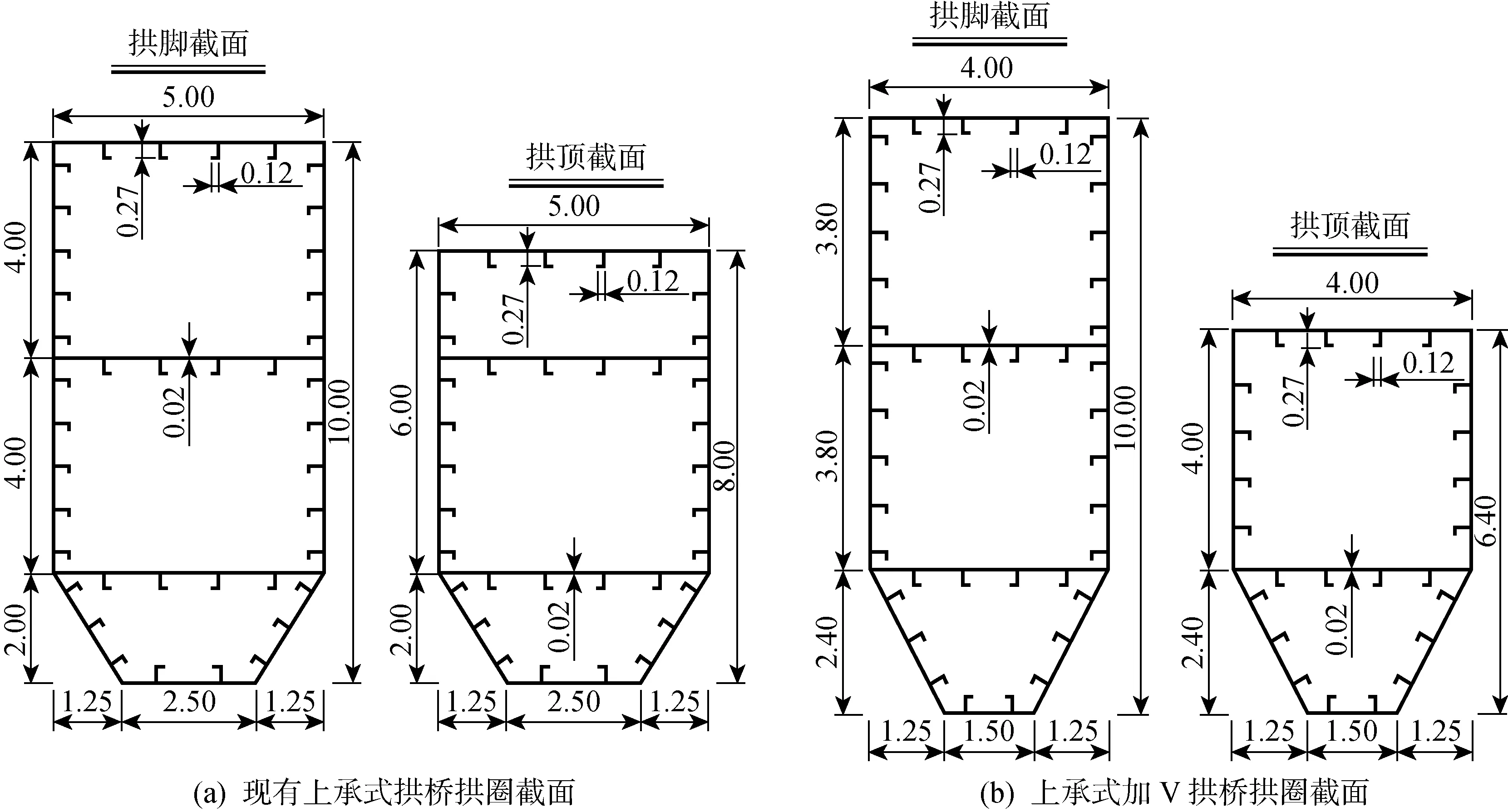
图16 拱圈截面(m)Fig.16 Section of arch ribs (m)

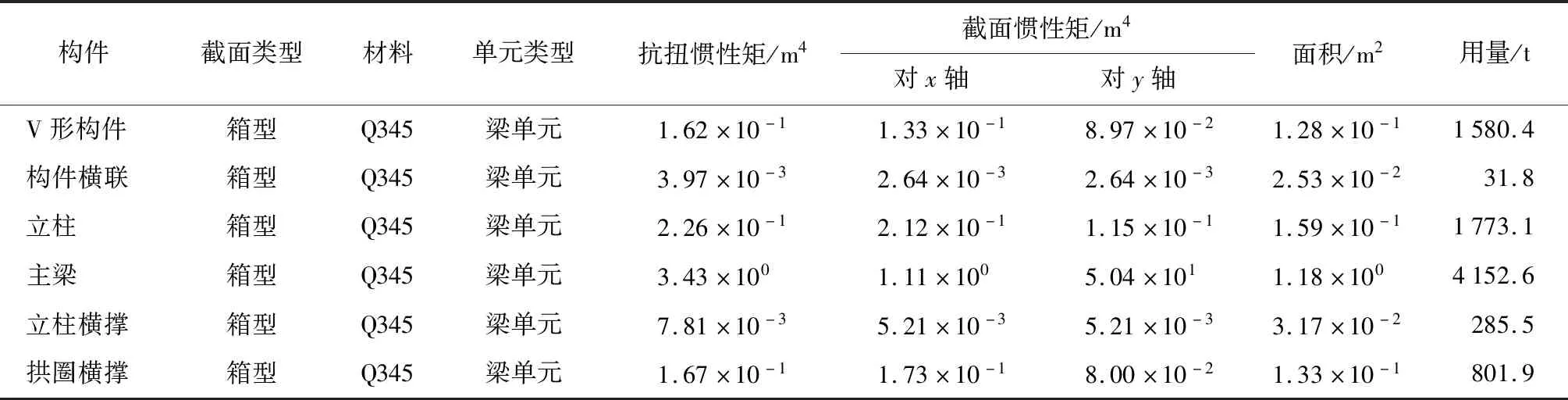
表4 构件参数及材料用量表Tab.4 Parameters and amount of members

图17 450 m上承式加V拱桥结构布置图(m)Fig.17 Layout of deck V-arch bridge with a span of 450 m (m)

3.2 结构动力特性有限元分析

有限元软件的分析结果表明，尽管用钢量相同，但是在同一振型阶次下，上承式加V拱桥的自振频率较现有上承式拱桥仍有较为明显的增幅.具体到同一振型特征下时，通过计算可以发现，上承式加V拱桥首次发生面外侧弯、反对称扭转、面内竖弯的自振频率分别比现有上承式拱桥提高了8.56%、8.56%以及89.84%，增量较为可观.限于篇幅，以下仅给出模型的前5阶自振频率以及振型，具体结果见表5.

表5 计算模型前5阶自振频率及振型Tab.5 First 5th natural frequencies and vibration modes of calculation model

综上可知，即使在用钢量相同的情况下，上承式加V拱桥的自振频率较现有上承式拱桥仍有较大幅的提高，因此，该种桥型不仅动力性能优越，且经济性较好，在方案比选时具备较强的竞争力.

3.3 V形构件刚度对结构动力特性的影响

V形构件作为新增构件，其刚度对上承式加V拱桥的整体刚度有着重要影响，会影响其自振频率和振型.在第3.1节450 m双线高速铁路拱桥模型中所用V形构件的基础上，采用保持壁厚不变改变截面尺寸的方式实现V形构件的刚度变化，截面尺寸依次为1.3 m×1.0 m、1.8 m×1.5 m、2.0 m×1.8 m、2.6 m×2.0 m、3.0 m×2.5 m、3.6 m×3.0 m、4.5 m×3.5 m、5.0 m×4.8 m，将上承式加V拱桥首次出现面外侧弯、面内竖弯的自振频率进行比较，具体结果见表6.

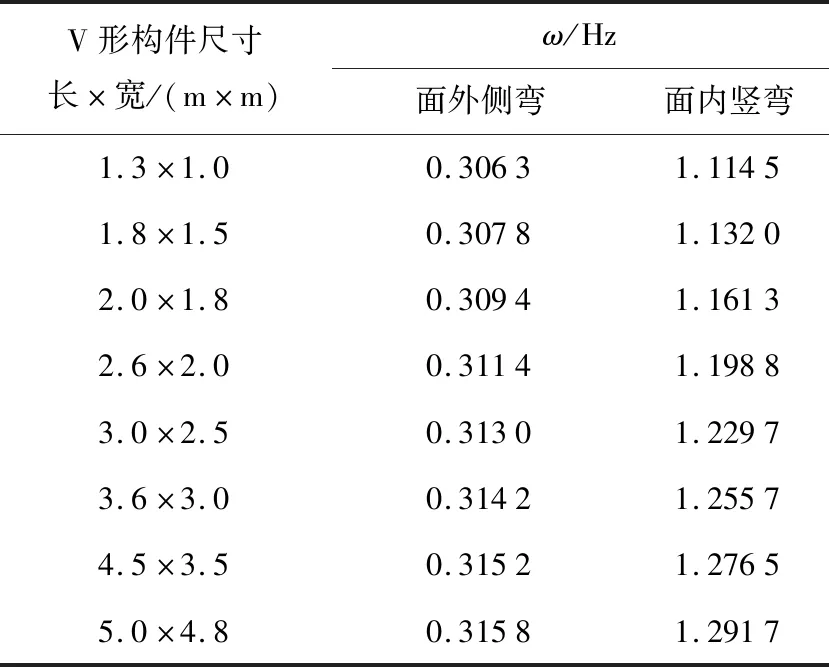
表6 V形构件刚度变化时上承式加V拱桥首次发生面内及面外的自振频率Tab.6 First in-plane and out-of-plane natural frequencies of deck V-arch bridge when stiffness of V-shaped members changes

随着V形构件刚度的不断增加，上承式加V拱桥首次发生面外侧弯的自振频率略有提高，但是增量较小.首次发生面内竖弯的自振频率亦随V形构件刚度的增加而提高，增幅虽较面外侧弯明显，但是增量较为有限.研究中所设V形构件的最小尺寸为1.3 m×1.0 m，当尺寸增大到5.0 m×4.8 m时，V形构件的用钢量占比由5.57%增至19.74%，首次发生面外侧弯的自振频率由0.306 3 Hz增大到0.315 8 Hz，增幅仅为3.10%.首次发生面内竖弯的自振频率由 1.114 5 Hz增大到 1.291 7 Hz，增幅为15.90%.另外，通过比较面内竖弯自振频率曲线的斜率变化可知，当V形构件尺寸的变化范围在1.8 m×1.5 m到3.0 m×2.5 m时，自振频率的增幅最为明显，这两种尺寸下V形构件的用钢量占比分别为7.74%和12.18%.可见，V形构件的刚度存在一个合理的设置范围，经计算，V型构件、主梁(L)和拱圈(G)的抗弯刚度之比EIV∶EIL∶EIG=0.035 3∶50.4∶5.35～0.165∶50.4∶5.35，抗压刚度之比EAV∶EAL∶EAG=0.091 6∶1.18∶0.877～0.153∶1.18∶0.877，此时，V形构件质量占全桥用钢量的8%～12%左右.

综上可知，V形构件刚度增加后，上承式加V拱桥的面外和面内刚度均得到一定的提高，故其相应的自振频率亦有小幅增长.此外，通过增加V形构件的刚度来提高上承式加V拱桥自振频率效果并不明显，且刚度的增加是以牺牲经济性为代价的，因此在具体设计时V形构件的刚度应综合各方因素进行选取.

3.4 结构刚度有限元分析

上承式加V拱桥自振频率的提高关键在于结构整体刚度的大幅提高，为了验证理论的正确性，根据《铁路桥涵设计规范》(TB10002-2017)的要求，利用3.1节所建模型对结构在①列车活载+0.5×温度荷载，②0.63×列车活载+温度荷载，③列车活载3个荷载工况下进行刚度研究.其中，列车荷载为ZK活载，初始温度为15 ℃，升温最终温度为40 ℃，降温最终温度为 -2 ℃.

上承式加V拱桥与现有上承式拱桥主梁的挠度计算结果见表7，表中W′为L/4跨处主梁上下挠度(绝对值)之和，δ为挠度变化率，c为容许值.上承式加V拱桥主梁上挠位移包络图如图18所示，图中D为位移.主梁L/4处位移影响线如图19所示.

表7 主梁挠度计算结果Tab.7 Calculation results of main girder deflection

图18 主梁上挠位移包络图(mm)Fig.18 Envelope diagram of up deflection displacement of main girder (mm)

图19 主梁L/4处位移影响线Fig.19 Influence of displacement of L/4 on main girder

在工况①下，现有上承式拱桥Wmax为221.64 mm，上承式加V拱桥为119.88 mm，相比之下后者变形减少45.91%.在工况②下，两者Wmax分别为223.77 mm和149.66 mm，相比之下后者变形减少33.12%.在工况③下，两者Wmax分别为164.20 mm和65.76 mm，相比之下后者变形减少59.95%.此外，在工况③下，W′为258.29 mm，而上承式加V拱桥的主梁不存在上挠，且其主梁上挠位移包络图中上挠值几乎为0，主梁L/4处位移影响线正面积几乎为0，共同说明了上承式加V拱桥克服了现有拱桥结构体系的固有弊端，更利于列车高速平稳行驶.

综上可知，在同等用钢量的情况下，上承式加V拱桥主梁位移值较现有上承式拱桥大幅减少，且结构不存在上挠现象.由此可见，上承式加V拱桥的刚度远大于现有上承式拱桥，因而可有效提高结构的自振频率.

3.5 V形构件数量对温度应力的影响分析

V形构件的数量决定着结构的超静定次数，故而会对结构的温度应力造成影响.为对V形构件的数量进行科学选取，在3.4节所建模型及其温度设置的基础上，将V形构件数量分别设置为3、5、7、9、11，计算结构在温度作用下的最大应力σmax，具体结果见表8，表中ω0为V型拱桥的基频.

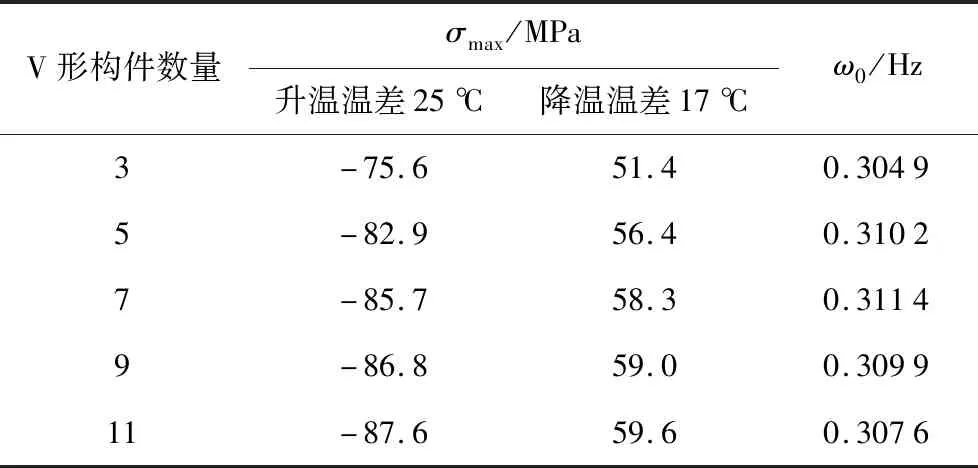
表8 V形构件数量变化时温度作用下上承式加V拱桥的最大应力Tab.8 Maximum stress of deck V-arch bridge under effect of temperature when number of V-shaped members changes

随着V形构件数量的不断增加，上承式加V拱桥在温度作用下σmax亦随之增大，且降温对σmax的影响大于升温；而V形构件数量增加时，上承式加V拱桥的ω0先增大后减小.当V形构件数量由3增加到11时，升温作用下σmax由 -75.6 MPa增加到 -87.6 MPa，增幅达15.87%；降温作用下σmax由51.4 MPa增加到59.6 MPa，增幅达15.95%.V形构件数量分别为7、9、11时，σmax因温度作用发生的变化较小，但是个数为7时，上承式加V拱桥的ω0达到最大值 0.311 4 Hz，V形构件的用钢量占全桥用钢量的比例为10.42%，而个数为11时用钢量占比达13.43%.

综上可知，当V形构件个数为7时，上承式加V拱桥的基频可达到最大值，而结构的最大温度应力不大，V形构件的用钢量亦较为合理.此时V形构件与主梁或拱圈所构成的三角形的内角在45°～60°之间，因此，控制好V形构件的个数，不仅可使结构的温度应力较小，亦可在保证经济性的前提下有效提高结构的基频.

3.6 V形构件加入的时间不同时拱圈受力分析

V形构件加入的时机对实现拱和桁架分阶段工作的目标，充分发挥拱受力的优越性至关重要.为研究V形构件加入的时间对拱结构受力的影响，利用3.1节所建模型分两例计算拱圈在最不利荷载组合作用下的应力.其中一例为一次成桥，即拱圈、主梁和V形构件同时施工.另一例为按现有上承式拱桥体系成桥后，加入V形构件，二次成桥完成体系转换，然后再上二期恒载，最终成桥.

上承式加V拱桥一次成桥和经过体系转换后二次成桥的拱圈压应力σ′如图20和21所示.

图20 一次成桥时拱圈压应力云图Fig.20 Compressive stress nephogram of arch ribs during one-time bridge construction

图21 二次成桥完成体系转换时拱圈压应力云图Fig.21 Compressive stress nephogram of arch ribs at completion of system conversion after secondary bridge formation

按一次成桥时，上承式加V拱桥的拱圈在最不利荷载组合作用下最大压应力为 -78.07 MPa，而经过体系转换后二次成桥时拱圈的最大压应力达到 -147.02 MPa，后者几乎为前者的两倍.

综上可知，V形构件加入的时机对上承式加V拱桥拱圈的受力有着很大影响，经过体系转换后二次成桥可充分发挥拱受力的优越性，故可有效利用主拱截面的材料强度，增强跨越能力.

4 结论

提出了一种新的拱桥结构体系，在理论研究的基础上，通过修建试验桥进行脉动试验，并利用有限元软件计算，验证了上承式加V拱桥动力特性的优越性，主要结论有：

(1) 上承式加V拱桥动力特性改善明显，其中以面内自振频率提高的效果最为显著.上承式加V拱桥及现有上承式拱桥首次发生面内竖弯的自振频率试验值分别为36.65 Hz和10.95 Hz，前者比后者提高234.70%，试验值与有限元软件计算值相差较小，试验误差分别为5.00%和7.67%，结构的振型与有限元分析相吻合.

(2) 上承式加V拱桥首次发生面外侧弯和面内竖弯的自振频率随V形构件刚度的增加而有小幅增长.V形构件的刚度设置存在1个合理的范围，其用量占全桥用钢量在8%～12%左右为宜.上承式加V拱桥的基频随V形构件数量的增加先增大后减小，其个数应以能使其与主梁或拱圈所构成的三角形的内角在45°～60°之间为宜.

(3) 跨径为450 m的双线高速铁路上承式加V拱桥有限元分析表明，结构刚度大幅提高.V形构件有效提高了结构的整体刚度.在列车活载作用下，由V形构件与拱圈及主梁节段所形成的三角形参与抵抗变形，主梁位移值较现有上承式拱桥大幅减少，且结构不存在上挠现象.此外，上承式加V拱桥经过体系转换后二次成桥的成桥方法可充分发挥拱受力的优越性，有利于进一步增强跨越能力.

综上所述，上承式加V拱桥的动力特性较好，且其刚度较现有上承式拱桥有较大幅度的提高，考虑到其良好的力学特性和经济性，可尽早应用于重载及高速铁路桥梁的建设.