基于图限制合作博弈有效分配原则的医疗联合体利益分配机制

蔡 蕾,史纪磊,李 理,单而芳

(1.上海大学 管理学院,上海 200444;2.上海市第一人民医院,上海 200080)

医疗联合体(简称医联体)又称为医疗共同体或医疗集团[1],是不同层级、类别的医疗卫生机构通过纵向或横向的资源整合所形成的医疗机构联合组织。宏观上,其建立的目的是为了缓解我国卫生资源配置的结构性矛盾,降低医疗成本,提高资源利用率和综合医疗技术水平。微观上,组建医联体是不同医疗机构在市场竞争的刺激下通过优势互补,提高竞争力、谋求生存发展的必然途径,需要充分考虑各自的地域分布、功能定位、服务能力、业务关系以及合作意愿等。

医联体的组织形式包括:城市医疗集团、县域医疗共同体、跨区域专科联盟、远程医疗协作网、城乡对口帮扶、托管、技术协作等[2]。截至目前,我国各地区大多采取以三级综合性医院为核心,联合区域内的专科医院、二级医院和基层医疗机构组成区域医联体,以期达到管理科学、功能齐全、服务完善、资源配置合理的目标。其中,部分具有技术、人才、管理和服务优势的大型医院采取了资产重组、合并、兼并、合作以及合资等形式,组成医疗集团,实施经营管理理念推广和医疗技术渗透。

1 相关研究评述

近年来,部分国内外学者探讨了医联体相关效用的分配办法。李忠萍等[3]运用排队与博弈论,构建了从综合医院到社区医疗服务中心转诊的期望效益函数模型,研究了有效刺激综合医院将病人下转的支付策略。胡正东等[4]运用Shapley值法计算出医联体利益模型的利益分配比例,并在此基础上进行激励规划设计。王海燕等[5]利用最优化理论建立了信息共享平台运营商收益最大化模型,分析了各三级医院和各社区医院对于是否参与信息共享及参与信息共享后的付费所采取的策略。Li等[6]为医疗机构的反向转诊流程制定了可分析的排队模型,通过马尔科夫链过程分析患者群体动态,并进行了仿真实验。孙自学等[7]运用系统动力学方法模拟了不同条件下社区首诊率、双向转诊率变化情况。顾华[8]基于对医院关系和医患关系的博弈研究,构建了重大疾病诊疗及康复全过程的医联体利益共享服务模式,并探索采用云计算技术来支撑医联体间的信息共享。Pan等[9]讨论了加强中国医院市场内部竞争的政策选择。Liu等[10]针对城市医院与基层医疗服务机构组成的医联体内部双向转诊问题建立了模型。张利江等[11]针对区域医联体中的协同医疗任务分配问题,借助模糊数学中的隶属度理论,以患者满意度为目标函数,在符合临床路径标准的时间、成本、质量约束下建立0～1整数规划模型。Allard等[12]对全科医师共同支付机制的一些激励性质进行了分析和比较。

上述文献大多围绕医院的转诊任务或转诊人数展开研究。主要采用函数分析法,在考虑某个目标函数最大或最小化的基础上,构建期望效益函数,继而计算出医联体成员间的最优转诊任务数或最优转诊人数。然而,文献中鲜少讨论影响和制约医联体发展的经济利益分配问题,如最佳转诊策略的公益性和经济性的二维问题、医联体成员间的公平分配问题以及成员间公平收益实现的预测问题等。

经济利益分配不公平是制约我国医联体发展的瓶颈,也影响了医联体的可持续性发展。本文基于图限制合作博弈的有效分配原则,对医联体整体增量经济利益的内部分配机制进行了研究。试用合作博弈理论建模,设计具有可操作性的经济收益的分配方案,为解决医联体“联而不通”的问题做出一定贡献。

2 问题描述

2.1 医联体的疾病诊疗效用

医联体的疾病诊疗效用是指组建医联体用于改善居民的健康水平所达到的程度[13]。医联体成员间的相互转诊是实现该效用的重要手段和主要方法,医联体对内部不同层级医疗机构之间的诊疗人数进行合理配置,可以引导居民就近、合理就医,从而提高资源利用率,缓解卫生资源配置的结构性矛盾。转诊的标的是转诊人数(次),目的是基于医联体内部各医疗机构所能胜任的病种难度指数,在时间、资源、质量等约束条件下,通过成员间的相互转诊,获得医联体整体最大的疾病诊治效用。

首先,设计一个简单的模型:某医联体由一所社区医院和一所三级医院组成。任何疾病品种(简称病种)在这个医联体内均能够获得两种诊治服务:高技术水平服务(H)和低技术水平服务(L)。其中,三级医院不仅能够提供L 服务,也能提供H 服务;但社区医院仅能提供L服务。用q表示疾病诊疗的边际效用,s表示病种组合难度。设高技术水平的诊疗服务所能取得的效用与病人的病种难度成正比,而低技术水平的诊疗服务无论病种难度如何,所能获得的效用恒定不变,用a、b分别表示医联体提供的诊疗服务效用与病种难度的正比例系数,则:

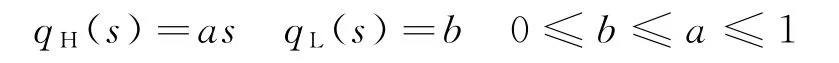
用一个二元组Q(ni,αi)表示这个医联体的疾病诊疗总效用。其中:ni表示病人个体;αi表示单位个体的病种难度。医联体的病种组合难度系数之和为1,医联体所能承担的病种组合难度系数为si,si∈[αi-1/2,αi+1/2],且αi≥1/2。

根据诊疗服务效用与病种难度的比例关系,医联体接诊的病种难度只有在超过既定的病种难度时,采用高技术水平的诊疗服务才能获得边际效用。设这个既定的病种难度为～si,则超过既定难度的病人个体可表示为:ni≡αi+1/2-～si。医联体的疾病诊疗效用可表示为

由上式可知,病种组合难度超过既定水平,即(αi+1/2)＞ni时,使用H诊疗服务,获得的效用才会随接诊人数的增加而递增。当a=1,b=0时,疾病诊疗效用最大为:。

要使医联体的整体疾病诊疗效用最大化,应尽量使病种难度较高的病人分配到H,病种难度较低的病人分配到L。此外,社区医院接诊不能超越自身的最大病种难度接诊水平。可见,医联体各成员最重要的效用分配任务就是根据病种难度进行上下转诊,使病种难度较高的病人尽快获得H 诊疗服务。

2.2 医联体成员转诊的瓶颈

但在实际运作中发现,很多医联体建设处于“联而不通、动而乏力”“叫好不叫座”的困境,转诊制度的实施面临诸多困难。上海市人民政府决策咨询专项课题组[14]在2014 年1～9月对15名专家展开咨询,将制约上海医疗联合体顺利推进的主要因素在准则层归结为政策、利益、管理和患者需求4 个方面。发现在对目标层权重贡献度最高的8 个要素中,有7个都与利益层有关。利益因素已经成为决定上海市医联体能否顺利推进的核心要素。

以一家三级医院和一家社区医院组成的最简单的医联体模型为例,假设在按病种付费(DRGs1)指根据病人的年龄、性别、住院天数、临床诊断、病症、手术以及疾病严重程度,合并症与并发症及转归等因素把病人分入500～600个诊断相关组,然后决定应该给医院多少补偿。是当今世界公认的比较先进的支付方式之一)的模式下,社区医院和三级医院的收费标准相同。社区医院收治病种难度低的病人的边际净收益为VL,收治病种难度高的病人的边际净收益为VH。社区医院上转或三级医院下转病人时面临的机会成本分别为COL和COH,社区医院每例误诊费用为Cm(此处设误诊仅仅出现在社区医院收治病种难度超过自身接诊能力的情况下,三级医院没有误诊)。医联体单位时间内的接诊人数为λ。医联体的总体接诊阈值为1,社区医院的最优接诊阈值为k1,三级医院的最优接诊阈值为1-k1。社区医院单位时间上转病人率(单位时间内向三级医院的转诊人数)为λ1-2,三级医院单位时间下转病人率(单位时间内向社区医院的转诊人数)为λ2-1,两类医疗机构单位时间内满足疾病诊疗效用最大化的最优收治人数分别为λ11和λ22。则社区医院和三级医院单位时间的最优收治人数分别为:

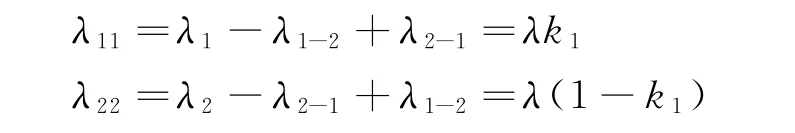
在医联体成员按照各自的最优转诊阈值K1,1-K1互相转诊的前提下,社区医院面临的平均机会成本为:COL=λ1-2(VL-Cm),三级医院面临的平均机会成本为:COH=λ2-1VH。两种医院面临的平均机会成本基本不相等:在大多数情况下,VH远大于VL,三级医院需要承担更多机会成本。出于经济利益的考虑,三级医院必然不希望将可以带来较多经济收益的病人转给社区医院,医联体“转上容易转下难”。

3 图限制合作博弈分配原则对医联体的适用性

1944年,冯·诺伊曼和摩根斯坦具有里程碑意义的著作[15]的出版,正式宣告了博弈论的诞生。合作博弈论是博弈论的分支,强调集体理性,即通常所说的“双赢”或“多赢”。一个合作博弈可以记为(N,v),向量x=(x1,x2,…,xn)为其分配方案。其中,xi为参与者i∈N所得的份额。当=v(N),称x满足有效性;当xi≥v(i),∀i∈N,称x满足个体理性;当≥v(S),∀S⊆N,称x满足群体理性。满足上述3种性质的分配方案组成的集合称为该博弈的核心,记为

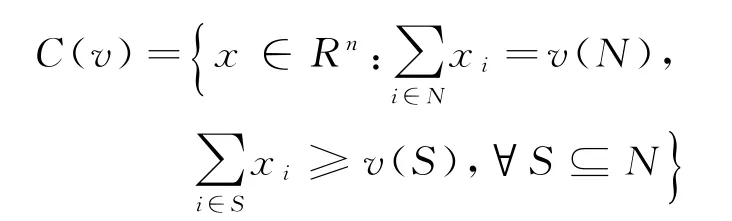
医联体成立的目的是为了激励每位成员对所在联盟的边际贡献随着联盟规模的扩大而增加,表示为:对于任意S,T∈2N,有

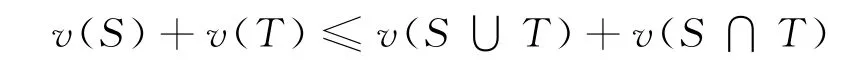
此外,要求任何两名或两名以上成员间合作所带来的收益要超过成员单独运营所产生收益的和,表示为:对于任意S,T∈2N且S∩T=φ,有v(S)+v(T)≤v(S∪T)。

医联体的构成比较复杂,成员不仅包括三级医院和社区医院,还可能包括二级医院、民营医院、康复中心和检验中心等其他医疗机构。以一个由一所三级医院(成员1)、一所二级医院(成员2)和两所社区医院(成员3、4)组成的医联体为例,可以存在多种结构,如图1～4 所示。

图1 完全连通联盟结构

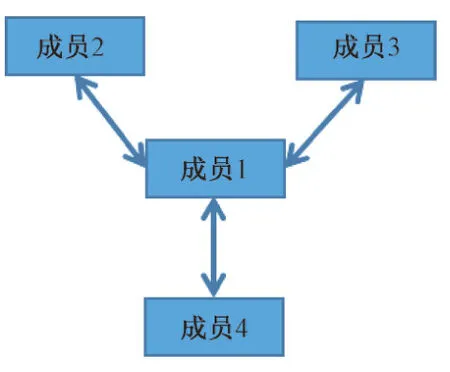
图2 星型联盟结构

图3 树型联盟结构

图4 部分成员不连通结构

图1为完全连通联盟结构,即每个医联体成员彼此之间都可以相互转诊。图2为星形联盟结构,即以三级医院为中心,分别连通医联体中的二级医院和社区医院,但除该中心之外的其他成员之间彼此不连通。图3 为树形联盟结构,即医联体“根”-“枝”-“叶”的方式进行连通,三级医院是树形结构中的“根”,社区医院全部都为“叶子”。图4为非完全连通结构,表示部分成员之间未建立转诊关系。

鉴于医联体合作基于各成员之间关于权利义务的“契约”约定,且不同医联体的组成结构各不相同。因此,医联体本质上是具有图限制结构的合作博弈。

关于合作博弈的求解问题,有如下几种基本算法:

(1)使用Shapley[16]公式可计算出Shapley值Φi(N,v),表示对于一个由N名参与者组成的合作博弈(N,v),参与者i∈N所得的份额为

Shapley值也可以由Harsanyi[17]红利公式表示为

式中,参数λS(v)称为一致系数。

(2)Myerson[18]通过(N,vL)表示由特征函数v引导的图限制合作博弈,其特征函数为

Myerson 值被定义为图限制博弈(N,vL)的Shapley值,记为μ(N,v,L),即对任意i∈N,

(3)为了强调图限制合作博弈中边的交流作用,Meessen[19]和Borm 等[20]进一步引入了边博弈(L,rv)的概念,在Myerson 值的基础上提出了Position值[21],即对任意i∈N,有

(4)Calvo等[22]进一步深化研究,认为在图限制合作博弈(N,v,L)中任意连通的两个成员不一定能百分之百达到合作,他对任意两个成员之间赋予一个概率

表示他们之间直接连通的可能性,进一步定义了概率图博弈(N,v,p),即对于任意的L⊆LN,图L实现的概率为

(5)Ghintran等[23]和Gomez等[24]定义了概率图L上的Position值,即对任意的i∈N,有

如果以医联体整体技术水平提高对各成员带来的好处(即医联体增量经济收益)为分配标的,则其分配方案为一个n维向量x=(x1,x2,…,xn),其中,xi为对第i个成员的分配。鉴于日常工作获取数据手段的限制,增量经济收益可根据“组成任何小联盟的成员年度业务收入扣除直接成本的增加值(相对于不加入联盟取得的收入)的合计数—转诊产生的机会成本的合计数”的会计公式进行核算,基于单位的财务会计记录获取医联体合作博弈的特征函数。

通过图限制合作博弈的方法计算分配金额,可以保证:

(1)x是一个有效分配,=v(S),即所有医联体小联盟的增量收益在成员中能够全部分配完毕。

(2)每位成员的收益满足xi≥v({i}),即成员加入医联体所能获得的分配不少于其单独运营所获得的经济收益增量。

可见,使用图限制合作博弈的分配原则,可以保证医联体的稳定性及可持续发展。

4 算例分析

4.1 Shapley值法算例

某三级医院(成员1)、二级医院(成员2)和社区医院(成员3)于2019年初组成医联体(N,v),N={1,2,3}。医联体结构如图5所示。

图5 某医联体结构

2019 年度,三级医院向二级医院下转病人1 500人次,向社区医院下转病人1 000人次(如果不下转,这部分人群将给三级医院带来收益4 500万元)。二级医院向社区医院下转病人500人次(如果不下转,这部分人群将给二级医院带来收益600万元),向三级医院上转病人200人次(如果不上转,这部分人群将给二级医院带来收益200万元)。社区医院同期向二级医院上转病人500人次,向三级医院上转病人300人次(如果不上转,这部分人群将给社区医院带来收益1 320万元)。

2018和2019年度,三级医院的业务收入(扣除直接成本)分别为28亿元和30亿元;二级医院的业务收入(扣除直接成本)分别为10亿元和11亿元;社区医院的业务收入(扣除直接成本)分别为1亿元和1.45亿元。

成员自由搭配建立各个子联盟所能获取的边际收益分别为(单位:亿元):

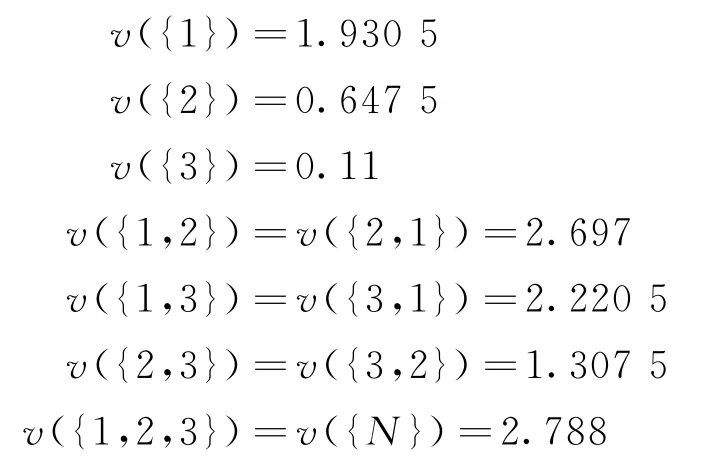
上述数据表明,三级、二级和社区医院如果单独运营,2019年度相对2018年度的收益增值分别为1.930 5、0.647 5和0.11亿元。如果三级和二级医院合作,则增值2.697亿元。如果三级医院和社区医院合作,则增值2.220 5亿元。如果二级医院和社区医院合作,则增值1.307 5亿元。如果三者合作,则增值可达2.788亿元。

用Shapley值法进行计算,对各成员的分配结果如表1所示。

表1 采用Shapley值法计算的分配结果 亿元

4.2 Myerson值法算例

某三级医院(成员1)、二级医院(成员2)和社区医院(成员 3、4)组成医联体(N,v,L),,医联体内实施分级诊疗(三级医院负责疑难危重症的诊治,二级医院负责较难病种的诊治,社区医院负责普通、慢性疾病的诊治及康复诊疗)。

医联体可能的结构设计分别见图1～4。设L为成员间互相转诊的关系,称为“边”,S为医联体内各成员组成的小联盟,v为医联体获得的增量经济收益。任何2名连通的成员合作,增量收益为60;任何3名连通的成员合作,增量收益为96;4名成员合作,增量经济收益为200。该医联体的特征函数为

用Myerson值法进行计算,根据图1～4的不同结构,分配结果如表2所示。

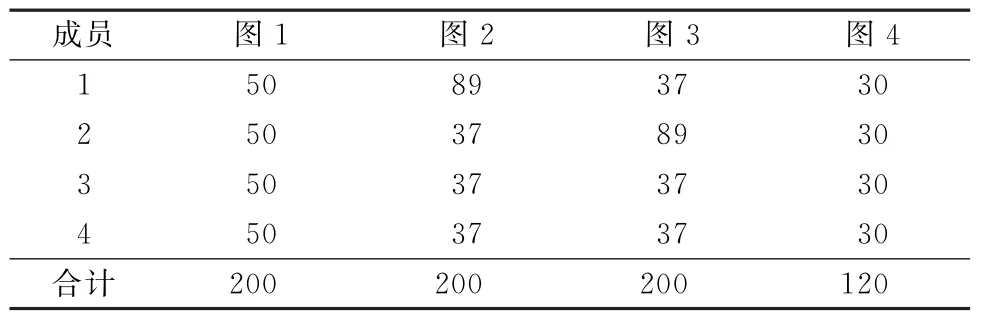
表2 采用Myerson值法计算的分配结果 万元

结果表明,除图4结构外,医联体增量经济收益在成员之中全部分配完毕。图4 结构存在两个分支,互相之间是不连通的。各成员分配到的经济收益合计为120万元,显然比4名成员组成一个连通结构分配到的要少。

4.3 Position值法算例

某三级医院(成员1)、二级医院(成员2)和社区医院(成员3、4、5)组成医联体(L,rv),L为医联体内相互转诊关系的集合,L={a,b,c,d},其中:a=12,b=23,c=24,d=15。rv为成员互相转诊所能带来的增量经济收益。医联体结构如图6所示。

图6 某医联体结构

该医联体的收益特征函数为

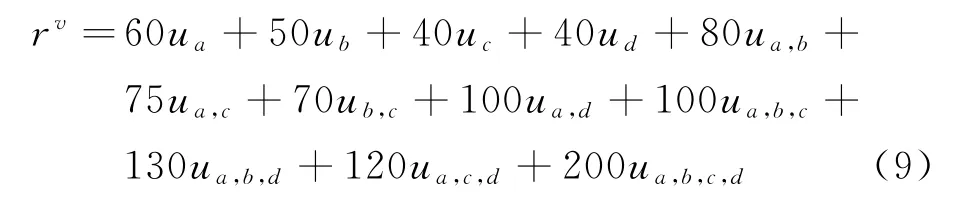
由式(5)可得分配结果,如表3所示。

表3 采用Position值法计算的分配结果 万元

Position值法强调对于关系的分配,实质是将医联体成员间的关系(边)视为“参与者”,首先使用Myerson值法进行分配,然后将每条边所分配到的收益平均分配给组成该边的两位成员。在本算例中,成员2在医联体中和其他成员建立的转诊关系最多,因此所获得的分配金额也最多。

5 基于概率图的分配预测

使用图限制合作博弈的方法进行医联体增量经济收益分配,必须考虑到医联体各边上转诊关系建立的可能性大小。在图6表示的算例中,进一步将病人通过医联体中每条边转诊的可能性表示为p,。可使用概率图合作博弈[18-20]方法,预测每位成员可以分配到的边际收益。

设p为医联体成员间转诊关系(边)建立的概率;=该边上可能的上转数/医联体达到最优接诊阈值时的上转数总体要求;其中,上转的可能性为,下转的可能性为=该边上可能的下转数/医联体达到最优接诊阈值时的下转数总体要求。

图6中,需上转的病人有80%的可能选择在社区医院首诊(选择成员3、4、5 的可能性分别为40%、20%和20%),20%的可能选择在二级医院首诊。社区医院将病人上转至二级医院后,其中可能有40%需要继续上转至三级医院,则:

需下转的病人中,有70%的可能选择三级医院首诊,30%的可能选择二级医院首诊。在选择三级医院首诊的病人中,下转成员2、5的可能性分别为50%和50%。三级医院下转至二级医院的病人中,有20%可能继续下转至社区医院。二级医院下转成员3、4的可能性分别为70%和30%。则:

鉴于每条边代表的关系是双向的,既存在上转,也存在下转,此处用的算术平均数计算各边组建的概率,如表4所示。

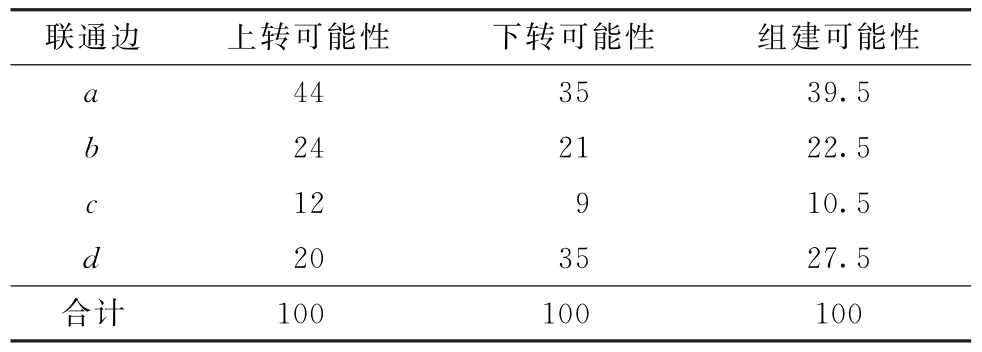
表4 各边组建的概率 %

结合式(6)、(7)进行计算,预测分配结果如表5所示。

成员1～5 预计可以分配到的收益分别为100.66、110.64、28.31、12.38和30.75万元。

概率图的算法可被运用于医联体组建后的经济收益分配预测中。

表5 采用概率图上的Position值法计算的预测分配结果 万元

6 结语

医联体成员在彼此转诊过程中各自面临不同的机会成本,在经济利益无法得到保障的情况下,双向转诊往往成为一句空话。即使根据疾病诊疗服务功能最大化模型计算出了成员间相互转诊的最优人数,在实际操作中也无法执行。

根据关系契约理论2)源自美国法理社会学家Macauly,他认为合作是契约签订各方的基本特征,契约实施依赖于对未来收益的预期,执行结果只能由签约各方事后观察到,契约条款事先详列的成本非常高或第三方无法实证,医联体成员间的转诊行为只能借助于正式契约以外的其他组织机制来进行激励和制约。因此,有关部门需要对医联体设计一个较为公平、合理、有效、且具备可操作性的经济利益分配方案。这个方案应同时关注医联体效用的二维性,既考虑到疾病诊疗服务功能的最大化,也考虑到医联体总体经济利益的最大化;既能够保障医联体成员按照实际诊疗水平进行接诊和转诊,又能以经济利益为杠杆,激励各医院努力提高综合技术水平,合理配置各项资源。

本文建议上级卫生主管部门设计组建一个具有权威性、中立性的管理机构具体负责计算医联体增量利益的分配。并根据计算结果,通过转移支付的方式将资金落实到位,如向有关成员收缴管理费,或支付补偿款等。管理机构的设置方案如下:

(1)成立差额拨款的事业单位,由区卫生健康委员会直接管辖。可将单位的基本运营经费纳入区级财政预算,其他经费通过向医联体收取管理费加以解决。该单位可以同时负责区域范围内所有医联体的管理、核算及分配。

(2)设置非独立机构或部门,由区卫生健康委员会所属部门直接管辖。区卫生健康委员会、区医保部门建立科学有效的合作管理模式。医联体的分配通过区卫健委有关部门进行核算,由医保部门在医保结算的同时进行转移支付。

(3)设置非独立机构或部门,挂靠在区域医联体牵头医院,接受区卫生健康委员会的业务指导,使绩效考核工作与效益分配工作结合起来,提高管理效率。机构的运营经费可通过向医联体内部各成员抽取一定管理费加以解决。

管理机构的设置方案确定以后,应保证医联体内每个成员都签订“目标责任书”或“管理协议”,从而使医联体的管理具备约束力,保证分级诊疗和效益分配得以有效执行。

合作博弈论是一门应用性很强的学科,很多概念和定理有重要的经济学意义[25-26],而且很多合作博弈论大师们的理论已经有广泛的现实应用。

本文后续研究的展望主要在应用研究方面,将从医联体运营的实践中寻到问题,为决策者提供理论依据,完成从理论到实际的飞跃。例如:从医联体组建的治理结构考虑图的结构问题;从医联体利益的函数性质考虑合作博弈的特征函数问题;从医联体组建的目标设计考虑图限制博弈的算法选择问题。此外,还要考虑数据的可取得性、算法的可操作性和信息化程度等。总之,将医联体理论研究与合作博弈理论相结合,将进一步提升医联体实践的科学性及合理性,有助于医联体的可持续发展。