基数约束投资组合选择问题

赵 磊,朱道立

(上海交通大学a.船舶海洋与建筑工程学院;b.安泰经济与管理学院;c.中美物流研究院,上海 200030)

投资组合指的是投资人或金融机构(投资银行、基金公司等)持有的股票、债券、金融衍生产品等组成的集合。投资人进行投资组合决策的主要目的是分散投资风险,在风险可控的前题下最大化投资收益。因此,在股票、债券等风险资产的投资中如何平衡收益和风险这两项指标进行资产分配是市场投资者迫切需要解决的问题,由此形成了投资组合理论和最优投资组合选择问题。

投资组合理论最早被Markowitz[1-2]提出。在这一理论中所求的投资组合方案由向量x表示,各项风险资产的投资回报率由向量ξ表示,理论假设向量ξ服从某一概率分布ω,同时这一概率分布的任意实现属于不确定集合

其中:Q∈Rn×n为半正定的协方差矩阵;μ∈Rn为期望收益。则投资组合方案的收益可由如下函数表示:ℓ(x,ξ)=xΤξ。

Markowitz用风险资产的期望收益μ来刻画收益,以风险资产的协方差矩阵Q来刻画风险,提出投资组合选择问题的均值-方差模型。在Markowitz的基础上,Sharpe[3]使用收益与风险的比例来度量收益与风险,称为夏普比率最大化问题,使模型更为简洁。

20世纪90年代之后,J.P.Morgan为代表的投资银行由于其银行业务风险的需要,对经典投资组合优化问题中的风险评估方法进行重新刻画,提出了风险价值模型(Value-at-Risk,VaR)。VaR 模型是一种借助概率论和数理统计的方法对风险进行量化和测度的模型,由于其在测量不同市场的不同风险时的简便性,在美国联邦储备银行、美国证券交易委员会、欧盟、巴塞尔银行监督委员会等国际知名金融机构得到了广泛应用。

但是VaR 模型也存在着不满足风险次可加性公理的缺陷,故Artzner等[4]提出了一致性风险测度概念,并将满足单调性、一次齐次性、平移不变性和次可加性4条公理的风险测度定义为一致性风险测度。另一方面,Rockafellar等[5-6]将VaR 模型拓展为条件风险价值(Conditional Value-at-Risk,CVaR)模型,CVaR 模型是一种能保持凸性的一致性风险测度模型。

1 投资组合选择问题的数学模型

通常,投资组合选择问题被刻画为如下带耦合约束的非线性规划模型(P0):

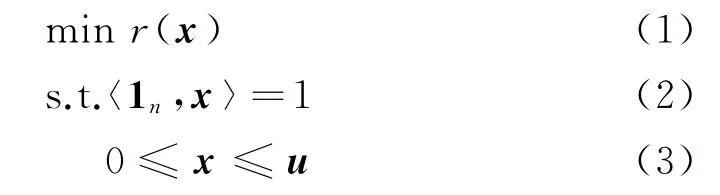
式中:1n为各元素均为1的n维向量;〈·,·〉表示Rn空间中两向量的内积。

这里考虑市场上的n个有风险的金融资产。投资者面临的决策是对这些金融资产进行投资组合选择,选择决策由变量x=(x1,x2,…,xn)Τ∈Rn表示,x的每一个元素xi,i=1,2,…,n表示对第i个资产的投入比例。本文中假设不允许卖空,因此,有x≥0;假设x存在上界u,u≥0。如果现实需求中没有明确给出上界u,通过预算约束式(2)不难得到u=1n。

文献中对于风险函数r(x)有多种刻画方式,下面介绍3种常见形式:

(1)均值方差形式[1,7]。Markowitz[1]以xTQx来衡量风险,因此可得当r(x)为下式时均值-方差模型[7-8](Pa)为

这一形式由Markowitz提出的投资组合理论而来,至今仍有广泛地应用。

(2)风险价值形式[5,6,8-10]。20世纪90年代,以J.P.Morgan为代表的投资银行对经典投资组合优化问题中的风险评估方法进行重新刻画,风险价值模型(VaR)被提出。关于信任等级β和投资方案x的VaR 模型定义为

由于VaR 模型存在着不满足风险次可加性公理的缺陷,Artzner等[4]提出了一致性风险测度概念,并将满足单调性、一次齐次性、平移不变性和次可加性4条公理的风险测度定义为一致性风险测度。条件VaR 模型(CVaR)由Rockafellar等[5]提出。此外,Rockafellar等得到在α∈R 最小化如下辅助函数时,CVaR 和VaR 一致,即

因此,CVaR 可表示为

在ξ服从正态分布条件下,令φ和Φ分别为正态分布的概率密度函数和分布函数。Fabozzi等[8]在Rockaffellar等[5]基础上,将VaR 模型转化为

式中,ζβ=-Φ-1(1-β),β＞0.5。从而得到VaR投资组合模型(Pb)。

进一步,如取积分形式,

CVaR 模型可转换为

因此可得CVaR 投资组合模型(Pc)。

Branda等[9]在Fabozzi等[8]基础上得到了鲁棒VaR 模型,即

以及鲁棒CVaR 模型:

因此可得鲁棒VaR 投资组合模型(Pd)和鲁棒CVaR 投资组合模型(Pe)。

由此可得在问题(P0)对应的r(x)分别为式(1b)～(1e)时,P0对应的问题分别为VaR 投资组合选择问题(Pb)、CVaR 投资组合选择问题(Pc)、RVaR 投资组合选择问题(Pd)以及RCVaR 投资组合选择问题(Pe)。

(3)损失函数形式[7,11-12]。在ξ偏离正态分布条件下,De Miguel等[7]提出了一类以损失函数作为目标函数的投资组合模型(Pρ),这一类模型被认为具有更好的鲁棒性。其中为代表的是M-投资组合模型。该模型中定义的r(x)即最小化收益波动如下所示:

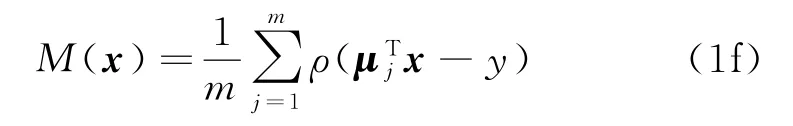
式中:ρ(·)是一个凸的损失函数;y为投资组合问题得到的收益。例如,经验轨迹误差函数[11]ρ1(ω)=‖ω‖2,投资组合规范函数[12]ρ2(ω)=log(1+ω)。

2 基数约束

近年来,投资者在进行投资组合选择时希望所得到的投资组合方案中被选择的资产数量可控。模型中通常以基数约束来刻画这一特征[13-19],即

式中:Card(x)均为向量x中非零元素的个数;τ为最多选择资产的个数。式(4)在通常状况下有如下两种等价数学表达。

(1)L0范数表达:

(2)混合整数约束表达:

式中:1n为各元素均为1的n维向量;〈·,·〉表示Rn空间中两向量的内积。

对于带L0范数约束问题的求解,目前文献中的研究主要分为两种:一是以L1范数替代L0范数的凸松弛方法[20-24]。但是,投资组合选择问题需要考虑的预算约束(式(2)),要求投资组合变量之和等于1,在不允许卖空情况下,又有x≥0。因此,投资组合变量的L1范数恒等于1。这一处理方法并不可行。另一研究方向为对L0范数约束问题进行近似,例如,以Lp范数(0＜p＜1)约束近似L0范数约束[25-28],以凹函数近似L0范数[9,29-30],以半正定规划问题近似带L0范数约束的投资组合优化问题[31]等,这一类方法通常运算效率很高,但理论结论往往不尽如人意,仅能得到局部最优解。

对于混合整数表达形式的求解,可利用经典混合整数规划方法,如分支定界法,以求得问题的全局最优解[17]。但是由于松弛下界问题求解困难,目前仅有文献[17]中利用混合整数约束研究带基数约束的均值-方差模型的全局最优求解方法。相关研究如表1所示。

表1 基数约束投资组合问题相关研究汇总表

本文研究一种应用广泛的基数约束投资组合模型。该模型以凸风险函数作为目标函数,在不允许卖空前题下,考虑基数约束和预算约束。带基数约束的投资组合优化中常见的均值-方差模型以及VaR、CVaR、RVaR 和RCVaR 模型等均是这一模型的特殊形式。

本文以混合整数形式刻画基数约束,将原问题刻画为非线性混合整数规划的形式。由于该模型下界松弛问题求解困难,目前尚无商用软件可以直接精确求解这一非线性混合整数规划模型。针对这个难点提出一种全局最优化算法,在分支定界法框架基础上,用有效的一阶算法求解下界松弛问题。最后,通过Fama-French(FF)产业投资组合基准测试数据集[32]中5、10、12 和17 等4组产业投资组合数据作为实验基础数据,设计仿真实验。实验结果表明,本文提出的方法能有效处理基数约束的产业投资组合问题,能够给出任意基数的投资组合方案。

3 问题描述与数学模型构建

定义:〈·,·〉表示Rn空间中两向量的内积;‖·‖p表示p阶范数,对

特别地,当p=0时,‖x‖0表示x中非零元素的个数;当p=∞时,。1n为各元素均为1的n维向量,0n为各元素均为0的n维向量,In为n维对角矩阵,On为n维0矩阵。⊙表示两向量对应元素相乘。

考虑如下基数约束投资组合模型(P):

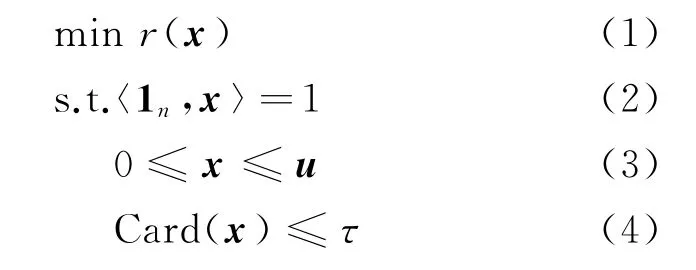
这里考虑市场上的n个有风险的金融资产。投资者面临的决策是对这些金融资产进行投资组合选择,选择决策由变量x∈Rn表示,x的每一个元素xi,i=1,2,…,n表示对第i个资产的投入比例。本文中假设不允许卖空,因此,有x≥0;假设x存在上界u,u≥0。如果现实需求中没有明确给出上界u,通过预算约束式(2)不难得到u=1n。此外,引入基数约束式(4),τ为最多投资的资产个数,则自然有1≤τ＜n。将风险函数式(1a)～(1f)统一为一个风险函数r(x),假设为光滑和凸的。

引入0-1变量构成的向量z∈{0,1}n,可将问题(P)写成如下混合整数规划问题(MIP):

不难看出,MIP是一个带耦合约束的不可分离非线性混合整数规划问题,由于其对应的连续松弛问题是一个带线性耦合约束的不可分离非线性规划问题,求解尤为困难,因而目前尚无可直接求解该问题全局最优解的商用软件。下一节将针对问题(MIP)进行求解算法的设计。本文将用分支定界法处理问题中的整数变量,并采用有效的一阶算法求解下界松弛问题。

4 算法设计

本节进行算法设计,应用一般分支定界算法框架设计算法[33]对问题(P)进行求解,以分支定界处理整数变量,以有效的一阶算法[34]求解松弛下界问题,它将在O(1/ε)的时间复杂度下得到下界松弛问题的ε近似最优解。

4.1 分支与松弛问题

本文算法中分支策略根据整数变量构成的向量z的取值进行,对应的分支树如图1所示。分支树上的每一节点都对应不同的向量z的取值。

由图1不难得出分支:

图1 分支树结构图

以此类推。

令l为一个包含nl个元素的0-1序列,nl≤n,对任意i满足1≤i≤nl,li为序列中第i个元素,任意

如果nl＜n,则对Sl进行分支,即将Sl0和Sl1加入分支列表。

定义分支Sl对应的松弛问题(RPl)为:

不难得出关于分支树的剪枝条件的命题1。

命题1分支树可以在如下3 种条件下进行剪枝:

(1)RPl无解。

(2)RPl的最优解满足≤τ。

证明

(1)说明当前分支无可行解。

(3)隐含了这一分支一定不是最优解。证毕

需要考虑到,RPl是一个带线性约束的不可分离的凸规划问题。这一问题的求解本身具有相当大的难度,本文将用一阶算法对其进行求解。这一问题的求解过程详见4.3节。

4.2 算法框架

根据4.1节中对分支、松弛问题的定义以及剪枝条件给出算法的总体框架,算法总体流程如下:

输入基数约束投资组合问题的所有参数。

输出所需投资组合方案。

步骤1初始化。设置分支集合。

步骤2终止条件检验。如果分支集合,则当前解为最优解,当前上界为最优值。

步骤3分支选择与松弛问题计算。从中选择Sl,并将Sl从中删除。求解其对应的松弛问题(RPl)。定义为RPl的最优值,为RPl的最优解。

步骤4剪支:

步骤5分支。令为Sl的分支,将这些分支加入,更新下界,j=1,2,…,k,返回步骤2。

4.3 松弛下界问题求解算法设计

本节给出松弛下界问题的求解算法,RPl为一个带耦合约束的凸非线性规划问题,该问题的求解本身具有相当大的难度,首先根据分支Sl对RPl进行等价转化。

由RPl中式(8)～(10)不难得到,在当前分支Sl中,∀i=1,2,…,n,当zi=0时,xi一定为0;当zi为其他值时,xi可取0≤xi≤ui,故定义向量。根据分支Sl中z的值,确定ubl的值,

由此,RPl可改写为如下非线性规划问题(NLPl):

因此,对NLPl进行求解,即可得到松弛问题(RPl)的最优解。Zhao等[34]给出了一种一阶算法(VAPP),可在O(1/ε)的时间复杂度下得到NLPl模型的ε近似最优解。

根据VAPP算法,首先对进行广义Lagrangian松弛,得到(ALl):

因此,对问题(NLPl)的VAPP 算法的一般流程(VAPPl)如下式所示:

式中,πk=pk+〈1n,xk〉-1,算法的原始问题式(13)为在给定广义Lagrangian乘子pk后,对ALl进行线性化规则化,求解相应问题得到原始变量更新。对偶问题为对广义Lagrangian 乘子的更新。e是规则化参数,在具体算法流程中将以回溯的方式获取。由于在式(1f)中加入了辅助变量y,故对目标函数的线性化部分∇r(xk)会与当r(x)为式(1a)～(1e)时有所不同。对应不同算法具体流程如NLPl-1和NLPl-2所示:

(1)均值方差投资组合问题与风险价值投资组合问题的NLPl求解算法。首先讨论均值方差投资组合问题和风险价值投资组合问题,即r(x)为式(1a)～(1e)时问题(NLPl)的求解方法,求解算法(NLPl-1)步骤如下:

输入对应NLPl问题的所有参数,最大迭代次数K。

输出所需NLPl问题的解。

初始化设置初始解x0==0n,p0=0,ε=10-6,η=0.9,e0=1。

步骤1设置k=0。

步骤2终止条件。如果‖xk+1-xk‖＜ε或k=K,进入步骤7,否则进入步骤4。

步骤3计算投影:πk=pk+〈1n,xk〉-1。

步骤4求解原始优化问题。计算:

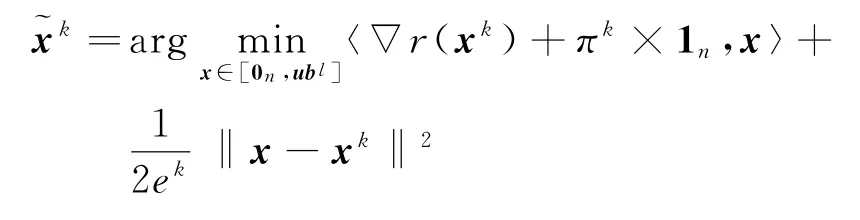
步骤5判断是否下降。如果

如果下降,则保持参数ek+1=ek,更新原始变量xk+1=,求解对偶优化问题pk+1=pk+〈1n,xk+1〉-1;如果不下降,则调整参数ek=ηek,返回步骤4,重新求解原始优化问题。

步骤6计算,k=k+1,返回步骤3,计算新迭代点的投影。

步骤7输出。

步骤4中,不同r(x)模型对应的梯度∇r(x)如表2所示。

表2 式(1a)～(1e)对应不同r(x)形式和梯度∇r(x)表

原始优化问题为

根据一阶条件,可以得到原始优化问题的最优解的闭合表达式为:

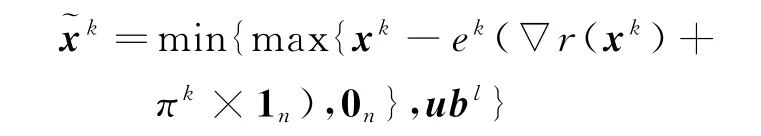
(2)损失函数投资组合问题(NPLl)的求解算法。下面讨论损失函数投资组合问题,即当r(x)为式(1f)时问题(NPLl)的求解方法阐述,求解算法(NPLl-2)步骤如下:

输入对应NPLl问题的所有参数,最大迭代次数K。

输出所需NPLl问题的解。

初始化设置初始解x0==0n,y0=0,p0=0,ε=10-6,η=0.9,e0=1。

步骤1设置k=0。

步骤2终止条件。如果‖xk+1-xk‖＜ε或k=K,则进入步骤7,否则进入步骤4。

步骤3计算投影:πk=pk+〈1n,xk〉-1。

步骤4 求解原始优化问题。计算:

步骤5判断是否下降。如果

则保持参数ek+1=ek,更新原始变量xk+1=,yk+1=,求解对偶优化问题pk+1=pk+〈1n,xk+1〉-1;否则,调整参数ek=ηek,返回步骤4,重新求解原始优化问题。

步骤6计算,k=k+1,返回步骤3,计算新迭代点的投影。

步骤7输出。

步骤4,损失函数投资组合问题中,式(1f)对应不同r(x,y)形式和梯度∇r(x,y)如表3所示。

表3 式(1f)对应不同r(x,y)形式和梯度∇yr(x,y)表

损失函数投资组合问题可分离为x和y变量两个原始问题。对于x变量的原始问题为

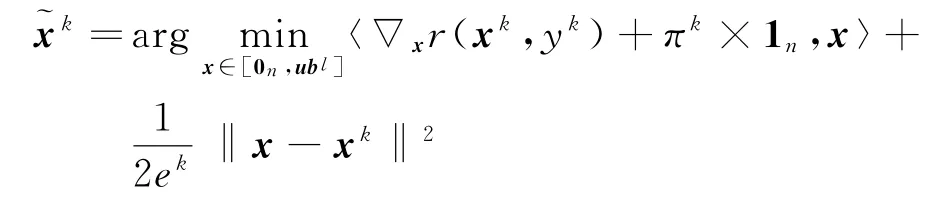
根据一阶条件,可以得到最优解的闭合表达式:

对于y变量的原始问题为

根据一阶条件,可以得到最优解的闭合表达式:

5 计算实验

本文计算实验运行环境:处理器为Intel(R)Core(TM)i5-6200U;内存为8 GB;操作系统为64位Windows 10;编程语言为matlab R2014b。选择Fama-French(FF)基准测试数据集[32]中5、10、12和17这4组产业投资组合数据作为实验基础数据。

本节进行两组实验:

实验1验证本文算法对问题(P)求解的精确程度。在实验1中选择较为简单的r(x)形式,当r(x)为式(1a)时的基数约束投资组合模型为混合整数二次规划。混合整数规划商用求解器Gurobi可对该问题进行精确求解。在实验1中将本文算法的求解精度和Gurobi的求解精度进行展示,说明本文算法可精确求解基数约束的投资组合问题。

实验2本文算法对问题(P)的其他较为复杂形式的模拟实验。选择r(x)为式(1b)～(1c)时的基数约束投资组合模型,该模型为混合整数非线性规划,目前尚无商用软件可直接进行求解,在实验2中将对本文算法的求解问题规模和计算时间之间的关系进行分析。

5.1 实验1:本文算法求解精确程度验证

考虑基数约束的均值-方差模型:当r(x)为式(1a)时,本文模型可表示为带约束的二次混合整数规划(Pa):

上述模型可用本文提出的算法和商业软件Gurobi进行求解。本节以Fama-French(FF)基准测试数据集中5、10、12和17这4组产业投资组合数据计算样本协方差矩阵Q和样本均值μ,选择γ=500,基数τ=2,分别应用本文算法和Gurobi软件求解,对比两种方法的计算时间、约束满足程度以及目标函数值。这里以‖〈1n,x〉-1‖ 测度约束式(2)的满足程度,以max{‖x‖0-τ,0}测度约束式(4)的满足程度。由表4可看出,本文算法可精确求解问题(Pa)。

表4 P1a计算结果与程序运行时间展示

5.2 实验2:混合整数非线性规划形式求解效果分析

考虑基数约束的风险价值模型:当r(x)为式(1b)～(1e)时,本文模型可表示为带约束的混合整数非线性规划(Pb-Pe):

式中,cβ可取ζβ、ηβ、等4种形式。目前尚无可直接求解这一模型的商业软件,故采用本文提出的算法求解。本节以Fama-French(FF)基准测试数据集中5、10、12和17这4组产业投资组合数据计算样本协方差矩阵Q和样本均值μ,选择r(x)为式(1b)～(1c)形式,β=0.9,0.95,0.99,则对应cβ取值如表5所示。选择基数τ=2,得到的投资组合问题计算时间与目标函数值如表6所示。

表5 参数选择

表6 计算结果与计算时间展示

由表6数值实验结果,对计算时间进行统计分析得图2、3。由图中可以看出,本文提出的方法可以在很短的时间内有效处理基数约束产业投资组合优化问题。但是,随着规模的增加,由于分支定界算法自身劣势,求解时间会快速增长。

图2 不同算例计算时间图

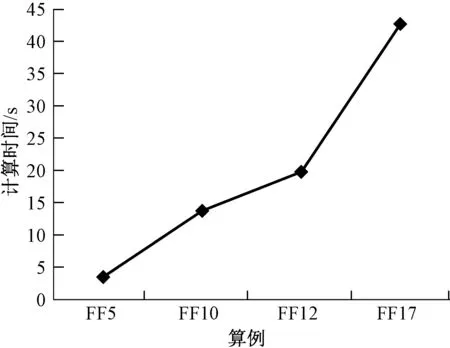
图3 不同规模算例平均计算时间图

6 结语

本文研究基数约束投资组合模型,该模型以最小化风险函数为目标,在不允许卖空前题下,考虑基数约束和预算约束。该模型应用极其广泛,包含带基数约束的均值-方差模型、VaR 和CVaR 模型等。本文将该模型用非线性混合整数规划模型来刻画,目前尚无商用软件可以求解得到这一问题的全局最优解。针对这一类问题提出一种全局最优化算法,在分支定界法框架基础上,以有效的一阶算法求解的下界松弛问题。最后,通过Fama-French(FF)5、10、12、17产业投资组合基准测试数据设计仿真实验。实验结果表明,本文提出的方法能有效处理基数约束产业投资组合优化问题,能够给出任意基数要求下的投资组合方案,能够帮助风险投资企业做出产业最优投资筛选决策。