基于田口法和MOPSO算法的PMSM转矩优化设计

曹 敏，杨国龙

(1.广东海洋大学 寸金学院，湛江 524000；2.湛江幼儿师范专科学校，湛江 524000)

0 引 言

永磁同步电动机(以下简称PMSM)具有结构简单、控制方便、功率密度较高等特点，被广泛应用于精密仪器上，包括机床、机器人、医学器材等设备[1-4]。对于PMSM来说，为了提高控制的高效性以及精度和力度，需要提高电机电磁转矩的各类参数，对电机的电磁转矩进行优化。国内外专家学者对电机电磁转矩优化提出了各类方法，包括优化定子槽型结构、优化转子磁钢结构以及优化槽极配合等。

文献[5]针对机床用直接驱动力矩电机的要求，设计一种不等定子齿顶部宽度的结构，并结合转子斜极的措施，提高了绕组利用系数，抑制了电磁转矩的波动程度。文献[6]对于电机的转矩脉动系数，采用了最小二乘法支持向量机与粒子群优化算法相结合的方式，对影响电机转矩脉动的相关系数进行了寻优分析，并利用有限元软件进行仿真验证。文献[7]采用了三维有限元仿真方法对轴向磁通永磁同步电机进行仿真分析，通过改变径向极弧系数，有效地削弱电机的齿槽转矩和电磁转矩波动。文献[8]采用解析法推导了气隙磁场与电磁转矩的计算模型，以电磁转矩参数与齿槽转矩参数作为目标，采用多目标优化方法进行优化分析，并采用有限元方法进行验证。文献[9]分析了电动汽车用集中绕组电机的力矩波动较大的原因，针对电机起动时的起动性能问题以及高速运转的转矩波动问题，对转子结构进行了设计分析和优化。

本文针对PMSM的电磁转矩进行优化，以起动转矩幅值、电磁转矩稳定值以及转矩波动系数为目标变量，以磁钢厚度、极弧系数、磁钢偏心距、定子槽口宽度为参数，以Taguchi法安排了各个参数的不同水平的合理搭配，并采用有限元软件仿真分析得到各不同搭配的电磁转矩的参数，并以此作为样本数据集合进行函数拟合，最后采用多目标粒子群优化算法(以下简称MOPSO算法)进行寻优得到最优解，并用有限元软件进行验证分析。

1 PMSM电磁转矩产生机理分析

对于PMSM来说，当定子绕组中通以对称三相电流，定子磁场与位于转子上的磁钢产生的永磁体磁场相互作用，从而产生了电磁转矩。假定当铁心处于不饱和状态且转子无阻尼绕组的影响，可以得到d,q坐标系下的PMSM的电压方程与磁链方程[10-12]：

(1)

(2)

式中：ud与uq分别为d轴与q轴电压；id与iq分别为d轴与q轴电流；ψd与ψq分别为定子直、交轴磁链；Ld与Lq分别为定子直、交轴电感；r1为定子绕组相电阻；ψf为永磁体基波磁场在定子绕组中产生的磁链。

则PMSM的电磁转矩可以表示：

Te=p[ψfiq+(Ld-Lq)idiq]

(3)

理想状况下，定子电流与反电动势都是正弦波，且气隙磁场与永磁体磁场谐波含量很少时，电磁转矩几乎为恒定值。而事实上，由于气隙磁场谐波与永磁体磁场谐波的存在，电机的电磁转矩不可避免地含有大量的谐波分量，且不同谐波分量的电动势与电流会相互作用产生纹波转矩。另外，对于永磁电机的特殊结构来说，当定转子相对运动时，磁钢两侧对应的小段气隙的区域内，磁导变化较大，引起磁场储能变化，从而产生齿槽转矩[13-14]，故其电磁转矩表达式:

Te=Tavg+Tcog+Thar

(4)

式中：Tavg为稳定平均电磁转矩；Tcog为电机齿槽转矩；Thar为纹波转矩。

对于纹波转矩，假设磁场不饱和，定子绕组Y型链接无中线且空间分布三相对称，则感应电动势中无3次谐波，以5次、7次谐波为主，并假设相电流为正弦波，则稳定平均电磁转矩和纹波转矩表达式[14]：

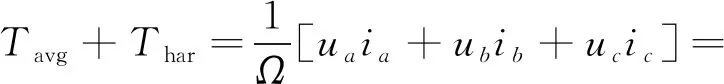
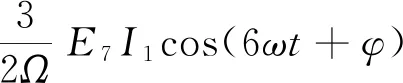
(5)

式中:E1,E5,E7分别为基波、5次、7次谐波相电压幅值；I1为基波相电流幅值；Ω为机械角速度；φ为定子相电流与相电压的相位差。

由式(5)可以看出，感应电动势的基波与相电流相互作用产生稳定平均电磁转矩Tavg，而感应电动势的谐波分量，则会与相电流产生纹波转矩Thar。

齿槽转矩表现为电枢绕组不通电时，定转子相互作用产生的电磁转矩，其表达式[2]：

(6)

式中：La为定子铁心轴向长度；R1与R2分别为定子内半径与转子外半径；n为使nz/(2p)为整数的整数。

2 Taguchi法分析与函数拟合

2.1 PMSM有限元模型建立

本文以一款36槽8极PMSM为例，进行仿真分析，其相关基本参数如表1所示。根据表1数据，利用有限元软件ANSYS Maxwell 2D建立PMSM有限元模型，如图1所示，其仿真分析得到的电磁转矩曲线如图2所示。由图2可知，起动转矩幅值Tmax为900.608 2 N·m，按照电机稳定运行时间段内计算电磁转矩稳定值Tavg以及转矩波动系数Krip，其值分别为373.606 0 N·m以及2.825%。

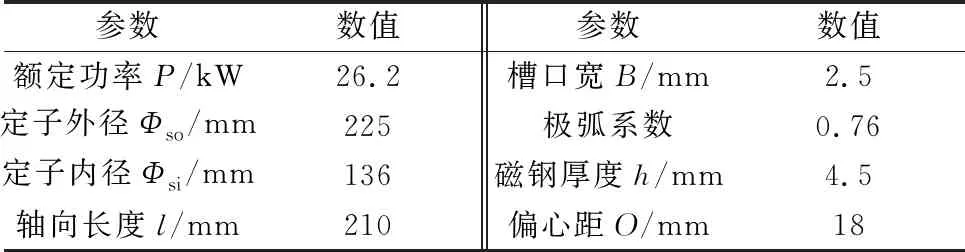
表1 PMSM初始相关参数

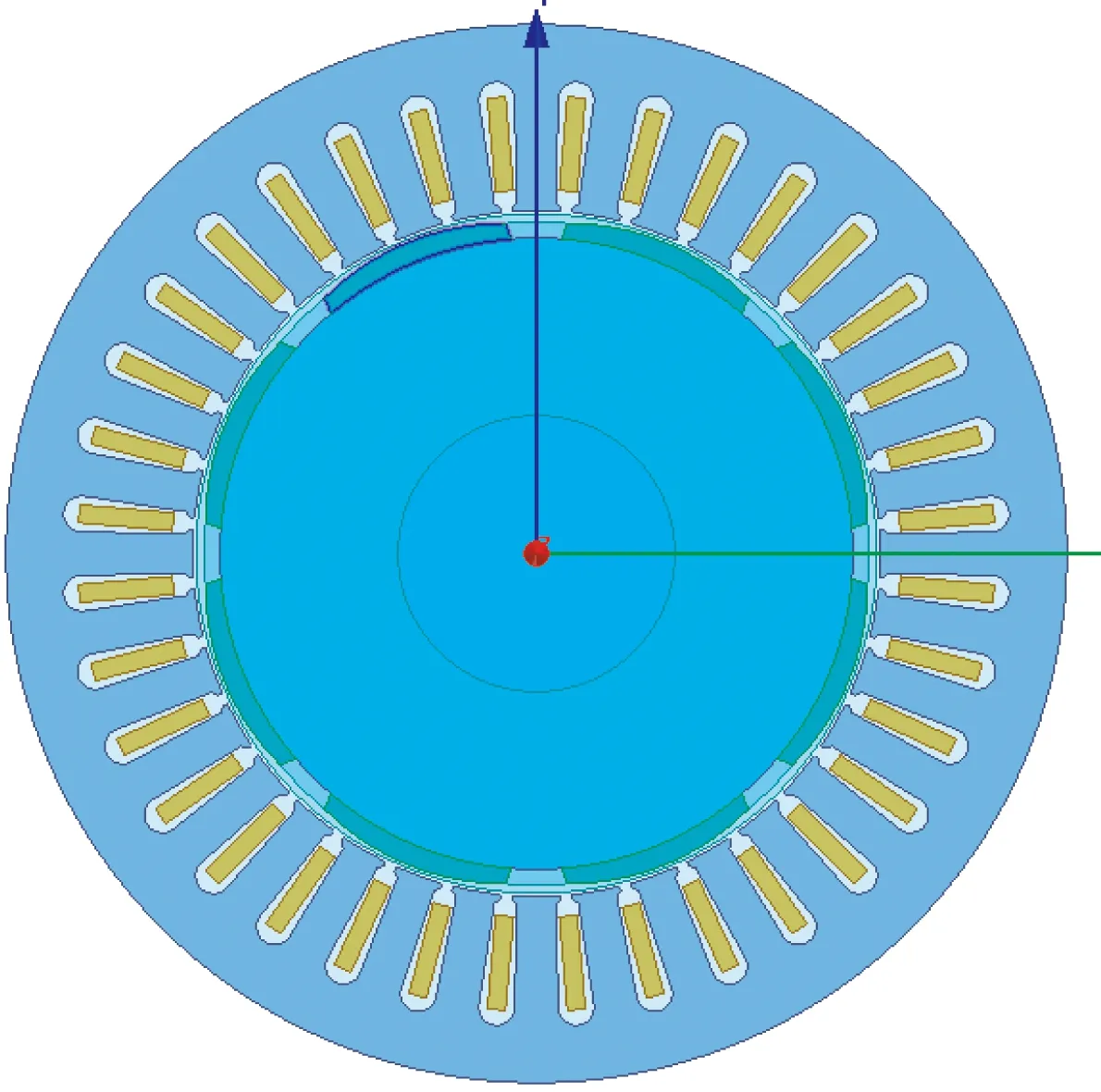
图1 PMSM初始有限元模型

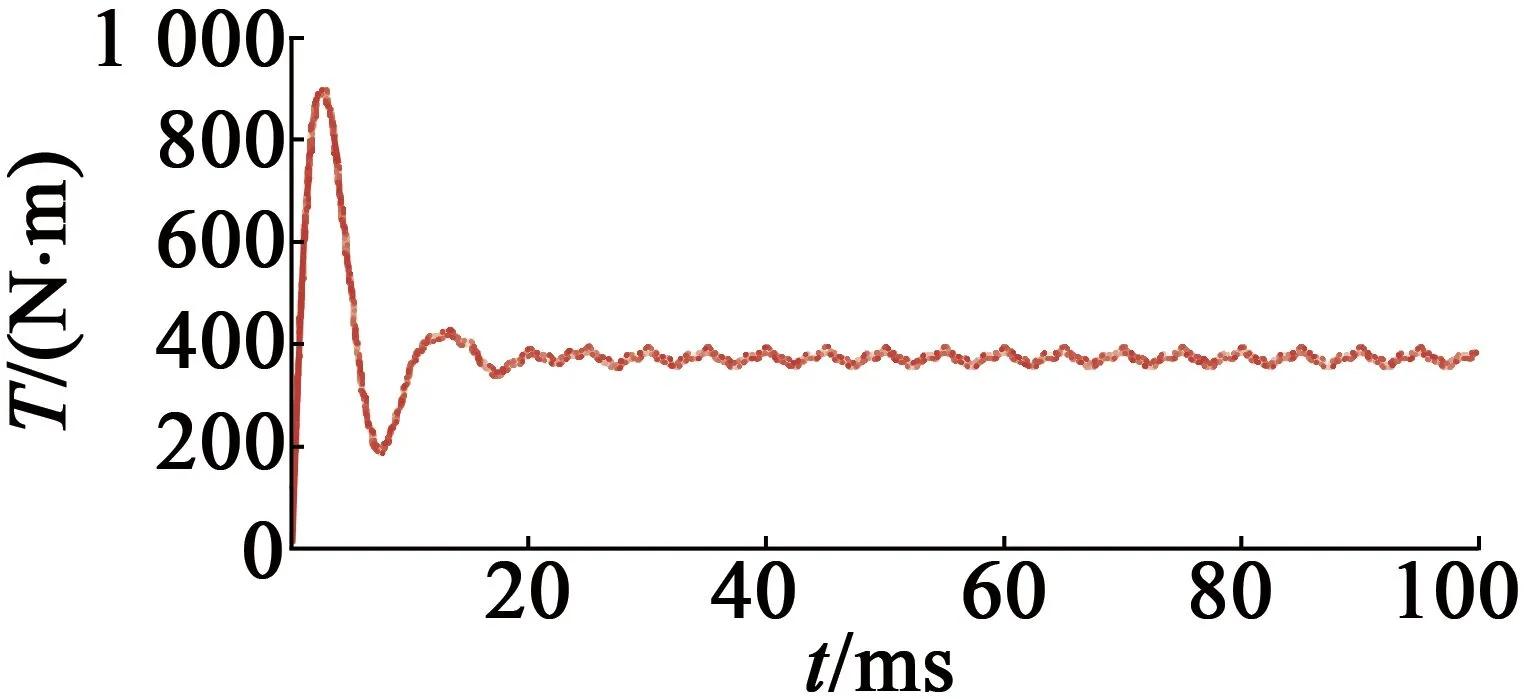
图2 PMSM电磁转矩曲线

2.2 Taguchi法实验设计与分析

本文采用磁钢厚度、极弧系数、磁钢偏心距、定子槽口宽度为参数，以起动转矩幅值、电磁转矩稳定值以及转矩波动系数为目标变量，对PMSM电磁转矩进行优化。按照电机的实际工艺情况，各尺寸参数取值范围：

(7)

式中：h,αp,O,B分别为磁钢厚度、极弧系数、磁钢偏心距、定子槽口宽度。

采用Taguchi法对各个变量正交实验，即不同因素水平进行合理的组合搭配，给出因素水平表如表2所示，可以看出,每个变量皆含有4个水平。按照正交表的要求，选定L16(45)正交表，去除第五列后采用，则可得其实验搭配及顺序如表3所示。利用有限元软件仿真分析不同参数水平搭配下的电磁转矩目标变量，即Tmax，Tavg，Krip如表3后三列所示。

表2 参数水平表

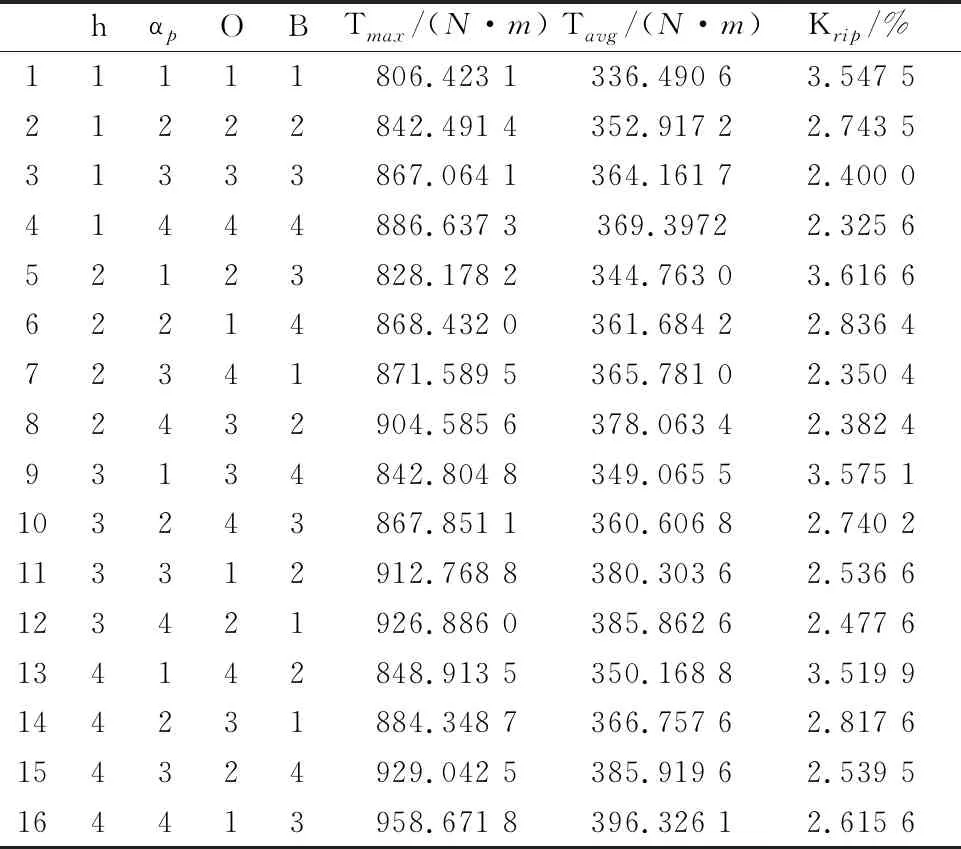
表3 正交设计表

2.3 目标函数拟合

以表3为样本数据，采用最小二乘法对Tmax,Tavg,Krip的函数进行拟合，拟合结果如下：

Tmax=-17.65+119.13h+370.74αp+

16.01O+49.32B+4.35hαp-1.91hO-

0.93hB-7.10αpO+12.10αpB-2.10OB

Tavg=-28.73+43.55h+229.33αp+11.26O+

4.72B-11.72hαp-1.44hO+8.33hB-

2.27αpO-5.46αpB-1.78OB

Krip=5.65+1.76h-1.16αp-0.17O-

2.79B+0.07hO+1.11αpB+0.19OB

其方差分析如表4～表6所示。对Tmax,Tavg,Krip拟合函数进行方差分析，其决定系数为0.996 2、0.989 9、0.856 7，大于0.85，说明参数对于目标函数的解释程度高，变量之间关系显著，且三个拟合函数的回归分析的P值皆小于等于0.1，说明模型显著性较强，拟合程度较高，统计学意义明显。

表4 Tmax函数方差分析

表5 Tavg函数方差分析

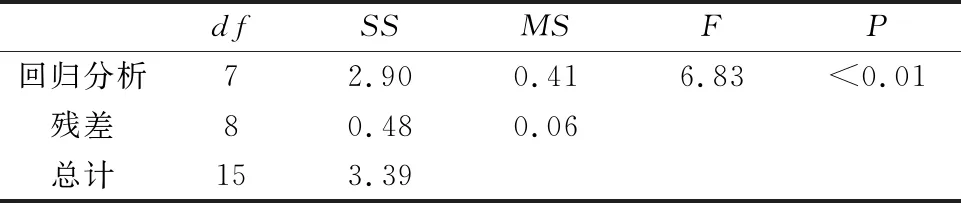
表6 Krip函数方差分析

3 MOPSO算法寻优与有限元验证

3.1 MOPSO算法寻优

粒子群优化算法是模拟大自然中鸟类觅食的行为而构建的一种人工智能算法，其根据粒子的移动位置以及移动方向、速度进行寻优。对于MOPSO算法来说，算法的运算结果及其执行效率很大程度上依赖于Pareto最优解的质量，衡量质量的方面包括解的多样性和均衡性，求解Pareto最优解的过程就是在各种指标之间平衡的过程[15-18]。MOPSO算法的步骤如下:

(1) 种群粒子初始化，包括初始化粒子速度与位置；

(2) 计算粒子适应度，按照支配关系计算非支配解集；

(3) 更新外部档案集的解，并删除部分质量差的解；

(4) 更新Pbest粒子，根据Pareto支配关系进行粒子更新；

(5) 在外部档案集中选择一部分粒子作为Gbest；

(6) 更新粒子中属性，即位置与速度；

(7) 迭代与终止。

按照MOPSO算法，设置粒子个数为30个，迭代次数为5 000次，对Tmax，Tavg，Krip的函数进行多目标寻优。寻优目标为Tmax和Tavg最大且Krip最小，参数取值范围如式(7)所示。

寻优结果如图3所示。可以看出，Tmax的解区间位于944.971 1N·m～962.073 9N·m之间，Tavg的解区间位于391.947 6N·m～398.783 4N·m之间，Krip解区间位于1.454 6%至1.682 9%之间。按照起动转矩幅值较大、电磁转矩稳定值较大以及转矩波动系数较小的原则，对Pareto解空间进行筛选，选取参数：h=4.688 8mm；αp=0.899 0；O=16.539 9mm；B=2.7830mm，则其对应的Tmax,Tavg,Krip分别为962.0739N·m，398.7834N·m，1.4546%。

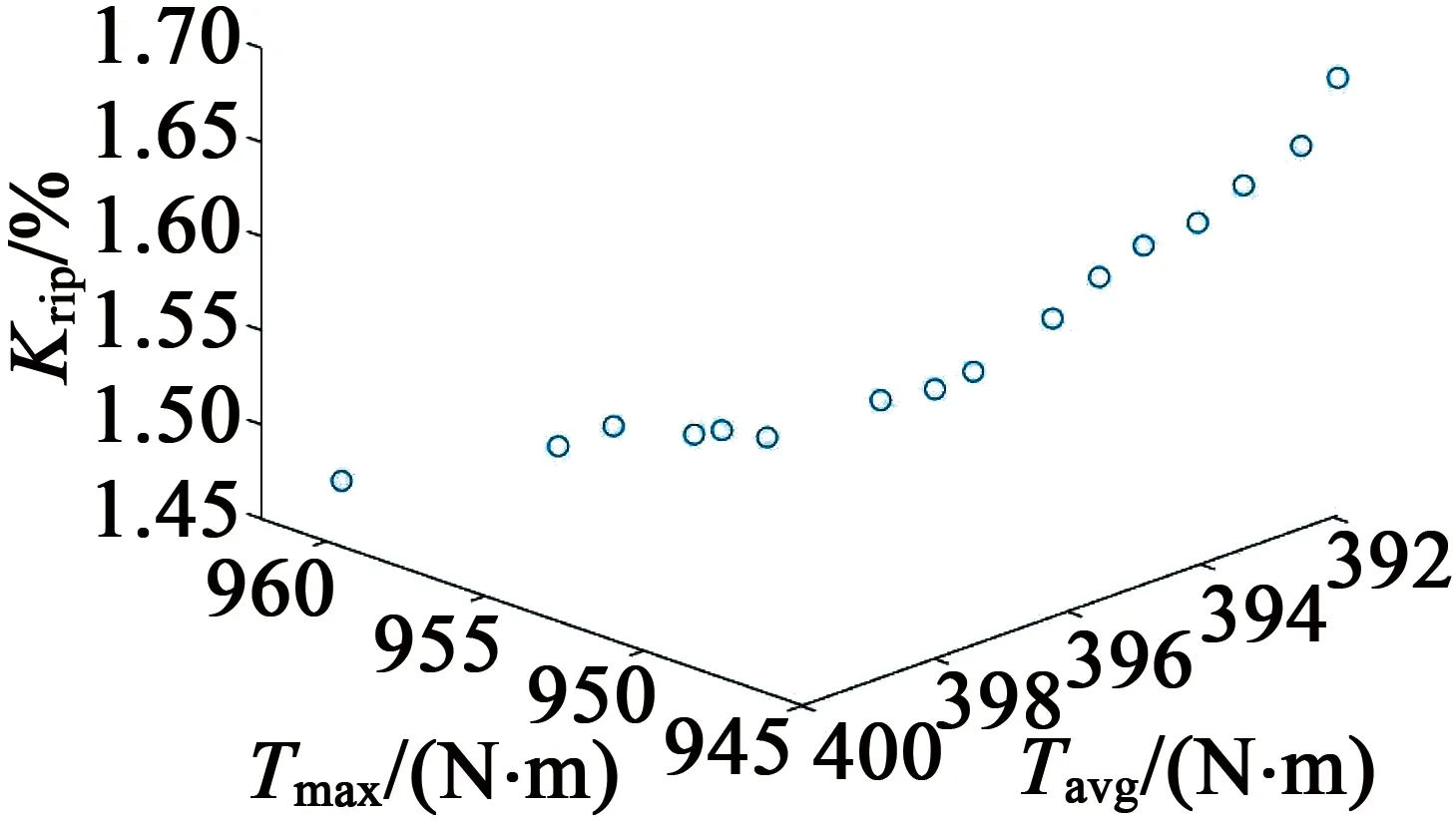
(a) 三维空间分布

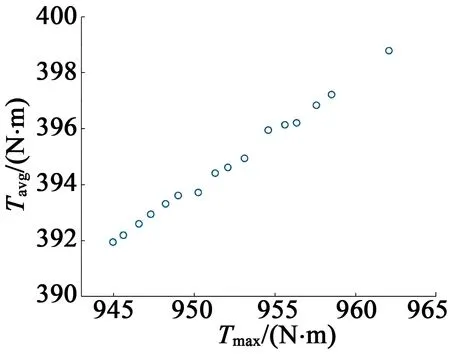
(b) Tmax与Tavg

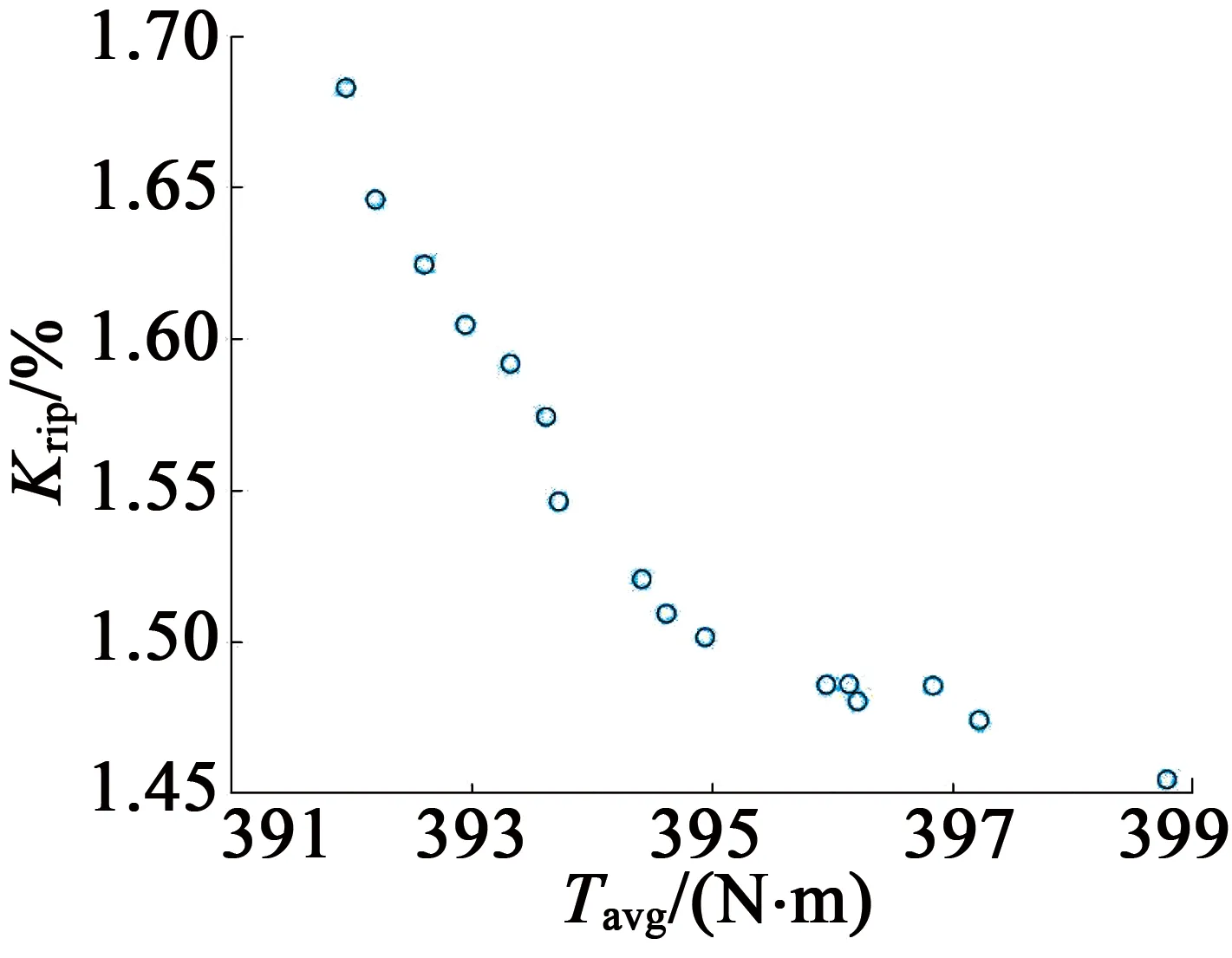
(c) Tavg与Krip

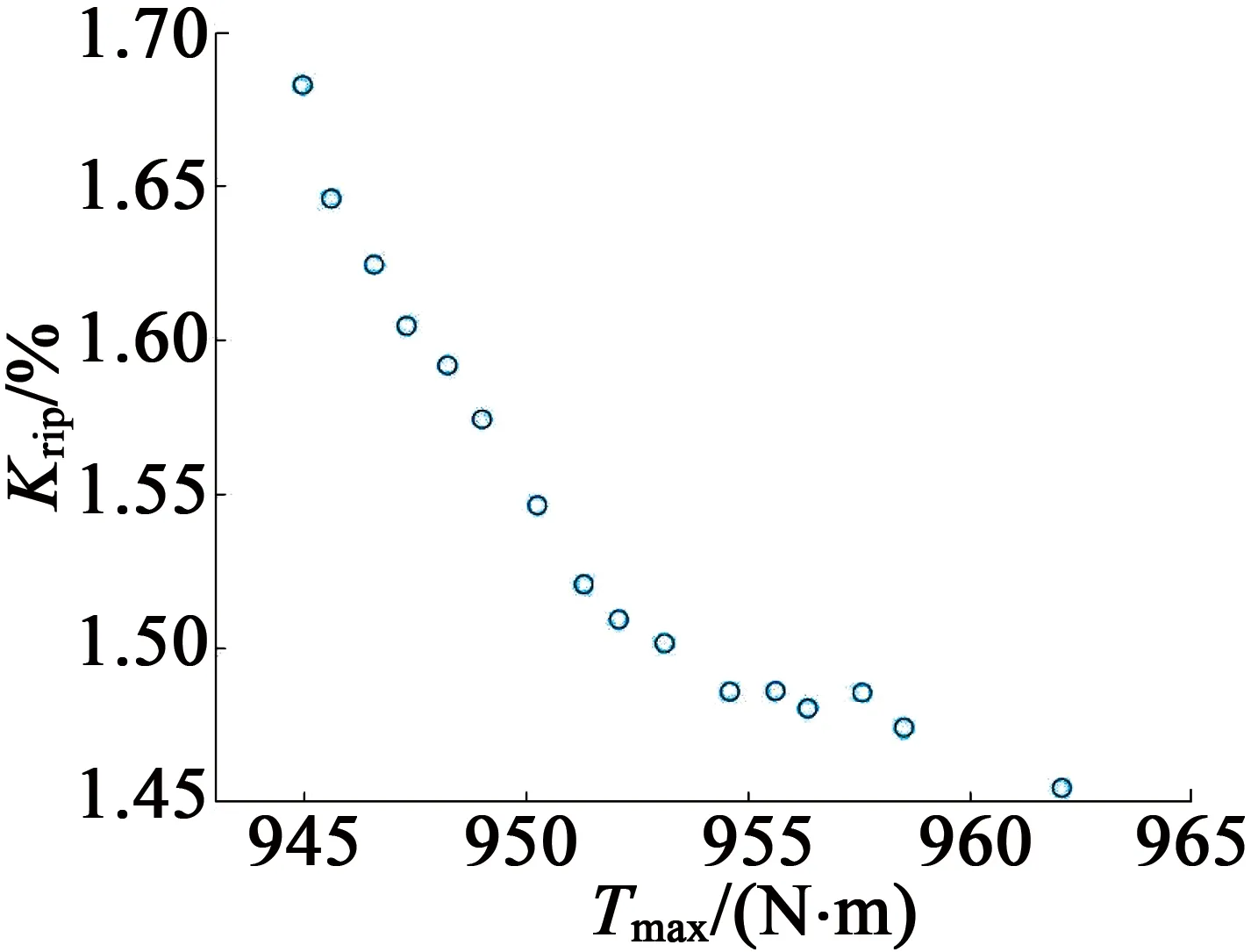
(d) Tmax与Krip

3.2 有限元验证

对MOPSO算法得出的解，通过有限元方法进行验证分析。将磁钢厚度h、极弧系数αp、磁钢偏心距O、定子槽口宽度B分别取值为4.68mm、0.89、16.53mm、2.78mm，并建立PMSM有限元模型进行仿真分析，结果如图4所示。可以看出，起动转矩幅值为962.103 9N·m，相较于优化前上升了6.83%；电磁转矩稳定值为398.938 4N·m，相较于优化前上升了6.78%；转矩波动系数为1.545 6%，相较于优化前下降了45.28%。以上分析结果与MOPSO算法得出的结果相近，验证了该算法在电机电磁转矩优化方面的有效性。

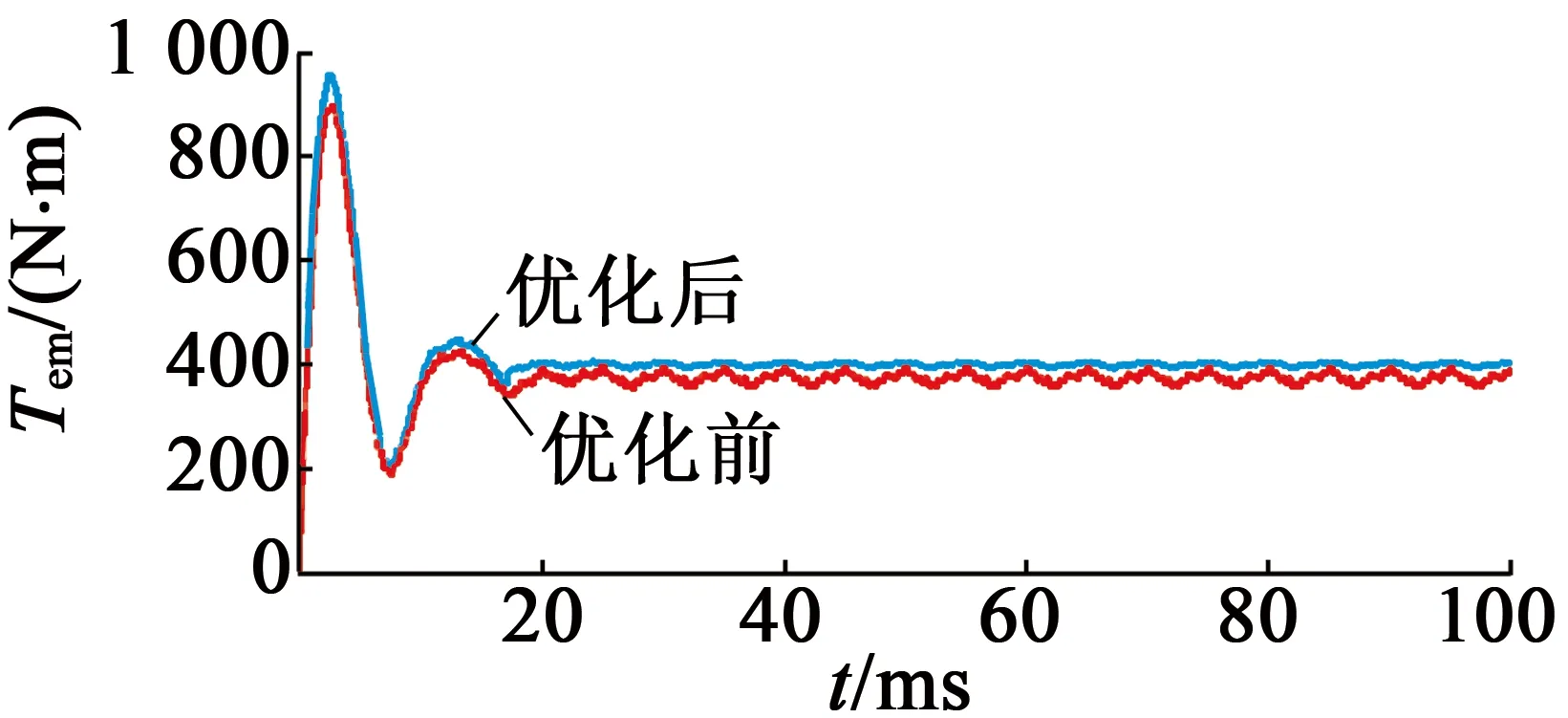
图4 优化前后PMSM电磁转矩曲线

4 结 语

本文针对于PMSM的电磁转矩要求，以一款36槽8极PMSM为例，进行优化设计，以起动转矩幅值、电磁转矩稳定值以及转矩波动系数为目标变量，以磁钢厚度h、极弧系数αp、磁钢偏心距O、定子槽口宽度B为参数，利用Taguchi法安排了正交实验进行仿真分析，并利用最小二乘法进行了拟合，对拟合函数进行了方差分析，拟合模型较优，解释程度较高。采用MOPSO模型对3个目标变量进行寻优，得到的结果利用有限元软件进行仿真验证，仿真结果验证了基于Taguchi法的MOPSO算法的有效性与准确性。