钢纤维混凝土冲击性能的有限元研究

徐佳兴，王英涛，*鲁志雄，雷元新

（佛山科学技术学院 交通与土木建筑学院，广东 佛山528000）

钢纤维混凝土凭借其良好的力学性能成为当下研究的热点课题。在静力学方面，牛龙龙［1］、陈从春［2］和FANG［3］等对多种体积参量的钢纤维混凝土进行了实验研究，结果表明钢纤维的掺入对强度均有增强作用的结论，而且能改变混凝土的失效模式。在对钢纤维混凝土冲击动力性能的研究上也有较多探索。巫绪涛等［4］利用大直径SHPB 装置对不同体积分数的钢纤维高强混凝土进行了4 种应变率下的冲击压缩实验，发现随着应变率增大，应变率效应逐渐减弱。杨惠贤等［5］对纤维总体积参量为2%的PVA/钢混合纤维水泥基复合材料进行了冲击实验，发现本构曲线的应变硬化现象随钢纤维含量增加而更加突显。焦楚杰等［6］对钢纤维混凝土进行了冲击劈裂实验，发现钢纤维混凝土韧性和耗能能力随钢纤维含量的提高而增强。实验研究虽然能得出确信的实验数据，但需耗费大量资源且无法穷尽各种可能。有限元模拟是一种有效的代替方案，但在利用ANSYS/LS-DYNA 有限元软件对SHPB 实验进行数值模拟研究方面成果较少。焦楚杰等［7］利用LS-DYNA 有限元软件对钢纤维高强混凝土的冲击性能进行数值模拟，采用弹塑性流体动力本构模拟钢纤维高强混凝土，通过控制强度和失效应变两个参数来表现钢纤维对材料的增强效果，结果表明应力峰值和试件的破坏不是同时发生的，且破坏滞后发生。刘永胜等［8］根据SHPB 实验提出了一种简化的包含纤维增强因子、应变率增强因子和损伤量D 的钢纤维混凝土本构，通过该本构拟合出的本构曲线能反应钢纤维混凝土冲击过程中的应力行为特征。曹吉星［9］提出利用BP 神经网络遗传算法对SHPB 实验数据进行学习和训练，得出钢纤维混凝土的神经网络本构，但这需要以大量实验数据为基础。杨惠贤［10］同样在HJC 本构基础上改进现有本构，先进之处在于得出各因子与纤维特征参数的关系式，充分考虑了纤维特征的影响，数值模拟结果显示相对误差为4%。陈猛等［11］等对钢/聚丙烯混杂纤维混凝土和钢纤维混凝土进行了SHPB 冲击实验，同时还利用HJC 本构进行了模拟，结果表明重构的应力-应变曲线与实验曲线吻合较好，峰值应力最大误差为3.84%。

本文以文献［11］中的实验为基础，利用ANSYS/LS-DYNA 有限元软件，采用HJC 本构钢纤维混凝土SHPB 实验进行数值模拟研究。

1 模拟对象

文献［11］采用图1 所示直径74 mm 直锥变截面分离式SHPB 装置进行钢纤维混凝土抗冲击性能实验。试件采用的胶凝材料为P.O42.4 级水泥，钢纤维选用端勾型钢纤维，纤维掺入量为50 kg/m3，设计强度为CF50。试件为直径70 mm，厚度35 mm 的圆柱体，共进行了21 s-1、46 s-1、66 s-1和117 s-14 种应变率下的冲击压缩实验。

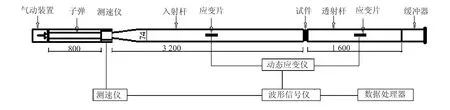
图1 SHPB 装置简图

根据一维弹性波理论和均匀性假定，可由二波法［12］计算得到试件的应变率ε˙（t）、应变ε（t）和应力σ（t），公式如下

2 钢纤维混凝土动态本构HJC 模型

Holmquist-Johnson-Cook（HJC）［13］模型是一种常见的率相关损伤型本构模型，广泛用于混凝土材料的高应变率冲击实验的数值模拟。HJC 模型的方程表达式为

式中σ*、P*分别为标准化的等效应力和静水压力，ε*为实际应变率与参考应变率的比值；A 为内聚力强度，D 为损伤度，B 为压力硬化系数，N 为压力硬化指数，C 为应变率系数。HJC 模型的主要参数见表1。由于部分实验数据不完整，本文中采用的本构参数结合文献［10］，对表观密度、剪切模量和A 值进行了调整。

表1 HJC 本构模型材料参数

HJC 模型的状态方程描述的是静水压力和体积应变的函数关系，具体表现为一个3 段式的方程［14］，见图2。该方程共分为3 个阶段：线弹性阶段（OA 段）、塑性变形阶段（AB 段）和完全密实阶段。

HJC 模型是以材料的等效塑性应变和塑性体积应变的累加来定义材料的损伤，损伤演变方程为

其中D 定义为材料的损伤度，Δερ和Δμρ分别为等效塑性应变增量和塑性体积应变增量，εfρ和μfρ分别为常压下混凝土破碎的等效塑性应变和塑性体积应变。

图2 HJC 状态方程曲线

3 有限元模型

模型中的子弹、入射杆和透射杆为钢制材料，在模拟中采用线弹性材料模型，材料参数为：ρ=7 680 kg/m3，E=210 GPa，v=0.29。实验装置和混凝土试件均采用Solid164 实体单元。子弹、入射杆和透射杆单元网格尺寸设置为0.008 m，试件的单元网格尺寸设置为0.002 m，鉴于模型计算量适中，且为了保证模拟的准确度，本模拟建立全模型图。网格划分如图3～5 所示。模型中子弹和入射杆接触面采用普通的自动面面接触（ASTS），入射杆和透射杆与试件的接触面均采用侵蚀面面接触（ESTS）。侵蚀接触的特点在于当试件表面单元被侵蚀破坏后由余下的单元继续形成接触关系，能真实反应冲击破坏情况。

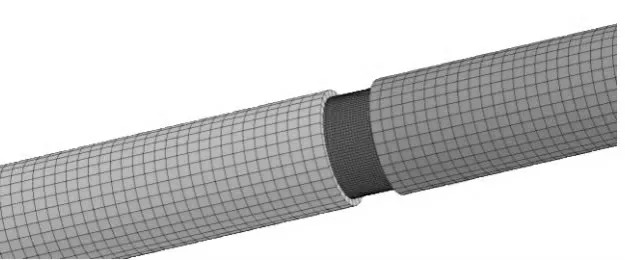
图3 模型网格划分图

图4 试件网格划分

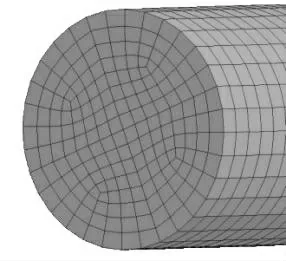
图5 压杆网格划分

4 数值模拟结果与分析

4.1 应力波图及本构曲线分析

基于上述有限元模型，对文献［11］中的实验结果进行数值模拟分析，经数据处理得到平均应变率为64 s-1下的应力波图，见图6，通过对比数值模拟和实验结果可知，应力波图基本吻合。为进一步验证模型的准确性，利用数值模拟提取的应力波，根据二波法重构钢纤维混凝土的应力—应变曲线图，如图7。实验得出的4 种应变率下的应力—应变曲线图如图8。

数值模拟结果与实验实测结果对比可见，在线弹性上升段、初步损伤段和损伤剧烈演化段两者曲线走势接近，在结构破坏段则有一定差距，这是因为在后两个阶段试件发生大变形破坏，此时试件已不满足应力均匀性假定，实验和数值模拟都难以准确得出其力学行为［15］。应变率由21 s-1增加到64 s-1时，试件表现出明显的应变率效应，当应变率达到114 s-1时，峰值应力与64 s-1时的结果基本持平，应变率效应不再突出，这也符合“临界应变率”［16］的概念。

将4 组应变率下的数值模拟和实验结果曲线分别作对比分析，见图9，数据对比结果见表2。由表2可知，各组应变率下数值模拟的峰值应力均高于实验结果，且与实验测得结果的最大误差为3.68%，贴合度较好；峰值应变方面，在数值模拟应变率为21 s-1和45 s-1时，数值模拟的峰值应变高于实验测得结果，最大误差为22%，在应变率为64 s-1和114 s-1时，数值模拟结果低于实验结果，最大误差为21%。通过以上应力波图和本构曲线对比分析可知，该数值模拟分析是可靠的。

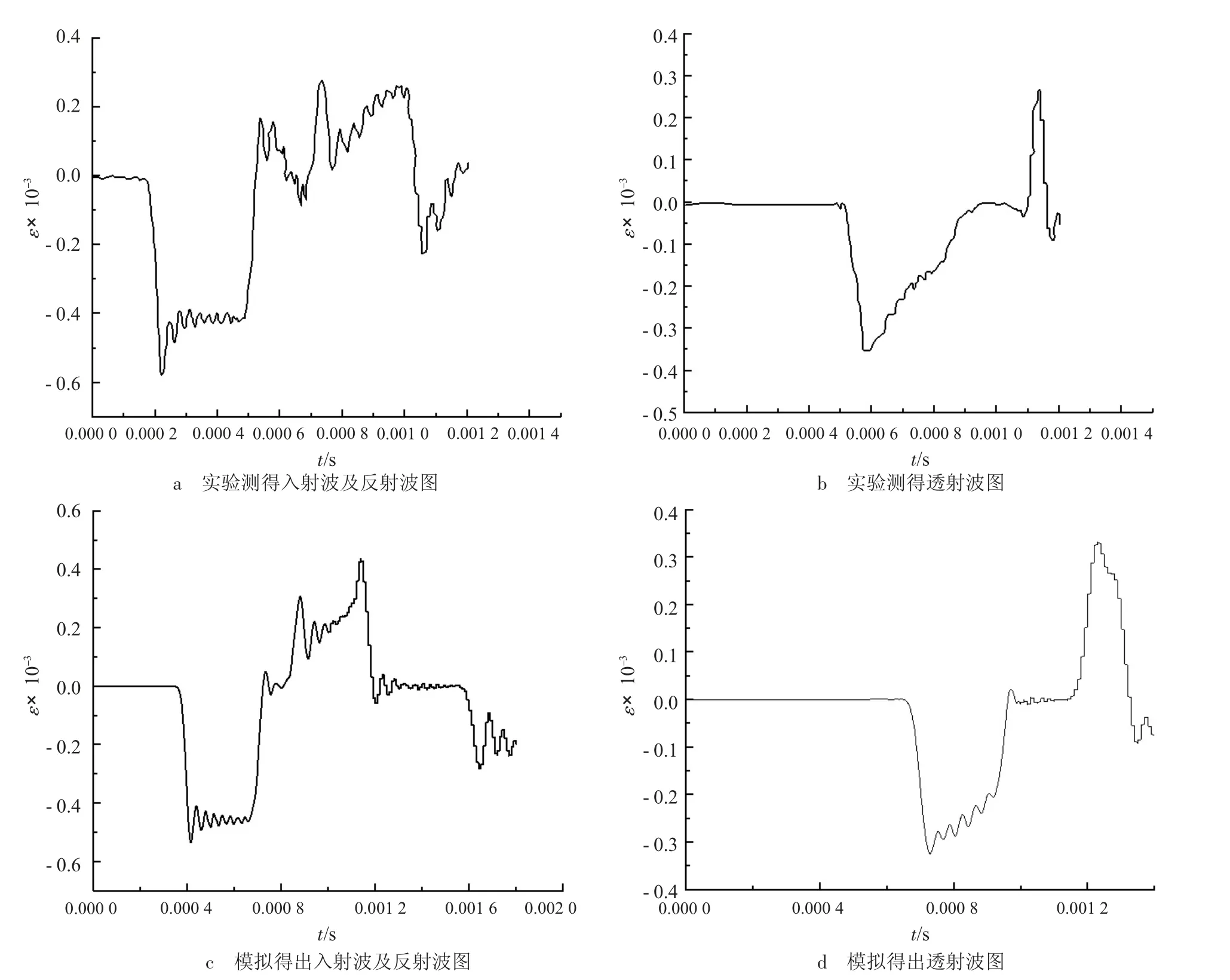
图6 应变率为64 s-1 时实验和数值模拟的三波图

图7 数值模拟得出的应力—应变曲线图

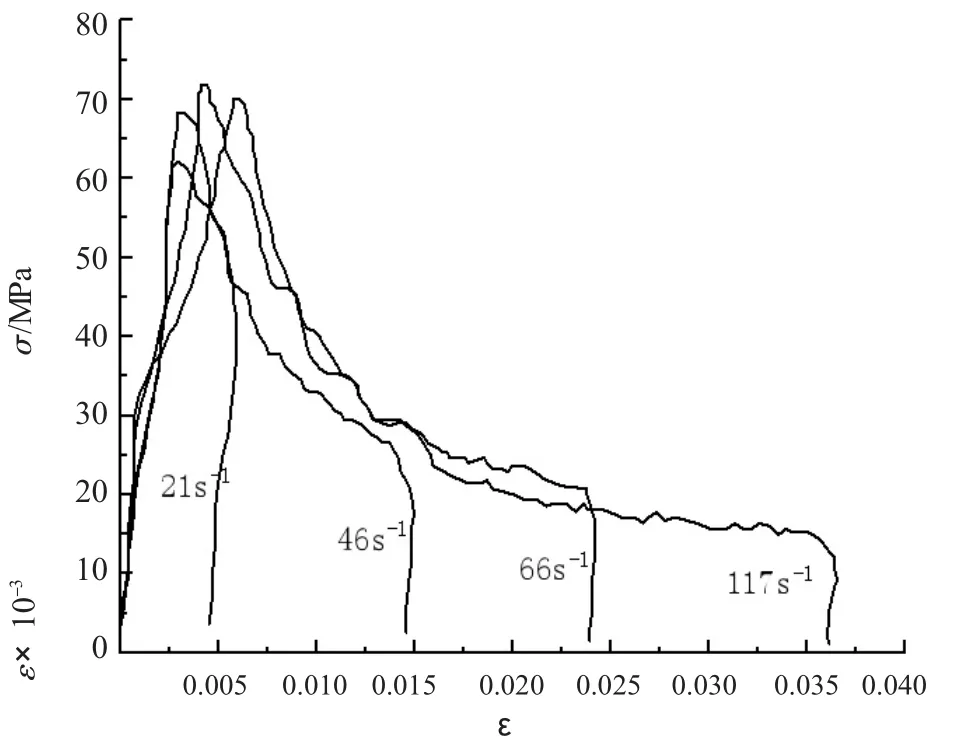
图8 实验得出的应力—应变曲线图

表2 各应变率下峰值应力和应变对比表

图9 四组应变率下应力—应变曲线对比图

4.2 试件破坏过程分析

鉴于应变率为21 s-1和45 s-1时试件未见明显破坏，故对应变率为64 s-1和114 s-1情况下的试件破坏过程进行分析，破坏过程如图10～11。

通过两种应变率下的破坏对比图可见，试件的破坏过程大致相似，其中应变率为114 s-1时各损伤阶段比64 s-1应变率下快0.1 ms 左右。以应变率为114 s-1时损伤过程为例，从图11 可观察到：在破坏初期，单元的剥离发生在试件外围边缘，随着损伤的加剧，在0.793 ms 时，试件形成外围破环圈，芯部可继续承受冲击应力波，这是由于高速冲击下试件的侧限效应导致非一维应力状态，试件芯部受到外围单元的保护作用；对比两种应变率下各时刻芯部的规则程度发现，高应变率时芯部形状越接近于圆形，而低应变率时，芯部呈现出分散破碎状，如图11c；随着试件继续承载，在0.795 ms 后试件芯部单元逐渐被完全剥离、破环。

图10 应变率为64 s-1 时试件破坏过程

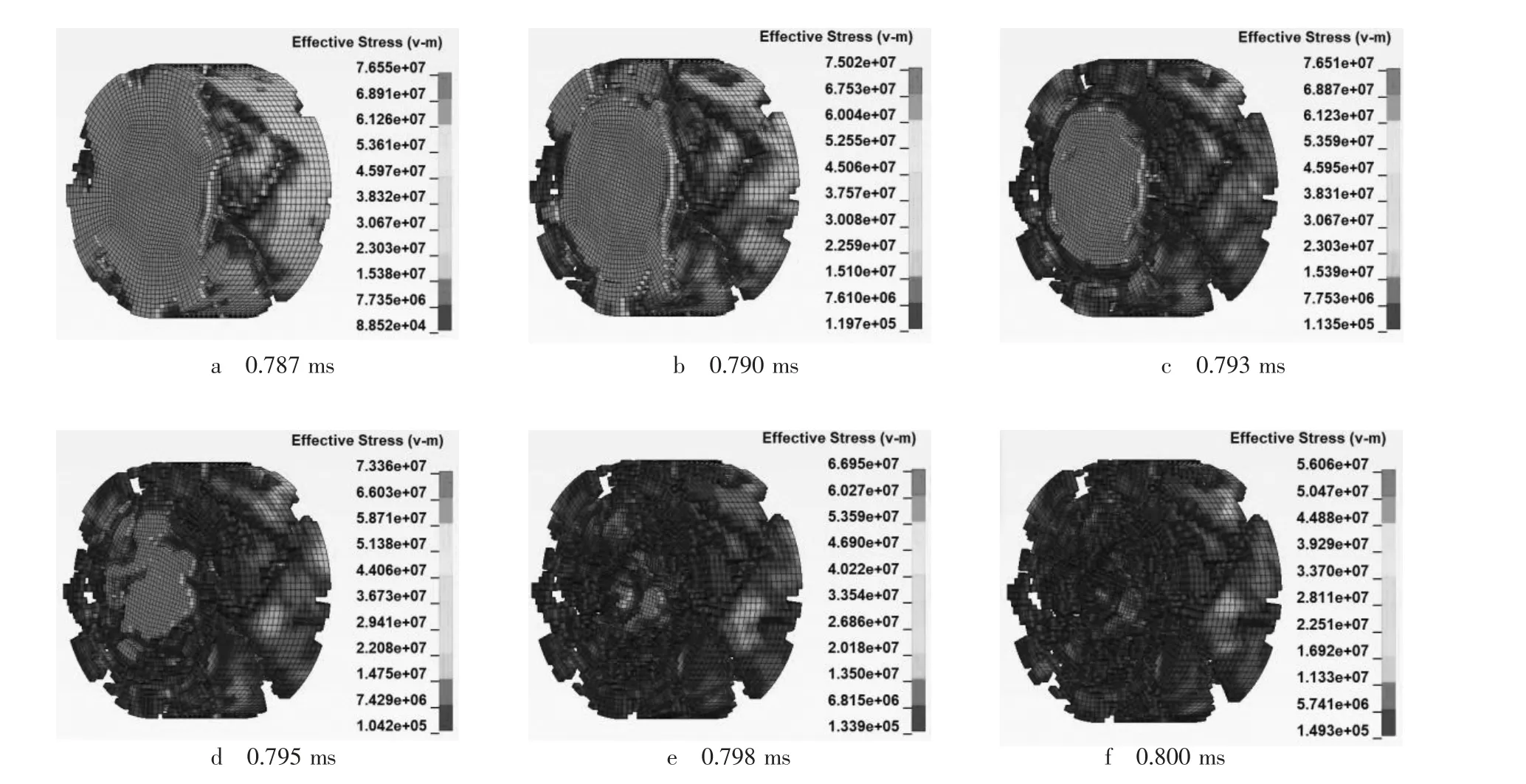
图11 应变率为114 s-1 时试件破坏过程

5 结论

（1）利用ANSYS/LS-DYNA 有限元软件建立了SHPB 实验模型，并采用修正过的HJC 本构对钢纤维混凝土进行4 种应变率下的冲击实验进行有限元模拟，得出了不同应变率下的应力-应变曲线图和试件破坏过程图。

（2）通过对比分析64 s-1应变率下的应力波图和各应变率下的应力-应变曲线图可知，模拟与实验测得结果吻合度较好，峰值应力误差不超过3.68%。同时也说明修正过的HJC 本构能较好模拟出钢纤维混凝土在各应变率冲击作用下试件的力学行为。

（3）通过对64 s-1和114 s-1应变率下试件破坏过程分析可知，114 s-1时试件损伤要比前者快0.1 ms 左右，且应变率越高时芯部形状越接近于圆形。同时，两种情况下试件的破坏都是从边缘逐渐向芯部发展，然后芯部继续承载，直至完全破。这种从外到内的破坏过程反映出高应变率破坏时的横向侧限效应。