空间连杆引纬机构柔性铰间隙动态特性研究

李 博， 胡 凯， 金国光， 魏 展， 畅博彦

(1. 天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387； 2. 天津工业大学 机械工程学院， 天津 300387)

随着纺织机械行业的迅速发展，无梭织机以其体积小、能耗低、速度快成为目前纺织机械领域的主流产品[1]。剑杆织机作为无梭织机中的典型代表，因纱线适配类型丰富、产品后期可拓展性强等特点，应用越来越广泛[2]。常见的剑杆织机引纬机构包括共轭凸轮、差动轮系、变导程螺旋、空间连杆、电子引纬等。其中，空间连杆引纬机构因运动规律易控制、传动效率高等特点，被诸如比利时PICANOL等剑杆织机生产厂商广泛应用[3]。

在空间连杆引纬机构高速运转过程中，因制造、装配、磨损等原因形成的运动副间隙必然会给系统的运行带来多种影响[4-6]。如：使系统呈现非线性特征，降低机构的运动精度，引起冲击动载荷造成运动副破坏和磨损等。

针对机构间隙的研究，始于20世纪70年代，Earles等学者提出了含间隙机构的连续接触模型，该模型将间隙等效为长度固定且无质量的间隙杆，通过间隙杆的速度突变，来判断是否发生碰撞[7]。在此基础之上，研究人员将间隙碰撞过程描述为“接触—碰撞—分离”的3种状态转化，建立了间隙运动副经典碰撞模型[8]。然而，以上模型均无法准确求解间隙碰撞力、间隙偏心距轨迹等动态特性。

要研究含间隙系统的完整动态性能，就必须考虑柔性铰间隙作用机制，建立包含弹簧力和阻尼力的非线性接触碰撞力模型[9]。早期的线性简化模型在其描述碰撞过程中没有体现柔性铰压缩和恢复过程中的能量耗散[10]。随后出现的Kelvin-Voigt线性弹性模型包含了接触刚度和阻尼，但是没有表征恢复系数和初始碰撞速度[11]。Hunt等人在Kelvin-Voigt模型的基础之上提出了Hunt-Crossley模型，奠定了现代非线性接触碰撞力模型的基本框架[12]。近年来，Lankarani、Flores、Bai等在Hunt-Crossley模型的基础上，提出了多种考虑能量耗散因素的非线性间隙碰撞力模型[13-15]。目前，国内将柔性铰间隙碰撞模型应用到空间连杆引纬机构运动学与动力学分析中的研究相对较少，相关工作的开展尤为迫切。

本文针对空间连杆引纬机构进行运动学分析，将柔性铰间隙作用机制引入到系统的动态求解中，结合Lankarani-Nikravesh模型和Newton-Euler方法建立动力学模型，研究间隙对引纬过程的直接影响，为今后剑杆织机的稳定性研究、性能优化和磨损评估等工作奠定了理论基础。

1 空间连杆引纬机构简介

剑杆织机因其换色便捷，适宜多色纬织物，而被广泛应用于色织布、双层绒类织物、毛圈织物和装饰织物的生产[16]，其引纬机构结构示意图如图1所示。

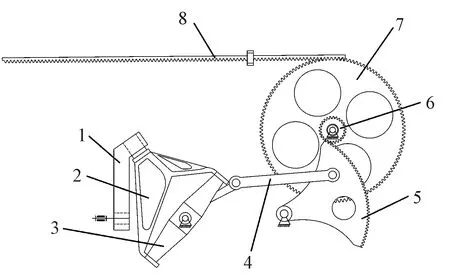
1—传动曲柄；2—空间连杆；3—十字摇轴；4—连杆；5—扇形齿轮；6—传动小齿轮；7—剑带轮；8—剑带。

剑杆织机的空间连杆引纬机构由3个部分组成，分别是空间连杆组成的运动输入部分(图1中的1、2、3)、平面连杆组成的运动传递部分(图1中的4)和由齿轮轮系、剑带、剑头组成的动程放大部分(图1中的5、6、7、8)。通过动程放大部分，可将空间连杆的运动规律放大输出到剑带和剑头处。

整个机构的构件通过大量铰接副连接，具有良好的紧凑性和运动稳定性，同时具有主轴转速高、传动路线短等优点，但该机构在运动规律设计方面较为复杂，装配精度要求较高，长时间运行，容易产生相对较大的运动副间隙;因此，有必要深入研究间隙对空间连杆引纬机构的动态性能影响。

2 柔性铰间隙接触碰撞力模型选择

本文采用柔性铰间隙模型描述机构铰间间隙碰撞(见图2)。考虑到间隙碰撞过程中运动副中心的碰撞变形，将整个碰撞运动过程描述为分离、碰撞、接触、压缩(恢复)等几种状态，通过间隙偏心距与间隙值的差值，判断碰撞是否发生。其中：RJ为轴销半径,mm;RB为轴套内径的半径,mm;c为间隙尺寸,mm。

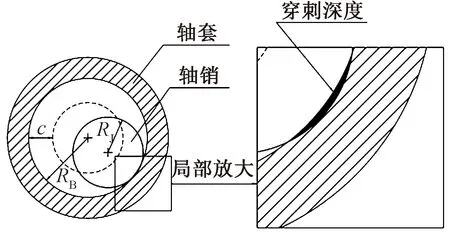
图2 含间隙转动铰模型(柔性铰)

间隙碰撞同时存在法向碰撞力和切向碰撞力，而高速剑杆织机的空间连杆引纬机构通常具有良好润滑的工况条件;因此，暂不考虑含间隙运动副中切向碰撞力即摩擦力对机构运动带来的影响。在碰撞力模型的选取中，常用的模型包括简易接触碰撞力模型、Lankarani-Nikravesh模型、Flores模型、Hunt-Crossley模型等。通过文献[18]可知：简易模型不考虑能量耗散，不能表征间隙碰撞过程中的阻尼力；Hunt-Crossley模型适用于高恢复系数的正碰撞；Flores模型适用于完全弹性或者完全塑性的碰撞环境；Lankarani-Nikravesh模型能够反映碰撞体的材料性质、几何特征及运动状态对碰撞过程的影响，其碰撞压缩与恢复阶段的能量耗散基本上相当。综上，本文选用Lankarani-Nikravesh模型描述工况下空间连杆引纬机构的间隙碰撞。

3 空间连杆引纬机构的动态建模

3.1 无间隙状态下机构的运动学分析

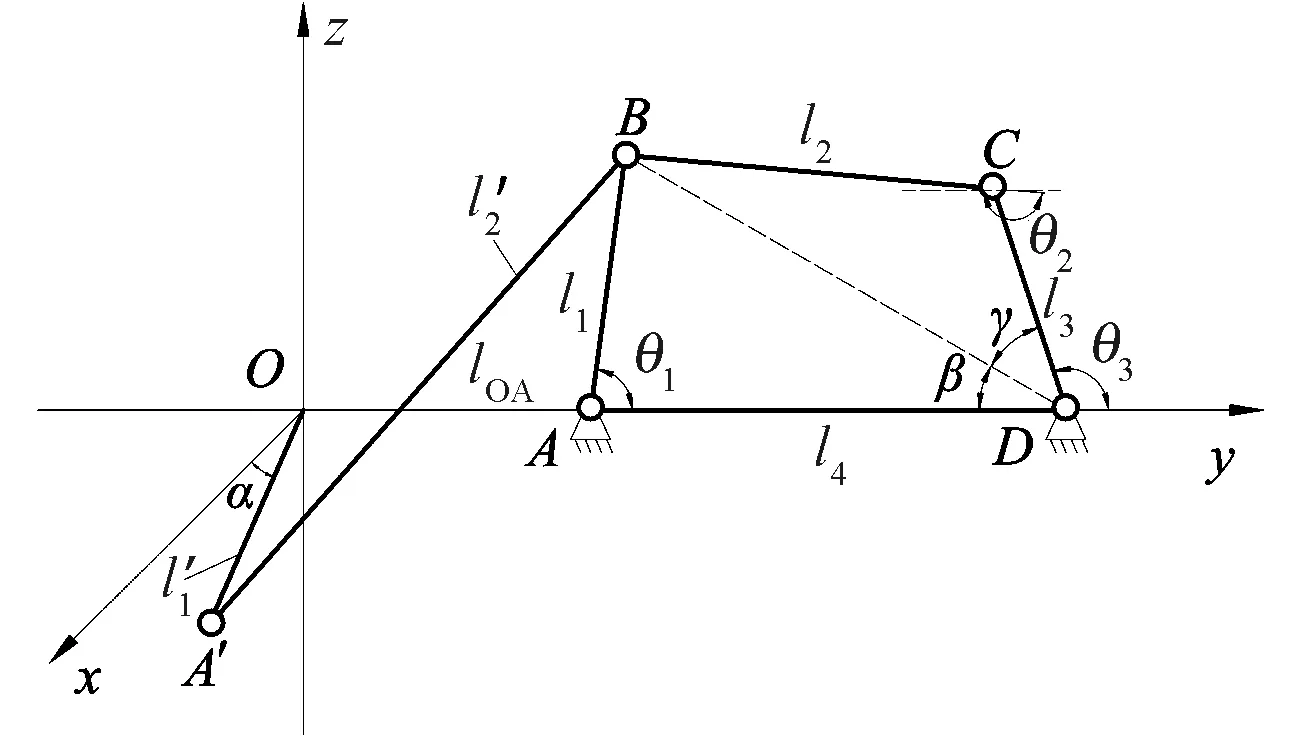
图3 空间连杆机构简化模型

首先对空间连杆部分应用矢量法建立运动学模型

(1)

将上述向量分别向x，y，z轴投影，可得到

(2)

求解可得杆BC的运动规律

(3)

通过矢量法对杆AD的运动规律求解得

(4)

(5)

由式(4)、(5)可求得θ3如下式

θ3=π-β-λ

(6)

杆CD是由扇形齿轮简化而得到的，扇形齿轮通过与小齿轮的啮合，带动剑带轮和剑带的往复运动，进而完成引纬动作,因此，剑头的运动规律可通过以下表达式求解：

(7)

式中：d1、d2、d3分别为扇形齿轮、小齿轮和剑带轮的分度圆直径，mm。

将式(7)对时间t求导，即可得到理想无间隙状态下剑头速度和剑头加速度的表达式。

本文研究对象为应用于JWG1732型高速剑杆织机中的空间连杆引纬机构，下文动力学分析和工程实例均以此机构为研究对象，不再重述。参与计算的主轴转速选择500 r/min，经过测量，d1、d2、d3分别为：250、65和369 mm，其余各构件长度见表1。

表1 各构件长度

将各参数代入式(7)并通过编程仿真，即可求解理想无间隙状态下剑头的运动学规律。运动规律如图4所示。

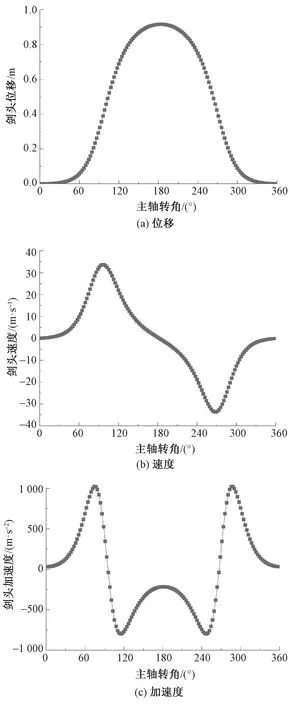
图4 理想无间隙状态下剑头运动规律

由图4可知：当主轴转角为60°～105°时，剑带带动剑头进行送纱运动，此时为了增加工作效率，需要剑头速度迅速增加；当主轴转角为105°～255°时，引纬剑头和接纬剑头进行纬纱交接，剑头加速度变化较为平缓；当主轴转角为255°～300°时，剑头回程，剑头速度呈现快速退回的运动特性;当主轴转角为300°～360°与0°～60°时，纱线准备再次进入梭口，此时剑头速度和加速度曲线相对平稳，以确保剑头准确夹持纬纱。

3.2 用于柔性铰间隙作用的动力学建模

在多体系统动力学的建模方法中，常用的方法分别是Newton-Euler方法、Lagrange方法和Kane方法。Newton-Euler方法可应用在系统构件数量有限，结构不复杂的机构中，其特点是表达式物理意义明确，拓展性强；Lagrange方法通过对系统整体动能、势能的求解，在系统构件相对较多的时候比Newton-Euler方法具有更少的方程求解量；Kane方法兼具矢量法和分析法的特点，但其求解偏速度、偏角速度等表达式物理意义不明晰，且广义速率的选取较难。综上，本文采用Newton-Euler方法对含间隙系统建立动力学模型。

图5示出含间隙连杆部分。B为含间隙运动副，s1、s2和s3分别为连杆AB、BC和CD的质心；e为间隙运动副B处的偏心距矢量；φ为偏心距矢量与y轴的夹角；F1y、F1z分别为接触碰撞力FN在y轴和z轴方向的分量。

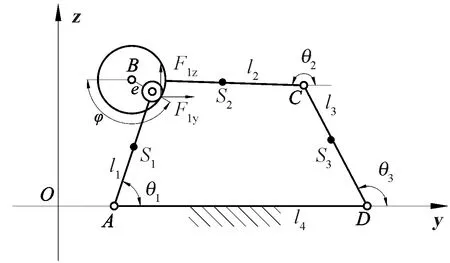
图5 含间隙连杆部分

通过前文的对比分析，接触碰撞力模型选取Lankarani-Nikravesh模型，即

(8)

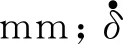
δ=e-r

(9)

式中，r为运动副间隙，mm。

间隙偏心距e与y轴的夹角为φ可表示为

(10)

通过Newton-Euler方法对系统建立动力学模型，拆分杆BC并受力分析可得

(11)

式中：R1为B运动副处的轴销半径,mm；J2为杆BC的转动惯量,kg·m2；m2为杆BC的质量,kg；F2y和F2z为C副处的约束反力在y轴方向和z轴方向的分量。杆AB和杆CD也需要通过同样的方法进行分析。

通过矢量法对B、C、D副进行描述，并整理上式可得到如下动力学方程：

(12)

(13)

式中：J3为杆CD的转动惯量，kg·m2；m3为杆CD的质量，kg。

4 工程实例分析

4.1 具体工程实例分析

在实际工业生产中，通常情况下引纬机构运动副的静态间隙为0.05 mm左右，而在高速运转过程中，运动副间隙可达到0.20 mm及以上。考虑到系统运行过程中的冲击动载荷变化及长时间运行产生磨损，以下分析的间隙取值分别为0.05、0.2和0.5 mm。另，除表1涉及的构件长度参数外，其他相关参数取值见表2所示。

表2 相关参数取值

通过模型计算可得到以下动态特性曲线，见图6所示。

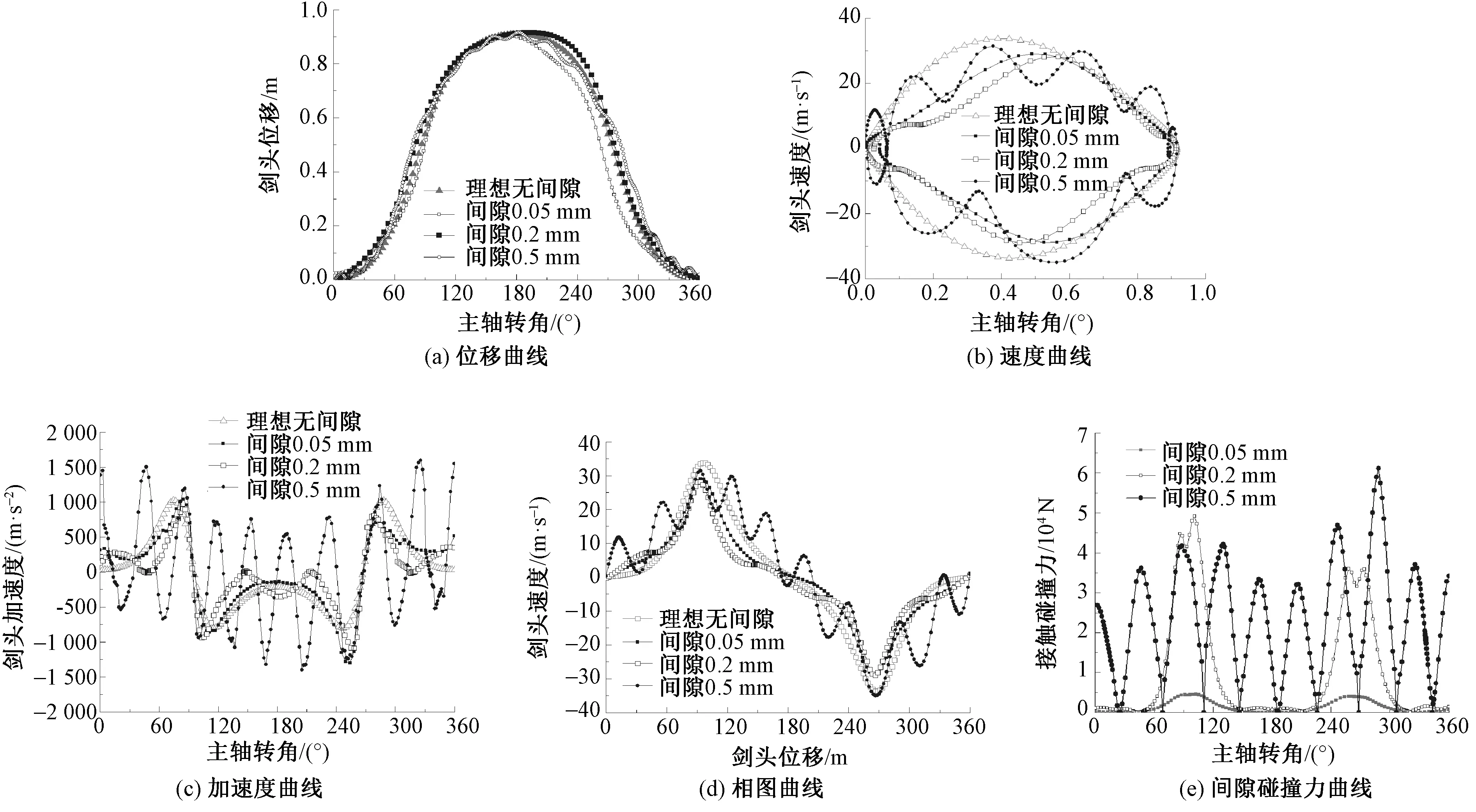
图6 不同间隙下系统的动态特性

由图6可知：间隙在0.05～0.5 mm范围内变化时，对于剑头位移的峰值影响是相对较小的；当间隙大于0.2 mm以后，剑头速度在整个运动周期内呈现较大幅度波动，参照系统相图可知，在主轴转角0°～60°与300°～360°这2个区间内，剑头速度波动频率相对较高，运动规律中“快进”和“急回”特性的稳定性受到削弱，这将对织机重新拾取纱线并再次进入梭口带来不利影响；间隙对于剑头加速度的作用是最大的。当间隙为0.05 mm时，加速度曲线波动较小。当间隙达到0.2 mm时，加速度曲线在主轴转角105°～255°区间内出现了1个较大幅度的波动，此时引纬剑头与接纬剑头正在进行纬纱交接，剑头加速度的波动会对平稳接纬带来一定程度的干扰。而当间隙继续增加至0.5 mm时，加速度曲线在整个运动周期内剧烈波动，这将会造成剑头对纱线的冲击力大幅度增加，断纬率也随之提升；最后，通过不同间隙下碰撞力的对比可知，当间隙在0.05～0.2 mm之间时，碰撞力存在2个较突出峰值，分别出现在主轴转角60°至120°和240°～300°这2个区间，结合引纬工艺可知，在剑头的送纱运动和回程过程中，含间隙运动副会出现相对较多的磨损。当间隙逐渐增大至0.5 mm时，随着碰撞的多次出现，间隙碰撞力在整个运动区间内大范围振荡，运动副磨损区域大幅增加。综上，为了保证引纬效率、织物质量和机构运行寿命，应尽可能将运动副间隙控制在0.5 mm以内。

4.2 虚拟样机检测校核及刚性铰方法对比

为校核本文动力学建模方法的准确性并讨论该方法的适用范围，建立以实测数据为基础的虚拟样机(见图7)。对虚拟样机检测数据进行采集，并与目前工程领域中常见的刚性铰建模方法进行对比。

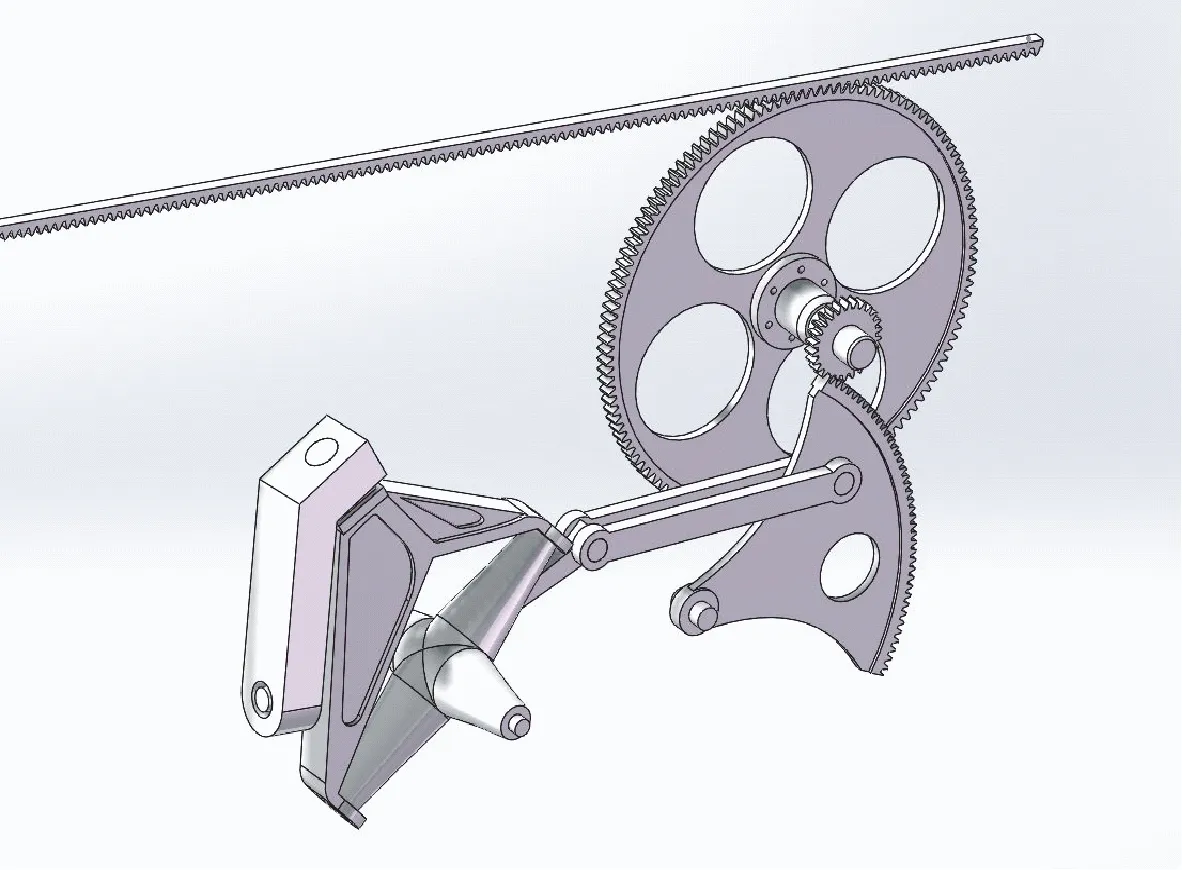
图7 空间连杆引纬机构虚拟样机

首先对速度曲线进行对比，如图8所示。在间隙为0.05 mm时，柔性铰方法、刚性铰方法和虚拟样机检测数据无论从幅值还是数值曲线的重合度都是比较高的；当间隙提高到0.2 mm时，柔性铰方法和虚拟样机检测数据的速度曲线在主轴转角120°～240°区间内出现了一定范围的波动，而刚性铰方法则呈现变化不大的小范围波动，这会导致其对于接纬过程稳定性的判断出现较大偏差；而当间隙进一步增大到0.5 mm，柔性铰方法和虚拟样机检测数据仍具有较高重合度，而刚性铰方法通过局部放大后可看到其速度曲线出现了高频率、不连续的振荡。造成上述现象的原因是刚性铰方法假定碰撞瞬间完成且轴销与轴套立即分离，没有考虑连接铰的柔性变形，因此存在速度不连续且波动幅值没有进一步提升的现象。

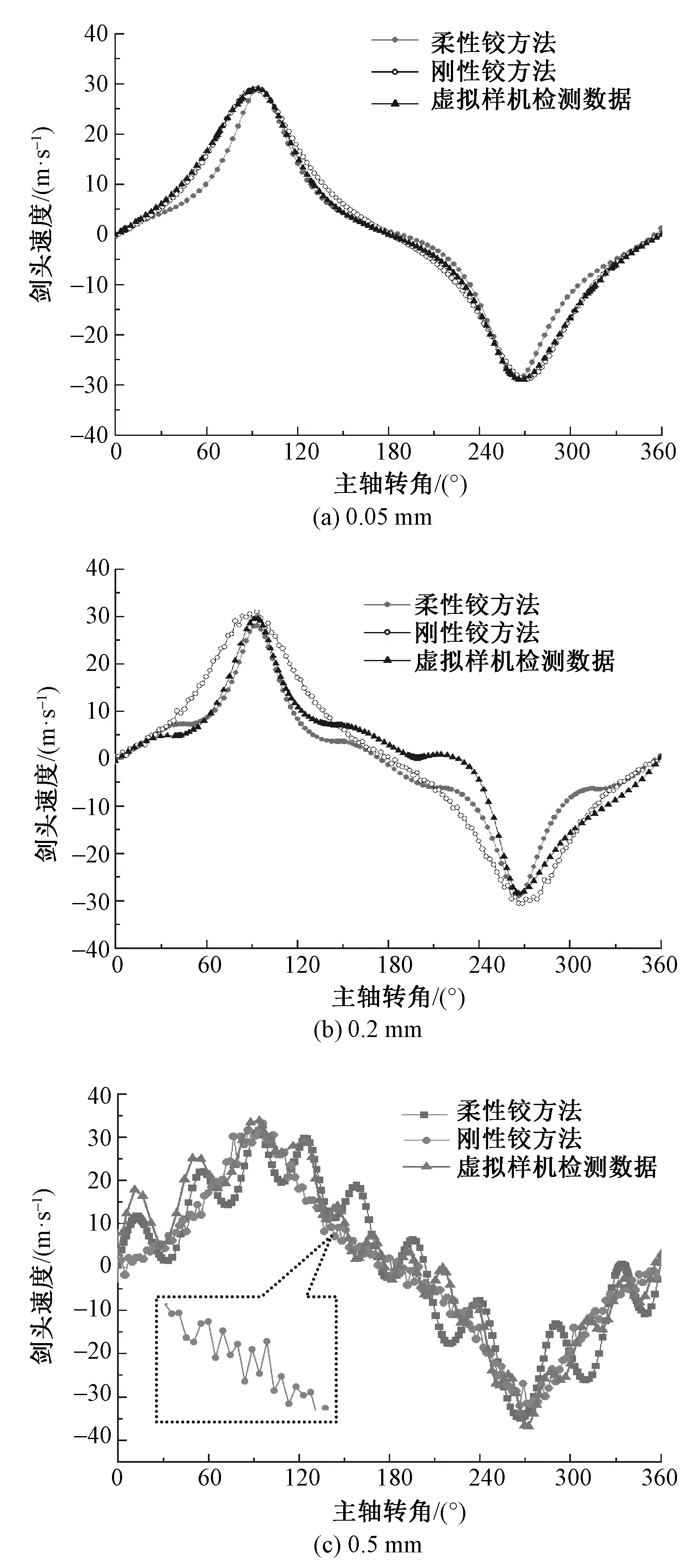
图8 不同间隙剑头速度曲线对比

其次对加速度曲线进行对比，结果如图9所示。当间隙值为0.05 mm时，柔性铰方法和刚性铰方法以及虚拟样机检测数据的曲线轨迹重合度较高；当间提高到0.2 mm及以上时，柔性铰方法和虚拟样机检测数据无论从最大幅值还是从运动轨迹上仍然保持了较高重合度，而此时的刚性铰方法则呈现全周期无规律不连续振荡，如果以刚性铰方法求解较大间隙值下的剑头加速度特性并将其作为判断引纬成功率的依据，则会出现较为明显的偏差。

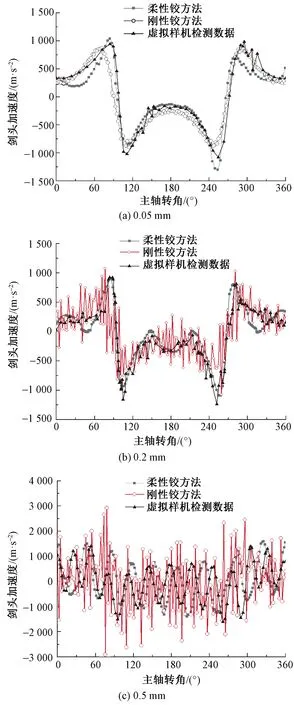
图9 不同间隙剑头加速度曲线对比

接下来，对剑头位移曲线进行对比，如图10所示。

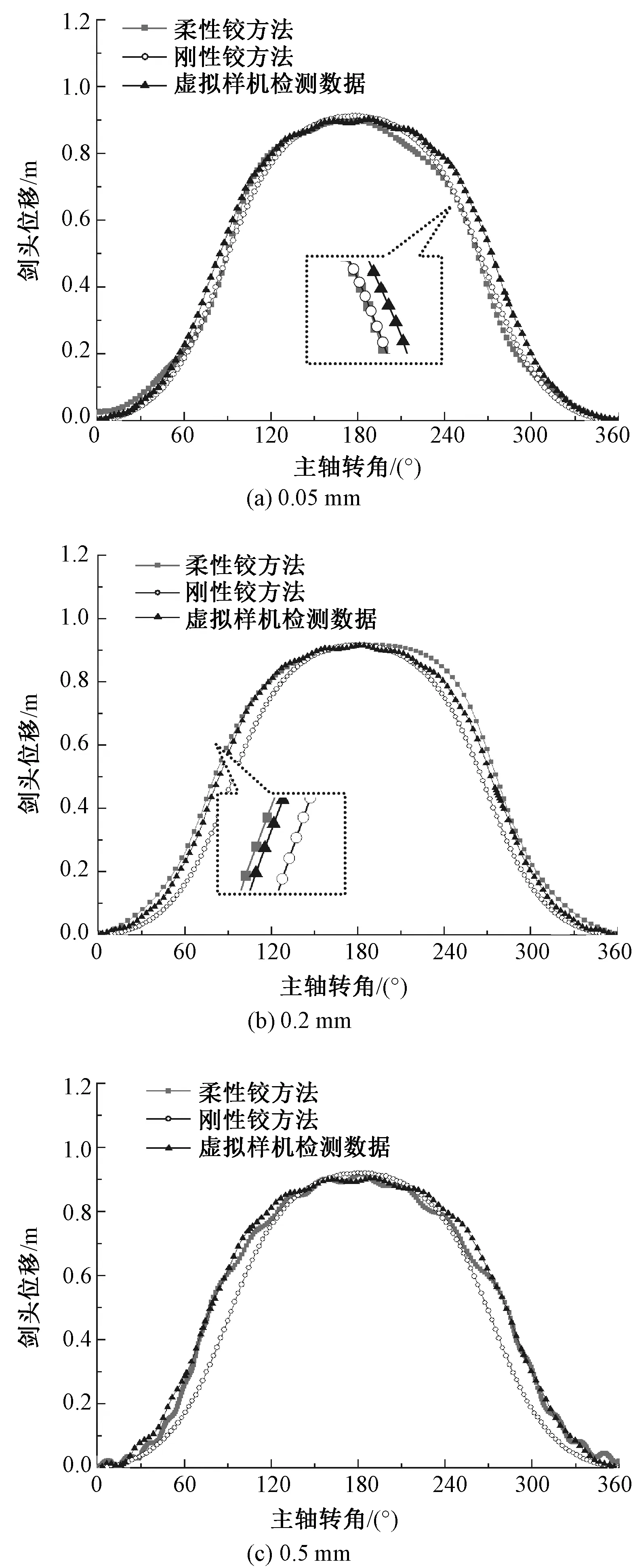
图10 不同间隙剑头位移曲线对比

在间隙值为0.05 mm的时候，刚性铰方法和柔性铰方法具有较高的重合度(见局部放大图)，2种方法的位移曲线在剑头送纱和回程阶段中与虚拟样机检测数据存在一定偏差；当间隙值继续增加到0.2 mm时，柔性铰方法与虚拟样机检测数据的曲线出现了较高的重合度(见局部放大图)，仅在主轴转角220°～265°区间内，即纬纱交接后期与回程阶段前期存在小范围偏差；当间隙值继续提升到0.5 mm时，柔性铰方法和虚拟样机检测数据的剑头位移曲线均出现了一定程度的波动，且重合度进一步提升，而此时的刚性铰方法曲线仍然较为平滑，与虚拟样机检测数据的偏差也进一步增大。

最后，对剑头位移误差幅值进行对比，如图11所示。

随着间隙值的提高，剑头位移的误差值在不断增加，且柔性铰方法与虚拟样机检测数据的曲线重合度随间隙值的增加而提升；在引纬机构运行过程中，剑头误差峰值均出现在主轴转角93.6°与266.4°左右，这2个角度分别对应纬纱开始交接与引、接纬剑头分离；在0.05 mm间隙的时候，2种方法对于误差计算的准确度相差不大，而当间隙增加至0.2 mm时，在主轴转角85.431°时，柔性铰方法的剑头误差幅值为12.76 mm，刚性铰方法为47.27 mm；在主轴转角275.618°时，柔性铰方法的剑头误差幅值是31.48 mm，刚性铰方法为102.93 mm,结果见表3所示。刚性铰剑头误差幅值分别是柔性铰的3.70倍和3.27倍。随着间隙增加到0.5 mm，柔性铰方法与虚拟样机检测数据的误差曲线呈现出相同的趋势和更高的重合度，能够更为准确地判断引纬机构在引纬运动中的稳定性。

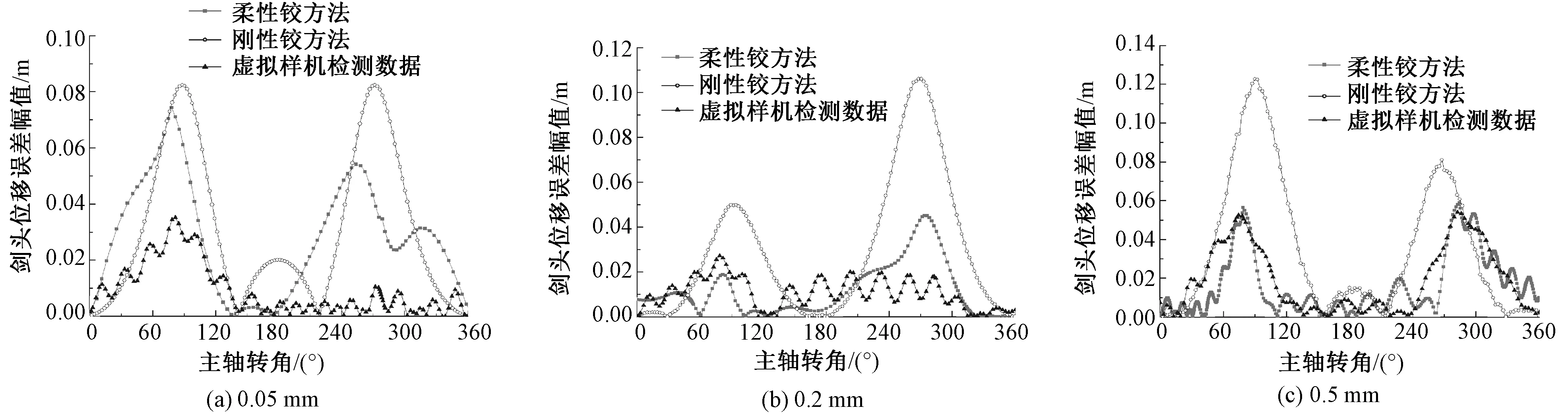
图11 不同间隙剑头位移误差幅值曲线对比

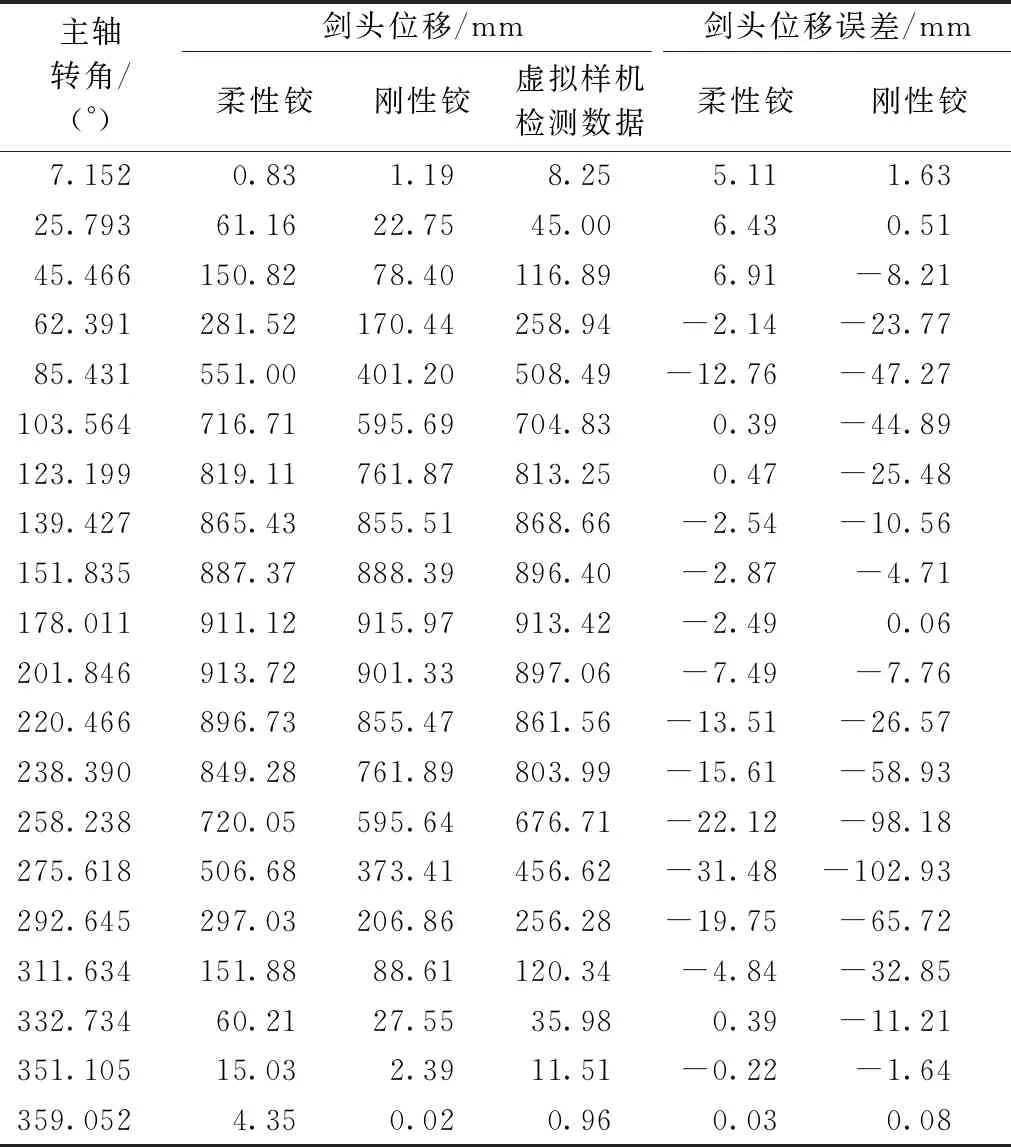
表3 剑头位移及误差对比(间隙0.2 mm)

5 结 论

本文将Lankarani-Nikravesh碰撞力模型嵌入到空间连杆引纬机构的动力学方程中，探讨间隙对于系统动态输出各项参数的影响，尤其是对于剑头位移误差的影响，对比虚拟样机检测数据，得到以下结论。

1)应用矢量法对间隙进行描述并求解机构的运动学特性，在计及柔性铰间隙作用机制的前提下，选取间隙偏心距分量和机构输出角为广义坐标，采用Newton-Euler方法建立动力学模型，模型包含间隙碰撞过程中系统的各项动态参数。

2)结合工程实例，研究间隙对引纬工艺的具体影响。当间隙持续增加时，剑头速度、加速度、接触碰撞力呈现全周期大范围波动，较为显著地影响了纬纱交接和纱线再次进入梭口过程中的稳定性。

3)通过与刚性铰方法及虚拟样机检测数据的对比，验证了本文建模方法的准确性。同时，通过分析间隙对剑头位移峰值误差的影响可知，当间隙到达0.5 mm及以上时，柔性铰方法具有更高的计算精度。