基于可调张力装置的芳纶织物交织阻力研究

陈洁如， 邱诗苑， 杨青青， 周 熠,2

(1. 武汉纺织大学 纺织科学与工程学院， 湖北 武汉 430200； 2. 武汉纺织大学 纺织纤维及制品教育部重点实验室， 湖北 武汉 430200)

现代柔性防弹衣大多是由多层织物通过吸收和耗散发射体的动能来阻止高速射入的子弹。Bazhenov[1]认为织物防弹性能与抽拔纱线的数量有关。Nilakantan等[2]研究了子弹射入期间织物的侵彻率发现，纱线抽拔对子弹能量耗散起主要作用。

纱线抽拔是指单根纱线在外力作用下从织物结构中被抽出。抽拔力的大小与织物的结构形状、纱线交织交叉点的摩擦性能相关[3]。交织阻力是指织物在组织点处经纬纱之间的摩擦力，即纱线在组织结构中因为摩擦和形变作用，抵御抽拔的能力。在纱线抽拔过程中所需的作用力与织物间纱线摩擦阻力值是对等的，如同作用力和反作用力一样。从本质上来说，纱线抽拔是经纬纱之间的相互摩擦作用。虽然纤维之间的摩擦因数可通过测试获得，但即便所用纤维完全相同，织物内纱线间的交织阻力也会因织物的纬向宽度、织物的经向宽度、对织物施加的横向预加张力的差异而不同。

织物在受到弹道冲击时,织物中纱线的抽拔滑移是一种重要的吸能方式[4]。研究高性能织物在纱线抽拔过程中的准静态以及动态响应，有利于为进一步优化设计防弹服提供新的理论指导。尽管国内外研究者已经在此领域做出突破[5]，但是多数实验没能处理好子弹射入时对纱线产生的预加张力。对于具体预加张力数值的调节与稳定成为研究纱线抽拔过程与防弹衣分析建模难以突破的障碍。研究者Zhu等[6]所做的412 N和208 N的预加张力实验已经发现，将预加张力调到特定数值并使其稳定的困难性。

织物是一种柔性体,在抽拔中既要保证受到抽拔的纱线能够顺利抽出,又要整个织物保持平整且被握持的状态,才能真实模拟织物在受到冲击过程中的状态。目前的织物拉伸夹具都是针对整个织物一端进行整体夹持,没有既能有效握持织物又能顺利抽拔出单根纱线的抽拔装置[7]。

为解决现有技术中存在的问题,本文将使用一种自主设计的可调预加张力的纱线抽拔装置,通过YG028万能材料实验机得出抽拔实验中纱线的交织阻力-位移曲线，研究芳纶织物纱线在不同规格尺寸、不同预加张力条件下对交织阻力的影响。同时构建一个模型公式，用以预测对于不同规格尺寸、不同预加张力情况下纱线抽拔所产生的交织阻力值。

1 实验部分

1.1 材料与仪器

材料：Kevlar-29芳纶平纹织物，经纬向密度均为70根/(10 cm)，经纬纱线密度均为1 667 dtex，美国杜邦公司。

仪器：YG028型万能材料实验机(温州方圆仪器有限公司)；可调横向预加张力装置(自主研发)。图1示出可调横向预加张力的织物夹具。包括底座、安装框(含光滑槽口)、左右夹钳、压力传感器、螺栓以及弹簧。其中,左夹钳为固定夹钳，用来固定织物的一端。右夹钳则为活动夹钳，可以沿横向平行移动。主框架上下两侧都开有可供右钳平移的光滑槽口。

①—左夹钳；②—安装框；③—纱尾；④—右夹钳；⑤—传感器；⑥—带弹簧的螺栓；⑦—光滑槽口；⑧—夹具底座。

1.2 实验方法

参照GB/T 3923.1—2013《纺织品 织物拉伸性能 第1部分:断裂强力和断裂伸长率的测定(条样法)》,使用万能材料实验机进行试样纬纱的抽拔实验，上夹头的拉伸速度设定为100 mm/min，拉伸实验机隔距为200 mm。

将织物试样分别裁剪成8 cm×8cm、13 cm×8 cm,18 cm×8 cm(此3种试样纬向宽度均为8 cm，仅改变经向宽度值)，以及13 cm×4 cm,13 cm×8 cm,13 cm×12 cm(此3种试样径向宽度均为13 cm，仅改变纬向宽度值)。实验过程中，将织物两侧固定在左右夹钳，通过控制调整螺栓对传感器的压力来改变织物的横向张力(仅用螺栓顶住传感器，织物会很快产生应力松弛现象[8]，而在螺栓处添加一个弹簧能使织物张力在短时间内保持稳定)。

通过图1所示夹具给予试样不同的预加张力，测试织物交织阻力以及横向张力变化情况。为提高实验结果的准确性，每组实验选取4个平行样品进行测试。本文实验在测试之前需从织物的顶部边缘手动移除经纱以露出40 mm的纵向纬纱纱尾。

2 结果与讨论

2.1 抽拔曲线特性分析

图2示出了织物交织阻力以及横向张力与被抽拔纱线纵向位移关系图。其中交织阻力曲线记录了拉伸实验机上夹头传感器所受长丝束交织阻力的变化状态，横向张力曲线记录了横向传感器所受横向张力的变化状态。(在大量的实验数据中，因不同的预加张力条件下得出的曲线图变化趋势基本一致，故在此仅选取出13 cm×12 cm织物在400 N预加张力下的实验曲线为分析对象)。

图2 织物交织阻力以及横向张力与被抽拔纱线纵向位移关系图

交织阻力曲线示出，长丝束所受交织阻力在初始阶段达到峰值后，继而呈现一种振荡递减的变化规律。横向张力曲线和交织阻力曲线所体现的变化规律基本上一致。这种规律反映了平纹结构在抽拔过程中的准静态响应。长丝束在被抽拔时，会给予横向经纱一个垂直方向的拉伸力，使得经纱屈曲逐渐变大，进而导致横向张力有所增大。与此同时所需抽拔力也相应增大，即长丝束所受交织阻力增大。直至长丝束移出一个交织点，经纱受力点相应减少，致使横向张力又略有下降，纬向所需抽拔力也发生略微减少。在抽拔过程中反复经过和移出一个又一个交织点，故交织阻力曲线和横向张力曲线均出现振荡递减趋势[5]。利用铰链模型模拟交织点的受力状态，科学分析了张力的这种振荡变化趋势。纬纱和经纱处于啮合态时，经纬纱形变恢复，横向张力也由此减小，纱线抽拔力处于谷值，反之亦反。这也解释了图2中横向张力曲线与交织阻力曲线的波峰与波谷一一对应的原因。当长丝束被彻底抽出后，纬向给予横向经纱的拉伸力消失，同时横向经纱和纬纱的交织点也处于最小点数，故如表1所示，最终横向张力比较于初始预加张力发生减少。

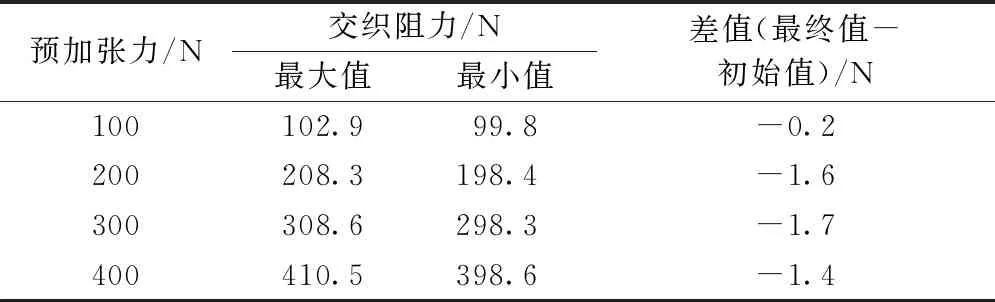
表1 13 cm×12 cm织物在不同预加张力下交织阻力的最值

2.2 预加张力对抽拔曲线的影响

图3示出试样在不同的横向预加张力下长丝束所体现出的交织阻力-位移曲线。可知，不同预加张力作用下单纱抽拔实验的交织阻力变化规律基本一致，都存在退屈曲区和黏滑区。研究发现，最大交织阻力与横向预加张力之间的变化呈正相关性，而且两者之间的涨幅呈对数关系。100、200、300和400 N的预加张力下测得的最大交织阻力分别为6.45、9.1、11.08、12.41 N，相邻阶段张力增幅分别为41%、21.7%、12%。可见最大交织阻力增幅越来越小。原因可能是增加横向纱线的张力增加了纱线之间的法向力，进而增加了纱线抽拔的摩擦阻力，故需要较大增量的抽拔力才能使长丝束被抽拔出。织物受到的横向张力越大，经纬纱的屈曲交换则更加不容易实现，因此在达到最大交织阻力之前，曲线模量略有升高。再者根据绞盘方程T=T0eμθ(见图4)，给定输入张力T0,输出张力T由纱线和圆柱面间的摩擦因数μ以及接触角θ决定。在屈曲交换越艰难的情况下，被抽拔的长丝束与横向经纱的接触角θ越大，则输出张力T增大，即长丝束所受到的最大交织阻力增大[9]。

图3 8 cm×8 cm平纹机织物抽拔实验交织阻力-位移曲线

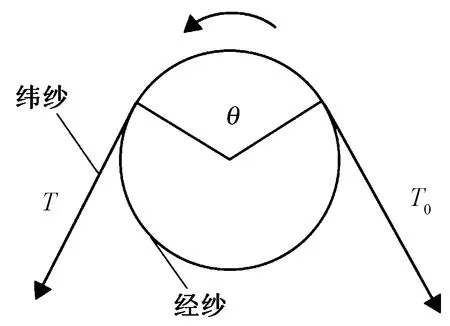
图4 绞盘方程的示意图

2.3 织物经向宽度对交织阻力曲线的影响

图5示出在400 N预加张力下织物经向宽度的改变对交织阻力的影响。可知，织物经向宽度越宽，长丝束被抽拔时所受的最大交织阻力越小，其抽拔曲线的初始模量也越小。在预加张力不变的情况下，随着织物经向宽度的增加，经纱屈曲部分的伸直以及自身伸长变形的横向空间均会增加，这将有利于经纱屈曲变大，同时也有利于纬纱的伸直，使得纱线的屈曲交换变得更为容易，故曲线的初始模量变小。再者根据绞盘方程，在屈曲交换变得更为容易的情况下，被抽拔的长丝束与横向经纱的接触角θ减小，故输出张力T减小，即长丝束所受到的最大交织阻力减小。

图5 400 N预加张力下不同经向宽度织物的交织阻力曲线

图6示出预加张力分别为100、200、300、400时产生的最大交织阻力值。结果表明,宽度为8、13、18 cm试样，预加张力从100 N增至400 N时，增幅分别为98.33%、78.28%、62.15%。当预加张力逐渐增大时，织物经向宽度对交织阻力的影响逐渐增强。因为依据前文分析，当预加张力增大时，纱线屈曲交换变得更艰难，进而纱线抽拔时的交织阻力变大。与此同时，预加张力不变时，经向宽度越宽，则纱线被拉伸时可伸长的长度距离更大，越有利于屈曲交换。故而所需交织阻力越小。预加张力和经向宽度的增加对于抽拔纱线张力的影响正好是相反的，而相比较于经向宽度的影响，预加张力对于抽拔力的影响显得更为突出，故呈现出此种情况。

图6 不同预加张力下不同经向宽度织物最大交织阻力对比图

2.4 织物纬向宽度对交织阻力曲线的影响

不同纬向宽度织物对交织阻力影响的对比如图7所示。可知，随着织物纬向宽度的增大，长丝束所受的交织阻力呈指数增长。预加张力为100和200 N时，最大交织阻力产生时发生的位移随着织物纬向宽度的增加而增加，但当预加张力为200、300和400 N时，最大交织阻力发生时的位移随着织物长度的增加呈非线性增加。织物纬向宽度的增加导致了接触面积的增加，从而增加了纱线抽拔时的摩擦阻力，此外随着织物纬向宽度的增加，交织点的数量也相应增加，导致长丝束路径弯曲度增加，故长丝束被抽拔时所消耗的能量也随着织物纬向宽度的增加而呈指数增长。

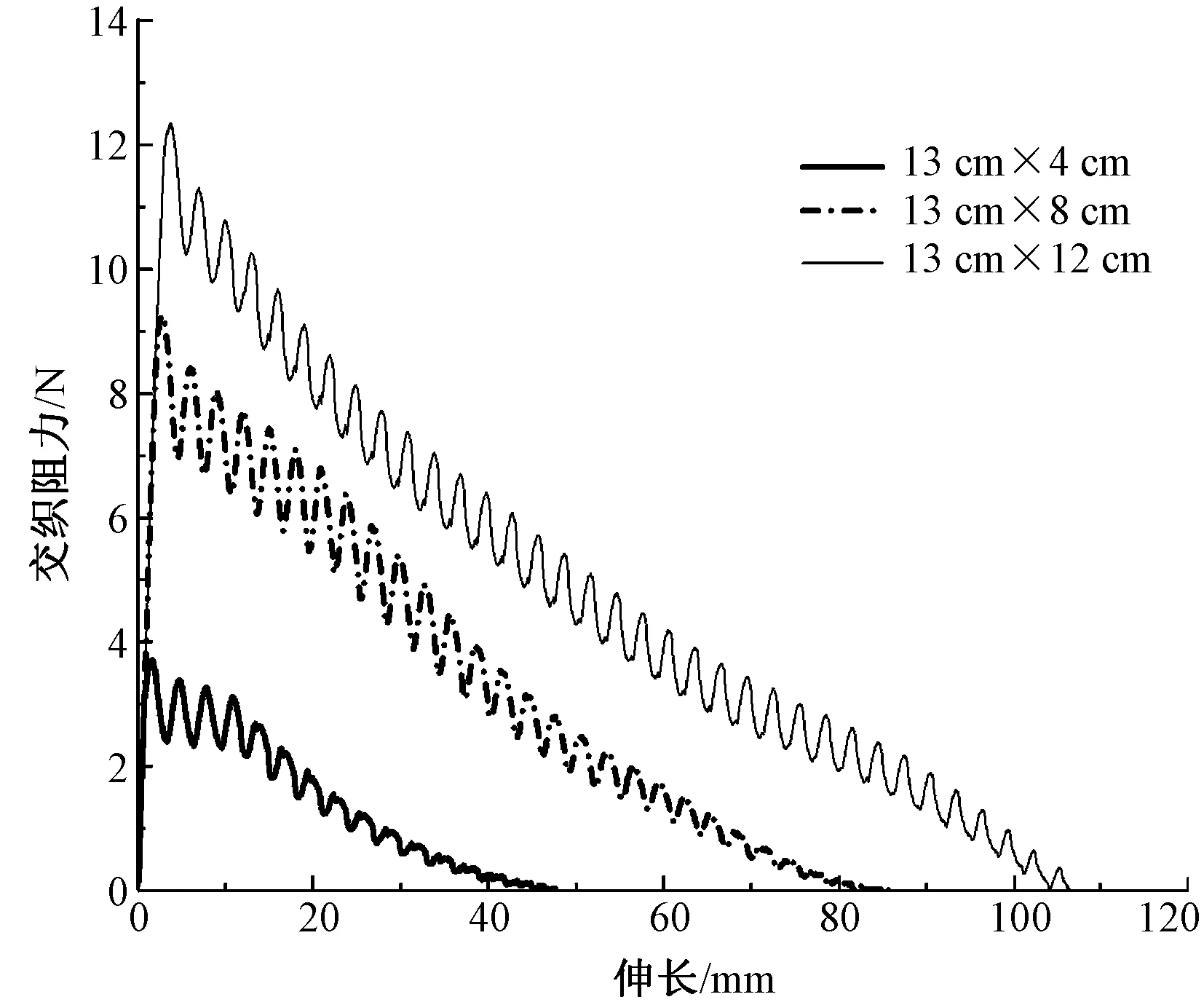
图7 300 N预加张力下不同纬向宽度织物的交织阻力曲线

图8示出预加张力分别为100、200、300、400 N时产生的最大交织阻力值。可知，当预加张力为100 N时，对比纬向宽度为4和8 cm，以及8和12 cm，均是随着纬向宽度的增加，其最大交织阻力明显增大，但增长百分比却大为不同。前者增长百分比为104%，后者为36.6%；预加张力为200 N时，前者为119.6%，后者为44.9%；预加张力为300 N时，前者为140.9%，后者为50.43%；预加张力为400 N时，前者为157.27%，后者为47.17%。由此可见，预加张力一定时，织物纬向宽度呈比例增加时，最大交织阻力逐渐增大，但增幅呈递减趋势。预加张力逐渐增大时，织物纬向宽度对交织阻力的影响逐渐增强。

图8 不同预加张力下不同纬向宽度织物最大交织阻力对比图

3 交织阻力模型

3.1 模型公式构建

预构建一个模型公式，用以预测不同经向宽度、不同纬向宽度、不同预加张力情况下抽拔纱线所产生的交织阻力的数值。首先选用半经验公式法对抽拔实验的结果进行参数化设定。

3.1.1 退屈曲区模型

当上夹头对纬纱施加外力后，纱线张力迅速到达一个峰值，在交织阻力-位移曲线上，这一区域称为“退屈曲区”[10]。

对于每一测试样品，分别根据其测得的峰值抽拔力Fp和峰值位移Xp对退屈曲区的力和位移数据进行归一化。该归一化数据可以通过以下公式进行建模。

(1)

式中：F为抽拔拉力，N；Fp为最大抽拔拉力，N；X为试样被抽拔时移动的位移，mm；Xp为抽拔力达到最大值时试样产生的位移，mm；α为关系系数。

可以通过MatLab中非线性最小二乘法为数据集计算出最合适的α值为0.749。其拟合优度(R2)值达到0.988。

然后将每个数据集的实验数据Fp和Xp值与方程拟合。各自方程式分别为:

Fp=a1+a2L1+a3L2+a4T+a5L1T+a6L2T+a7L1L2+a8L1L2T

(2)

Xp=b1+b2L1+b3L2+b4T+b5L1T+b6L2T+b7L1L2+b8L1L2T

(3)

式中：L1为试样经向宽度，mm；L2为试样纬向宽度，mm；T为预加张力，N;常数a1、a2、a3、a4、a5、a6、a7、a8,以及b1、b2、b3、b4、b5、b6、b7、b8可以通过MatLab软件编程并代入已测得的实验数据，运用非线性最小二乘法求解得出。

3.1.2 黏滑区模型

在“黏滑区”内，随着位移的增大，交织阻力呈现出一种振荡衰减趋势。对于这个阶段的每个数据集，同样可分别通过测得的峰值抽拔力Fp和峰值位移Xp数据来进行归一化。该归一化数据可以通过下式进行建模。

(4)

结合公式(2)、(3)，通过MatLab运用非线性最小二乘法为数据集计算出最合适的λ1、λ2值，分别为8.822、0.658。其拟合优度(R2)值为0.973，说明拟合效果很好。

3.2 模型评估

通过交织阻力-位移曲线的完整模型公式，结合已得的实验数据绘制出了一个完整的拟合曲线，见图9所示。在整个实验条件范围内，模型的拟合优度(R2)值达到0.973。这一点从拟合图中可得到的很好地印证，可看出拟合效果非常好，半经验模型准确地代表了实验数据。

4 结 论

本文研究了芳纶织物在不同规格尺寸、不同预加张力条件下进行单纱抽拔对交织阻力的影响，得出以下主要结论。

1)织物所受预加张力越大，经纬纱的屈曲交换越不容易实现，则输出张力增大，长丝束所受到的最大交织阻力增大。

2)织物经向宽度越宽，则纱线被拉伸时屈曲部分的伸直以及自身伸长变形的横向空间均会增加，越有利于屈曲交换，故而所产生的交织阻力越小。

3)织物纬向宽度越宽，则纱线被拉伸时接触面积更大，交织点的数量也更多，从而增加了纱线抽拔时的摩擦阻力，即所产生的交织阻力越大。

织物所受交织阻力可评价织物的剪切变形性，在一定程度上可体现高性能纤维织物的防弹性能。同等条件下，织物交织阻力越大，越有利于织物的防弹性能的提高。通过研究芳纶织物的交织阻力影响因素，可为进一步优化设计防弹服提供理论指导。交织阻力半经验模型公式可使实验人员快速获取织物在单纱抽拔时的交织阻力值，在很大程度上提高了实验效率。