棉精梳机钳板机构开闭口分度分析及仿真研究

王延蒙，纪 红

(济宁职业技术学院，山东 济宁 272073)

0 引言

在棉精梳工艺过程中，钳板机构握持须丛供锡林梳理，并将锡林梳理好的须丛送向分离罗拉。精梳机高速运转时，钳板的开口分度、闭口定时及闭合分度的长短对精梳条质量有重要影响[1]。

目前，对精梳机钳板机构的研究主要有：黄华等基于ADAMS对精梳机钳板机构进行优化设计[2]；贾国欣等对瑞士立达棉精梳机的钳板机构进行运动学分析，讨论了影响钳板开口量的因素，并对钳板运动的振动进行优化[3-4]；王晓维在不改变工艺参数的情况下，利用伺服电机改变输入规律减少钳板机构的振动情况[5]。以上研究均未对钳板机构的开闭口定时分度进行详细分析。

为此，笔者利用运动学矢量方法分析钳板开口机构，建立其开闭口时间及开闭合分度与机构参数关系的数学模型，通过三维虚拟样机模型导入ADAMS进行仿真，得到开口时间和设想杆长度的变化关系，精确计算出开闭口定时分度及开口时间，以提高精梳质量。

1 棉精梳机钳板开口机构

精梳机钳板开口机构简图如图1所示。钳板开口机构为二自由的七连杆机构，笔者根据钳板开口机构工作状态简化为双摆杆机构和偏心机构，将偏心轮、皮老虎、偏心导杆等同于设想杆[6]。以设想杆长度作为研究变量，使用运动学矢量分析方法计算钳板开口机构各参数之间的定量关系。

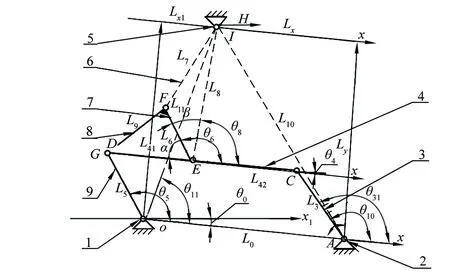
1—输入轴；2—钳板摆轴；3—后摆臂；4—下钳板；5—偏心轴；6—虚拟杆；7—上钳板架；8—上钳板；9—前摆臂。

以输入轴和钳板摆轴连线记作x方向，其距离为L0；前摆臂长度为L5，与x方向的夹角为θ5；后摆臂长度为L3，与x方向的夹角为θ31；下钳板长度为L4，与x方向的夹角为θ4；下钳板以铰接点为界又分为L41和L42；上钳板架长度为L6；EH长度为L8，与x轴的夹角为θ8；AH长度为L10，与x方向的夹角为θ10；OH长度为L11，与x方向的夹角为θ11；A，H两点x方向距离为Lx，垂直距离为Ly；O，H两点的x方向距离为Lx1，垂直距离为Ly1；∠FEH为β；∠FED为α；x方向与水平轴x1的夹角为θ0。

1.1 简化钳板开口机构分析

1.1.1 计算θ8

在图1中ACEH在各矢量的方向上有：

(1)

在x，y两轴上分解，得：

(2)

整理可得：

θ8=π+

(3)

1.1.2 计算θ4

OACD在各矢量的方向上有：

L5eiθ5+L4eiθ4=L0+L3eiθ31

(4)

在x，y两轴上分解，得：

(5)

消去θ5得θ4与θ31的关系：

L02+L42+L32-L52-2L0L4cosθ4+2L0L3cosθ31-2L3L4cos(θ31-θ4)=0

(6)

消去θ4得θ5与θ31的关系：

L52+L32+L02-L42=2L5L3cos(θ31-θ5)+2L5L0cosθ5-2L3L0cosθ31

(7)

1.1.3 计算β

ODEH在各矢量的方向上有：

(8)

在x，y两轴上分解，得：

(9)

消去θ8得：

L82=L52+L412+Lx2+Ly2-2LxL5cosθ5-2LxL41cosθ4-2LyL5sinθ5-2LyL41sinθ4+2L5L41cos(θ5-θ4)

(10)

在ΔEFH中，可得：

(11)

角α，β，θ8，θ4的关系可以表示为：

α+β+θ8-θ4=π

(12)

综合公式(3)，(6)和(11),即将β，θ8和θ4代入式(12)可得θ31与L7的关系。

1.2 钳板开口分度分析

如图2所示，Lf为分离罗拉与下钳板的水平距离，Lm为分离罗拉与输入轴的水平距离，根据几何关系：

1—锡林轴；2—钳板摆轴；3—钳板后摆臂；4—下钳板；5—钳板前摆臂；6—分离胶辊；7—分离罗拉。

Lf=Lm-L5cos(π-θ5+θ0)

(13)

整理得：

(14)

设钳板在24分度时，钳板摆轴角位移等于θ3q，锡林轴的角位移等于θ1q；钳板开口瞬时分度，钳板摆轴的角位移等于θ3k，钳板后摆臂与x轴的夹角记为θ31k；24分度时，钳板后摆臂与x轴的夹角为θ31q，锡林轴的角位移等于θ1k；钳板闭口瞬时，钳板摆轴的角位移等于θ3b，钳板后摆臂与x轴的夹角记为θ31b，锡林轴的角位移等于θ1b。由几何关系可得：

θ1q=2π-arccos(L1/L0)

(15)

(16)

θ3k=θ3q-(θ31q-θ31k)

(17)

θ3b=θ3q-(θ31q-θ31b)

(18)

结合式(2)和式(3)得：

(19)

(20)

2 仿真验证

以立达E62型精梳机为例：L0为207 mm，L1为65 mm，L3为82 mm，L4为187 mm，L41为75 mm，L42为112 mm，L5为74 mm，L6为72 mm，L9为74 mm，Lx为147.1 mm，Ly为211.65 mm，Lx1为59.3 mm，Ly1为211.65 mm，Lm为53.9 mm，θ0为8°，落棉隔距B的范围为19 mm～26 mm。首先利用Pro/E软件建立钳板开口机构三维模型，如图3所示。将该模型保存为x-t格式导入ADAMS软件。根据其自由度数设置两台伺服电机驱动，建立转动副约束和移动副约束。

图3 Pro/E三维机构建模图

设定精梳机工作转速为400 r/min，1个工作周期为0.15 s，将仿真时间也设置为0.15 s。在ADAMS环境下的模拟结果如图4所示。

图4 虚拟样机模拟图

将钳板输入轴运动规律输入到伺服电机中，进行运动学仿真分析，利用ADAMS/PostProcessor模块输出设想杆长度L7与运行时间t的仿真关系曲线，如图5所示。

由图5可知：在一个工作周期内设想杆L7在开始时刻和结束时刻长度值最大，约为111.8 mm，长度最小时L7min为94.01 mm；当L7为103 mm时是钳板开口瞬时时刻和闭口瞬时时刻，钳板开口定时时刻tk为0.0844 s、闭口定时的时刻tb为0.028 6 s；在开、闭口瞬时时刻设想杆长度越长，钳板开口定时时刻会越早，钳板闭口定时会延迟。

图5 钳板运行时间t与设想杆长度L7的关系

把上文中列出的公式输入MATLAB中，进行精梳机钳板机构参数计算，得到钳板开口机构的开口时刻为0.087 5 s、闭口时刻为0.030 s。由于在ADAMS环境下，钳板机构虚拟模型不可避免的存在装配误差，所以ADAMS仿真结果存在一定误差。为得到钳板开闭口分度值，用公式(21)将钳板开口定时时刻tk和闭口定时时刻tb进行转化，得到钳板开口机构开闭口分度表。其中Fk，Fb为钳板开口和闭合的输入轴分度数，T为输入轴旋转1周的时间，结果见表1。

(21)

3 结论

3.1钳板开闭口机构的开口定时、闭口定时及开闭口分度影响锡林梳理、分离结合等后续工艺，利用运动学方法建立开闭口分度与机构参数之间的数学模型，通过仿真验证钳板机构开闭口定时分度及开闭口时间与设想杆长度的关系。在开闭口瞬时时刻，开口定时分度为6.587 9、闭口定时分度为32.436；在开闭口瞬时时刻随设想杆长度增加，开口定时分度会变早，闭口定时分度会推迟。

表1 钳板运动关键位置点计算结果对比

3.2利用钳板机构开闭口数学模型可以进一步研究其他参数对开闭口分度的影响，为提高精梳机精梳质量提供参考。