基于强边缘和稀疏约束的运动模糊图像盲复原∗

鱼 轮 李晖晖

（1.商洛学院电子信息与电气工程学院 商洛 726000）（2.西北工业大学自动化学院信息融合技术教育部重点实验室 西安 710129）

1 引言

在获取图像的过程中，由于噪声等外界环境因素干扰，成像设备与目标物体之间的相对位移，会导致物体成像信息丢失变得模糊。运动模糊图像复原的目标，就是要从模糊图像中恢复出原始的清晰图像。由于实际观测活动中，点扩散函数（Point Spread Function，PSF）的变化规律是未知的，因此常用的图像复原方法是盲复原法，该方法在使用时会对模糊图像做适当的约束，然后再结合PSF的约束条件，推导最优估计准则，这类方法包括IBD（Itera⁃tive Blind Deconvolution）算法［1］，空间正则化算法［2］等经典复原算法。IBD算法是一种在空域和频域交替数值迭代的盲解卷积算法，复原速度较快，但是对噪声敏感，收敛性不能保证。正则化算法的关键是寻找合适的正则约束项，当正则约束惩罚项找到后，结合最小化准则项，就可以形成一个易于求解的代价函数。近几年，基于稀疏正则项约束的图像复原得到了广泛的应用，该方法认为清晰自然图像的边缘和模糊图像的边缘分布有差异，Fergus等［3］采用高斯混合模型来约束图像的梯度分布，但该算法在近似饱和的区域存在较大的振铃效应。Shan等［4］对图像噪声的空间随机分布模型进行重建，采用分段函数拟合具有指数分布特征的点扩散函数分布，Krishnan等［5］采用超拉普拉斯分布来近似图像的梯度分布，然而以上算法在处理模糊图像时，模糊图像中的无效边缘、弱边缘和伪边缘会错误指导估计模糊核，导致复原结果变差。

针对上述问题，本文受文献［6～7］启发，提出一种基于强边缘和稀疏约束的运动模糊图像盲复原，首先利用双边滤波器和冲击滤波器分别对模糊图像进行保边去噪和强化边缘处理，然后对点扩散函数施加稀疏约束和能量约束，循环迭代求解代价函数方程，算法收敛时，得到最终估计图像。

2 运动模糊图像复原模型

运动模糊图像的图像复原模型，可以看做是一个线性时不变系统，用方程式表述为g=k⊗u+n。式中，g、u分别为模糊图像、清晰图像，k和n分别为点扩散函数和加性噪声，符号⊗表示卷积。

3 基于强边缘和稀疏约束的运动模糊图像盲复原算法

3.1 算法概述

为了准确估计点扩散函数，本文算法首先对输入的模糊图像进行多尺度分级，在每一级尺度提取图像的强边缘，对图像施加稀疏约束，对点扩散函数施加能量约束，然后将当前尺度估计的复原图像作为下一个尺度的输入图像，循环迭代，当达到最大尺度时，得到最终估计的复原图像。算法流程图如图1所示。

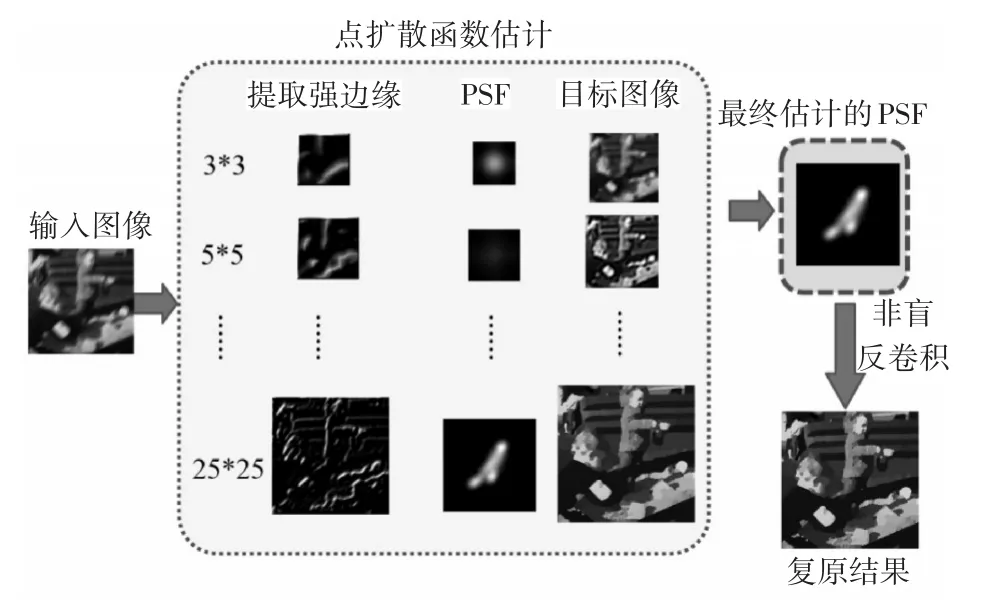
图1 算法主程序流程图

3.2 提取强边缘

在提取强边缘阶段，本文对输入的模糊图像依次使用双边滤波器和冲击滤波器处理，以达到保边去噪和强化边缘的目的。

为消除使用滤波器带来的噪声扩大问题，将图像转到梯度域进行梯度筛选，设置梯度阈值剔除掉无效的边缘，这样就可以得到强边缘。提取强边缘的算法流程如图2所示。

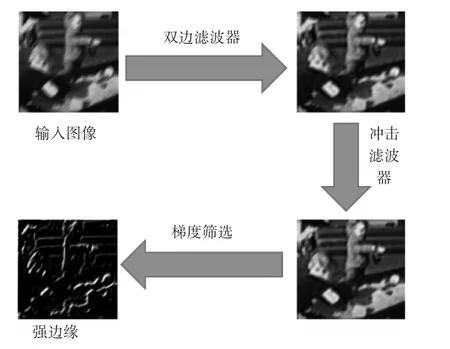
图2 提取强边缘的算法流程图

文献［7］中作者Krishnan在研究复杂街景图像模糊程度与范数间关系时指出，用范数做约束，会更容易得到最优解［7］。本文借鉴文献［7］的思路，对图像施加稀疏性约束，提出的基于强边缘和稀疏约束的运动模糊图像盲复原算法的梯度域代价函数为

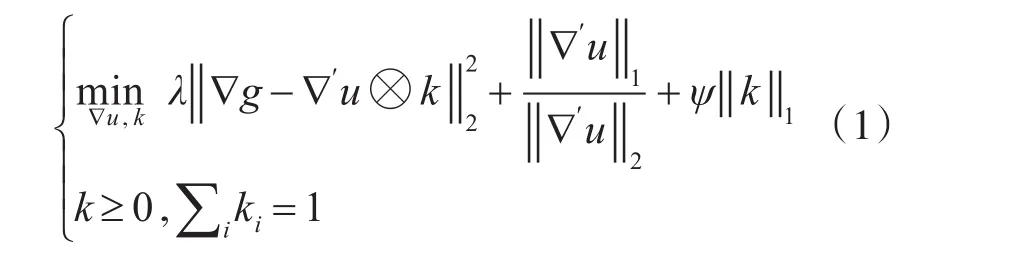
式中，第1项为保真项，用于衡量估计误差，第2项为施加在图像上的比值稀疏性约束，用于指导图像复原，第3项为模糊核约束项，用于约束模糊核估计中产生的噪声，∇′u表示提取的强边缘，λ和ψ表示权重，为方便描述，令y=∇g，x=∇′u，h=k，则上式可改写为

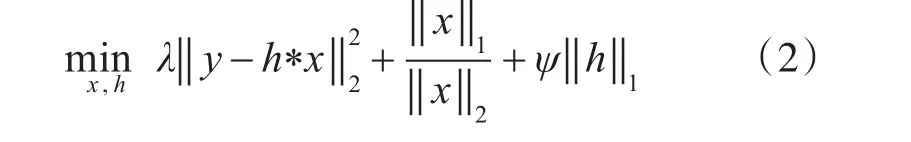
上式是一个非凸问题，本文将代价函数拆分为目标图像的估计和点扩散函数的估计两个子问题，交替循环迭代最小化，当满足迭代终止条件时，得到最终估计的点扩散函数。

3.3 目标图像的估计

估计目标图像时，将上次迭代的点扩散函数作为已知量用͂表示，代价函数为

式中，͂是的矩阵形式，式（3）中只有x一个变量，由于方程含有l1l2范数约束是非凸约束，因此固定分母为上一次迭代的结果，此时方程变为l1约束问题，采用迭代阈值收缩算法［8］对上式进行求解。

考虑到交替迭代求解x和h的过程中，分母‖x‖2会发生变化进而影响在代价函数中的权重，因此设置内外两层循环，内循环用迭代阈值收缩算法求解x，外循环更新权重参数，具体的目标图像估计算法实现步骤如表1所示。

表1 目标图像的估计算法实现步骤

3.4 点扩散函数的估计

估计点扩散函数h的时候，将上次更新的图像表示为已知量，代价函数为

式中，͂是͂的矩阵形式，方程是一个l1范数优化问题，选用收敛速度较快的迭代重加权最小均方误差算法［9］对其求解，近似代价函数为

J(h)的最优解为

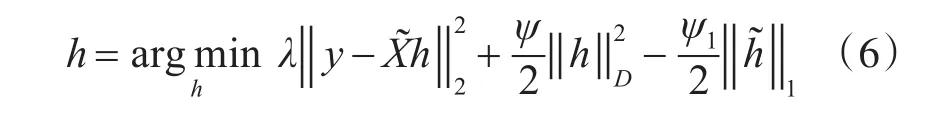
求导后，得：

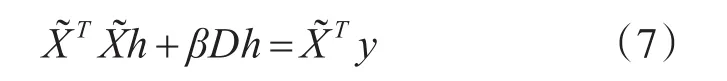
其中β=ψ/λ，上式是Ah=b的形式，采用共轭梯度法［10］进行求解。

下面给出估计点扩散函数的具体求解全过程。

输入：上次迭代更新的点扩散函数作为h的初始值，图像取本次更新的强边缘的值作为常量，最大迭代次数N为10，当前迭代次数k最大设为8，初始值为0，迭代停止误差ε为10-4，β取0.01。

3.5 非盲复原

当点扩散函数h估计出来之后，选择文献［5］中的非盲复原算法对模糊图像进行复原，代价函数为

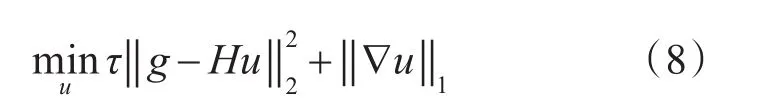
式中，τ表示权重参数，上式求得的u是当前估计的复原图像，同时也是下一次迭代中提取强边缘阶段的输入。重复以上三个步骤，直到满足最终的迭代截止条件，就可以得到复原图像。

4 仿真结果与分析

为验证文中方法的有效性，做了两组对比性实验。第1组选取了文献［11］Levin提供的公开运动模糊数据集进行测试，第2组选取一张真实场景下的人脸模糊图像进行测试，对比的方法都是图像盲复原领域中较为先进的方法。客观评价指标选用峰值信噪比PSNR、拉普拉斯梯度模（Laplacian Sum，LS）和灰度平均梯度（Gray Mean Grads，GMG）［13］来衡量图像的复原效果。

各算法复原结果如下所示。

实验1：Levin数据集模糊图像测试。

从图3可以看出，文献［1］IBD算法复原结果最差，不仅没有恢复出图像纹理细节，复原结果还有重影现象。文献［12］和文献［7］复原结果略有改善，但是复原图像存在较大的边缘振铃效应，比如小孩的鼻梁处、左眼眼眶处仍然存在一些伪迹，而本文算法恢复出了较多的图像细节，图像整体比较平滑，这是因为本文算法利用提取的强边缘回复图像，避免了弱边缘错误指导图像恢复。另外，从表2各算法复原结果可以看出，本文算法在PSNR、GMG和LS指标上也均优于其他算法。

图3 实验1各算法实验结果对比

表2 实验1各算法指标对比

实验2：现实场景下模糊图像测试。

由图4可以看出，文献［1］未能正确恢复出复原结果。文献［12］的复原图像有较大的波纹，比如图像中人的脖子下方有明显的波纹。文献［7］的复原结果略有提升，但是相对于本文算法，本文的复原结果图像更平滑，视觉效果更好。另外从表3各项指标上对比，本文算法的GMG和LS也优于对比算法。

图4 实验2各算法实验结果对比

表3 实验2各算法指标对比

综上分析，本文算法在主客观图像质量评价方面均都要优于其他对比算法。

5 结语

论文提出一种基于强边缘和稀疏约束的运动模糊图像盲复原算法，首先提取了输入模糊图像的强边缘，然后在多尺度方案下更精细的估计点扩散函数，通过变量分离交替迭代代价函数，当满足收敛条件时，得到最终的估计图像。通过公开数据集和现实模糊图像的测试，验证了算法的有效性和适用性。