一种基于非线性滤波的重力匹配定位算法∗
岳 灿官 斌
(1.武警湖北省总队 武汉 430070)(2.海装驻武汉地区第七军事代表室 武汉 430223)
1 引言
惯性导航系统以陀螺仪和加速度计为核心敏感器件,可以在保证自主性的前提下获取导航信息,具有数据更新率高、导航信息完整可靠等突出优点[1]。自20世纪70年代起,立足于制造技术和计算机技术的发展成果,惯性导航系统已在军事打击、军事侦察、地质勘探等领域得到大规模应用。同时,随着高性能惯性器件技术和高可靠系统技术的越发成熟,惯性导航系统必将为生命健康、信息技术、能源、材料等前沿科技热点的发展提供重要支撑,具备广阔应用前景[2]。
惯性导航系统需要通过积分运算来实现定位解算,其必定面临定位误差长期累积的限制,不利于水下潜航、远洋导航等对长航时自主定位精度要求较高的领域。针对上述限制,为不破坏系统的自主性,主要包括以下几种解决方案:陈剑从惯性器件本身出发[3],通过研究提高陀螺仪基本性能的技术,直接改进惯性器件性能来提高惯导系统精度,从源头抑制惯导系统误差发散趋势,但其面临性能提升瓶颈、研发周期长等限制;Zhi-Liang Deng将经典控制理论引入惯导系统的姿态更新过程[4],采用系统误差阻尼策略,可以有效改善系统振荡误差特性,实现周期振荡相关误差的有效抑制,但无法解决陀螺漂移引起的累积性位置误差;刘生攀根据惯导系统误差特性[5],将旋转调制技术引入惯性导航系统,通过特殊的调制转位设计可以抵消器件的对称性误差,能够在不提高惯性器件性能的前提下大幅提高整体定位精度,是提升系统精度的有效手段,但无法从根本上解决位置误差漂移问题;YF Chen将实测重力相关信息作为观测量[6],利用重力匹配技术来实现系统误差的修正,从而有效重调系统初始位置,能够从根本上解决定位误差长期累积问题,具有良好的研究价值和应用价值。
综上所述,针对长航时惯性导航系统面临的位置误差发散问题,本文以重力匹配为核心思想,提出一种基于非线性滤波的重力匹配定位算法。该算法基于惯导系统误差模型,将重力信息作为观测量,并结合非线性滤波技术和量测噪声自适应技术,能够实时估计系统的定位误差。半物理仿真结果表明,本文提出的重力匹配定位方法可以实现0.61海里/20天的定位精度(3σ)。
2 重力匹配架构
重力匹配导航是以重力测量为基础发展起来的无源导航,这类导航方式首先需要制备离线重力数据库,然后利用搭载在运载体上的重力敏感仪器实测重力场,再采用有效的匹配算法获取基于实测重力场对应的位置信息,最终修正载体位置误差,如图1所示。可以看出,研制高精度重力测量设备、构建高分辨率重力数据库以及设计有效重力匹配算法是重力匹配导航的三大关键技术[7~9],其中有效重力匹配算法作为实现重力匹配定位的核心,其性能将直接影响总体精度。
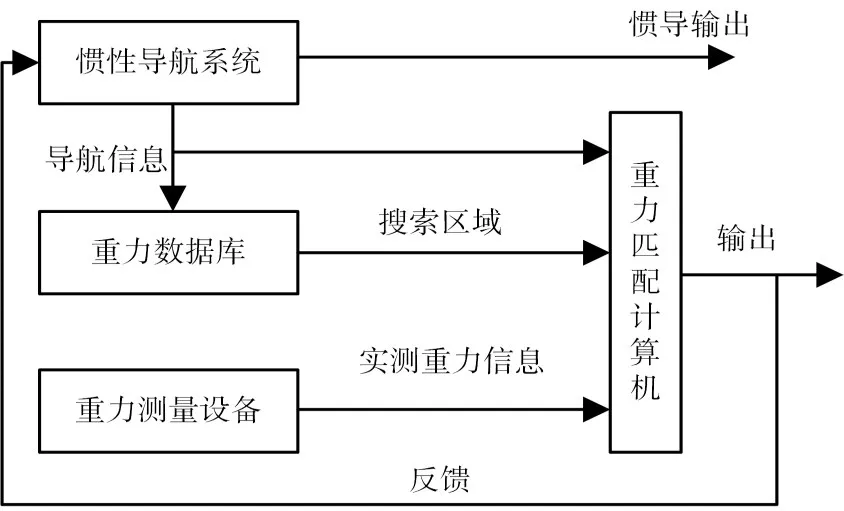
图1 重力匹配流程图
3 一种基于非线性滤波的重力匹配定位算法
3.1 滤波模型构建
3.1.1 系统状态模型
根据惯导系统误差传播特性[10],选取13维状态变量来描述系统特征:

式中,状态变量按先后顺序为经度误差、纬度误差、东向速度误差、北向速度误差、东向姿态误差角、北向姿态误差角、天向姿态误差角、x方向加速度计偏置、y方向加速度计偏置、z方向加速度计偏置、x方向陀螺仪偏置、y方向陀螺仪偏置,z方向陀螺仪偏置。根据上述状态变量,选取状态模型为
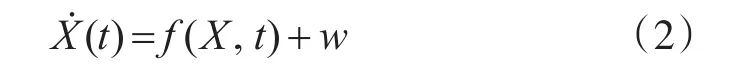
式(2)中,w为取决于器件性能的系统噪声;f(X,t)为状态模型解析式,其具体形式为

3.1.2 非线性观测模型构建
重力匹配过程中,需要利用观测模型来表示实测重力测量值和载体位置误差之间的关系,观测模型通用形式如下:
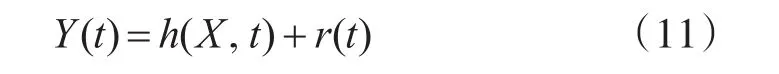
式中,Y(t)为观测量,h(X,t)为观测模型,r(t)为观测噪声。首先令观测量Y(t)的物理含义为
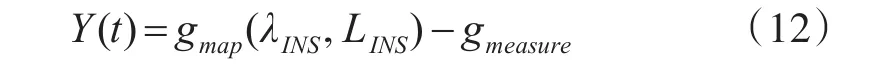
式中,λINS,LINS分别是源自惯导的经度和纬度;gmap(,)表示重力数据库输出函数(本质上是某种插值或拟合方法);gmap(λINS,LINS)表示按照经度为λINS且纬度为LINS,由重力数据库和重力数据库输出函数获取的重力信息;gmeasure是载体上重力测量设备获取的重力信息。所以,为配合Y(t)的物理含义,式(12)中h(X,t)的解析形式为
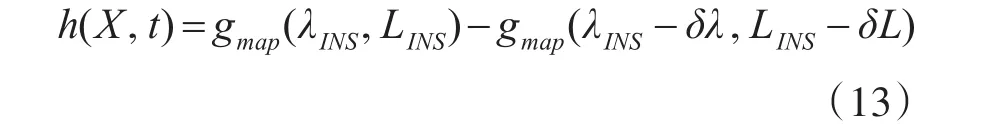
将式(12)、式(13)带入式(11),得到量测方程的最终形式:
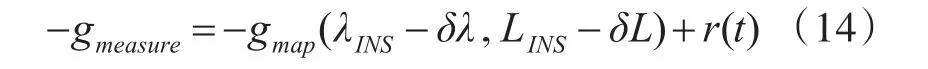
基于式(14)可知,量测方程取决于重力数据库输出函数gmap(λINS-δλ,LINS-δL)和量测噪声r(t)。
3.2 扩展卡尔曼滤波
扩展卡尔曼滤波是卡尔曼滤波的次优估计形式,适用于滤波模型中存在非线性的情况[11]。已知某系统的非线性状态方程和观测方程为
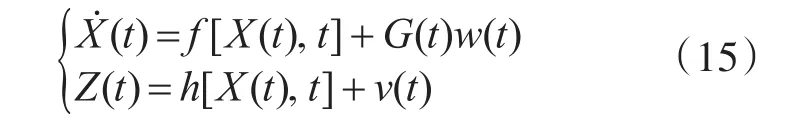
式中,X(t)为系统状态量,Z(t)为观测量,f[X(t),t]为非线性系统模型,h[X(t),t]为系统观测模型,G(t)为噪声驱动矩阵,w(t)为过程噪声,v(t)为观测噪声。根据泰勒展开,对式(15)进行线性化近似,得到状态变化的系统模型:

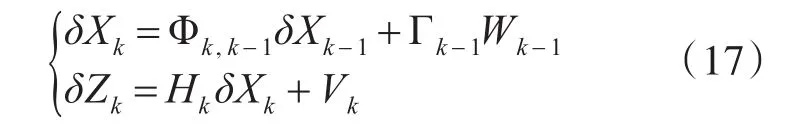
再根据状态变化的离散系统模型,得到状态估计的滤波基本方程:

3.3 重力数据库输出函数构建
由3.1.2节可知,重力数据库输出函数gmap(,)是构造非线性观测模型的核心。有学者[12]将高程信息用多项式曲面拟合,得到了较好的应效果。考虑到重力数据和高程信息具有一定的相关性,本文采用3次多项式曲面来重构重力数据库,从而完成重力数据库输出函数gmap(,)的构建,数据库输出函数模型为
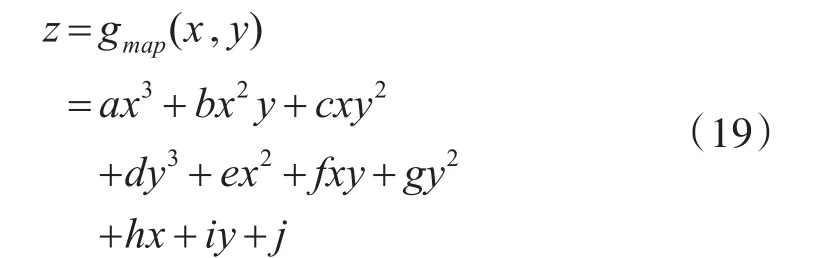
式中,z为重力信息,a,b,c,d,e,f,g,h,i,j为带拟合系数,x为目标位置的经度,y为目标位置的纬度。
4 半物理仿真
4.1 仿真条件设置
4.1.1 惯性数据设置
为验证本文提出算法的有效性,本文采用某惯导设备的动态海测数据进行半物理仿真,数据详细信息如表1所示。仿真过程中,利用海测数据进行初始对准及无阻尼纯惯性导航解算,为重力匹配定位算法提供基本的导航参数,同时,基于卫星导航位置信息,评价算法的匹配定位精度。

表1 仿真数据说明
4.1.2 重力数据设置
重力数据设置包括数据库和实测重力数据生成两方面。本文选用加利福尼亚大学于2014年发布的海洋重力数据库进行仿真,数据库具有1′的分辨率,由CryoSat-2卫星和Jason-1卫星的测高数据以及已有重力数据融合而成,具有相对更高的精度。同时,加利福尼亚大学给出了该数据库详细下载地址,利于实现重力匹配仿真验证。而且,为模拟获取用于重力匹配的实测重力信息,本文采用卫星导航位置信息和3.3节所述的重力数据库输出函数来仿真生成实测重力信息,并在仿真生成的实测重力信息上叠加标准差为1mGal的噪声来模拟真实数据。
4.2 仿真结果
进行数据时长约为20天的半物理仿真,得到匹配算法定位误差和纯惯性定位误差的对比图,如图2和图3所示,且各误差的统计结果如表2所示。

图2 经度误差仿真结果

图3 纬度误差仿真结果

表2 仿真结果统计
由表2可以看出,本文所提出的重力匹配算法具有0.48海里/20天(3σ)的纬度误差和0.38海里/天的经度误差(3σ),优于纯惯导定位,且无明显发散迹象。
5 结语
重力匹配作为一种可以在不破坏惯导自主性条件下重调惯导系统位置的有效手段,已经逐步成为了长航时自主导航的发展热点。为此,本文瞄准重力匹配的应用发展方向,提出了一种基于非线性滤波的重力匹配定位算法,该算法依据重力信息具备的空间相关性,构造系统状态模型和非线性量测方程,并结合扩展卡尔曼滤波技术和三次曲面拟合技术,完成对惯导系统位置误差的有效估计。半物理仿真结果表明,本文提出的重力匹配定位算法可以实现0.61海里/20天(3σ)的定位精度,且无明显发散迹象。

