基于改进Kalman的传感器数据加权处理算法
陈艳春,达钰鹏
(1.石家庄铁道大学,河北 石家庄 050043;2.河北省人力资源和社会保障厅信息中心,河北 石家庄 050071)
0 引 言
任何传感器的测量都是带有误差的,误差产生的原因既有设备本身的问题,在数据采集过程中,如受传感器老化,也有转换器以及无线电传输过程中的干扰,使得接收数据中经常会产生异常跳变点,这种偏离的数据点被称为异常值[1]。异常值分为两类,一种是孤立的虚假异常值,这类异常值一般是孤立出现,属于噪音的一种;另一种是真实的异常值,这类异常值一般连续出现,反映观测对象发生异常变化。
在物联网监测中,为了兼顾计算成本和计算量,常常采用SPC、PCA等方法对建筑等监测对象进行异常识别[2-3]。此类基于统计的方法可以基于历史数据实现对异常的识别,其理论基础是经过实践检验的[4]。但这类算法对输入数据的准确性要求较高,直接使用未经处理的原始数据极易发生误报。同时,因为使用场景的不同,很多传感器的观测误差存在周期性变化,处理算法如果采用静态参数,则无法拟合周期性变化。
为了解决实时监控中由于虚假异常值出现产生的误报问题,常用的手段有两个[5-6]。一是在同一位置部署多个同类型传感器同时采样,利用传感器误差近似正态分布的特点,利用统计学方法中的拉伊达法或格拉布斯法剔除虚假异常点后计算平均值,可以实现对噪音和孤立虚假异常点的较好过滤,当传感器数量较多时使用拉伊达法,较少时使用格拉布斯法。这类基于统计理论的方法的优势是计算方法简便,通用性强,鲁棒性好,在系统边缘节点便可部署使用,天然适合分布式部署,但缺点是需要在单个位置部署大量传感器,系统硬件部署和维护成本较高。二是利用各种滤波手段对单个传感器数据进行实时修正。例如小波分析、Kalman滤波等,但这类滤波手段也存在着一些不足。以Kalman滤波算法为例,Kalman滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法,本质是利用两个正态分布的融合仍是正态分布这一特性迭代最优估计值。Kalman滤波虽然性能优越且得到大量实践证明其正确性,存在的不足是:由于无法确定测量过程中的系统噪声和量测噪声特性,只是试验中给定了Q和R的噪声参数,而Kalman滤波是基于精确数学模型递推的过程。随着测量时刻的不断增加,根据递推公式求得的P(k|k)会逐渐趋于0或者某一稳态的常数,但是最优观测值X(k|k)与实际数据的差距越来越大,这种情况下,Kalman滤波器的预测和估计的功能逐渐丧失。而且由于滤波的实现平台在计算式计算误差的不断累计传递也可能会使滤波器出现发散的现象[7]。同时,这类滤波算法参数调试复杂,而随着传感器设备老化,设备误差会变化,相应参数也需要做出调整,需要长期跟踪滤波效果,适时调整算法参数,增加了日常维护人员的工作负担[8]。
基于以上,该文提出一种结合以上两种手段的传感器实时数据处理算法,通过高频率采样,将单传感器单位时间内多次采样值看作为多传感器的一次采样值,用统计方法剔除虚假异常值后的观测值,再利用Kalman滤波处理求得最优估计值,较好地解决了虚假异常值产生的误报问题。
1 算法描述
该文提出的算法,根据实践中观测值短期内存在变化自相关性,而长期内正态分布的特点[9],将单位时间段内传感器监测数据看作一个线性定常系统。假设在单位时间段内所观测的值是恒定的,可将单传感器多次采样值看作为多传感器的一次采样值,则该时间段内传感器的观测误差和噪音都是近似正态分布的,那么基于该值计算的移动平均值也是近似正态分布的,这样的情况下是可以通过Kalman进行数据融合的。
首先,利用统计方法剔除虚假异常值影响,再用移动平均值降低随机噪音的影响。滑动窗口方式获取数据,设采样传感器数为N,当N>100时,采用拉伊达法即3西格玛法,计算观测值Xi与平均值X残差的绝对值Vi,当Vi大于3倍标准差std即(|Xi-X|≥3*std)时,认为该观测值为异常值,剔除所有异常值后计算剩余值的平均值gbmean。当N≤100时,采用格拉布斯法,根据n和显著性水平a计算g(n,a),将观测值从小到大排序,计算最大值和最小值各自与平均值的残差的绝对值Vi,当Vi>g(n,a)*std,判断其为异常值剔除,并重新计算剩余观测值的均值和std,重复以上步骤直至没有出现异常值,而后计算剩余值的平均值gbmean[10-11]。格拉布斯法相较于拉伊达法更严谨准确,但由于需要排序和反复计算均值、标准差,当N较大时计算量较大,而当N>100时候,其结果和拉伊达法接近,为简化计算可使用拉伊达法剔除异常值[12]。
然后,利用Kalman滤波计算最优估计值。以gbmean作为经验值,移动平均值f作为观测值,二值单位时间内各自标准差作为其观测误差,而后根据上一次滤波时f值和gbmean值各自与t值的绝对误差进行加权融合出新的误差std1和std2,这样的误差结合传感器自身最近误差以及与最优估计值误差,当出现孤立异常值时更相信gbmean值,当出现连续异常值时更相信f值。
实时计算Kalman增益,根据一元卡尔曼滤波增益系数计算公式(1):
(1)
计算出最优估计值t。文中f值和gbmean值的误差并非如在经典Kalman滤波中是估计值,而是基于单位时间段值滑动数据计算而来的,避免估计中错误累积导致的离散问题。在计算出估计值后,结合历史t值,基于SPC法,根据该时间段t值的采样次数,利用格拉布斯法查表或拉伊达法确定控制限,进行异常值判断。
之所以选择f值和gbmean值进行融合,一是为了解决缺失值问题,由于各种因素,传感器数据出现缺失值是十分常见的,移动均值可以比较好地解决常见线性系统的缺失值填充问题。二是为了更好地识别连续出现的异常值。如果直接使用带有噪音的原始观测值,f值虽然可以改善但仍无法完全剔除虚假异常值影响,很容易出现误报;而仅使用gbmean值,由于会将第一个出现的真实异常值认为是虚假异常值,需连续出现的异常值影响总体方差后才能体现异常情况,故对于真实发生的异常反应具有滞后性。该文使用了Kalman法将f值和gbmean值进行融合,当异常值连续出现时能够较快反映异常情况,在解决孤立虚假异常值的基础上,实现对异常情况的较快反应。
2 算法流程
以图1为例,说明此算法的计算流程。
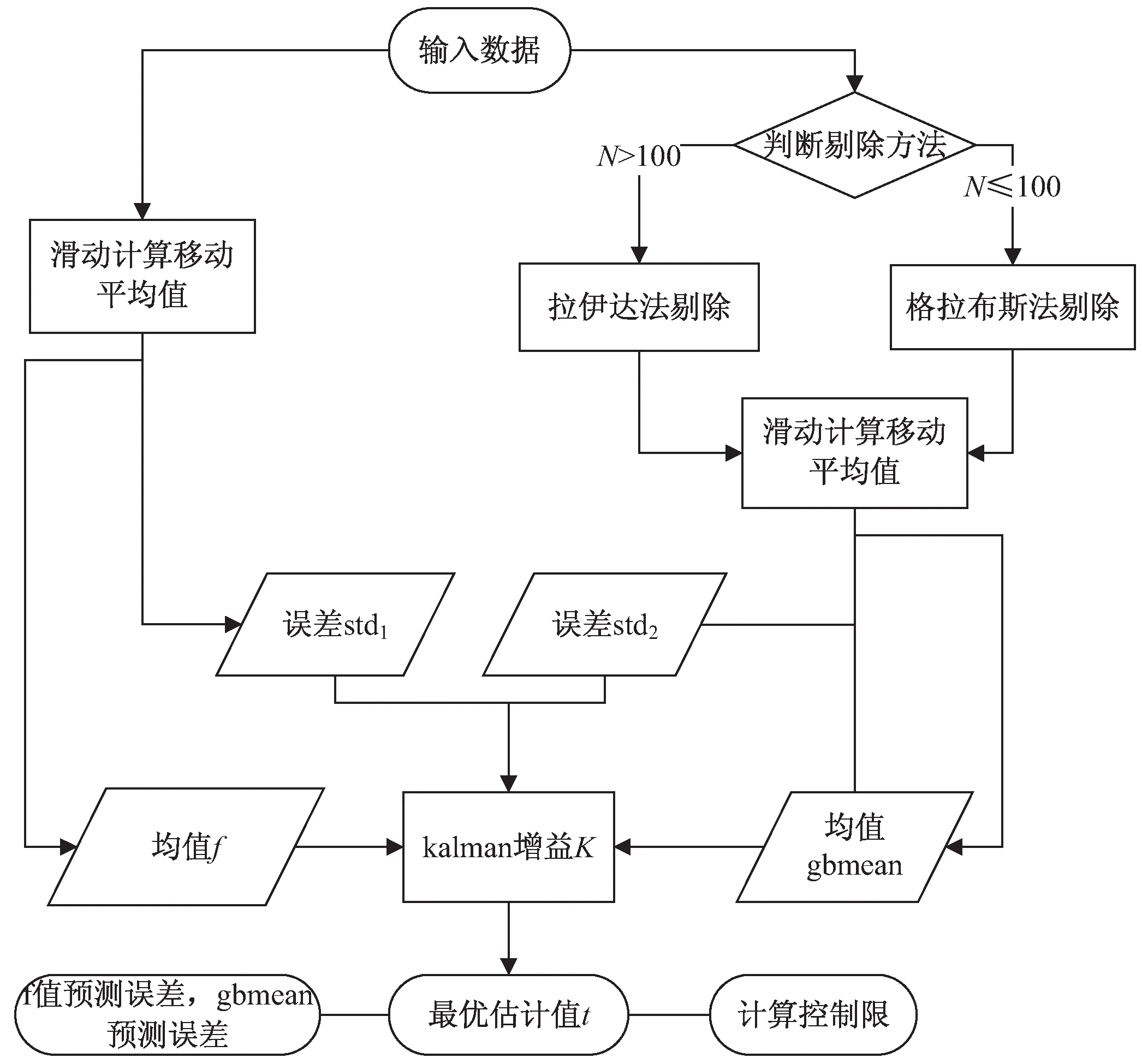
图1 算法流程
第一步:获取Z时间内的所有采样值,先计算Z时间内采样数据的移动平均值f,以其标准差为其观测误差x1,上一次预测绝对误差为x2。根据式(2)~式(4)[13]:
(2)

(3)
std1=w1*x1+w2*x2
(4)
计算其误差std1。而后,如采样次数N≤100时,根据设定的显著性水平a,利用格拉布斯法剔除异常值后计算移动平均值gbmean;当N>100时,利用拉伊达法剔除异常值后计算移动平均值gbmean,以其标准差为其观测误差x3,上一次预测绝对误差为x4,计算其误差std2。
第二步:移动窗口取数据进行滚动计算,实时更新f值和gbmean值及其各自误差,根据式(1)计算K值,进而根据Kalman校正式(5):
t=gbmean+K*(f-gbmean)
(5)
求出最优观测值t,并计算Z时间段内各采样点t值的标准差std3。
第三步:计算控制限,当N>100时,Vi控制限为3*std3;当N≤100时,需根据格拉布斯法则计算g(n,a),Vi控制限为g(n,a)*std3。超出控制限的为异常值。
整个算法中需要设定的参数只有N以及使用格拉布斯法时的显著性水平a,也只需存在N个f值、N个gbmean值和N个t值共3N个值,所需存储量和计算量较小,调整参数难度较低,可在物联网终端或边缘服务器进行数据处理,实现分布式部署。
3 仿真数据验证
3.1 数据准备
该文所采用的数据源于石家庄站铁路站房2013年7月至2014年7月数据中的M16BL-1传感器数据data2,在anaconda3环境下进行数据分析。为了验证算法的滤波性能,在已有数据基础上,将采样密度调整至每分钟一次,结合原始值利用pandas中线性插值法填充调整后产生的缺失值,生成数据525 583条,填充后数据折线趋势图如图2所示。

图2 data2趋势图
而后先利用numpy.randon.normal函数生成均值为0,标准差为8的正态分布随机噪声,再利用numpy.randon.randint函数生成1 000个[50,100]和1 000个[-100,-50]的随机异常值点,这些异常值随机分布,有孤立有连续,data2值加上噪音和异常值点的数据为etl2值,也就是要处理的数据值,折线趋势图如图3所示。
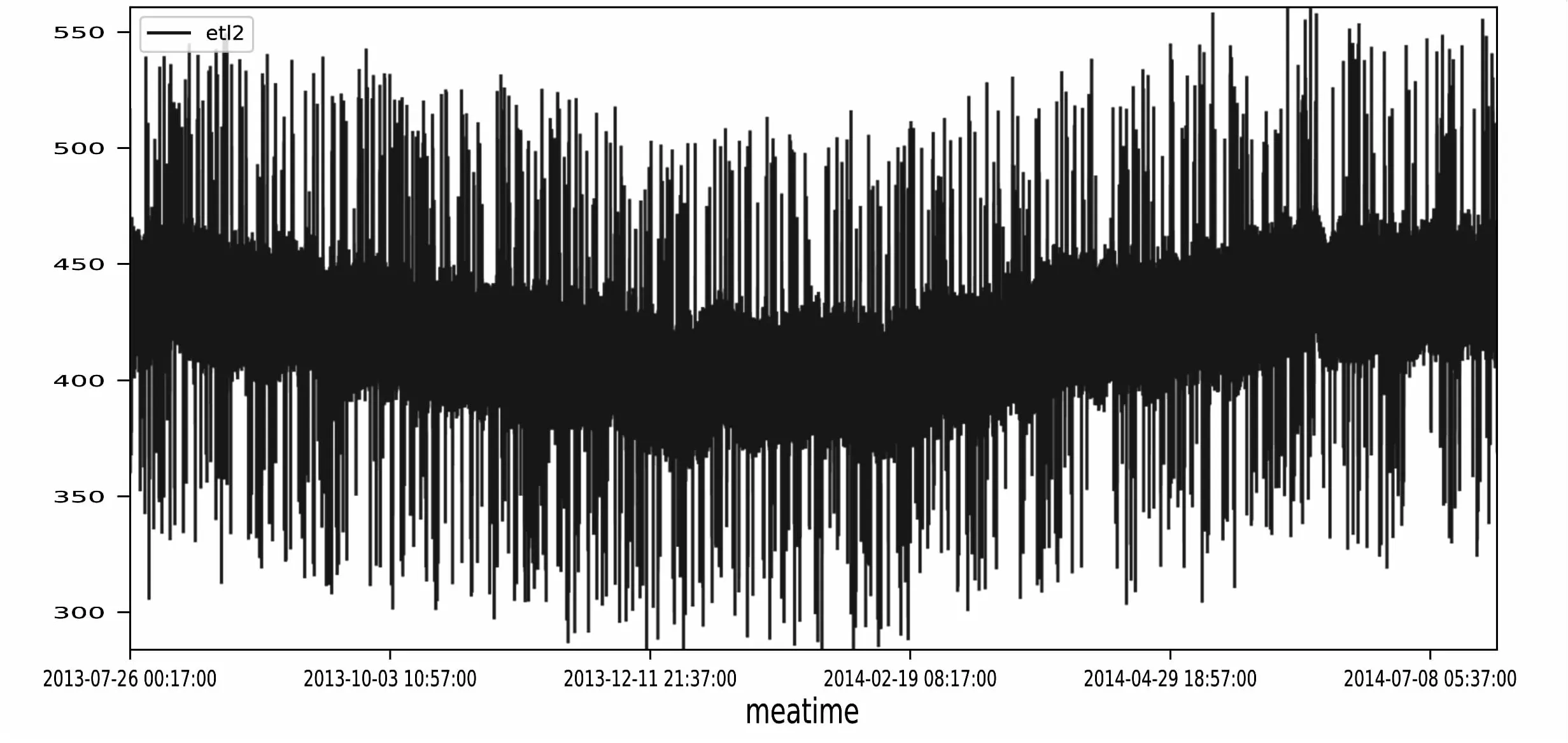
图3 etl2趋势图
数据表格式如表1所示。

表1 处理前数据
当然,为了更加直观地体现算法处理效果,增加的噪音和异常值较为明显,实际异常值不会这么多。
3.2 算法实现
在算法实现上,为了快速实现,采用python语言进行开发,在anaconda3环境下,使用了pandas、outliters、math包。其中格拉布斯法是outliters包的smirnov_grubbs函数实现。移动平均值使用pandas.dataframe.rolling函数计算,由于采用数据的短期内自相关而长期内正态分布的特点,根据参考文献[10]的统计结果,选取15分钟作为Z时间段长短,设置滑动时间窗口为最近15分钟的采样数据,移动平均值为f15,即N值为15,数据以dataframe格式存储为df1,显著性水平为0.99,初始预测误差为15,gbmean值和t值计算代码如下:
Import pandas aspd
Import matplotlib.pyplot as plt
From sklean.metrics import mean_squared_error
From sklean.metrics import mean_absolute_error
Import numpy as np
Form outliers import smirnov_grubbs as grubbs
Import math
df1=pd.read_csv("含噪音数据.csv")
df1['gbmean']=None
df1['t']=None
df1['vi1']=None
df1.loc[14,'vi1']=15
df1.loc[14,'vi2']=15
for i in range(15,len(df1)):
s=grubbs.test(df1.loc[i-14:i,'etl2'],0.99)
df1.loc[i,'gbmean']=s.mean()
std1=df1.loc[i-14:i,'f15'].std()
x1=df1.loc[i-1,'vi1']
x2=df1.loc[i-1,'vi2']
w1=cou(std1,x1)
w2=1-w1
std2=s.std()
w3=cou(std2,x2)
w4=1-w3
std1=std1*w1+w2*x1
std2=std2*w3+w4*x2
stdx2=math.pow(std2,2)/(math.pow(std2,2)+math.pow(std1,2))
f1.loc[i,'t']=df1.loc[i,'gbmean']+stdx2*(df1.loc[i,'f15']-df1.loc[i,'gbmean'])
df1.loc[i,'vi2']=abs(df1.loc[i,'t']-df1.loc[i,'gbmean'])
df1.loc[i,'vi1']=abs(df1.loc[i,'t']-df1.loc[i,'f15'])
计算出gbmean值、t值后,去除少量由于移动均值计算产生的缺失值,数据如表2所示。

表2 处理后数据

续表2
利用matplotlib包进行数据可视化,趋势图如图4和图5所示。

图4 gbmean趋势图

图5 t趋势图
计算出t值,每次计算最近15个t值的均值xt和方差stdt,当N=15,显著性水平为0.99时,最优估计值的残差g(n,a)=g(15,9)=3.292,当|t-xt|>3.292*stdt时,判断发生异常。
3.3 结果验证
首先,利用matplotlib包进行数据可视化,比较将f15、gbmean、t和真值data2值放在一张图里进行对比,定性比较处理效果,由于数据集较大,图6是整体滤波效果。

图6 滤波效果图
然后用sklean.metrics包进行定量比较。计算etl2、gbmean、t与data2值的均方误差(MSE)和平均绝对误差(MAE),MSE是最常用的回归损失函数,计算方法是求预测值与真实值之间距离的平方和,MAE是目标值和预测值之差的绝对值之和的平均值。MSE会赋予异常点更大的权重,也就是说对预测误差给予更大的权重,用MSE可以比较方法对异常值处理的好坏,而MAE值体现了误差,显示了方法处理的性能。源数据etl2的MSE约为119.45,f15值的MSE约为7.99,gbmean值的MSE约为8.00,t值的MSE约为6.98,t值的MSE相较于gbmean下降了12.73%;处理前数据etl2的MAE约为7.04,f15值的MAE约为2.11,gbmean值的MAE约为2.23,t值的MAE约为2.03,t值的MAE相较于gbmean下降了8.72%。
同时计算各采样点f15值、t值和gbmean值相较于真值data2绝对残差的标准差,f15值残差标准差约为1.88,t值残差标准差约为1.68,gbmean值残差标准差约为1.74,t值残差标准差相较于gbmean值残差标准差降低了3.18%,算法效果较为稳定。综上可知,该算法性能和可靠性提升明显。
3.4 对预测效果提升的验证
为了进一步证明数据处理对预测结果的影响,该文以工业界常用的lightgbm算法为例,对处理前后的数据进行模型训练和预测。LigthGBM是决策树预测模型(GBDT)的一种,由微软提供,它和XGBoost一样是对GBDT的高效实现,原理上它和GBDT及XGBoost类似,都采用损失函数的负梯度作为当前决策树的残差近似值,去拟合新的决策树。基于Histogram的决策树算法,更低的内存占用和更快的处理速度,基于OpenMP多线程加速和基于OpenCL的异构加速,可以利用多种硬件加速学习过程,应用范围更广[14]。
首先,利用上文的处理算法对数据进行处理;然后,对于周期性较强的时间序列问题,可以通过将时间序列问题转化为回归问题进行预测,这里将时间这一特征进行特征工程处理,分解出表3的10个特征。

表3 训练特征
然后,分别使用原始数据etl2和处理后数据xmean1进行lightgbm模型训练,这里由于已经是回归问题,故采用随机抽取的方式取75%的数据为训练集,25%的数据为测试集,以MSE值作为训练依据,以ETL2值训练的模型MSE值为118.447,以xmean1值训练的模型MSE值为7.762 15,数据处理后模型预测的MSE值下降了93.44%,性能提升明显。
4 结束语
该算法结合了现有物联网数据处理中的两种处理方法,将多传感器数据测量方法应用于单传感器数据处理,兼顾了成本和准确性,可以解决实际工作中物联网大量传感器高采样次数,传感器误差存在周期性变化的场景,实现动态剔除异常值、实时滤波和实时计算控制限。相较于传统Kalman滤波法,调整参数少,维护成本低;相较于神经网络等机器学习方法,计算量和存储数据量小,适合实时数据处理和分布式进行部署。

