离散数学中命题逻辑的应用研究
杨井荣,李思莉
(成都理工大学 工程技术学院 计算机科学系,四川 乐山 614007)
0 引 言
计算机算法的实现不仅依靠硬件,还必须依靠那些能够让硬件运行下来的各种编制的程序软件。计算机硬件是由很多逻辑电路所组成的,而逻辑电路是建立在布尔代数的命题逻辑的基础上的,命题逻辑运算就可以变成布尔代数的演算[1]。可见,计算机硬件与逻辑之间的这种关联直接导致计算机软件与逻辑之间存在密不可分的联系。编程的过程也是算法形成的过程,算法是在计算机功能的基础上完成的[2]。现实中,计算机的操作是在基本的逻辑运算基础上生成算法,并最终用这些基本的运算元来代替的计算完成的[3]。
命题逻辑是现代逻辑较简单、较基本的组成部分,它不考虑把命题分析成个体词、谓词和量词等非命题成分的组合,只研究由命题和命题联结词构成的复合命题,特别是研究命题联结词的逻辑性质和推理规律[4]。命题逻辑分为经典命题逻辑和非经典命题逻辑,后者如构造逻辑、模态逻辑等逻辑系统中的命题逻辑部分[4]。历史上最早研究命题逻辑的是古希腊斯多阿学派的哲学家,现代对命题逻辑的研究始于19世纪中叶的G.布尔,G.弗雷格则于1879年建立了第一个经典命题逻辑的演算系统[5]。命题逻辑是研究关于命题如何通过一些逻辑连接词构成更复杂的合理以及逻辑推理的方法[6]。
1 命题逻辑在计算机语言中的运用
逻辑推理和判断方面的问题,用常规的方法很难或者根本无法求解出来,这个时候就理所当然地想到使用计算机编程求解。使用语言编程不一定就能够轻易地解决问题,还涉及到解决问题的算法设计问题。因此算法的设计就是解决各种问题的核心和关键。通过详述若干有关逻辑推理和判断问题的推理过程有助于设计出更高效的算法[7-8]。
1.1 推理问题
例:一个宿舍里有A、B、C、D、E五人,现在调查这些人的毕业去向问题。
(1)A与B中必有一个人出国;
(2)若A出国,则C不出国;
(3)若D出国,则E也出;
(4)若D不出国,则C出国;
(5)E不出国。
解:对简单命题进行形式化。A:A出国;B:B出国;C:C出国;D:D出国;E:E出国。
形式化前提:A∨B,A→┐C,D→E,┐D→C,┐E
求解过程如下:
(1)┐E 前提引入
(2)D→E 前提引入
(3)┐D (1)(2)拒取式
(4)┐D→C 前提引入
(5)C (3)(4)假言推理
(6)A→┐C 前提引入
(7)┐A (5)(6)拒取式
(8)A∨B 前提引入
(9)B (7)(8)析取三段论
也就是说,B出国。
1.2 如何分工
例:在一所高中,学校每天安排四个人分别打扫学校操场,教学楼,办公楼以及食堂这四个地方的卫生。在某个周一,轮到了甲,乙,丙,丁四个人打扫卫生。但是,学校监督人员在进行例行卫生检查时发现这四个地方的卫生都不合格,所以学校要调查清楚他们之间的分工情况。当学校在向学生调查他们彼此间的分工时,得到了如下的事实:
(1)我在给老师送作业时,看到打扫办公楼的不是同学丙也不是同学甲;
(2)打扫教学楼的肯定是甲和丙中的一个;
(3)如果丁在打扫食堂,那么在办公楼里打扫的那个人应该是甲;
(4)我在食堂吃早饭时,看到打扫食堂的是丁和乙中的一个;
(5)如果乙在打扫食堂,我可以确定打扫教学楼的就是我朋友甲了。
请根据以上事实,确定甲乙丙丁四人分别应负责哪个地方卫生?
解:对简单命题进行形式化。
p:甲打扫办公楼;q:丙打扫办公楼;
r:甲打扫教学楼;s:丙打扫教学楼;
t:丁打扫食堂;u:乙打扫食堂。
m:乙打扫办公楼;n:丁打扫办公楼
形式化前提:┐p∧┐q,(r∧┐s)∨(┐r∧s),t→p,t∨u,u→r,p∨q∨m∨n,p→┐q,r→┐s,t→┐u,p→┐r,q→┐s,u→┐m 。
求解过程如下:
(1)t→p 前提引入
(2)u→r 前提引入
(3)t∨u 前提引入
(4)p∨r (1)(2)构造性二难
(5)┐p∧┐q 前提引入
(6)┐p (5)化简
(7)┐q (5)化简
(8)r (4)(6)析取三段论
(9)r→┐s 前提引入
(10)┐s (8)(9)析取三段论
(11)t→p 前提引入
(12)┐t (6)(11)拒取式
(13)t∨u 前提引入
(14)u (12)(13)析取三段论
(15)u→┐m 前提引入
(16)┐m (14)(15)假言推理
(17)p∨q∨m∨n 前提引入
(18)n (17)(5)(8)(16)析取三段论
(19)r∧u∧n (8)(14)(18)合取引入所以,甲打扫教学楼(r),乙打扫食堂(u),丁打扫办公楼(n),丙打扫操场。
其实,这类问题通过表格的形式(见表1),用穷举法可以非常快速地求解[9]。

表1 穷举法求解分工问题
由表1知:甲打扫教学楼;乙打扫食堂;丙打扫操场;丁打扫办公楼。
1.3 逻辑学家的推理
例:有一逻辑数学家误入某个部落,他被拘于牢,酋长意欲放行,他对逻辑学家说:“今有两门(A、B),一为生门,一为死门,你可以开启任意一门。为协助你离开,今加派两名战士(甲、乙),负责回答你提出的任何问题。惟可虑者,此两战士中一名天性诚实,一名说谎成性,今后生死由你自己选择。”[10]
逻辑学家沉思片刻,走到A门前,问战士甲:“战士乙将判断A门为死门,对吗”?战士甲回答“对”。逻辑学家开A门从容而去。
试用真值表及范式说明理由。
解:简单命题形式化。
p:战士乙(不妨假设为诚实人)判断A门是死门
q:战士甲(不妨假设为说谎人)对战士甲的判断(q=┐p)
r:A门是生门(r=┐p)
根据题意可得真值如表2所示。

表2 生死门真值表
即战士甲的回答是“是”时,A门是生门,逻辑学家可从A门离去;
当战士甲的回答是“否”时,A门是死门,逻辑学家从B门离去。
1.4 程序下载
例:设有一个在Internet上下载新闻的程序[11],为避免程序产生死循环和重复下载同一个新闻条目,程序必须根据下述4个条件对给定的一个新闻条目判断是否执行下载任务:
条件一:该新闻条目在程序的前一次执行中已下载,用命题符号E表示;
条件二:该新闻条目在程序的本次执行中已下载,用命题符号N表示;
条件三:该新闻条目是一个动态更新的新闻条目,用命题符号D表示;
条件四:该新闻条目已过期,程序需要重新下载,用命题符号Q表示。
执行下载任务的规划是:
(1)该新闻条目在程序的前一次执行中未下载,则不论其其他条件如何,一定执行下载。┐E→A
(2)如果是一条动态新闻,并且该新闻条目在程序的本次执行中没有下载,则执行下载,否则不执行下载;D∧┐N→A
(3)如果新闻条目在程序的前一次执行中已下载,并且该新闻条目在程序的本次执行中没有下载,那么:如果是一个过期的新闻条目,则执行下载,否则不执行下载。
通过命题逻辑中所学的知识,设计一个真值表,判断程序是否应该执行程序[12]。
解:其对应的真值表如表3所示。

表3 程序下载真值表
1.5 人员录取方案
例:某公司要从3名应聘人A、B、C中录取1~2名进行签约。根据面试情况,录取时要满足以下条件:
(1)若录取A,则也录取C。
(2)若录取B,则不录取C。
(3)若不录取C,则同时录取A与B。
请用命题逻辑推断可能的录取方案[13]。
解:对简单命题进行形式化。A:录取A;B:录取B;C:录取C。
则形式化前提:A→C,B→┐C,┐C→A∧B。
则G=(A→C)∧(B→┐C)∧(┐C→A∧B),则G的真值表如表4所示。

表4 人员录取真值表
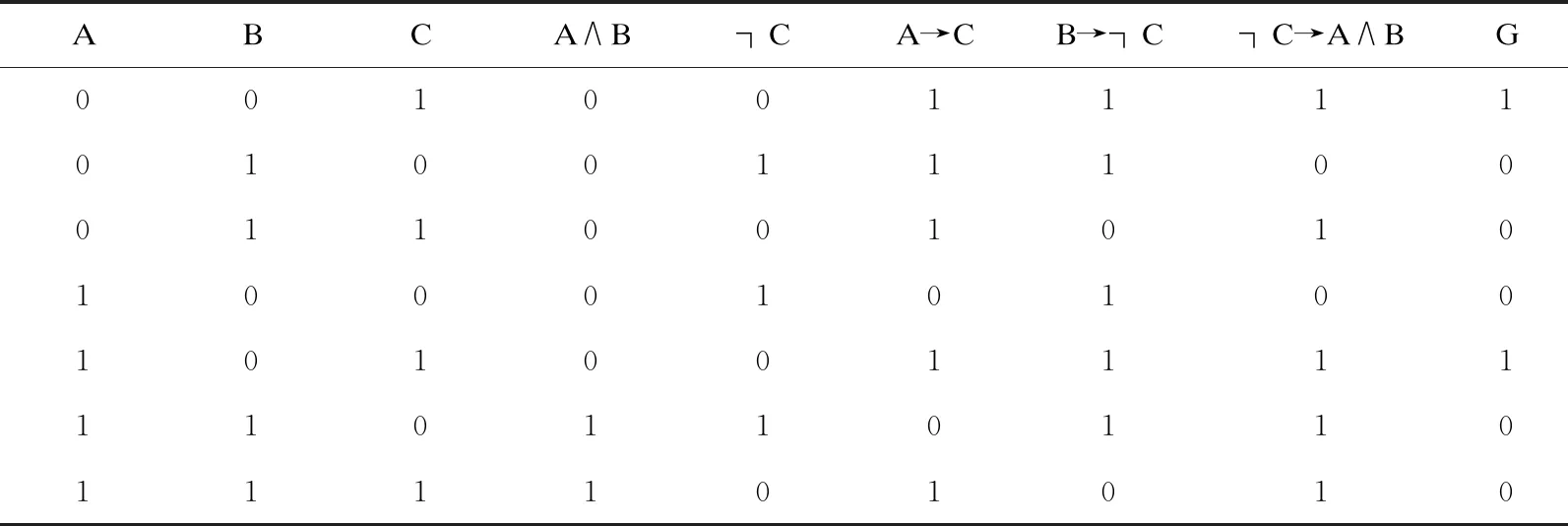
续表4
从真值表可以看出,有两种录取方式:A不录取,B不录取,C录取;A录取,B不录取,C录取。
1.6 排队论的应用
例:设A、B、C、D共4个人进行百米竞赛,观众甲、乙、丙对比赛的结果进行预测[14]。甲:C第一,B第二;乙:C第二,D第三;丙:A第二,D第四。比赛结束后发现甲、乙、丙每个人的预测结果都各对一半。试问实际名次如何(假设无并列者)?
解:设Ai表示A第i名,Bi表示B第i名,Ci表示C第i名,Di表示D第i名,i=1,2,3,4。
则根据题意,有:
(C1∧┐B2)∨(┐C1∧B2)⟺1
(1)
(C2∧┐D3)∨(┐C2∧D3)⟺1
(2)
(A2∧┐D4)∨(┐A2∧D4)⟺1
(3)
因为真命题的合取仍为真命题,所以:
(1)∧(2)
⟺((C1∧┐B2)∨(┐C1∧B2))∧((C2∧┐D3)∨(┐C2∧D3))
⟺((C1∧┐B2)∧(C2∧┐D3))∨((C1∧┐B2)∧(┐C2∧D3))∨((┐C1∧B2)∧(C2∧┐D3))∨((┐C1∧B2)∧(┐C2∧D3))
⟺(C1∧┐B2∧C2∧┐D3)∨(C1∧┐B2∧┐C2∧D3)∨(┐C1∧B2∧C2∧┐D3)∨(┐C1∧B2∧┐C2∧D3)
由于C1和C2不可能同时成立,因此(C1∧┐B2∧C2∧┐D3)⟺0
由于B2和C2不可能同时成立,由于(┐C1∧B2∧C2∧┐D3)⟺0,所以(1)∧(2)⟺(C1∧┐B2∧┐C2∧D3)∨(┐C1∧B2∧┐C2∧D3)⟺1
(4)
(3)∧(4)
⟺((A2∧┐D4)∨(┐A2∧D4))∧((C1∧┐B2∧┐C2∧D3)∨(┐C1∧B2∧┐C2∧D3))
⟺(A2∧┐D4∧C1∧┐B2∧┐C2∧D3)∨(A2∧┐D4∧┐C1∧B2∧┐C2∧D3)∨(┐A2∧D4∧C1∧┐B2∧┐C2∧D3)∨(┐A2∧D4∧┐C1∧B2∧┐C2∧D3)
由于A2和B2不可能同时成立,因此(A2∧┐D4∧┐C1∧B2∧┐C2∧D3)⟺0
由于D3和D4不可能同时成立,因(┐A2∧D4∧C1∧┐B2∧┐C2∧D3)⟺0
由于D3和D4不可能同时成立,因(┐A2∧D4∧┐C1∧B2∧┐C2∧D3)⟺0
所以(3)∧(4)⟺(A2∧┐D4∧C1∧┐B2∧┐C2∧D3)⟺1
综上,知:A第二,B第四,C第一,D第三。
2 命题逻辑在计算机电路设计中的应用
密码锁问题。
例:为了安全,很多民宅或商铺门上都会安装带有报警器的密码锁。现有一种密码锁,工作原理如下:锁的控制电路中有三个按钮A,B,C和—个报警装置。当三个按钮同时按下,或只有A,B两钮按下,或只有A,B中之一按下时,锁被打开;当不符合上述开锁信号时,电铃发响报警。请设计出合理的方案来达到这种效果[15]。
解:用真值表法(见表5)来解决这个问题。令开锁信号G=(A∧B∧C)∨(A∧B)∨(A∨B)。

表5 密码锁问题真值表
据表5,得:
开锁信号G=Π(0,1)=(A∨B∨C)∧(A∨B∨┐C);
报警信号F=(┐A∧┐B∧┐C)∨(┐A∧┐B∧C)。
3 结束语
命题逻辑在计算机和人工智能领域有广泛的应用[16]。该文主要通过推理问题、分工问题、程序下载问题、排队论问题、人员录取问题和密码锁问题论述命题逻辑的应用[17-19]。
总之,在计算机科学的应用中不论是硬件设计还是软件设计都离不开逻辑学的应用[20],逻辑学在计算机科学和人工智能领域都占有基础性地位[21]。现代逻辑学与计算机科学与技术相互融合将进一步推动计算机技术的发展[22]。

