有序Lasso-Logistic模型的电竞角色选择应用分析

王白云，沈春根

(上海理工大学 理学院，上海 200093)

0 引 言

随着社会的进步，如今的电竞早已不再是传统意义上的电子游戏，它正朝着专业体育方向发展，成为一种产业，推动着科技的进步，在现代社会创造了巨大的价值。电竞与其他竞技体育项目一样，对数据的分析和应用有着极高的要求，而机器学习作为现在数据处理和分析的一项主要技术在众多学科领域发挥了不可估量的作用，其中也包括电竞行业。目前国内的电竞行业正处在迅速发展阶段，作为全球电竞行业发展最快、最受关注的国家之一，中国对电竞行业的机器学习研究和分析较为匮乏，使得电子竞技在发展过程中缺少当今最有力的数据参考。通过有序Lasso-Logistic模型分析电子竞技角色选择，为机器学习在电竞分析上提供新的分析方法，使得电竞行业从数据分析上获得更多进展。

该文以著名的电竞游戏─刀塔2为例，采用有序Lasso-Logistic模型分析电竞角色选择，为其他电子竞技角色选择提供参考依据，促进职业选手在角色选择上的策略分析，推动电竞行业向数据化发展。刀塔2主要操作方式是敌对双方(各有五名玩家)之间的对抗，每名玩家从100多个英雄中选择一个进行操作，每个英雄在该局比赛中只能被选择一次。刀塔2包含十余种游戏模式，三种游戏种类。

有序Lasso-Logistic模型包含了自变量对因变量发生具有不同重要性的先验信息，将其用于分析刀塔2以各个英雄为自变量，因变量是比赛结果的数据，探索不同角色选择对比赛的获胜结果的影响，并进行预测，通过与其他机器学习模型的预测结果进行比较突出有序Lasso-Logistic模型良好的预测效果，展现数据自变量先验信息的重要性以及有序Lasso-Logistic模型在分类数据分析中的优越性。

1 文献综述

机器学习中也不乏分类模型，如逻辑回归模型[1-2]、Lasso-Logistic模型[3]、支持向量机模型[4]、随机森林模型[5]以及梯度增强决策树模型[6]等在分类问题中表现出一定的分析能力和预测效果。在分析刀塔2的文章中可看到，许多作者通过玩家所选取的英雄采用不同的分类模型预测游戏结果，如：Semenov、Romov和Korolev等[7]将刀塔2采用了分解机模型分析所选取的英雄并预测刀塔2比赛胜负，通过与其他分类器模型的预测结果相比较显示出分解机模型良好的预测效果。Aznin、Diah和Abdullah[8]构建一个基于规则的技术专家系统向刀塔2玩家推荐适合的英雄，但在系统测试上，作者采取用户问卷调查的评估反馈测试系统的可用性价值，存在较多的不确定因素。Wang和Shang[9]用改进的朴素贝叶斯分类器分析刀塔2玩家选取的阵容预测游戏结果，将预测结果与原朴素贝叶斯分类器的预测结果相比较发现准确率比原朴素贝叶斯分类器至多高1%，虽然预测准确率有所提高，但是并不明显，同样还有文献[10]。另外，一些文献从玩家的角度分析刀塔2，如文献[11-12]。许晨波[13]则提出了改进的LSTM阵容推荐模型和胜率预测模型并设计了相应的系统帮助玩家完善阵容构建，提高获胜几率。陈婷如[14]基于普罗普的功能和LeviStrauss二元对立理论，文本分析了刀塔2与玩家所建立的联系。柯嘉鑫[15]根据K-means算法从刀塔2数据分析了电竞选手。在众多分类模型中发现，少有模型包含自变量的先验信息，比如有序Lasso-Logistic模型中自变量对因变量发生的重要性具有排序的先验信息。在电子竞技中不同角色能力强弱不一，这个信息在选手进行角色选择前便可得知并且对于队伍阵容构建和获胜起到十分关键的作用，对于刀塔2同样如此，但这在上述文章中少有用到。 基于这些原因，该文利用刀塔2中不同英雄选择对比赛的获胜结果存在差异的先验信息，通过有序Lasso-Logistic模型对电竞角色选择进行分析。

有序Lasso-Logistic模型是一含有序约束条件的模型，模型中通过对自变量系数绝对值进行排序形成有序约束条件。这鉴于考虑到在进行数据收集时，选取的自变量对因变量的重要性大小很多时候会存在一些先验性判断，比如该文所采用的刀塔2数据中的自变量cluster ID、游戏模式和游戏类型在进行一局完整的游戏战斗是必不可少的，但就某个英雄而言则非必须，是可选可不选的，重要性较前三者有所降低。有序性约束条件是根据自变量对因变量的重要性大小排序形成，它们可以是根据专业知识或者经验判断，也可以通过变量间的相关性或者重要性计算而得知。有序Lasso-Logistic模型可用于解决自变量对因变量发生存在不同重要性且因变量是二分类的问题，模型结合了变量系数有序约束条件，对多变量分类数据进行分析，使得众多自变量对因变量发生的重要性大小体现得更加明显，使其具体化、显现化。

该文通过分析刀塔2英雄选择作为具体例子，旨在表明有序Lasso-Logistic模型对电竞角色选择的分析效果，体现机器学习对电竞行业的推进作用，使得电子竞技越来越科学化，也为其提供更多的理论支持。

在文章剩余部分将介绍以下几方面内容，一、用于分析电竞角色选择的模型，主要介绍有序Lasso-Logistic模型，简要概述逻辑回归模型、Lasso模型、SVM模型、梯度提升决策树模型；二、描述文章采用的数据集，包括变量、数据特征等以及数据处理；三、分析有序Lasso-Logistic模型的变量选择；四、将有序Lasso-Logistic模型的预测结果与其他模型的预测结果进行比较并分析，得出结论。

2 模型介绍

2.1 Binary Logistic Regression模型

二项逻辑回归模型是处理因变量是二分类问题的回归模型[16]，在分析个人信用评估、医学诊断、地质灾害危险区划分等方面常用到。假设对于自变量的观测矩阵X,因变量的观测向量y,第i个观测值表示为(xi,yi)；i=1,2,…,N；xi=(xi1,xi2,…,xip)；yi=0或者1,那么关于X的线性回归模型可表示为：

g(x)=β0+xβ

(1)

将上式结合Sigmoid函数：

(2)

得逻辑回归模型如下：

(3)

p(X)=P(y=1|X)表示给定X时y=1的条件概率,β0,β是模型的参数，其绝对值越大，相应的自变量越重要，参数符号为正，表示自变量与因变量y=1的条件概率P(y=1|X)呈正相关，符号为负，则表示自变量与因变量y=0的条件概率P(y=0|X)呈正相关。逻辑回归模型一般采用极大似然估计法进行估计，以下式子中用pi(x)表示p(xi)=P(yi=1|xi)，由于观测值(xi,yi)的似然函数是：

pi(x)yi[1-pi(x)]1-yi

(4)

所以N个观测值的似然函数就是：

(5)

对上式取对数似然函数及其相反数：

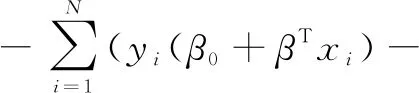
log(1+eβ0+βTxi))

(6)

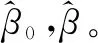
2.2 Lasso-Logistic模型

Lasso(Least absolute shrinkage and selection operator)[17]近年来发展十分迅速，不仅在理论方面，在实际应用上也是如此，特别是在处理变量很多的情况下或者稀疏性变量矩阵的处理上展现出明显的优势。Lasso通过构造罚函数让一些变量的系数值等于零从而实现压缩估计，既可以简化模型又可以避免过拟合，在如今的大数据趋势下显示出更重要的作用。Lasso的最小二乘形式目标函数如下：

(7)

将上式结合式(6)可得Lasso-Logistic模型[10]的目标函数如下:

(8)

在式(7)和式(8)中，λ≥0是可调整的参数，它的大小与β的稀疏性有关，通过调整λ的大小以筛选变量。

2.3 有序Lasso-Logistic模型

有序Lasso模型是2016年Tibshirani和Suo在文献[18]提出的优化问题并提出了相应的解决算法。该模型是在一般Lasso模型的基础上附加一个关于模型系数绝对值的单调有序约束条件，文献还把有序Lasso模型应用在时间序列问题上，通过仿真数据和臭氧数据等数值实验显示出有序Lasso模型的参数估计值比一般Lasso模型的的参数估计值更接近真实值的良好效果。尽管有序Lasso模型是含有约束条件的模型，但是它更好地利用了自变量与因变量之间的先验信息，所以使得模型的拟合效果胜过一般Lasso模型。另外，有一些文献将有序Lasso模型应用到其他领域，比如Nguyen和Braun[19]将有序Lasso模型结合时间序列问题应用于生物学的基因调控网络，探索基因表达在不同时间点的动态变化，并将模型结合半监督学习法探索出新的调控因子，在基因表达、基因调控网络方面得到不错的结果。该文基于有序Lasso模型[17]将其应用于因变量是二分类的数据上，充分利用了先验信息，显现出自变量对因变量(P(y=1|X))的不同影响并取得了良好的预测效果，体现了含有单调有序约束条件的Lasso问题在分类问题上的实际应用价值。

有序Lasso-Logistic模型可看作是有序Lasso模型[18]的扩展，由Lasso-Logistic模型的目标函数式(8)结合有序Lasso模型[17]得到有序Lasso-Logistic模型如下：

(9)

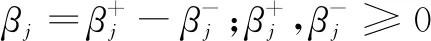
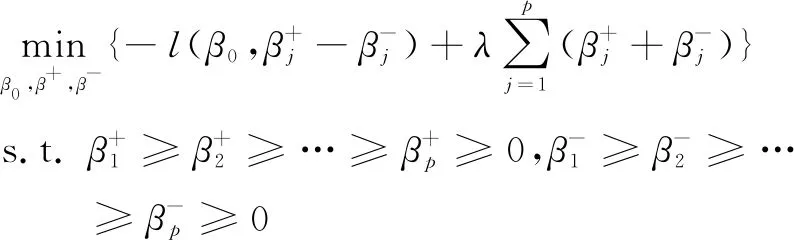
(10)

对于改进后的目标函数(10)将通过子问题式(11)求解，子问题如下：

(11)

其中:

X是N×p的自变量观测矩阵，y是N×1的因变量观测向量，p是由pi,i=1,2,…,N组成的向量。

2.4 SVM模型

SVM(support vector machine)模型[20]也是一种二分类模型，通过构建一个超平面或超平面集，使得两类样本中离超平面最近的样本间隔最大化，这些超平面对应的向量就被称为支持向量。支持向量机可以进行线性分类和非线性分类，在解决小样本，非线性及高维模式识别中表现出许多特有的优势，但不太适用于较大的数据集，且不易选出正确的核函数，其目标函数是：

式子中yi={0,1},(xi,yi)是一对观测值，w是超平面法向量，b是超平面的截距。

2.5 Gradient Boosting Decision Tree (GBDT)模型

梯度提升决策树模型(GBDT)是一种迭代的决策树算法，由多棵决策树组成，是广义梯度提升模型(Generalized Boosted Regression Model)(GBM)其中的一种，所以同样是将弱学习器变成强学习器的一种方法且基于boosting算法，而boosting算法是一种可用来减小监督式学习中偏差的机器学习算法，大多数由许多基础的分类模型组成，进行迭代后根据不同模型分类的准确率给予权重，产生一个较复杂的分类模型，借此强化模型的分类准确率。由于模型是由多个基础分类模型构成，所以可以避免过拟合的情况，可用于回归问题和分类问题，泛化能力和表达能力都很好，具有较好的可解释性，有更高的性能上限，但只能处理低维稠密的数据，对高维稀疏的数据表现较差，处理类别特征效果没有数值特征好。

3 数据集分析

3.1 数据集来源与数据处理

该文通过UCI机器学习库获取一份在线游戏刀塔2的数据集，该数据集是2016年8月份玩家进行刀塔2在线游戏的记录。每一个观测为一局游戏记录数据，每一局的游戏时间不超过两小时。数据变量如表1所示，包括获胜队伍，cluster ID(与玩家服务器位置有关)，游戏模式，游戏种类以及113个英雄的id总共117个变量。

表1 变量说明

由表1可看出，刀塔2数据集包含了9种游戏模式和3种游戏种类，几乎涵盖了所有五对五的队伍比赛模式和种类。该文重点在于探索不同角色选择对比赛的获胜结果的不同影响，所以将数据集中表示比赛结果的获胜队伍变量作为因变量y,其他变量作为自变量，除cluster ID外其余均为分类数据变量，其中id为28、112、117三个自变量与其他自变量存在共线性所以给予剔除。刀塔2游戏每一局都会有一个cluster ID，选定一种游戏模式和一种游戏种类，敌对双方各选五个英雄进行战斗，每一局游戏中一个英雄只能被选择一次。将进行战斗的两个阵营分为1阵营和-1阵营，因此在每个观测值中有五个id变量等于1和五个id变量等于-1代表此局被选中的英雄，而其他没有被选中的id变量取值为0。

y取值1表示1阵营取胜，取值-1表示-1阵营取胜，为了方便模型分析，将游戏结果获胜队伍的值-1改为0，即yi={0,1}，-1阵营选取的英雄id仍取值-1。所有的观测值中没有缺失值，每个观测值有114个变量，只有其中的13个变量的数据取值非零，其余的变量均等于0，可知此数据集所形成的矩阵是一个稀疏性较强的矩阵，且自变量较多。该文主要考察不同角色对游戏获胜结果P(y=1|X)的影响，因此暂不考虑不同英雄间的作用，并且通过计算各id变量间具有高度相关性(变量间相关性绝对值的阈值为0.75)的变量数量发现其值为零,显然在这个数据集中只考察单个英雄对获胜结果的影响是较合理的。为了比较有序Lasso-Logistic模型在不同样本量中与其他模型的预测表现，该文采用了三个样本量(N=2 000,N=3 000,N=6 000)的数据进行分析，并对所有模型进行五折交叉检验后计算出平均准确率(ACC值)和平均ROC曲线下方面积值(AUC值)，在三个样本集中分别随机取1 600个，2 400个，4 800个样本作为训练集，剩余400个，600个，1 200个样本作为测试集。在三个样本量的数据中，1阵营获胜的局数分别是1 051局，1 588局，3 209局，-1阵营取胜的局数分别是949局，1 412局，2 791局，可见样本数据集分布比较对称，不存在一方阵营获胜局数远远多于另一方阵营的情况。

3.2 有序Lasso-Logistic模型变量选择

Lasso在R语言中很容易通过加载glmnet程序包和lars程序包调用相应的函数进行模型分析，所以该文主要介绍有序Lasso-Logistic模型的变量选择，选出样本集N=2 000其中的一个训练集进行变量筛选分析。

有序Lasso-Logistic模型的有序性约束条件主要通过关于自变量的先验信息所得，获取先验信息的方法不一，可以是在收集数据时结合实际问题根据经验和专业知识对自变量与因变量之间的关系有所了解而得之，也可以通过计算变量间的相关性或者进行模型分析后对自变量进行重要性排序获得。总之，有序性约束条件反映的是自变量对因变量(分类数据中是对因变量P(y=1|X)不同的重要性和影响程度。该文在有序Lasso-Logistic模型中约束条件的先验信息是通过逻辑回归模型结合变量重要性排序所得，因主要考察各个英雄与获胜队伍y=1的关系并且表1中前4个自变量对于每一局游戏都是必不可少的变量，所以主要对id变量的重要性进行由大到小排序，以此获得所需的先验信息作为模型的有序约束条件。经实验，不同样本量可能会使得对变量的重要性排序稍有差异但并不会有很大的变动。

变量筛选在有序Lasso-Logistic模型中由含有参数λ的惩罚项控制，λ≥0的是可以调整的参数，惩罚项通过调整λ值实现压缩系数从而筛选变量的过程，不仅使模型复杂程度降低，也可以避免过拟合。λ取值不同产生的模型也不同，取值越大对模型的惩罚力度越大，模型获得的变量越少，最终λ会在某个取值上使得模型获得最佳性能和较少的变量。该文通过λmin=5*10-4λmax(R orderedLasso程序包)选取λ的取值范围(λmax值与数据集的大小有关)，选择50个不同的λ值，用交叉验证法进行计算，选择出均方误差(MSE)最小的λ值作为最优模型的参数值。

图1是有序Lasso-Logistic模型分析训练集N=1 600的样本量数据对应λ的不同取值与相应模型的变量数目变化。在图的上方横轴是变量数目，左边纵轴是不同λ值相应的估计误差MSE，中间的两条灰色线位于左边的线是估计误差值最小对应的λ值(lambda.min)，所得到的模型性能最佳，右边的线是lambda.min在一个标准差范围内既维持了良好的模型性能又能使变量数达到最少的λ值(lambda.1se)。从图中可以看到，在λ=lambda.min时变量数是106个，而在保持模型良好性能的情况下，变量数可以筛选至83个。

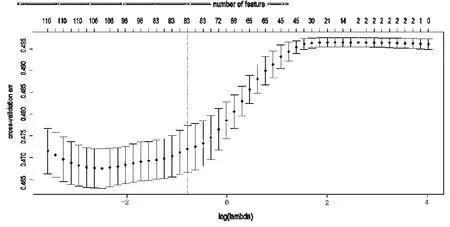
图1 lambda和变量数目的变化

图2是随着λ值的变化，自变量系数发生变化的过程，从图中可看出一些变量的系数估计值随着λ增大逐渐被压缩至零，结合图1这些系数相应的变量将被剔除，只留下含有非零系数的变量，有序Lasso-Logistic模型随着λ逐渐增大，非零系数在逐渐减少，变量数在逐渐减少，由此实现模型的压缩估计，筛选出一部分的变量。

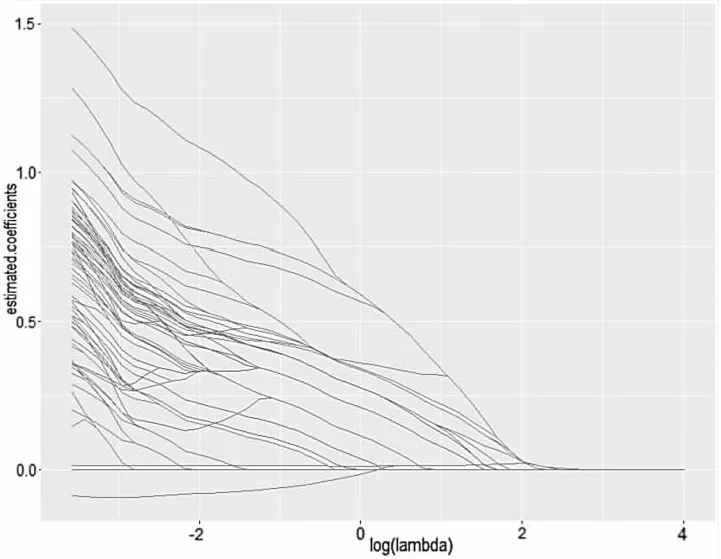
图2 lambda系数路径变化

3.3 预测结果与模型比较

所有计算过程均在R-3.5.3进行，其中逻辑回归模型采用的stat程序包里的glm函数估计模型参数，SVM模型调用的是e1071函数，Lasso先采用cv.glmnet函数用五折交叉验证法得到lambda.min,再用glmnet函数结合lambda.min得系数估计值，GBDT模型则是采用gbm函数进行参数估计，其中用交叉验证法确定最佳迭代次数并调用coord函数得到最佳临界值以此确定预测的类别。将有序Lasso-Logistic模型与另外四种机器模型对三个不同的样本数据进行五折交叉验证并计算预测结果的平均准确率ACC值和平均AUC值。从计算结果看出，有序Lasso-Logistic模型在三个不同的样本量中ACC值和AUC值均比其他四个模型高。表2是不同的样本量中有序Lasso-Logistic模型与其他模型预测结果对比ACC和AUC值高出的最小值和最大值差异(逻辑回归模型用LR表示)。

表2 预测结果差异表 %

从表2可知，在样本量N=2 000时模型预测结果差异比较大，有序Lasso-Logistic模型的平均AUC值比其他模型最高高出9个百分点，最低也高出4.5个百分点，平均准确率ACC值高出4个百分点左右。随着样本量增加，有序Lasso-Logistic模型预测结果比其他模型高出的差异有所减小但仍表现出一定的优势。在表2中，与有序Lasso-Logistic模型预测结果产生最小差异的分别是逻辑回归模型和Lasso模型，产生最大差异的是SVM模型和GBDT模型。由此可以看出有序Lasso-Logistic模型的预测结果和模型的性能的确比其他模型好。为了更加直观地比较各个模型的性能表现，作出ROC曲线如图3～图5所示。

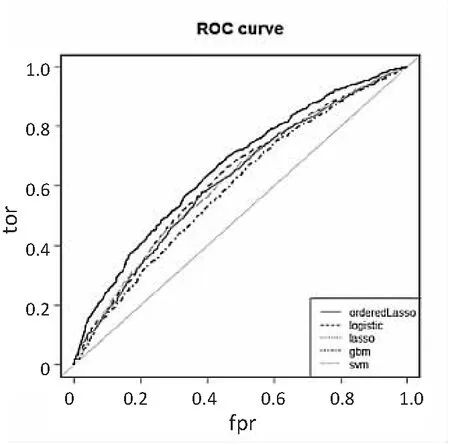
图4 ROC曲线(N=3 000)

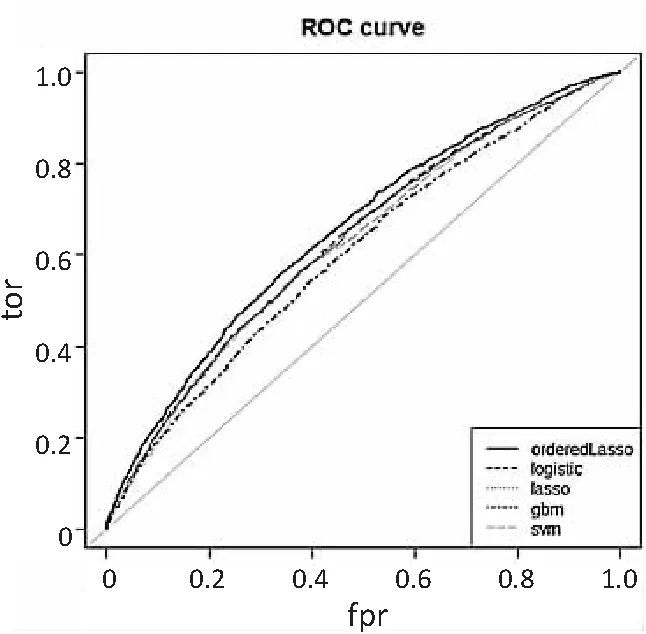
图5 ROC曲线(N=6 000)

逻辑回归模型在三个样本量中的预测结果是其他四个机器学习模型中最好的，仅此于有序Lasso-Logistic模型。在处理二分类因变量数据集时，逻辑回归模型必然是首选，其优点不言而喻，不仅容易解释和实现，而且计算速度快，但是发现在自变量很多的情况下容易使结果变得不准确，这很有可能是因为变量过多而产生一些过拟合的现象。Lasso模型的预测结果与逻辑回归模型不相上下，正好可以弥补逻辑回归的缺陷，在处理变量较多，特别是变量矩阵具有稀疏性的情况下展现很强的优势，但是从实验结果来看会发现，在模型变得简练的同时也产生了一些误差，损失了一些准确性。从两个模型的预测结果和优缺点出发，添加了有序约束条件进行预测，预测结果得到明显提高，即改进后的模型的确是更好。另外两个分类器模型SVM模型和GBDT模型在分类数据上也得到广泛使用，然而在此数据集预测结果较差，原因之一很可能是数据的稀疏性导致，特别是GBDT模型。

该文通过分析刀塔2数据集并把预测结果与其他四种常见的机器学习模型进行比较，可以看出有序Lasso-Logistic模型的预测结果比其他模型准确率高，模型的性能更好。不仅如此，从有序Lasso-Logistic模型还可以通过有序约束条件推测出刀塔2的英雄id对比赛获胜结果的不同影响。表3是对获胜结果影响比较大的变量系数估计值，表4是对获胜结果影响比较小的变量系数估计值。

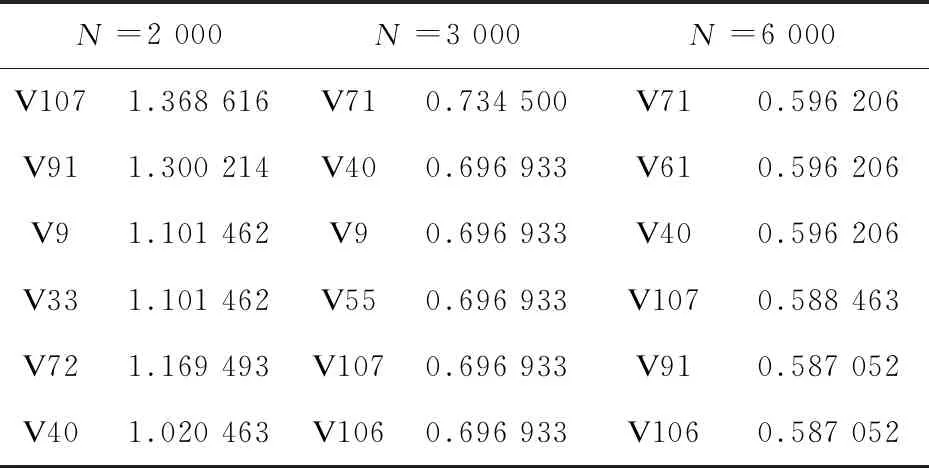
表3 重要性较强的变量及其系数

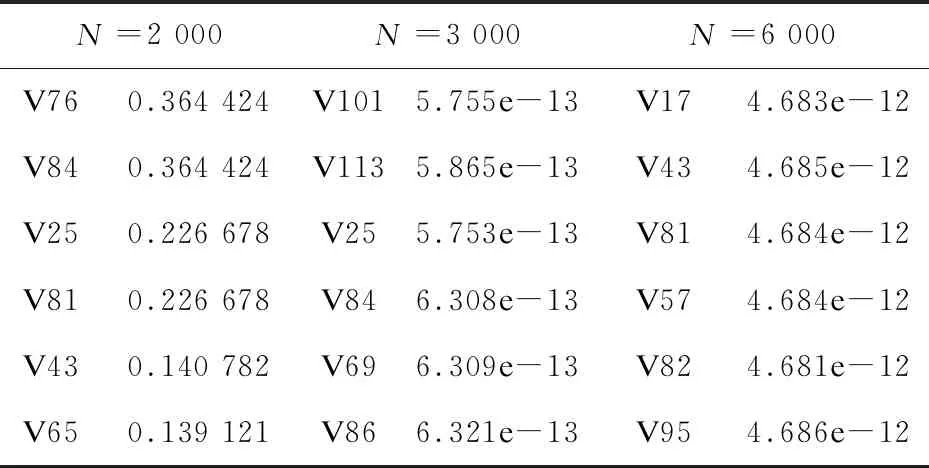
表4 重要性较弱的变量及其系数

从表中综合有序Lasso-Logistic模型对不同的样本量的刀塔2分析所得，一些英雄如id是61，71，13，9，107，55，40，41，106，107等英雄对获胜结果的影响始终比较大，而id是56，17，93，43，111，65，25，115，62，86等英雄对获胜结果的影响比较小，对获胜结果影响比较大的那些英雄在所有观测中使用的频数并没有明显较高，所以推测可能是更容易操作或者杀伤力更强。同样，在其他电子竞技上，那些表现出对获胜结果影响比较大的角色可以令选手更加侧重考虑，在阵容构建上提供一定的参考。

4 结束语

该文将有序Lasso-Logistic模型引入到电竞角色选择分析和对结果的预测中，将预测结果与其他四种常见的机器学习模型相比较，最终发现有序Lasso-Logistic模型性能最好，预测准确率最高。有序Lasso-Logistic模型采用了自变量系数绝对值的有序约束条件融合了Lasso-Logistic模型，其中有序约束条件包含了自变量对因变量发生的先验信息，反映了实际应用问题中各个自变量与因变量P(y=1|X)之间的不同重要性。主要结论有：首先，有序Lasso-Logistic模型同样适用于多变量数据集和稀疏性矩阵，可以对变量进行压缩估计从而筛选变量。其次，增加了先验信息的有序Lasso-Logistic模型在二分类数据上的表现比逻辑回归模型和Lasso的预测准确率更高，模型性能更好。最后，电子竞技中不同角色能力存在差异，对取胜结果的重要性也不一样，了解不同角色对取胜结果的不同影响有助于选手在训练或者比赛中考虑角色选择策略而且对角色的选择更有信心，促进电子竞技选手的训练和发展。另一方面，通过有序Lasso-Logistic模型对电子竞技角色的分析不仅仅使得电子竞技上得到数据化发展，也使得机器学习的分类模型得到进一步扩展，有序Lasso-Logistic模型不但可以应用于电竞行业分析，在其他领域分类问题上同样可以充分利用变量的先验信息进行分析以提高预测准确率并提供相应的策略支持。