基于3D打印的钛合金-体心立方球杆结构人工骨支架设计

杨保旭，段明德，张壮雅，刘静波

（河南科技大学 机电工程学院，洛阳 471003）

0 引言

目前，我国人口年龄构成已呈现老龄化趋势，据2015年世界卫生组织统计数据显示，我国骨病患者已多达1.5亿，移植骨的来源匮乏，及自然骨移植术后出现的排异反应，一直是骨科面临的难题。人工骨支架的出现，使得骨组织缺损患者能够完全治愈成为可能[1]。

近年来，随着对点阵结构研究的不断深入，使得在满足力学性能的条件下，设计并制造出规则的微观多孔骨支架结构成为可能[2]。冯辰栋等[3]并对分别采用SLM（选择性激光熔化）以及EBM电子束熔融技术对所创建的金刚石微孔结构进行3D打印，研究了金刚石多孔钛架的微观孔隙结构以及点阵的力学性能，得出通过选择性融化技术得到的微孔结构与设计值更为接近。张钱城等[4]通过研究各种类型点阵材料的单胞结构分析了不同的点阵结构力学性能的差异，并指出了增强点阵结构力学特性的常用方法；Gómez S等[5]采用泰森多边形单胞结构设计了外形类似骨小梁的三维多孔支架，得到能够满足天然骨骼力学性能的支架模型；杨立军等人[6]设计了开口杆状单胞模型，仿真研究了弹性模量和孔隙率随模型参数的分布对单胞结构力学性能的影响；Li等人[7]采用细杆结构构造出多孔单元，并根据密质骨和松质骨的孔隙率不同，分别应用了不同的孔隙率的单元结构。

在众多的多孔点阵结构中，金属点阵是一种兼备轻质、高强度、高刚度和功能多样化潜力的新型结构材料，其中体心正交体由于其托扑类型简单，可靠性好，压缩失效形式单一等优点，使之成为点阵结构的首选[8]。MASKERY等[9]通过理论计算以及试验探究，得出了体心立方点阵结构BCC单胞尺寸大小对其力学性能方面的影响；柏龙等[10]采用解除体心立方（BCC）单胞长宽高三个方向尺寸相等的特性，提出一种体心四方（Body-centered tetragonal，BCT）点阵的一般单胞模型，并通过理论计算论述体心四方结构相比体心立方结构在力学性能上所具有的优势。Ushijima K等[11]，指出体心立方单胞结构的宽度和高度之比越小，并且随着支柱的直径增大，其单胞结构的初始刚度、塑形破坏强度也就越大。

然而传统的体心立方点阵模型，连接强度不高，并且容易在端点交汇处发生断裂，这是因为传统的单胞模型在交点处形成了尖锐过渡，而在节点处造成了一定程度的应力集中现象。基于此，本文提出一种基于体心立方的球杆结构，能够有效的提升点阵结构的力学性能，并解决点阵结构在节点处容易容易遭到破坏的现象。同时端点球的引入也为后续相邻单胞间不同直径支柱的拼接问题奠定了基础。

1 模型建立

1.1 杆状单胞模型建立

体心立方杆状多孔结构，为方便研究及实验样件尺寸要求，本设计采用整体尺寸为1mm正立方体。如下图所示首先将12条棱边以及4条体对角线为轴线，通过对横截面直径为0.2mm的圆在相应的基准面上进行拉伸操作，得到如图1(a)、图1(b)所示的框架结构及杆状单胞模型。对单胞结构进行阵列后，形成杆状点阵结构。由于点阵结构不易于施加载荷与约束条件，因此在顶层和底层圆柱杆的所在平面上，以点阵的中心在该平面的中心为原点，在点阵的基础上设计出方便有限元分析的下端固定面及上端受力面的辅助部分，杆状单胞点阵结构如图2所示。

图1 杆状结构

图2 杆状单胞点阵结构

1.2 顶点球简化模型

体心正交体由于其托扑类型简单，可靠性好，压缩失效形式单一等优点，使之成为点阵结构的首选。然而传统的体心立方点阵模型，连接强度不高，并且容易在端点交汇处发生断裂，这是因为传统的单胞模型在交点处形成了尖锐过渡，而在直径不相等的部分，则由于横截面的不同造成了一定程度的应力集中现象。如图3所示体心立方顶点球的引入，并采用过渡圆角的建模方法，能够较好的解决融合问题，这种方法能有效解决连接处因尖锐过渡而造成应力集中的现象。

1.3 球杆单胞模型建立

在杆状体心单胞的基础上，将立方体的8个顶点分别加上直径0.5mm的球体，以方便相邻单胞间不同支柱的拼接并对节点进行加固。其中球杆结构如图4(a)、图4(b)所示的框架结构及球杆单胞。图5是由上述单胞结构在三方向阵列的点阵结构。

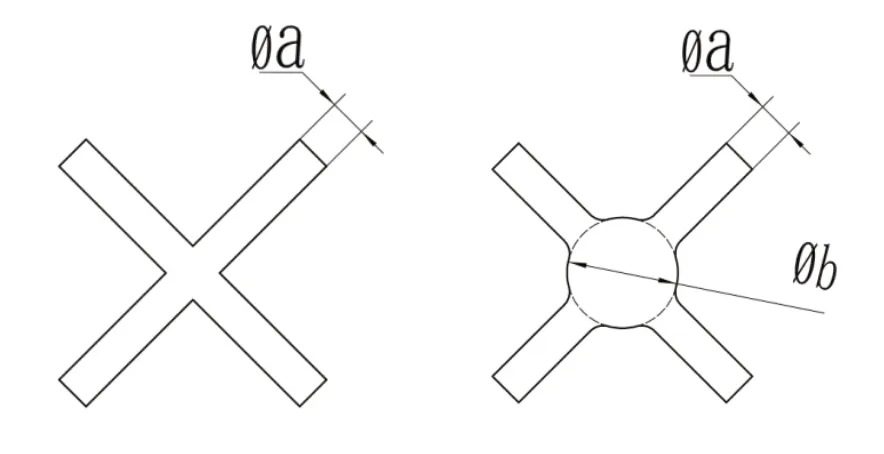
图3 相同直径杆交叉优化前后

图4 球状结构

图5 球杆单胞点阵结构

2 有限元力学性能分析

2.1 材料属性及边界条件

目前常用于承力骨支架制造的材料为钛合金，钛合金不仅具有较优异的力学性能，而且已经被证实无论是在体内还是在体外都具有较好的成骨性能，因此选用Ti6A14V作为研究材料，在有限元分析软件ANSYS18.2中，定义分析材料为钛合金，该材料弹性模量为96GPa，泊松比为0.36，密度为，4620kg/m3。本文进行有限元分析的点阵几何模型，杆径为0.2mm，球杆径比从2.0～3.0变化，网格大小为0.01mm，网格单元划分为四面体网格类型。将几何模型下端固定，上端面加载大小为150N方向上的拉力。

2.2 有限元力学分析

为简化分析计算，在对试样进行拉伸实验时，取拉伸试样中的一部分，作为有限元分析模型，分析模型为3×3×3的点阵单胞模型及辅助板组成。设计四组单胞杆径为0.2mm的几何模型：1）杆状体心立方点阵结构；2）球杆直径比2.0的球杆结构；3）球杆直径比2.5的球杆结构，4）球杆直径比3.0的球杆结构。

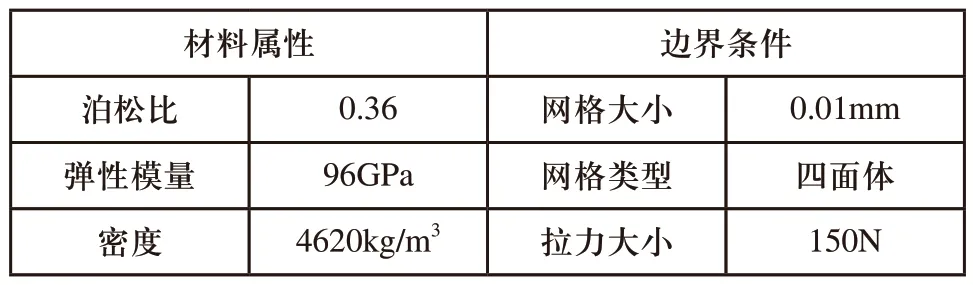
表1 材料属性及边界条件

在ANSYS18.2软件中对上述4个点阵模型进行有限元静力学分析。1）设计体心立方杆状钛合金支架与体心立方球杆结构钛合金骨支架的力学性能对比分析，探究两种不同单胞结构对应的点阵在力学性能上的差异；2）设计三组杆径形同但球杆直径径比值不同的点阵模型，分析比较在不同的球杆直径比值下，点阵的力学性能的变化规律。

图6 杆状点阵应力云图

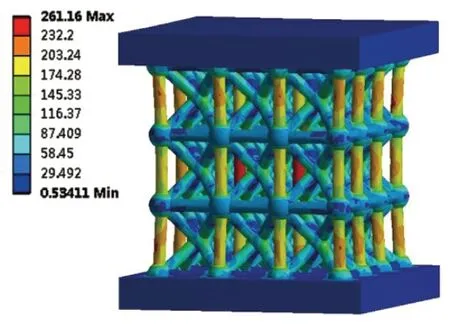
图7 球杆直径比2.0点阵应力

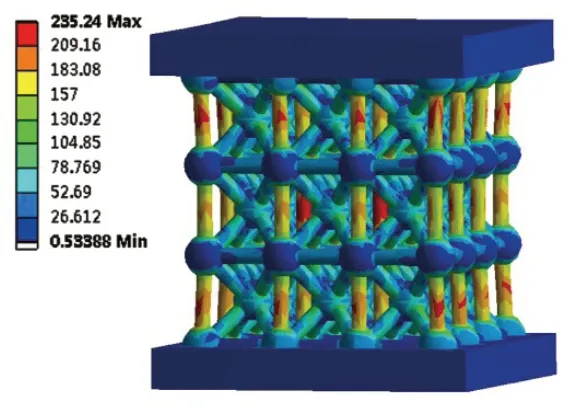
图8 球杆直径比2.5点阵应力

图9 球杆直径比3.0点阵应力

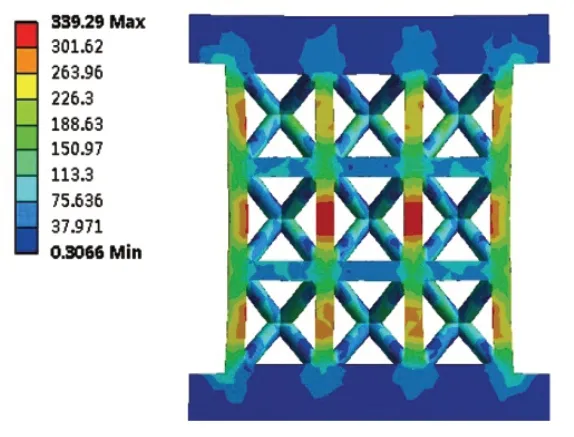
图10 球杆直径比2.5点阵剖面应力

图11 球杆直径比3.0点阵应力云图

分析结果表明：1）节点球的引入能够有效改善点阵结构的力学性能，在有限元模型的边界条件下，杆状体心立方点阵结构的最大应力为339.29MPa，球杆直径比为2.0球杆体心立方点阵结构的最大应力为261.16MPa，应力值降低了23%；2）随着球杆直径比的增加，点阵结构的最大应力值逐渐减小，且直径比从2.0～3.0变化的过程中，球径的增加对应力降低的效果逐渐减小，并且当球杆直径比从2.0～2.5变化时，节点球的引入对点阵最大应力值有着显著的降低作用，球杆直径比从2.5～3.0变化时，点阵结构的应力值仍有一定程度的减小，但是减小的程度有所降低；3）杆状体心立方单胞点阵结构节点处应力为150.97MPa，球杆体心立方点阵结构节点处应力为78.754MPa。

表2 点阵最大应力随球杆直径比变化关系

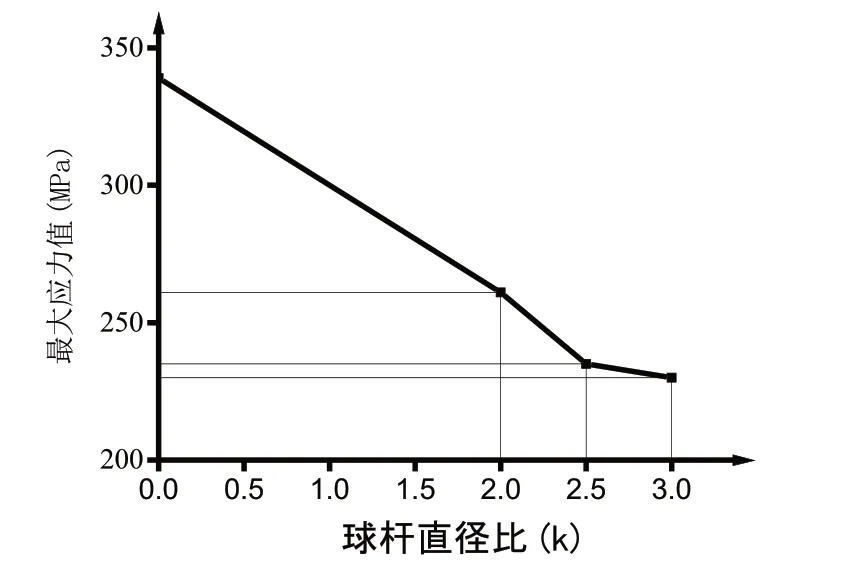
图12 点阵最大应力-球杆直径比变化

3 试验

3.1 样件模型创建

根据实验要求，设计出外形尺寸如图13所示的拉伸试样模型。实验样件主要由3部分组成，两端的夹持部分和中间的测试部分。其中本次实验样件的测试部分，按照单胞结构的不同，分别设计了如图14、图15所示的杆状结构点阵拉伸模型及球杆结构拉伸模型。

图13 拉伸试样外形尺寸

图14 杆状结构试样模型

图15 球杆结构试样模型

按照试样的测试部分3×5×20mm的要求，将得到的体心立方杆状单胞模型进行阵列处理，并采取布尔操作将单个的单胞融合为一体。取代拉伸试样受力部分，完成杆状单胞点阵模型的创建。按照上述方法，完成球杆结构单胞点阵模型的创建。

3.2 试样制备

以Ti6Al4V钛合金粉为原料，通过选择性激光熔化SLM（Selective laser melting）制造出体心立方杆状点阵结构钛合金多孔支架及体心立方球杆结构。根据有限元分析结果，当球杆直径比为2.5时，节点球的引入对点阵的力学性能的影响最佳，因此，本文实验模型选择杆状体心立方点阵结构与球杆直径比为2.5的球杆体心立方点阵结构作为本次对比实验的模型。其中在杆状结构中多孔支架的微孔直径参数设置为0.2mm，在球杆结构中杆径设置为0.2mm，球径设置为0.5mm。分别打印整体尺寸如图7所示的实体拉伸样件，杆状拉伸样件，球杆结构拉伸样件）如图所示的杆状拉伸实验样件以及球杆结构实验样件，其中有效力学实验测试部分为5mm×3mm×20mm的长方体单胞点阵模型。

3.3 力学性能结果分析

由图14可见，分别将得到杆状点阵实验及球杆点阵实验样件实验得到的的应力应变曲线放入同一组图中进行比较。

通过压力与拉伸样件的横截面的比值得到应力，绘制出点阵的应力-应变曲线。如图所示为两种不同的单胞结构组成的点阵，取曲线的最高点得到抗拉强度。通过应力应变曲线我们可以发现球杆结构的抗拉强度要高于杆状点阵结构的抗拉强度。

球杆点阵结构的力学性能优杆状BCC参照结构，其极限屈服强度将近达到BCC参照结构的1.5倍，球杆点阵结构的刚度和强度方面表现出了明显优势，这与有限元分析趋势一致。

图16 拉伸试样应力应变曲线

3.4 断口结果分析

将样品置于金属载物台上喷金处理后，利用场发射扫描电镜（Nova 400）和配套的能谱仪（IE350PentaFETX-3）观察分析样品的表面及断口形貌。

如图17、图18所示为拉伸试样的电镜图分析结果。由断口电镜图分析可得，体心立方球杆结构断裂面主要发生在节点处，并且在节点处发生断裂破坏。而球杆结构的断裂面主要发生在杆上，因此在球杆结构中顶点球的引入能够有效解决点阵结构在节点入容易发生断裂的现象。

图17 杆状体心立方点阵结构断口

图18 球杆体心立方点阵结构断口

4 结语

本文提出的球杆结构，通过在点阵节点处增加节点球，从而是点阵的不同杆在交汇处进行固结及融合，通过对杆状单胞点阵结构以及球杆单胞点阵结构进行有限元分析得出如下结论：

1）节点球的引入，能够有效降低点阵结构的应力，提高点阵的整体力学性能使得点阵结构得到优化。

2）当球杆直径比为2.5时，节点球的引入对点阵的力学性能的影响最佳。

3）节点球的引入，对节点起到保护作用，这为后续不同直径的拼接奠定了基础。