粗糙表面弹性微动接触数值研究

赵三星，吴 桐，阮金华

（武汉科技大学冶金装备及其控制教育部重点实验室，机械传动与制造工程湖北省重点实验室，湖北 武汉 430081）

1 引言

微动是指二表面的微小振幅的运动，这种接触情况在大多数有振动的机械工程中经常出现，会导致接触界面的微动磨损，而磨损是零件损坏或设备失效的主要原因之一。所以对微动接触的研究并如何减小或者避免磨损具有非常大的参考价值。

微动接触大部分的解析解和数值解局限于同质接触问题。文献[1]得到了同质物体微动接触的解析解。在此基础上，文献[2-3]最早用数值方法进行耦合求解异质微动接触问题，得到了刚性平底压头接触数值解。文献[4]首次对二维异质微动接触进行数值方法求解文献[5]提出了三维接触模型，研究了不同材料之间的部分滑移行为。在微动接触的数值研究中需要一种准确且有效的算法来计算。共轭梯度法CGM（Conjugate gradient method）的提出[6]可以有效解决法向力、切向力同时存在的接触问题。通过使用共轭梯度法并结合快速傅立叶变换，许多摩擦接触问题的计算效率和准确性得到了显著提升。

目前，对微动接触的的理论和算法研究主要集中在光滑表面上，缺少考虑粗糙度影响的粗糙微动接触研究。在验证算法正确的基础上，考虑粗糙度将正弦表面和非高斯表面加在接触表面对三维微动接触进一步研究，解决异质粗糙表面两接触体的三维微动接触问题，并对接触压力、切向应力等进行比较研究。

2 微动接触理论与模型

微动接触模型，如图1（a）所示。此时，固定法向力W，切向载荷Fx随时间进行周期性变化。

沿x方向，如果A1和A2的绝对位移（相对于点O）的滑移距离以Sx1和Sx2表示，由式（1）确定[1]，如图 1（b）所示。

式中：下标 1，2—物体 1 和物体 2；ux1、ux2—表面变形；δx1、δx2—刚体位移。沿x方向A1和A2之间的滑移分量可以写成[1]：

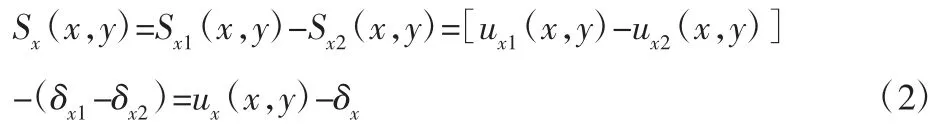
同理也可以得到y方向上的相对滑移。

在一个局部滑移接触问题中，接触模型[1]可以由（3）表示：

式中：ux、uy、uz—平行于x，y和z方向的变形；δx，δy，δz—接触体在x，y和z方向的刚性位移；Sx、Sy—沿x和y方向的相对滑移距离；g—表面间隙；h0—接触体的几何形状。

表面弹性变形通过影响系数并利用FFT 方法求解，式（4）表示为：

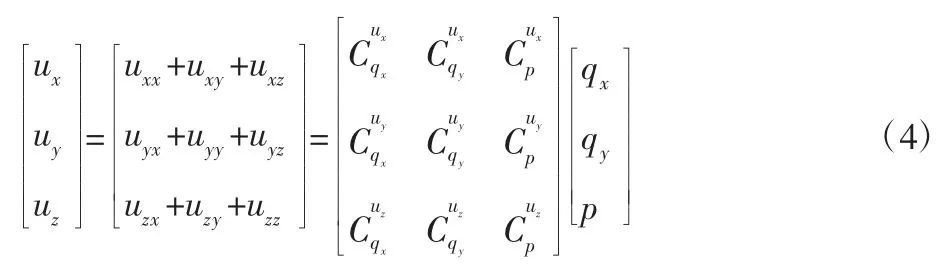
在数值分析中，式（3）可以分为两部分。一个是用来解决法向接触问题，表示为：

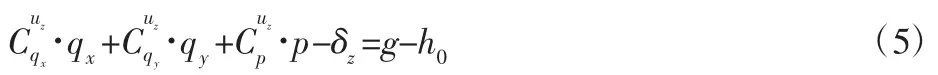
另一个是用来解决切向接触问题，可以写成如下：

在微动接触模型中，切向力Fx随时间周期性变化。由于界面存在摩擦，求解结果和加载路径相关，即接触应力状态不仅取决于外加载荷，而且与加载的时间历程有关。

为考虑加载路径的影响，需将接触求解公式改成和加载路径相关的微分形式。若两接触体弹性特性不同，则法向接触求解和切向接触求解相互耦合。下文建立与加载路径相关的法向和切向接触求解模型。

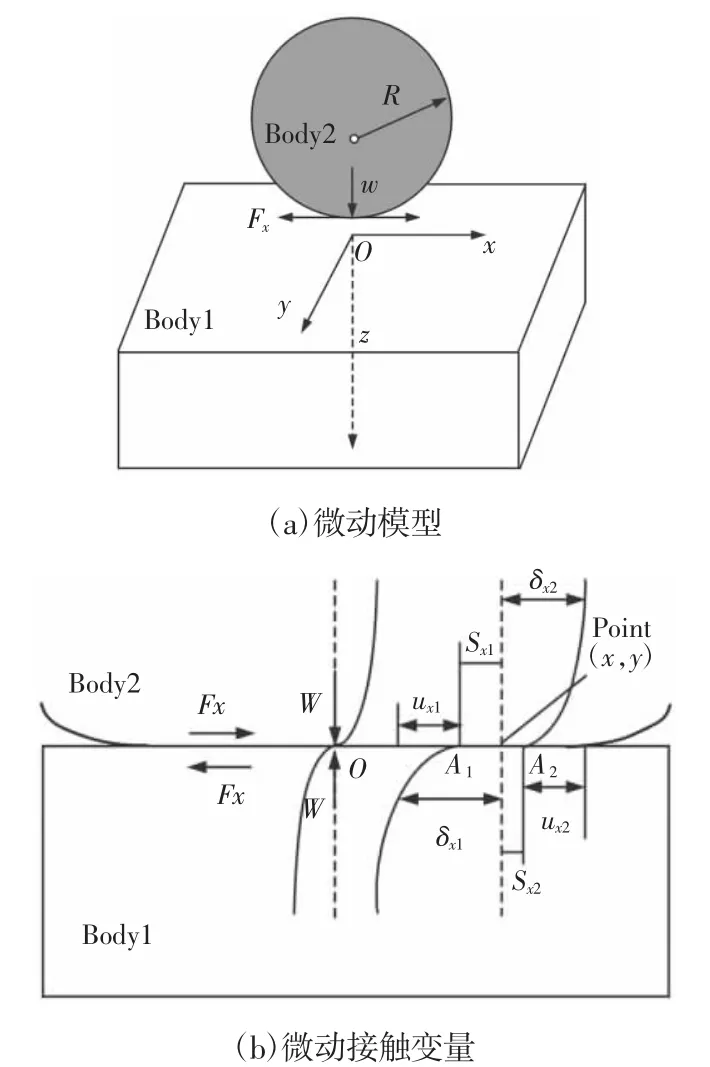
图1 三维接触微动模型和接触变量Fig.1 3D Contact Model and Variables Under Fretting Conditions

2.1 法向接触求解

在t时刻的Kuhn-Tucker 的补充条件[1]：

式中：gt—t时刻表面垂直间隙。式（5）可以重写为：

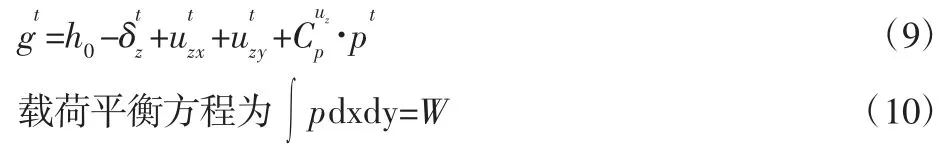
式中：W—法向载荷。变形通过切向接触求解，此时方程（9）变为未知压力的线性方程组，并通过边界条件（7），（8）使用CGM 有效地求解压力p。

2.2 切向接触求解

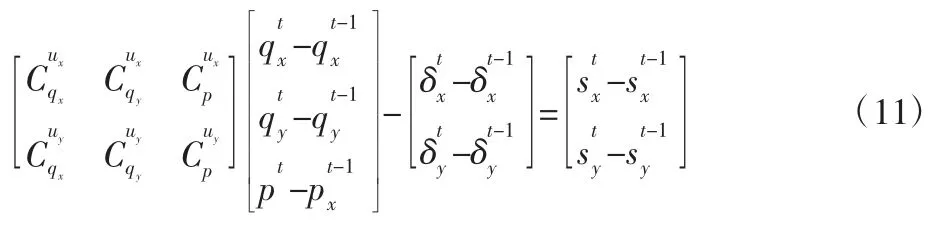
式中：上标t，t-1—第t时刻和t-1 时刻的值。在求第t时刻的切向应力时，需要用到t-1 时刻值，而t-1 时刻的值在上一时间步中求解得到。零时刻的初始值相应的，t时刻切向应力在粘着区域和微滑区域遵循如下条件[1]：

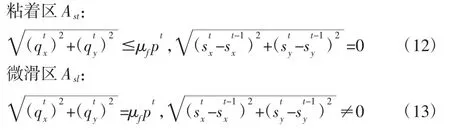
通过求解式（11）和相应的边界条件（12）、（13）得到切向应力。只不过此时求解的是第t时刻的值，而第t-1 时刻的值为已知。t时刻切向应力求得后，切向应力引起的法向变形便可通过影响系数的方法求得，然后返回式（7）～式（9）求解新的pt。新的pt带入式（11）求解新的切向应力直到迭代收敛。

3 计算结果与比较

3.1 算法验证

本节数值求解同质微动接触问题，接触参数，如表1 所示。此时考虑接触表面为光滑表面，接触体的弹性特性相同。计算区域为-1.5a≤x≤1.5a，-1.5a≤y≤1.5a，网格数目取 256×256。震荡力Fx加载在接触表面，如图2 所示。得到同质微动切向应力qx和解析解的对比图，如图3 所示。解析解计算公式见文献[1]。可见两种结果吻合，说明本算法可精确求解微动接触问题。

表1 输入参数Tab.1 Input Parameters

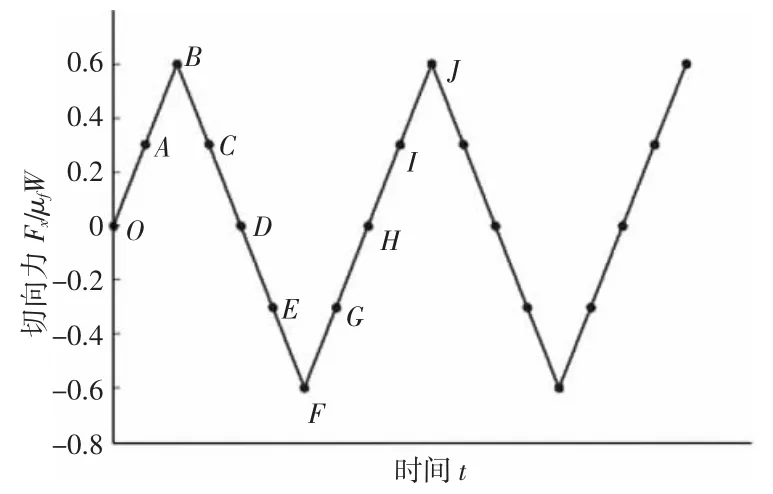
图2 切向力FX 的变化Fig.2 Tangential Load Path

图3 切向应力qx 沿x 轴分布（解析解和数值解对比）Fig.3 Shear Traction qx Distributions Along the x

3.2 光滑异质表面微动接触分析

本节分析光滑异质表面微动接触问题，前文中所研究的微动接触是同质表面，对于异质表面接触求解来说，同质微动接触的算法同样适用。只是将接触模型中弹性球体改为刚性球体，接触表面摩擦因数 μf等于 Dundurs[1]常数 β，取 μf=β=0.28571。其它的与同质微动参数一致，如表1 所示。

不同时刻下的接触压力，可以看出不同的切向力Fx对法向接触压力的影响较小，如图4（a）所示。不同时刻下的切向应力，如图4（b）所示。对于同质微动接触，如图3 所示。B时刻和F时刻的切向应力qx大小相等，方向相反；经过一个周期后，切向力分布将重合。但对于异质微动接触，由于材料特性等一些参数的影响会有所不同，如图4 所示。B时刻和F时刻的切向应力qx分布没有类比性；经过一个周期之后B、J两个时刻的切向力分布也不同。

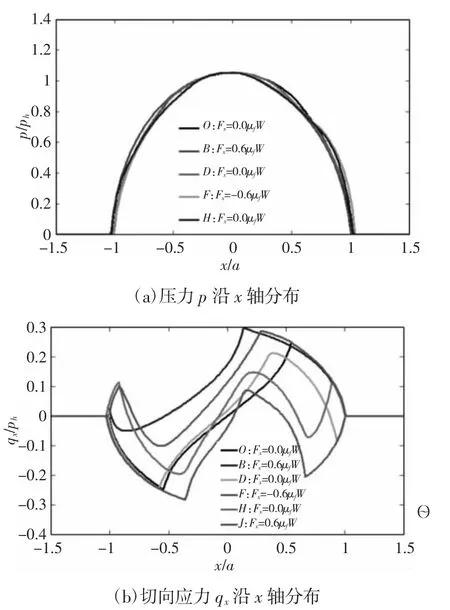
图4 异质微动接触的接触压力和切向应力分布Fig.4 Contact Pressure and Tangential Stress Distribution of Heterogeneous Fretting Contact

3.3 粗糙表面异质微动接触分析

3.3.1 正弦粗糙表面

为了研究粗糙表面对微动接触的影响，本节考虑在半无限体上叠加正弦粗糙表面，接触模型，如图1 所示。其他参数跟光滑异质微动接触一致。正弦粗糙表面公式如下所示：

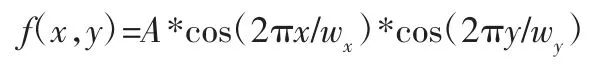
式中：A=0.8μm—正弦波幅值；wx=wy=0.5a—波长，a—Hertz 接触半径，计算区域为-1.5a≤x≤1.5a。

-1.5a≤y≤1.5a，网格数目为 256×256。

不同时刻，压力p和切向应力qx沿x轴分布图，如图5 所示。切向应力分布均呈现出尺寸效应，即，单个粗糙峰上切向应力分布呈现和光滑表面接触类似的形状。如图在B时刻的qx和微滑接触中的qx对比显示，（这里的微滑接触见文献[8]，它与微动接触的不同在于Fx为固定值，因此在这里，结合文献[8]将两者进行了对比研究）。如图5 可以看出在微动接触中，位于x轴负方向粗糙峰上的qx分布相对陡峭。这是由于，在微动接触中切向力需要分布加载，而微滑接触中的结果是一次加载得到的。

图 5 O，B，D，F 时刻，压力 p 和切向应力 qx 沿 x 轴分布Fig.5 Pressure and Shear Traction Distributions at Points O，B，D and F

3.3.2 非高斯粗糙表面

在实际工程中遇到的表面都是随机粗糙表面，研究发现，这些粗糙表面大都服从非高斯分布。采用文献[9]的方法可生成接近于实际工况的非高斯表面。本算例采用各向同性粗糙表面，x和y方向的波长 βx和 βy都为 20μm，RMS 为 0.1μm，粗糙表面的偏态Sk=0.5，峰度K=5，如图6 所示。将上述非高斯表面叠加到微动接触模型中。4 个时间点的切向应力分布情况，如图7 所示。可以看出粗糙表面的切向应力变化趋势与异质光滑条件下的形状，如图4（b）所示。其值绕着光滑表面上下波动，由于粗糙峰的存在，粗糙表面下的最大切向应力要比光滑条件下的大。对于粗糙表面来说，最大表面应力是机械零部件的界面损伤和寿命设计的重要指标。

图6 非高斯粗糙表面 Sk=0.5，K=5Fig.6 Non-Gaussian Random Rough Surface Sk=0.5，K=5

图 7 B，D，F，H 时刻，切向应力 qx 沿 x 轴分布Fig.7 Shear Traction Distributions at Points B，D，F and H

4 结论

利用共轭梯度法计算法向和切向载荷同时作用下的异质粗糙表面微动接触，并用快速傅立叶变换对卷积计算进行加速，经过数值研究得到如下结论。（1）微动接触的求解结果和加载路径相关。对于同质微动接触问题，切向应力的分布经过一个周期会重合，趋于稳定。而异质微动接触中由于材料特性、参数不同没有类似的规律。（2）在正弦粗糙表面接触中，切向应力分布呈现出尺寸效应。（3）在非高斯表面接触中，得到的切向应力与在异质光滑条件下的形状相似，其值绕着光滑表面上下波动。由于粗糙峰的存在，粗糙表面下的最大切向应力要比光滑条件下的大。