线控转向系统变角传动比设计及路感模拟

王晓峰，汪选要

（安徽理工大学机械工程学院，安徽 淮南 232001）

1 引言

线控转向系统取消了转向盘和转向轮之间的机械连接，改用线连接，布置更加自由[1-2]。目前线控转向系统的变角传动比设计大多是利用控制算法将变角传动比设计成与横摆角速度、与车速以及与转向盘转角的函数或从汽车横摆角速度增益不变和侧向加速度增益不变的角度出发设计变角传动比[3-4]。考虑到车辆转向灵敏度随车速变化的变化特性，根据车辆的转向灵敏度和车速确定了变角传动比设计依据。线控转向系统的路感是由模拟产生，目前对路感的模拟主要有传感器测量，动力学模型估算，参数拟合等方法[5-7]。上述三种方法都能够对路感进行模拟，但没有对驾驶员偏好、道路的变化、及参数的获取进行综合考虑。综合考虑“人-车-路”闭环系统的路感获取，因此采用权重法对路感进行模拟。

2 二自由度模型的建立

二自由度模型建立，在车辆坐标系中，我们忽略车辆沿着ox轴的速度u的变化，认为车辆只有沿着oy轴的侧向运动和绕oz轴的横摆运动两个自由度。整车部分参数，如表1 所示。

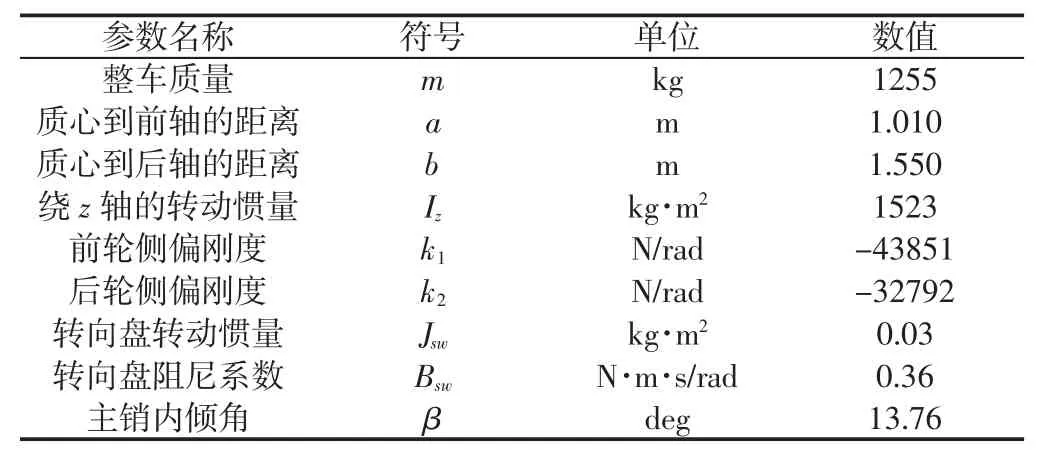
表1 整车部分参数Tab.1 Vehicle Section Parameter

二自由度车辆运动微分方程[8]表示为：

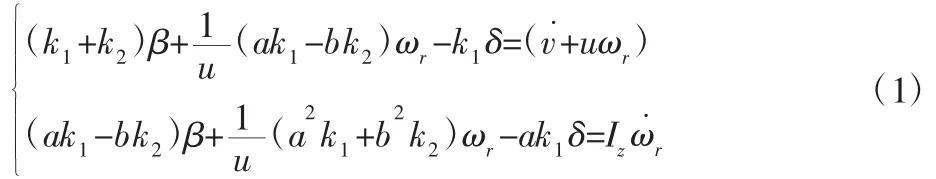
式中：β—质心侧偏角；v—质心速度在车辆坐标轴oy轴上的分量；u—质心速度在车辆坐标轴ox轴上的分量；δ—前轮转角；ωr—汽车横摆角速度。

车辆的质心侧偏角可式（2）表示：

横摆角速度增益为：

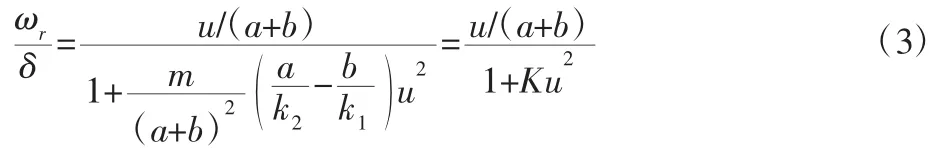
式中：K—稳定性系数。

3 变角传动比设计

3.1 理想变角传动比

机械转向系统车辆转向系统的角传动比基本都是固定值，车辆的转向特性一般是随车速变化而不断变化，所以驾驶员就需要不断对转向特性进行补偿，增添了驾驶负担。如果要改善车辆转向特性，就传动比方面可以把传统的固定角传动比设计为随车速变化而变化的变角传动比。因此基于转向灵敏度不变，把角传动比设计为仅随车速变化的特性曲线，如图1 所示。

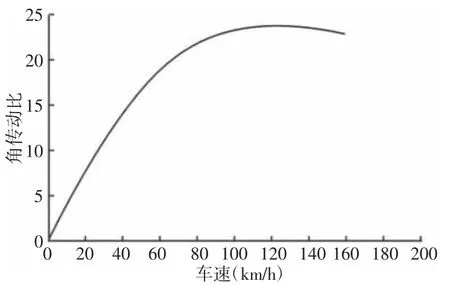
图1 变角传动比特性曲线Fig.1 Variable Steering Ratio Characteristic Curve

汽车的稳态横摆角速度可表示为：

3.2 变角传动比修正

结合实际情况，车辆在低速行驶情况下如果角传动比很小，即使驾驶员给转向盘一个小的转角信号都可能使得前轮产生一个相对较大的转角，使得转向过于灵敏，驾驶员就会对前轮转角进行不断的调整，增添了驾驶员的忙碌程度。所以设置了最小传动比imin，选取30km/h 为临界车速此时角传动比设为最小值imin=11，得到式（6），并得出传动比特性曲线，如图2 所示。

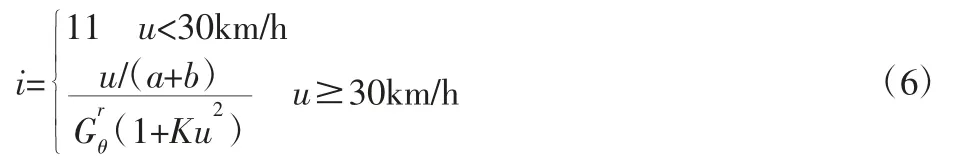
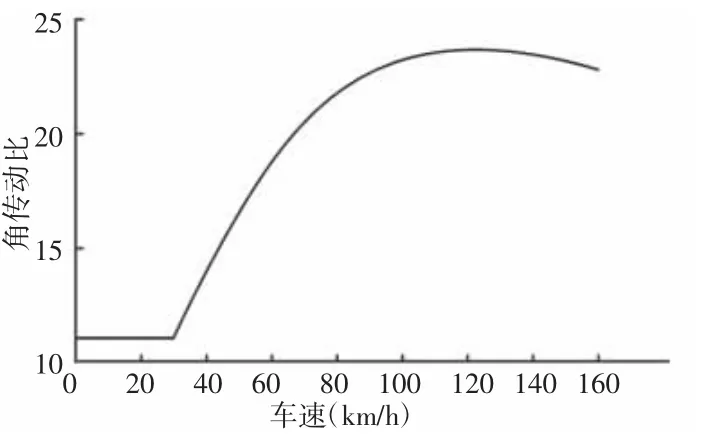
图2 修正后的变角传动比特性曲线Fig.2 Adjusted Variable Steering Ratio Characteristic Curve

3.3 转向灵敏度随车速变化特性

采用在不同车速下转向盘角阶跃输入，观察转向灵敏度的变化来验证所设计的变角传动比特性。在simulink 搭建好的二自由度模型中给转向盘一个幅值为80°的角阶跃信号，得到不同车速下的转向灵敏度变化曲线，如图3 所示。

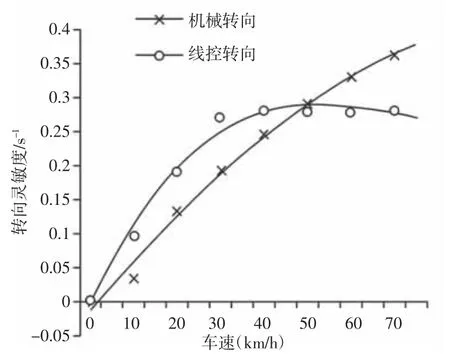
图3 转向灵敏度随车速变化曲线Fig.3 Steering Sensitivity Varies with Vehicle Speed Curve

低速转向工况下，机械转向系统车辆的转向灵敏度较小，转向不灵敏，车辆响应较慢。在大转角转向的情况下，驾驶员需要大幅度转动转向盘来获得前轮所需要的转角才能让车辆按照期望的路线行驶，这时驾驶员的操作负担较重。采用变角传动比设计的车辆的转向灵敏度在低速转向阶段大于机械转向系统车辆的转向灵敏度，转向时车辆响应较快，因此驾驶员不需要较大幅度转动转向盘就可以达到同样的转向效果，减小了驾驶员的操作负担。

高速转向工况，机械转向系统车辆的转向灵敏度较大，转向过于灵敏。在车速很大时，很小的一个前轮转角都会引起车辆路线的很大程度偏移，机械转向系统车辆在高速情况下，转向盘很小的转角都会对路径产生很大的影响，路况复杂时甚至会发生危险情况，驾驶员在此过程精神较紧张。采用变角传动比设计的车辆在高速转向阶段转向灵敏度明显小于机械转向系统车辆的转向灵敏度，增大了驾驶员转动转向盘的范围，从而减小了驾驶员操作时的紧张程度。

4 路感模拟

4.1 路感模拟的方法

路感是驾驶员转动方向盘时感受到的方向盘反馈的作用力或转矩。该力或转矩包含了车辆运动状态，轮胎受力情况及路面等信息。目前路感模拟方法主要有参数拟合法，动力学模型估算法和传感器测量法。参数拟合方法是根据中国驾驶员的偏好[9]，将反馈力矩设计成与转向盘转角，车速，侧向加速度关的函数形式。文献[10]中将总的反馈力矩设计成两部分，第一部分影响因素是车速和转向盘转角，第二部分影响因素是车速和侧向加速度，并进行权重设计。考虑到路感是模拟产生及车辆行驶时车速、转向盘转角和侧向加速度的关系，所以把路感反馈设计如下式所示：

式中：TN—转向盘反馈力矩；Tsw—车速和转向盘转角拟合的转矩；Tay—车速和侧向加速度拟合的转矩。

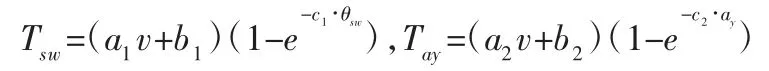
式中：θsw—转向盘转角；v—车速；av—侧向加度。

基于动力学模型估算的方法，根据车辆动态响应和驾驶员转向盘输入，通过车辆动力学模型估算轮胎回正力矩和所需的反馈力矩。

不考虑转向系统的内部摩擦进行反馈力矩估算，轮胎型号选为205/55R16。该轮胎拖距产生的回正力矩估算值表达式为：

式中：e—轮胎拖距；m—整车质量；v—车速；m1—前轴载荷；m2—后轴载荷；k1—前轮轮胎侧偏刚度；k2—后轮轮胎侧偏刚度；L—轴距；δ—前轮转角。

主销内倾产生的回正力矩M2表达式为，

式中：Q—轮荷；D—主销偏移距；β—主销内倾角。

虑到转向系的阻尼和转动惯量，得到的总的转向盘力矩为：

式中：T—转向盘反馈力矩；is—转向传动比；As—助力系数；Jsw—转向盘总成转动惯量；Bsw—转向盘总成阻尼系数。

传感器测量方法，利用力矩传感器测量齿条处的力矩，该力矩包含有轮胎力和回正力矩及路面等信息。

4.2 权重法模拟路感

在车速分别为10km/h 和80km/h 在对开路面工况下给转向盘幅值为350°的角正弦信号输入，对上述方法进行仿真，仿真结果，如图 4、图 5 所示。

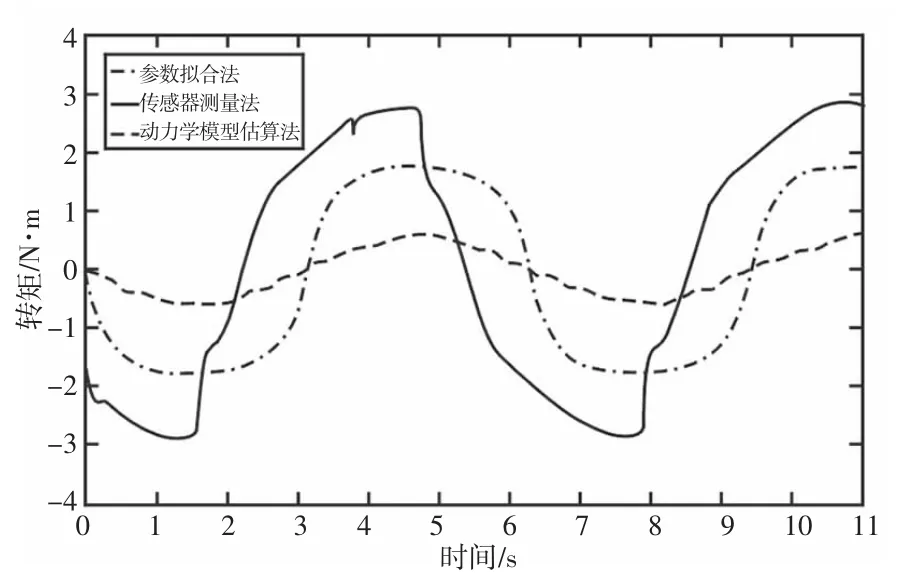
图4 车速为10km/h 时模拟转矩曲线Fig.4 Simulated Torque Curve at 10km/h

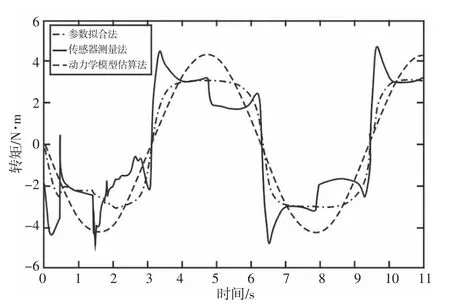
图5 车速为80km/h 时模拟转矩曲线Fig.5 Simulated Torque Curve at 80km/h

对图4、图5 结果进行分析可以看出，上述三种方法都能够对路感进行模拟，但是都存在不足之处。

传感器测量方法，该方法模拟的路感较为真实，充分考虑了道路信息和车辆状态，但是对驾驶员的关注不够。参数拟合方法，该方法充分考虑了驾驶员的偏好，但是人对路面的变化信息获取不够，驾驶员不能及时获取有效信息。基于动力学模型计算的方法，该方法虽然简单，成本低。但是获得准确的参数相对较难，估算的力矩并不准确。

从图4，图5 可以看出随着车速的增大，反馈力矩对于路面的变化变的敏感，驾驶员需要通过转向系的反馈的力矩的获取路面的变化信息。

综上，考虑到“人-车-路”的相互关系，结合驾驶员偏好与转向系统对道路信息的获取以及车辆的行驶状态，用权值法对路感进行模拟，如下式所示：

式中：TC—传感器测量的转矩；T—转向盘反馈力矩；K—权值。

车速越高时转向力矩受到路面的影响越明显，此时应该重点考虑道路信息获取，车速较低时人和车对路面的变化要求较低，此时应该重点考虑驾驶员偏好。所以在进行路感设计时应该在低速时关注度偏向于驾驶员，在高速时关注度偏向于道路信息的获取。以此为依据来确定权值。

假定权值的大小与车速成线性关系且最高车速v为160km/h得：

在上述条件下车速为35km/h 进行仿真结果，如图6 所示。

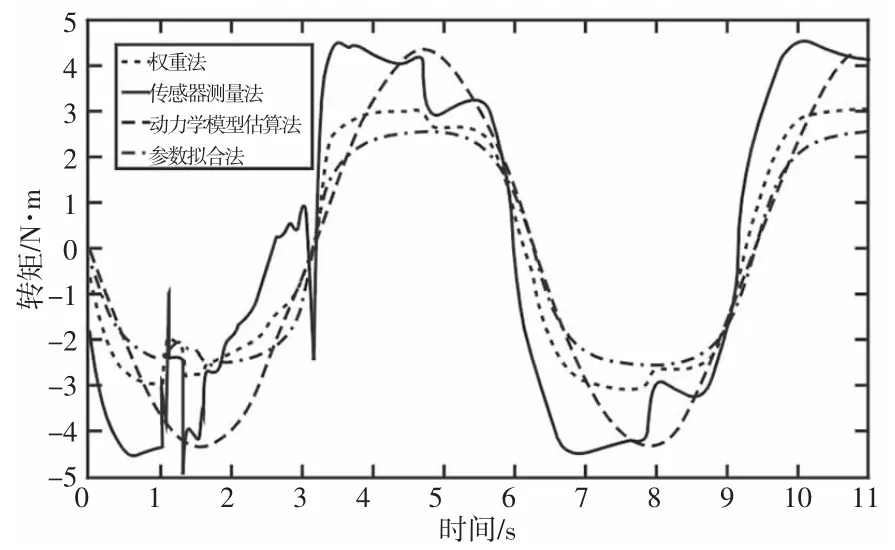
图6 车速为35km/h 时模拟力矩对比曲线Fig.6 Simulated Torque Curve at 35km/h Speed

从图6 可以看出权重法在相同的条件下转向系统既考虑到了驾驶员偏好的转向力矩，又能够对路面的变化作出相应的反馈，能够很好的模拟路感。

5 仿真试验

5.1 双移线试验

为了验证上述设计的线控转向系统的操纵稳定性，进行了双移线试验，线控转向车辆采用与机械转向车辆相同的转向盘转角输入，双移线试验相关标准参照ISO 标准[11]实验时车辆以80km/h的车速驶入实验道路，试验结果，如图7 所示。

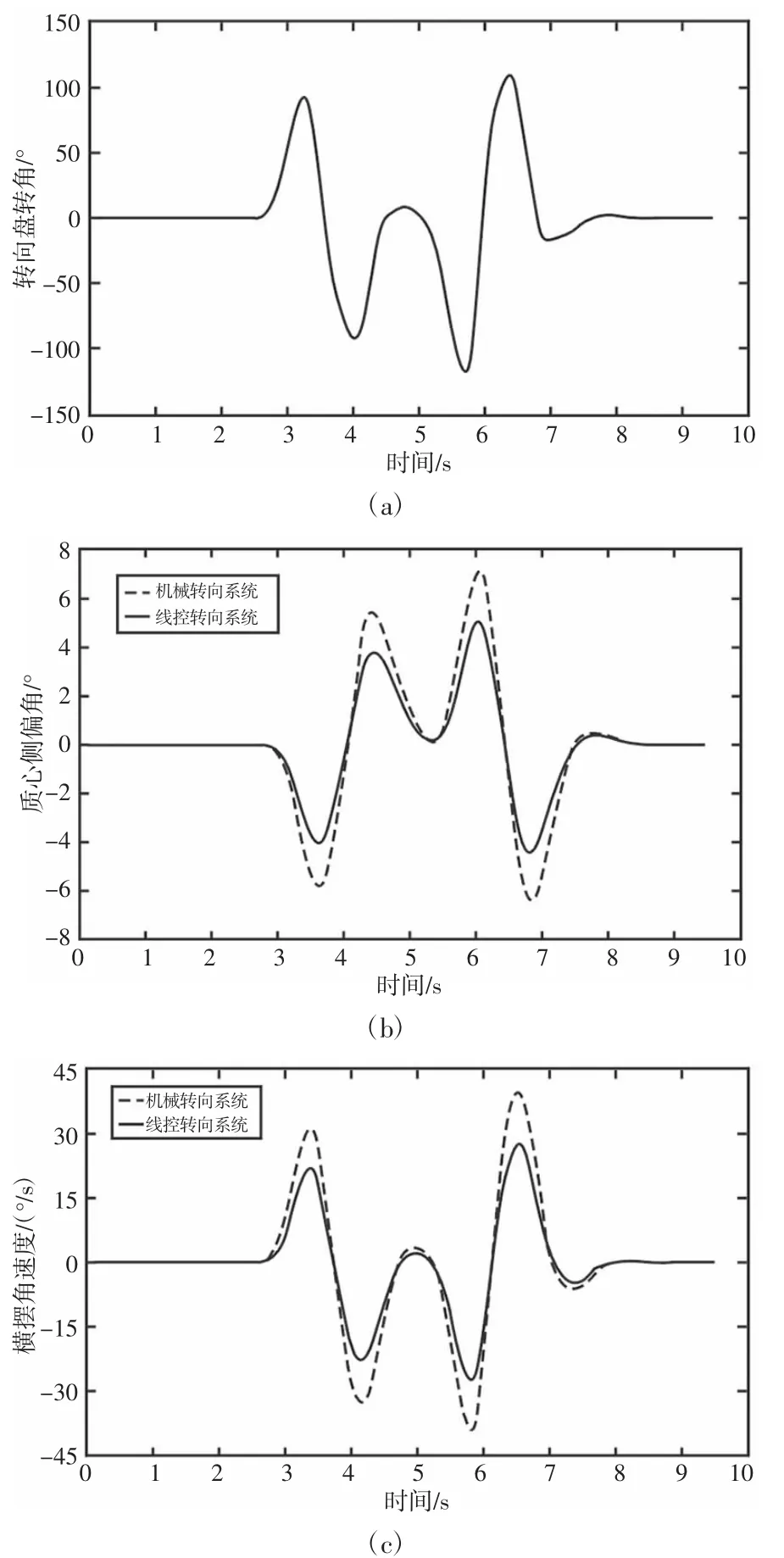
图7 双移线试验结果Fig.7 Results of Double-Line Change Test

从图7 中可看出，车速较高时，在相同的转向盘输入下，线控转向车辆的质心侧偏角和横摆角速度皆小于机械转向车辆，结果说明采用定转向灵敏度的变角传动比设计的转向系统在操纵性、稳定性方面优于定传动比设计的机械转向系统。

5.2 双纽线试验

为了验证上述设计的线控转向系统的转向轻便性，选取双纽线试验，实验时车辆以10km/h 的车速驶入实验道路，试验标准参照国家标准GB/T6323.5-1994 试验结果，如图8 所示。由图8可以看出线控转向系统的转向盘转矩的平均值和最大值显然小于机械转向系统的转向盘转矩，说明了权重法的路感控制策略能够减轻驾驶员的操纵负担，提高转向的轻便性。

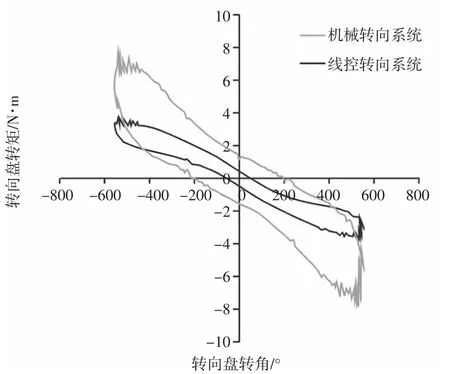
图8 双纽线实验结果Fig.8 Results of Lemniscate Test

6 结论

采用定转向灵敏度的变角传动比设计的线控转向系统在操纵性、稳定性方面优于定传动比设计的机械转向系统。用权重法对路感进行模拟兼顾了驾驶员偏好的转向力矩和路面信息的变化，能够很好的模拟路感，并且提高了转向轻便性。