中央扣对大跨悬索桥颤振稳定性的影响
李凯,韩艳†,蔡春声,2,樊中武,林超
(1.长沙理工大学土木工程学院,湖南长沙 410114;2.路易斯安那州立大学,路易斯安那巴吞鲁日LA70803;3.湖南省高速公路集团有限公司湘西分公司矮寨大桥桥隧管理所,湖南吉首 416000)
大跨悬索桥往往伴随着柔度大、阻尼低等特点[1],很容易受到交通、风及地震等动态环境荷载的影响,采取适当的措施来控制动态载荷作用下的结构响应是其最重要的问题之一.此外,对于典型的不设置中央扣的悬索桥,在动力荷载作用下主缆与加劲梁的位移不同步甚至反向,时常导致悬索桥短吊杆弯曲及断裂的现象发生.因此,在悬索桥的主缆和加劲梁跨中处设置中央扣联结开始广泛应用于大跨悬索桥中,它能够在一定程度上防止跨中短吊杆的弯曲和断裂,抑制结构动态位移响应,提高结构的力学性能.另外,中央扣的设计和使用可以追溯到New Tacoma Bridge的建设[2],中央扣的使用能提高桥梁的抗风稳定性.正是由于中央扣具有以上优点且构造简单,使其成为大跨度悬索桥的一种发展趋势,但中央扣对颤振性能的影响机制仍是不明确的,因此探究中央扣的设置方式对悬索桥颤振稳定性的影响能够为日后中央扣在大跨度悬索桥中的广泛应用提供参考价值,具有重要意义.
近年来,我国已有多座悬索桥采用中央扣结构,相关的文献报道多集中于中央扣对悬索桥固有模态和抗震性能的改变,而关于中央扣对悬索桥抗风稳定性的影响则鲜有报道.徐勋等[3-4]等基于有限元分析发现中央扣能够明显提高悬索桥一阶反对称扭转和纵飘振型的频率.Qin等[5]也采用有限元法得到了与上述类似的结论.胡腾飞等[6]通过矮寨大桥气弹模型动力测试研究发现反对称侧弯频率随中央扣刚度的增大而增加,中央扣能够提高悬索桥的整体刚度,其中以反对称扭转和纵向振动频率提升最为显著,进一步验证了上述基于有限元分析的部分结论.此外,彭旺虎等[7]通过理论研究发现主缆弹性刚度与主缆重力刚度、加劲梁刚度之和的比值决定了第一阶对称扭转和反对称扭转振型的形态和排列次序,中央扣刚度和跨中缆梁间距是影响反对称扭转基频大小的主要因素.在中央扣对悬索桥地震响应的影响研究方面,Wang[8]和徐勋[4]等发现中央扣可以减小由地震激发的主梁端部的纵向位移但会增加塔顶的纵向位移及塔底的弯矩.另外,Wang等[9-10]基于车桥耦合振动分析发现中央扣对行车舒适性指数几乎没有影响.Wang等[11-12]通过抖振计算分析发现当风速为10~40 m/s时,中央扣能显著减小主梁抖振竖向位移和主塔的纵向位移.然而,采用时域分析方法研究中央扣对大跨度悬索桥颤振稳定性的影响,国内外鲜有文章报道.
本文以矮寨大桥为工程背景,采用悬臂梁位移法建立了大桥等效单主梁有限元模型;考虑了跨中短吊杆(无中央扣)、一对柔性中央扣、三对柔性中央扣和刚性中央扣4种结构形式,计算分析了中央扣对大跨度悬索桥自振特性的影响;基于试验获得的颤振导数,采用脉冲响应函数结合Roger有理函数并利用非线性最小二乘拟合方法拟合其系数从而得到主梁断面自激力的时域表达式;随后利用ANSYS二次开发,实现了大桥颤振稳定性时域分析,研究了中央扣对颤振临界风速、颤振频率及主梁三维颤振姿态的影响规律.研究结果可为日后中央扣在大跨度悬索桥中的广泛应用提供参考.
1 有限元建模及动力特性分析
1.1 工程背景
矮寨大桥是一座跨越深山峡谷的单跨悬索桥,主缆矢跨比1 ∶9.6,两主缆形心间距为27 m,主缆孔跨布置为242 m+1 176 m+116 m,加劲梁全长1 000.5 m,主跨跨中附近设置三对柔性中央扣,其中中央扣关于主梁跨中不对称,如图1(a)所示.主梁为钢桁加劲梁,桁宽27 m,桁高7.5 m.钢桁架主梁上采用钢纵梁与混凝土桥面板相结合的桥面体系,横断面布置如图1(b)所示.
1.2 有限元模型
为了准确获得矮寨大桥的动力特性,首先采用有限元计算软件ANSYS建立大桥空间桁架主梁有限元模型,其中钢桁加劲梁与主塔采用beam188梁单元模拟,主缆和吊杆采用Link10杆单元模拟并设置为仅有拉伸刚度.钢-混组合桥面体系采用梁-壳单元混合有限元建模的方法建模,其中混凝土桥面板采用Shell63壳单元模拟,钢纵梁采用Beam188梁单元模拟,同时对梁-壳单元采用MPC方法进行耦合连接.有限元模型及其笛卡尔坐标系如图2所示.由其计算得到的矮寨大桥动力特性列于表1中.为大幅提高颤振时域分析的计算效率并方便准确地对有限元模型施加自激力荷载,基于主梁各方向整体刚度等效的原则,采用悬臂梁单位荷载位移法[13]建立了等效单主梁有限元模型(即鱼骨梁模型).空间桁架主梁模型与等效单主梁模型动力特性结果对比如表1所示,两者主要相应振型的频率误差基本都在1%以内,仅一阶反对称侧弯振型频率误差约为1.7%,因此可以采用等效单主梁模型进行颤振时域分析.

图1 矮寨大桥桥型布置Fig.1 The sketch of Aizhai Bridge

图2 矮寨大桥空间桁架主梁有限元模型Fig.2 The refined spatial-truss-girder model of the Aizhai Bridge
1.3 中央扣对动力特性的影响

表1 空间桁架主梁模型与等效单主梁模型动力特性对比Tab.1 Comparison of dynamic characteristics of the two finite element models

表2 跨中处主缆与加劲梁不同联结形式的4种有限元模型Tab.2 Four different finite element models with different connection modes near mid-span

图3 四渡河悬索桥中央扣的基本构造(单位:mm)Fig.3 Central buckle of Sidu River Bridge(unit:mm)

图4 模型FM-D刚性中央扣有限元模型Fig.4 Rigid central buckle of model FM-D
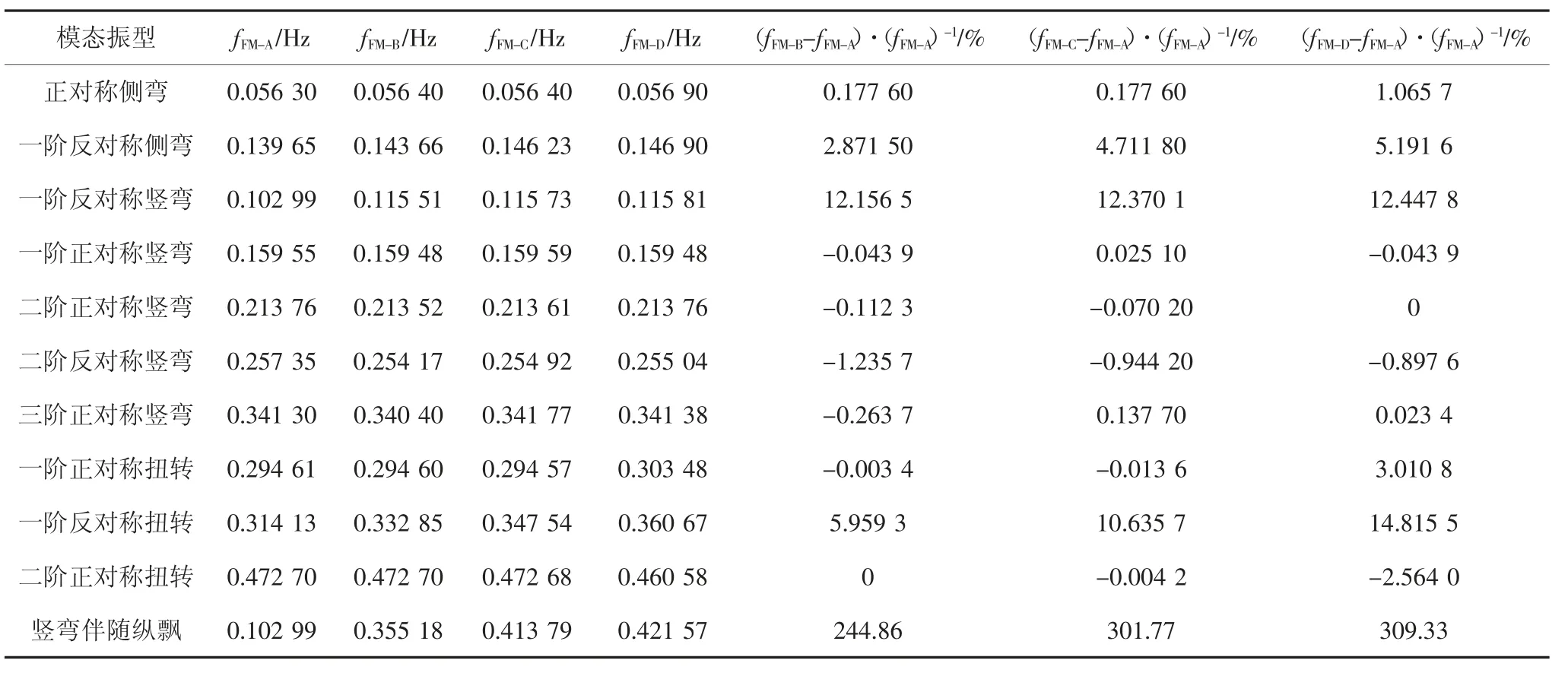
表3 4种有限元模型动力特性对比Tab.3 Comparison of natural mode among four different finite element models
由表3中4种有限元模型自振频率与振型特征的分析比较可以发现:1)由于中央扣的倾斜拉杆能够一定程度限制主缆与加劲梁之间的相对运动,相当于加劲梁在跨中位置被施加了纵向位移约束进而显著提高了主梁的纵向刚度,因此FM-A的纵飘振型伴随一阶反对称竖弯振型出现,频率为0.102 99 Hz;而FM-B、FM-C、FM-D的纵飘振型都伴随三阶反对称竖弯振型出现,频率分别为0.355 2 Hz、0.413 8 Hz、0.421 6 Hz,由此可见中央扣能够大幅提高大跨度悬索桥纵飘振型的频率并提高与其耦合的竖弯振型的阶数,且刚性中央扣的提升幅度最大.2)相比于正对称侧弯振型的频率,反对称侧弯的频率受中央扣的影响明显偏大.3)竖弯振型的频率受中央扣的影响很小主要是由于中央扣仅提高了主梁跨中位置的局部竖向刚度.4)正对称扭转振型频率受中央扣的影响较小,其中刚性中央扣能够提高3%一阶正对称扭转振型的频率.3种中央扣都能够大幅度提高反对称扭转振型的频率,以一阶反对称扭转振型为例,相比FM-A,有中央扣结构的FM-B、FM-C、FMD频率分别提高了5.9%、10.6%、14.8%,可见刚性中央扣提升幅度更大,因此刚性中央扣的抗风稳定性能更佳.
2 颤振稳定性分析
从上一节的分析中发现中央扣对反对称振型的影响要明显大于正对称振型,但其他模态对颤振的贡献需进一步分析,且中央扣对于整个结构的非线性尤其是几何非线性[14]的影响是未可知的.因此,中央扣对柔性主梁颤振行为的实际影响需进一步采用颤振时域分析的方法定性定量地探讨.
2.1 颤振时域分析方法
桥梁结构在均匀流中的运动方程可以描述为:


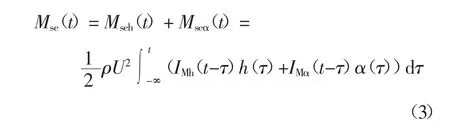
式中:Lsex(x=h、α)代表相应位移产生的气动升力;Msex(x=h、α)代表相应位移产生的气动扭矩;Ifx(f=L、M,x=h、α)为脉冲响应函数.以竖向位移产生的气动升力为例(忽略由第三项加速度项引起的气动力),其最终纯时域表达式为[16]:
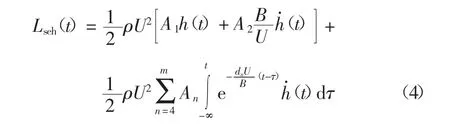
式中:A1、A2、An、dn(n=4,5,…,m)为用近似连续函数Roger有理函数连续表达离散的颤振导数时待拟合的系数[16],可采用最小二乘法拟合确定[17],本文不再赘述.矮寨大桥0°风攻角下节段模型颤振导数试验值和用有理函数近似连续表达反算的颤振导数拟合值对比如图5所示,可见试验值与拟合值吻合得很好.
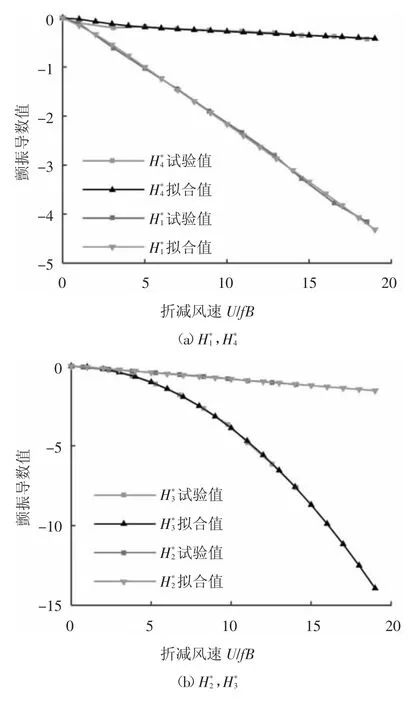
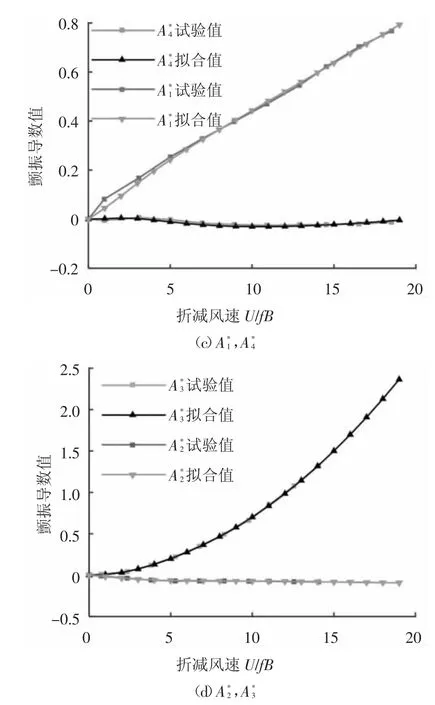
图5 0°风攻角下颤振导数试验值与拟合值比较Fig.5 Simulation versus experimental values of flutter derivatives under 0°wind attack angle
基于自激力时域表达式通过ANSYS APDL语言编写自激力数值计算程序,实现大桥颤振时域分析,其中式(4)中的卷积积分项在计算程序中需转化为数值递推关系式.计算程序采用Newmark-β 法求解式(1)运动方程,通过时间步长无关性检验后计算时间步长取0.01 s.最后,通过逐步提高风速,观察节点位移随时间变化的特性,便可得到结构颤振临界风速.
2.2 不考虑结构阻尼
钢桁梁桥的结构阻尼比一般取0.5%[18].然而,现存很多钢桥的实测结构阻尼比小于0.5%,甚至只有0.2%~0.3%左右.因此,为充分研究中央扣对大跨悬索桥颤振稳定性的影响同时比较结构阻尼对颤振临界风速的影响,本文对不考虑结构阻尼和考虑结构阻尼进行了分析研究.
表1中:va为飞机平台飞行速度;D为天线方位向口径尺寸;Δθ为天线波束方位向扫描角度范围;θmax为方位波束最大指向角,正侧视工作下有Δθ=2θmax;λ为雷达工作波长;R为作用距离;Ls为方位向波束地面照射范围;Rmax为最大作用距离;Pav为发射平均功率;G为收发天线的增益;σ为目标有效反射面积;K为玻耳兹曼常数;T为接收机温度;Ti为目标驻留时间;η为系统损耗;SNR0为脉冲压缩后的信噪比。
图6~图9为不考虑结构阻尼0°攻角情况下模型FM-C跨中节点位移时程.可知风速74 m/s时竖向和扭转位移整体上既无发散也无收敛的趋势;而风速78 m/s时竖向和扭转位移整体上都有明显的发散趋势.细化计算风速范围74~78 m/s时,发现74 m/s可被认为是该条件下的颤振临界风速.另由图6~图9还可以发现FM-C颤振状态具有明显多频率参与的拍振特性,称为间歇性颤振现象.

图6 FM-C跨中竖向位移时程(U=74 m/s,ζ=0%)Fig.6 Vertical displacement response of FM-C at mid-span(Critical,U=74 m/s,ζ=0%)

图7 FM-C跨中扭转位移时程(U=74 m/s,ζ=0%)Fig.7 Torsional displacement response of FM-C at mid-span(Critical,U=74 m/s,ζ=0%)

图8 FM-C跨中竖向位移时程(U=78 m/s,ζ=0%)Fig.8 Vertical displacement response of FM-C at mid-span(Post-critical,U=78 m/s,ζ=0%)
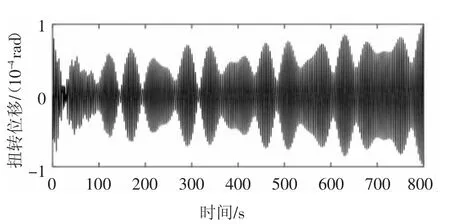
图9 FM-C跨中扭转位移时程(U=78m/s,ζ=0%)Fig.9 Torsional displacement response of FM-C at mid-span(Post-critical,U=78 m/s,ζ=0%)
图10、11分别为风速74 m/s时竖向和扭转位移响应的频谱分析图,可知竖向位移和扭转位移响应具有3个一致的卓越频率.其原因在于该桥在一阶正对称扭转频率附近,密集分布着一些侧弯、竖弯、扭转相互耦合的振型,如图12所示.当主梁发生弯扭耦合颤振时,其颤振频率为0.262 9 Hz,落于上述频率分布密集区,当结构阻尼为0时,极易牵连带动频率分布密集区的振型间歇性参与振动.此外,由图12可知FM-A、FM-B和FM-D的扭转基频附近频率分布也很密集,因此它们的颤振状态也有多频率参与的拍振现象.

图10 FM-C跨中竖向位移响应频谱(U=74 m/s,ζ=0%)Fig.10 Spectrum of vertical displacement at mid-span for FM-C(U=74 m/s,ζ=0%)

图11 FM-C跨中扭转位移响应频谱(U=74 m/s,ζ=0%)Fig.11 Spectrum of torsional displacement at mid-span for FM-C(U=74 m/s,ζ=0%)
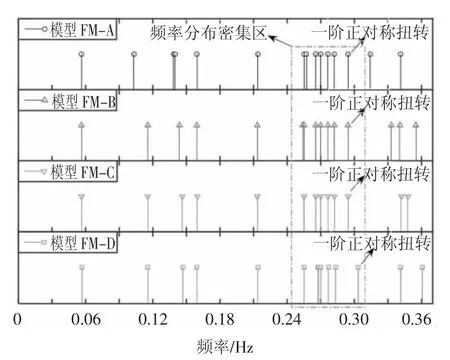
图12 4种模型固有频率分布Fig.12 Natural frequency distribution of four models
表4为4种不同模型颤振临界风速与颤振频率的对比,可知3种不同结构形式的中央扣对颤振临界风速几乎没有影响.
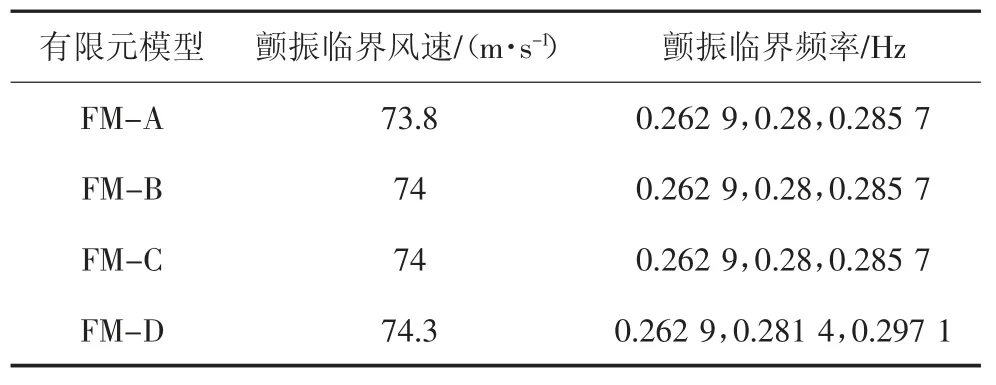
表4 4种模型颤振临界状态对比(结构阻尼比0%)Tab.4 Comparison of flutter critical for four models(ζ=0%)
2.3 考虑结构阻尼
本节首先探讨结构阻尼比对颤振临界风速以及上述间歇性颤振现象的影响.图13为颤振临界风速随结构阻尼比的变化趋势,可以发现颤振临界风速并不随结构阻尼比成线性增长而是增长率不断降低的趋势.此外,如图14所示,当结构阻尼比较低时(ζ=0.05%、0.1%、0.15%),仍具有明显的颤振拍现象,由此可见低阻尼情况下同样存在颤振拍现象.颤振拍现象随结构阻尼比的增长而不断弱化,如图15和16所示,当结构阻尼比为0.5%时颤振拍现象很快消失并达到单频稳幅的振动状态.另外,可以预见,随着跨度的增长,主梁的密频和低阻尼特性将越明显,因此越易产生间歇性颤振现象,这对主梁的颤振稳定性是有利的.这些在颤振频率附近的模态间歇性参与颤振能不断消耗断面从气流中吸收的能量,其作用相当于一个间歇性调谐质量阻尼器(TMD).该TMD的阻尼效果随着结构阻尼的增长而不断减小,因此可以预测其为颤振临界风速增长率随结构阻尼比增长而降低的一个重要原因,其具体效应有待进一步验证,因为颤振临界风速随结构阻尼的这种变化趋势还与气动阻尼随风速的非线性变化有关.
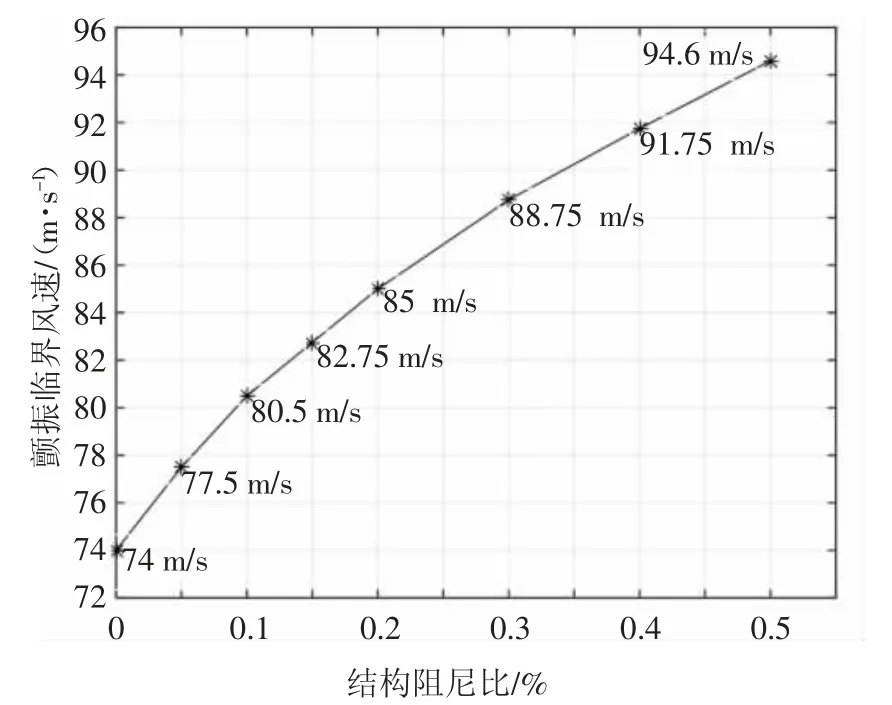
图13 模型FM-C不同结构阻尼比下的颤振临界风速Fig.13 The critical flutter velocity of model FM-C with different structural damping
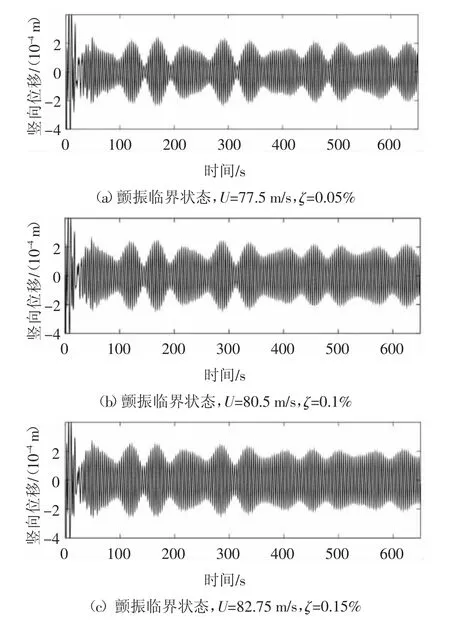
图14 不同结构阻尼比下FM-C颤振临界状态跨中竖向位移时程Fig.14 Vertical displacement response of FM-C at mid-span with different structural damping(Critical state)
接下来详细探讨结构阻尼比为0.5%时,中央扣对颤振临界风速以及主梁三维颤振形态的影响.图15和图16分别为风速94.6 m/s时FM-C跨中节点竖向位移和扭转位移时程,易知94.6 m/s为颤振临界风速,此值与风洞试验结果95.1 m/s[19]接近,说明程序计算结果是可信的.
对图15后500 s的位移时程做频谱分析,结果如图17所示.竖向和扭转位移都只有一个卓越频率0.257 8 Hz,原因是正结构正阻尼下,频率密集区的固有模态的位移响应迅速衰减,或颤振频率很难牵连带动频率密集区的固有模态间歇性参与振动.表5为4种模型颤振临界风速与颤振频率的对比,可知3种不同中央扣对颤振临界风速和颤振频率几乎无影响.为探明其机理,基于主梁所有节点的位移时程提取出颤振临界时的主梁振动形态,如图18所示.可见竖向振动的位移最大值在1/4跨位置,而主梁一阶对称竖弯的最大值在跨中,二阶正对称竖弯的最大值在1/4跨,如图19所示.因此其颤振振型由一阶正对称竖弯、二阶正对称竖弯、一阶正对称扭转振型相互耦合而成,但中央扣对这3种模态的频率几乎没有影响,从而导致3种不同中央扣对颤振临界风速和颤振频率几乎没有影响.
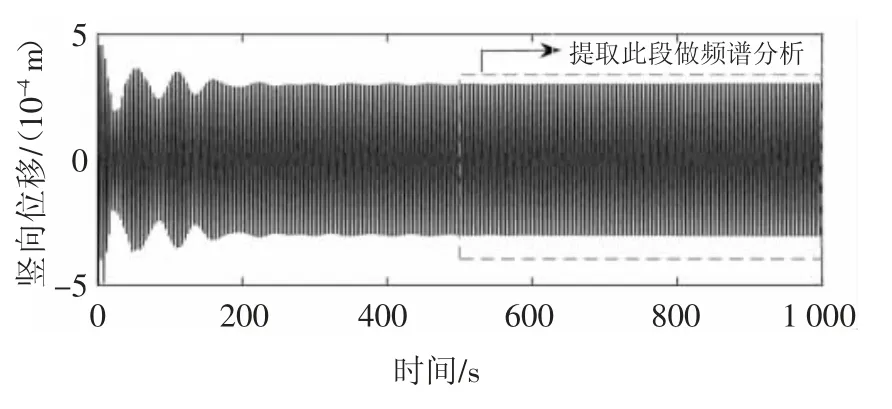
图15 FM-C跨中竖向位移时程(U=94.6 m/s,ζ=0.5%)Fig.15 Vertical displacement response of FM-C at mid-span(Critical,U=94.6 m/s,ζ=0.5%)

图16 FM-C跨中扭转位移时程(U=94.6 m/s,ζ=0.5%)Fig.16 Torsional displacement response of FM-C at mid-span(Critical,U=94.6 m/s,ζ=0.5%)
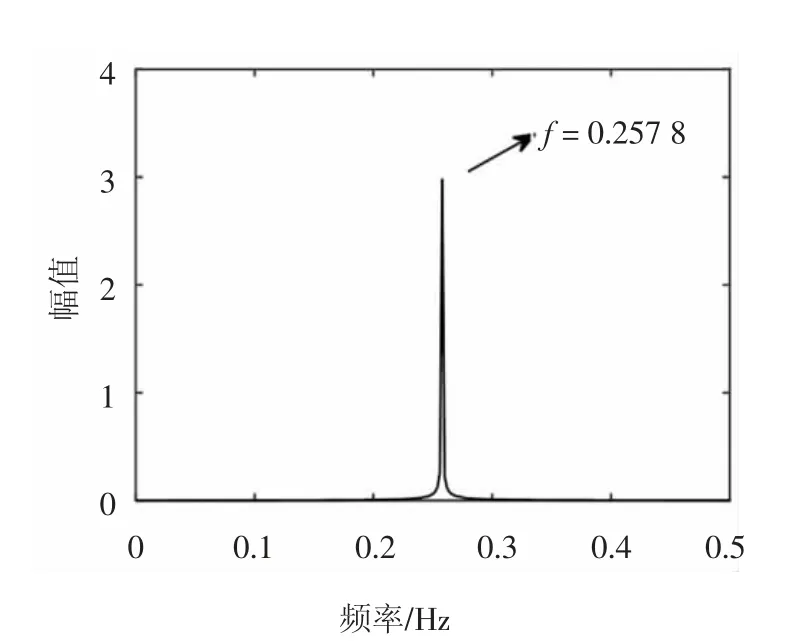
图17 FM-C跨中竖向位移响应频谱(U=94.6 m/s,ζ=0.5%)Fig.17 Spectrum of vertical displacement response at mid-span for FM-C(U=94.6 m/s,ζ=0.5%)
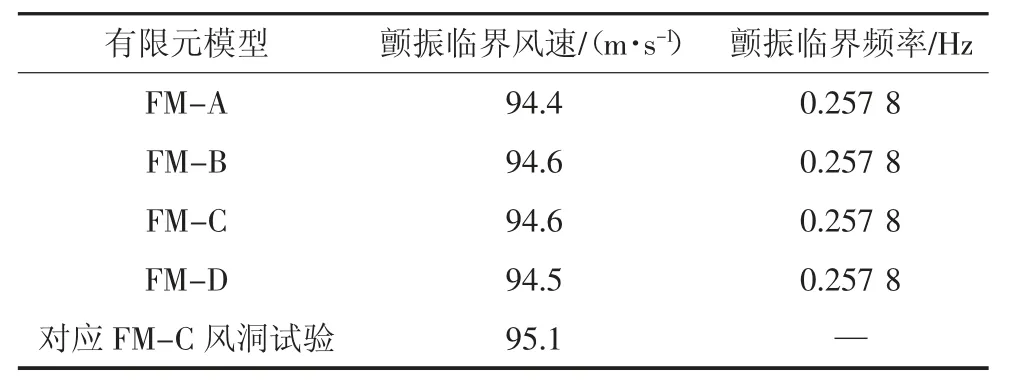
表5 4种结构形式中央扣颤振临界状态对比(结构阻尼比0.5%)Tab.5 Comparison of critical flutter state for four models(ζ=0.5%)

图18 4种模型弯扭耦合颤振振型(颤振临界状态,ζ=0.5%)Fig.18 The vertical-bending-torsion coupled mode shape of four models(Critical,ζ=0.5%)
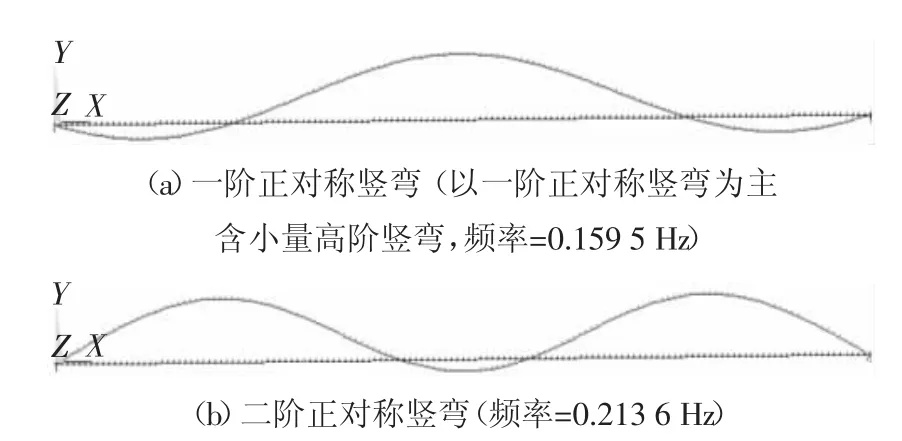
图19 模型FM-C的固有振型Fig.19 Natural mode shapes of the model FM-C
如图20和图21所示,当主梁发生弯扭耦合颤振时,其展向不同位置的位移响应存在相位差且同一位置处竖向位移与扭转位移也存在相位差.主梁不同位置之间的振动相位差即可定量揭示主梁振动时的展向同步性,同步性越高,能量越容易累积,颤振稳定性就越差,因此相位差的分析可以一定程度上揭示颤振稳定性的机理,同时可以通过4个模型的对比分析探究中央扣对主梁颤振展向同步性的影响.采用信号处理的方法可获得两个同频信号之间的相位差,图22为主梁其他位置与其跨中位置竖向位移相位差沿跨长的变化规律,可以发现模型FM-A的主梁其他位置与其跨中位置竖向位移相位差随着二者距离的增大而增大,最大达到25°.对比4个模型,可以发现关于跨中设置不对称的中央扣(非对称型的中央扣,如图4所示)打乱了局部位置处相位差随距离增大而增大的规律,并增大了主梁左边与跨中处的竖向位移相位差,最大达40°,中央扣的不同形式造成的影响差别极小.整体上非对称型的中央扣有打乱主梁竖向位移展向同步性的趋势,这对颤振稳定性是有利的.
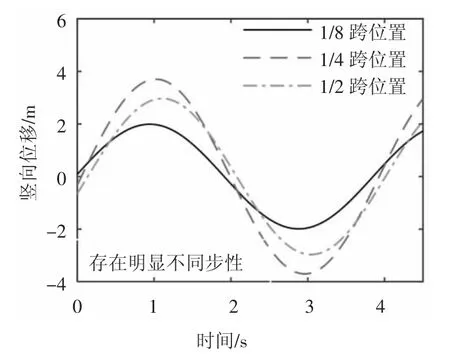
图20 FM-A主梁不同位置竖向位移时程Fig.20 Vertical displacement of main girder at different positions for FM-A
图23为主梁其他位置与其跨中位置扭转位移相位差沿跨长的变化规律,可以发现主梁其他位置与其跨中位置扭转位移相位差也随二者距离的增大而增大,但最大仅3°,说明主梁颤振时扭转位移展向同步性明显高于竖向位移.中央扣对主梁其他位置与其跨中位置扭转位移相位差的影响微弱.

图21 FM-A主梁1/4跨位置位移响应时程Fig.21 Displacement responses of main girder at 1/4 span position for FM-A

图22 颤振临界风速下主梁其他位置与跨中处竖向位移相位差(ζ=0.5%)Fig.22 Phase difference of vertical displacement response between mid-span and the other position of main girder(Critical flutter state,ζ=0.5%)

图23 颤振临界风速下主梁其他位置与跨中处扭转位移相位差(ζ=0.5%)Fig.23 Phase difference of torsional displacement response between mid-span and the other position of main girder(Critical flutter state,ζ=0.5%)
图24为主梁同一位置竖向位移与扭转位移之间的相位差沿跨长的变化规律,可知FM-A跨中位置竖向位移与扭转位移相位差最小,最小为14°,并向主梁展向两端不断增大.对比FM-A、FM-B、FM-C和FM-D,非对称型中央扣打乱了局部位置处竖向位移与扭转位移相位差由跨中向两边增大的趋势,增大了主梁左边竖向位移与扭转位移的相位差,最大达50°.由此可见,中央扣对主梁的整个三维颤振姿态产生比较复杂的影响.

图24 颤振临界风速下主梁竖向与扭转位移相位差(ζ=0.5%)Fig.24 Phase difference between vertical displacement and torsional displacement of main girder(Critical flutter state,ζ=0.5%)
3 结语
本文通过模态分析和颤振时域分析研究了中央扣的不同结构形式对大跨悬索桥自振频率及颤振稳定性的影响,得出以下结论:
1)3种不同结构形式的中央扣都能够大幅提高主梁纵飘的频率,其中刚性中央扣的增幅最大;对于侧弯和扭转振型,中央扣对反对称振型的影响要远大于正对称振型且刚性中央扣的影响最大,其中刚性中央扣能够提高15%一阶反对称扭转的频率;此外,竖弯振型的频率受中央扣的影响很小,主要由于中央扣仅提高了主梁跨中处的局部竖向刚度.
2)在不考虑结构阻尼情况下,3种不同结构形式的中央扣对颤振临界风速的影响都极小.此外,由于该桥的颤振频率落在固有频率分布密集的区域,因此,当不考虑结构阻尼或当结构阻尼比很低时颤振频率很容易牵连带动频率密集区的固有模态间歇性参与振动,出现间歇性颤振现象.
3)考虑结构阻尼时,3种不同中央扣对颤振临界风速与颤振频率的影响都极小,这是由于矮寨大桥以一阶正对称竖弯、二阶正对称竖弯和一阶正对称扭转相互耦合的振型发生弯扭耦合颤振,而中央扣对这些振型频率的影响甚微.刚性中央扣能提高15%一阶反对称扭转的频率,若主梁发生反对称竖弯和扭转耦合的颤振,可以预见中央扣将能大幅提高颤振临界风速甚至改变颤振振型.此外,通过主梁展向不同位置处颤振位移响应之间相位差的研究,可知主梁不同位置之间振动的同步性随着距离的增大而降低;该桥弯扭耦合振动时扭转位移的展向同步性要远高于竖向位移;中央扣对主梁的整个三维颤振姿态产生比较复杂的影响,一定程度上有利于颤振稳定性.
主梁颤振时不同形式的中央扣其局部位置的应力分布不同,当结构发生大幅振动时会对中央扣构件产生很大的疲劳损伤,尤其是刚性中央扣,因此下一步可进一步深入研究.

