城区内涝条件下城市公交-地铁双层交通网络的脆弱性分析

宋英华，李玉枝，霍非舟，梅依云

(1.武汉理工大学中国应急管理研究中心， 湖北 武汉 430070;2.安全预警与应急联动技术湖北省协同创新中心， 湖北 武汉 430070;3.武汉理工大学安全科学与应急管理学院，湖北 武汉 430070)

城市交通系统是城市基础设施系统的一个重要组成部分，随着经济的发展和城市人口的增加，人们对城市交通系统运营安全提出了更高的要求。近年来，长时间强降雨导致城市内涝现象频繁发生，城区内涝会造成交通站点或线路故障，影响公共交通系统的正常运行，甚至可能导致整个交通系统崩溃。公交、地铁为城市公共交通系统的主要组成部分，对其网络脆弱性进行分析有助于了解城市公共交通系统面对内涝灾害的脆弱性水平，明确城市交通系统网络中受影响最大的站点(连边)，并根据分析结果采取一定的控制措施，有益于保证城市内涝后交通网络的安全和有效运行。

由于城市交通系统是一个复杂的系统，因此国内外许多学者运用复杂网络理论来研究城市交通网络。如Sienkiewic等[1]对波兰22个城市公交网络的复杂网络特性进行了研究，证明了城市公交网络的小世界特性；Yang等[2]研究了北京地铁网络随机故障和蓄意攻击时地铁网络的鲁棒性；徐佩佩等[3]采用网络效率和相对连通度两个评价指标评价了城市公交网络拓扑静态结构的可靠性；薛锋等[4]识别并观察了成都地铁网络关键节点被蓄意攻击、普通节点被随机攻击后的网络性能变化趋势；吴贤国等[5]、甘俊杰等[6]分析了随机和蓄意攻击下武汉市地铁网络的脆弱性。

以上研究均是致力于对单一交通网络的研究，由于城市交通网络包含多种网络，国内外已有学者开始对城市双层交通网络进行研究，如罗艺等[7]构建了城市公交-地铁双层交通网络，但忽略了站点的差异性，将两种站点视为性质相同的节点；沈犁等[8]、Ma等[9]构建了城市双层交通网络模型级联失效模型，给出了定量化的耦合方式，但也未界定两种站点的差异性；张琳等[10]将空间信息嵌入到城市公交-地铁双层交通网络的研究中，考虑了站点的差异性且给出了具体的耦合方式，但是并未考虑站点及线路的重要度对于网络脆弱性的影响。此外，现有的交通网络研究大都是对于突发事件的研究，并没有对具体现象的研究。鉴于此，本文考虑构建公交、地铁无向加权网络和不同耦合半径的公交-地铁双层交通网络，确定连边的权重和节点的重要度，对武汉中心城区的公共交通网络系统进行综合分析，计算静态下地铁网络、公交网络和不同耦合半径的公交-地铁双层交通网络的网络特性指标，并以最大联通子图比例、网络连通率、网络效率为指标对城市内涝导致的失效现象进行故障模拟，分析地铁网络、公交网络和公交-地铁双层交通网络遭遇城区内涝后网络的脆弱性，这将有利于提高公交与地铁之间的配合效率和城市公共交通系统的安全性。

1 城市公交-地铁双层交通网络模型构建

1. 1 模型基本假设

考虑到城市公交、地铁网络的特性，本文做出如下假设：

(1) 暴雨引发的内涝造成的站点或道路损坏对双向交通的影响相同，因此构建交通网络时不考虑公交和地铁的方向性，构建无向网络。

(2) 不考虑站点位置,将距离较近且公交站点名称相同的站点视为同一站点,忽略具体停靠地点、站点间距离、站点大小对网络的影响。

(3) 站点间有多条边相连时将其视为一条边相连，不考虑公交和地铁发车间隔时间的影响，考虑连边的权重，构建加权网络。

1. 2 城市公交-地铁双层交通网络模型构建

本文提取实际的站点为节点、实际的线路为连边来构建公交网络、地铁网络，结合实际有直达线路才有边的特点，采用Space L方法来构建城市公交-地铁双层交通网络，并引入客流量为地铁网络的权重、客流量和两站点间经过的公交线路数为公交网络的权重，以保证构建的网络与实际的线网更加接近，在研究城市内涝灾害对公共交通网络的影响时也更加准确。

构建城市公交-地铁双层交通网络模型的步骤如下：

(1) 构建原始网络：对选取范围中的公交、地铁站点及其线路进行提取，对提取的站点及连边进行编号，定义Nb表示公交网络、Ns表示地铁网络，其中Vb、Vs为站点的集合，Lb、Ls为线路的集合。公交、地铁连边的权重wb、ws计算公式如下：

(1)

(2)

式中：Lij为站点i、j之间的客流量；Lbt、Lst为公交、地铁总客流量；Mij为站点i、j之间的公交线路数；Mt为总公交线路数，α+β=1。

(2) 建立公交-地铁站点对应关系：将公交网络、地铁网络映射到公交-地铁双层交通网络中，构成包含Nb和Ns〈Vs,Ls〉的双层交通网络，对双层交通网络中的站点进行重新编号，形成双层交通网络Nf。

(3) 构建耦合站点：以地铁站点为圆心创建耦合半径为R的耦合区(耦合半径R可取250 m、500 m、750 m)，利用ArcGIS软件识别出耦合区内的公交站点，地铁站点与耦合区内的公交站点构成耦合关系。

(4) 构建双层交通网络的新连边：对具有耦合关系的公交站点、地铁站点建立新的连边，如图1所示的f1和f5之间的连边，构成新的双层交通网络Nf。

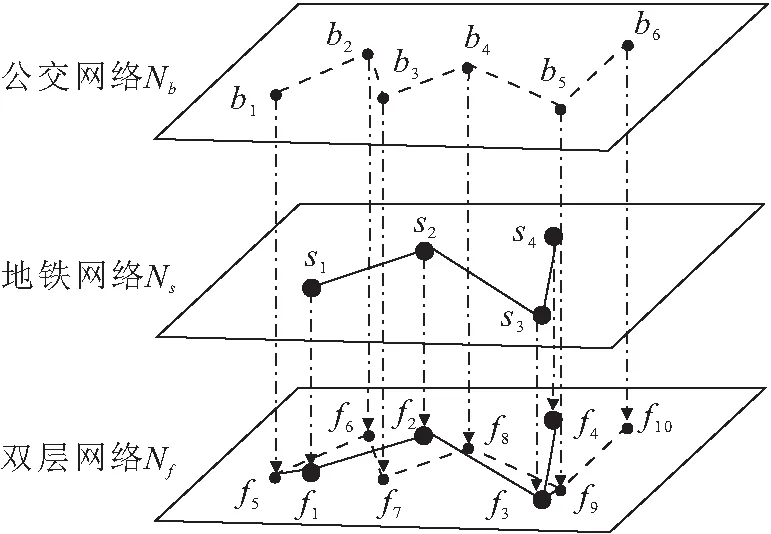
图1 城市公交-地铁双层交通网络模型Fig.1 Urban two-layer traffic network model of bus and subway

2 城市公交-地铁双层交通网络脆弱性分析

2. 1 网络结构脆弱性指标

利用复杂网络理论计算网络脆弱性的常用指标有平均度〈k〉、介数B、最大连通子图比例S和网络效率E，其计算公式[4]如下：

(3)

(4)

(5)

(6)

(7)

上式中：n为节点数;k为与节点i相邻的边的数量;njl为节点j、l之间最短路径数量；njl(i)为节点j、l之间经过i节点的最短路径数量；μn(i)为以节点i为起点经n个连边回节点i的回路数目;S0为初始最大联通子图数;dij为节点i、j之间的距离。

动态网络分析一般选择网络效率E来衡量网络运输效率，选择最大联通子图比例S从信息传递方面来衡量网络的联通性能，基于此本文增加网络连通率δ,从拓扑结构方面来衡量网络的连通性能，其计算公式如下：

(8)

式中:P表示删除节点后的网络；nij为连通系数，若节点i和j之间连通，则nij=1，否则，nij=0。

2. 2 网络重要度指标

关键节点的识别对于网络脆弱性分析很重要，传统方法通常采用单一的节点度或节点介数作为重要度指标，由于节点度和节点介数在重要度上各有侧重，且客流量等实际变量也对节点的重要性有影响，因此本文定义重要度指标wi如下：

(9)

式中：ki、Bi、Li分别为节点i的度、介数、客流量；kt、Bt、Lt分别为所有点的总度数、总介数和总客流量。

2. 3 网络攻击策略

暴雨导致的内涝主要影响城市道路的正常通行，内涝的严重程度不同，其影响范围也不同，本文忽略有积水但仍能通行的状态，仅考虑单个站点或道路无法通行及更严重的状态，针对不同的严重程度对网络进行不同类型的攻击，对于单个站点无法通行的状态进行单节点蓄意攻击，对于部分站点或部分道路无法通行的状态，考虑一般情况和最坏情况分别进行累计节点随机攻击和蓄意攻击。

(1) 单个节点蓄意攻击：对网络中的单个节点进行蓄意攻击，针对重要度大小顺序对于网络中节点依次攻击，每次攻击结果对后续攻击不产生影响。

(2) 累计节点攻击：累计节点攻击流程见图2。

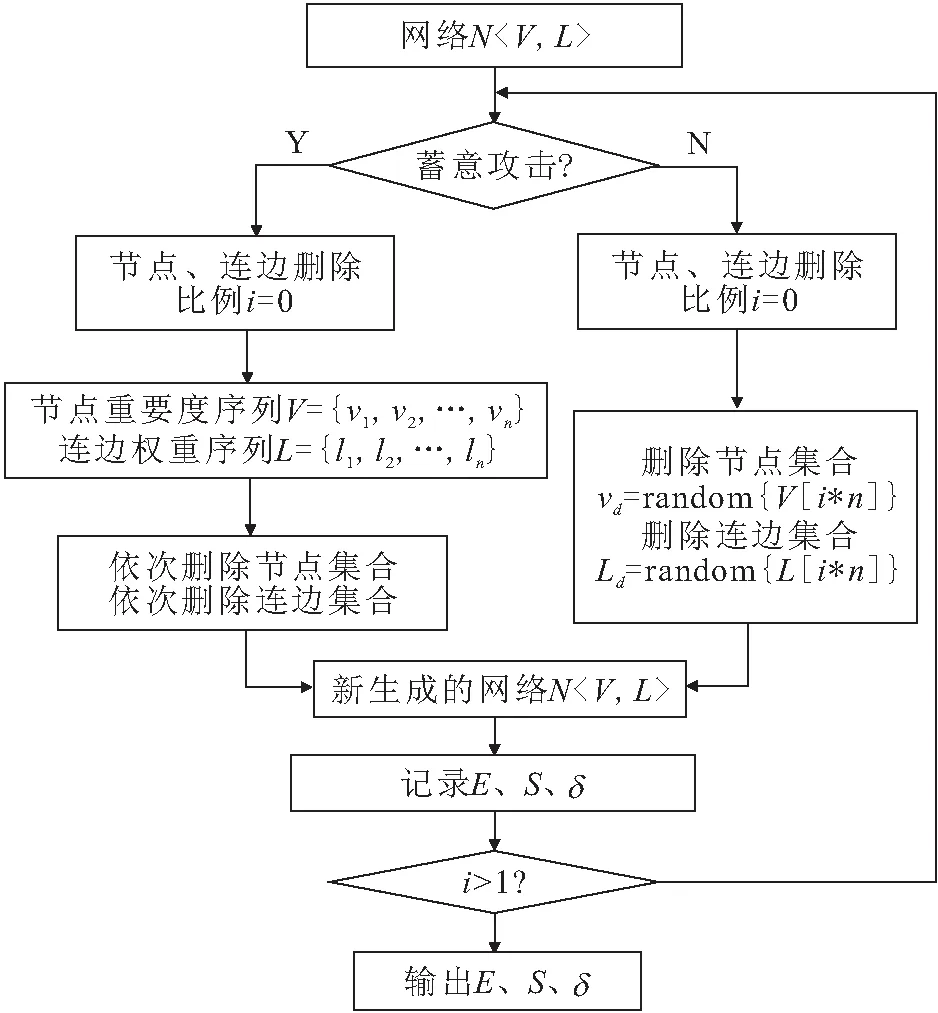
图2 累计节点攻击流程图Fig.2 Flow chart of cumulative node attack

3 实例应用与分析

3. 1 构建武汉中心城区公交-地铁双层交通网络

根据实时更新的地图所提供的武汉市二环内公交网络、地铁网络的数据，武汉市二环线内有69个地铁站点和370个公交站点(包含常规公交站和BRT公交站)，对站点及线路进行编号并构建单一的公交网络、地铁网络；利用ArcGIS软件识别出二环线内的公交站点、地铁站点，并利用软件根据给定的耦合半径识别出具有耦合关系的公交站点与地铁站点，构建武汉市公交-地铁双层交通网络(以下简称双层网络)，见图3。

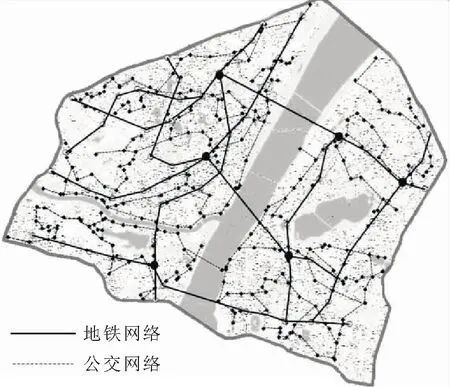
图3 武汉市公交-地铁双层交通网络图Fig.3 Map of bus and subway two-layer traffic network

3. 2 静态网络结构脆弱性分析

根据上述构建的武汉市二环内的公交-地铁双层交通网络的拓扑结构图，通过Pajek软件和MATLAB编程计算地铁网络、公交网络和双层网络的网络特性，其计算结果见表1。

表1 地铁网络、公交网络和双层网络的网络特性指标计算结果

由表1可知，地铁网络、公交网络和双层网络的最大联通子图比例都是1，说明三类网络都具有较完整的网络结构；地铁网络、公交网络和双层网络都具有较大的平均路径长度和极小的聚类系数，且网络效率较低，表明站点之间可能存在联系不够紧密、网络拓扑结构不够完善等问题。

选取耦合半径R为500 m的双层网络，对地铁网络、公交网络和双层网络的站点度分布情况进行分析，其结果见图4。

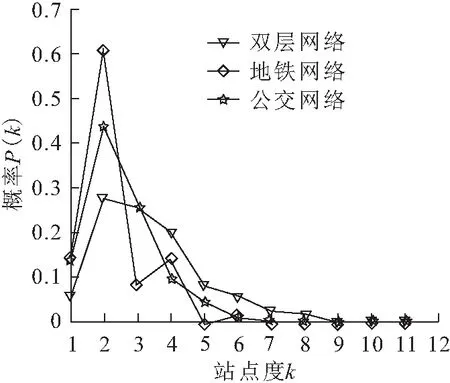
图4 地铁网络、公交网络和双层网络的站点度分布图Fig.4 Distribution map of site degree of subway network, bus network and two-layer traffic network

由图4可见，公交网络、地铁网络站点度最大值都为7，远小于双层网络站点度最大值11，且双层网络站点度值集中在2～5之间，其站点度值为4～6的站点数量相比公交网络、地铁网络大幅增加。由此可见，双层网络站点的平均连通程度和局部承载性能均优于单一交通网络。

3. 3 动态网络结构脆弱性分析

城市内涝会造成站点无法正常运行，或者是使道路无法正常通行，甚至可能会影响其他站点或者使整条线路无法正常运行，即内涝会造成城市公共交通网络中部分节点或连边的失效，破坏城市公共交通网络的完整性。对武汉市二环内的地铁网络、公交网络和双层网络进行内涝状态下的故障模拟，每次攻击2%的节点或连边，利用MATLAB软件进行计算，以最大连通子图比例的相对大小S、网络连通率δ来反映交通网络的连通性能，以网络效率E来反映交通网络的运行效率。

3.3.1 单个节点蓄意攻击

由于单个节点蓄意攻击时大部分节点对于网络效率的影响较小，因此本文仅对重要度排序前70的站点进行计算，其计算结果见图5。

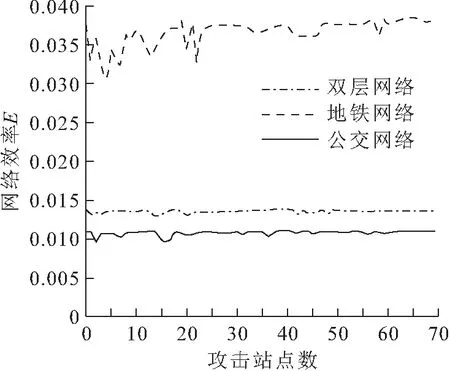
图5 单个节点蓄意攻击下网络效率的变化情况Fig.5 Change of network efficiency of single node attack

由图5计算结果可知，地铁网络中影响最大的站点为江汉路，其失效后整个地铁网络的网络效率下降20%，其次对地铁网络影响较大的站点依次为三阳路、螃蟹岬、积玉桥、大智路、香港路，对地铁网络网络效率的影响均大于10%；双层网络中影响最大的站点为螃蟹岬，其失效后整个双层网络的网络效率下降7.2%，其次对双层网络影响较大的站点依次为武昌火车站公交站、鹦鹉大道地铁琴台站、三阳路、积玉桥，对双层网络网络效率的影响均大于5%；公交网络中影响最大的站点是武昌路阅马场，其失效后整个公交网络的网络效率下降4.5%，其次对公交网络影响较大的站点为中山大道硚口、武胜路江汉桥，对公交网络网络效率的影响仅为3.6%，说明公交网络中的单个站点对网络效率的影响较小。

3.3.2 累计节点随机攻击

随机攻击模拟一般情况下是模拟城市内涝导致的交通影响，内涝会导致节点故障和连边故障两种状态，故针对这两种状态下地铁网络、公交网络和双层网络的动态脆弱性指标进行分析。由于随机攻击下3种不同耦合半径的网络脆弱性指标的速度变化率相似，因此仅选择耦合半径R为500 m的双层网络进行随机攻击。随机攻击一次的结果具有随机性，因此进行三次计算并对网络脆弱性指标取平均值，其计算结果见图6至图8。

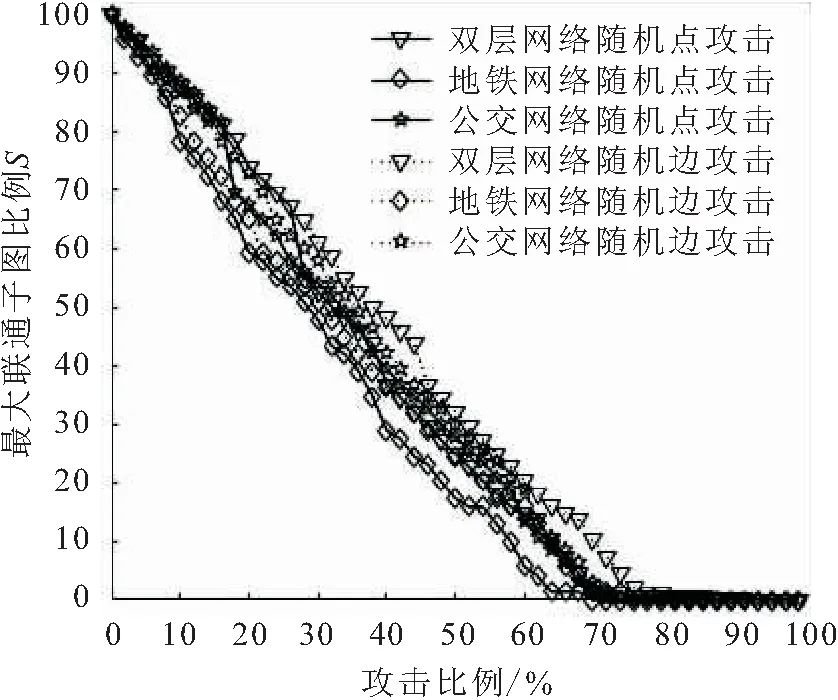
图6 累计节点随机攻击下网络最大联通子图比例S的 变化情况Fig.6 Change of the maximum connection subgraph ratio of network S of cumulative node random attack

由图6可见，随机点攻击S值的下降幅度小于随机边攻击，说明随机点攻击更容易影响网络的连通性；相较于公交网络、地铁网络，双层网络S值的下降速率更慢，受到攻击后保持着较好的联通性能；单一的地铁网络S值下降速率更快，受到攻击后网络脆弱性更大，随机攻击比例为20%的地铁站点就能使地铁网络的S值降低40%。三类网络随机攻击时都存在S值骤减情况，这可能是由于删除了重要节点、连边的原因。

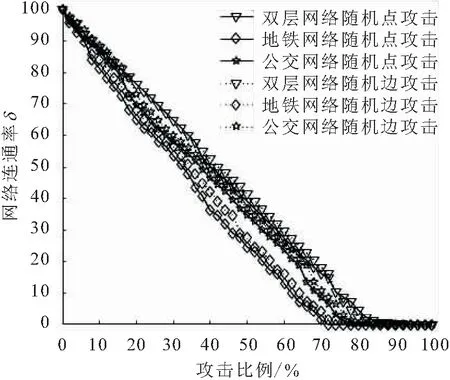
图7 累计节点随机攻击下网络连通率的变化情况Fig.7 Change of network connectivity of cumulative node random attack

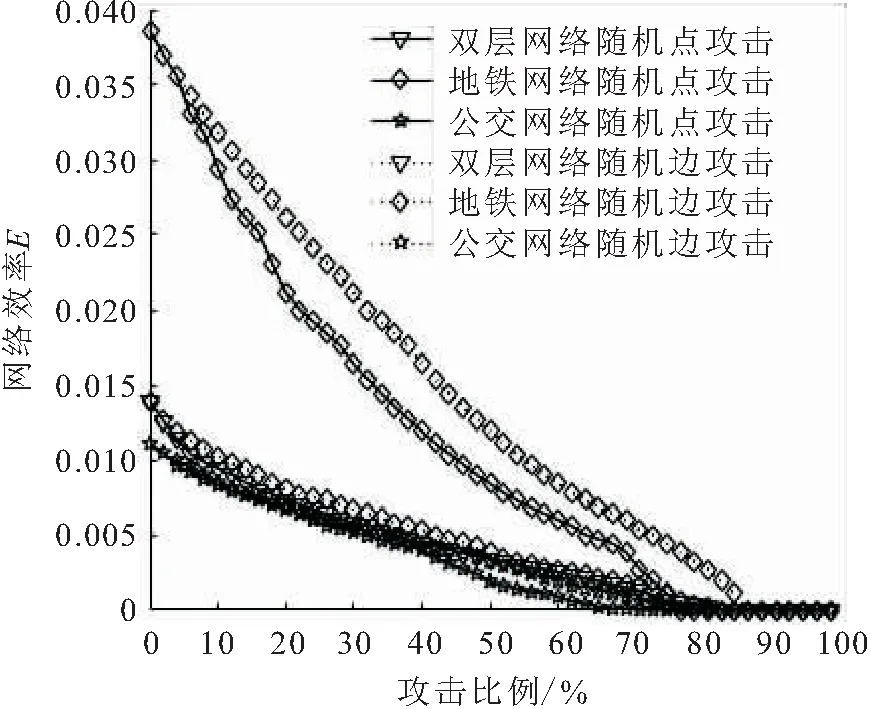
图8 累计节点随机攻击下网络效率E的变化情况Fig.8 Change of network efficiency E of cumulative node random attack

由图7可见，三类网络的δ值下降速率较为平稳，随机攻击比例为10%的节点和连边时三类网络的δ值变化情况一致，攻击更多的节点和连边时，地铁网络的δ值大小始终处于三类网络中的最低值，双层网络的δ值最高；从δ值变化来看，随机攻击比例为72%的地铁站点、78%的公交站点、82%的双层站点时，网络彻底崩溃，说明节点攻击对网络连通性能的破坏更强，因此在评估交通网络脆弱性时应优先进行节点脆弱性分析。

由图8可见，地铁网络的E值远大于双层网络和公交网络，且其E值的变化率也远大于其他两类网络，节点攻击使E值衰减得更快，这表明对重要的站点进行保护后，网络会具有一定的抗毁性；地铁网络攻击比例为22%的节点和连边时E值下降速率较快，攻击比例为22%～65%的节点和连边时E值下降速率相对缓慢，攻击比例为65%以上的节点、连边时E值下降速率较快。

3.3.3 累计节点蓄意攻击

模拟节点、连边蓄意攻击得出的网络脆弱性指标变化情况相似，本文选取节点重要度指标进行蓄意攻击下的结果分析，分析公交网络、地铁网络和三种耦合半径的双层网络受到蓄意攻击后的脆弱性指标变化情况，其计算结果见图9至图11。

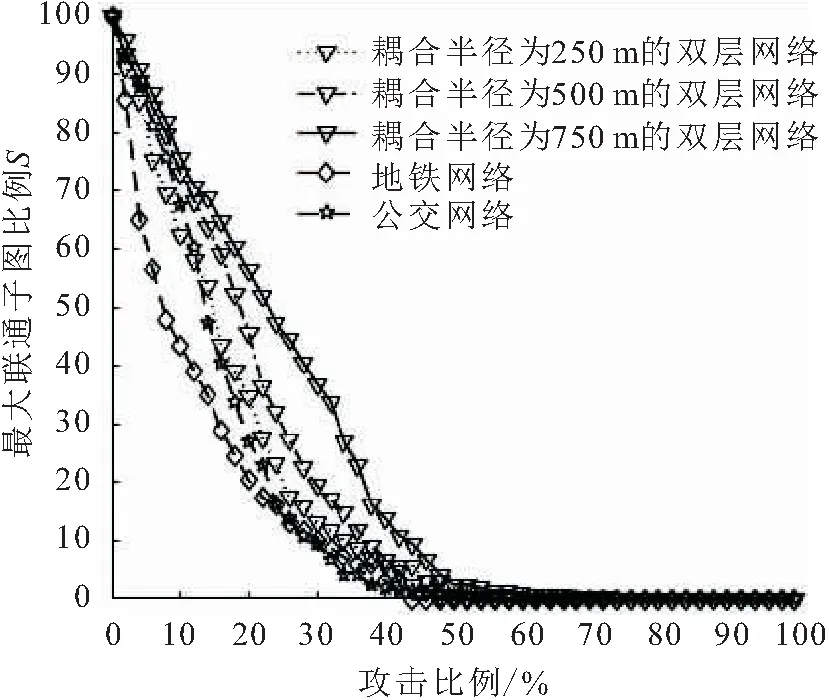
图9 累计节点蓄意攻击下网络最大联通子图比例S的 变化情况Fig.9 Change of the maximum connection subgraph ratio of network S of cumulative node intentional attack

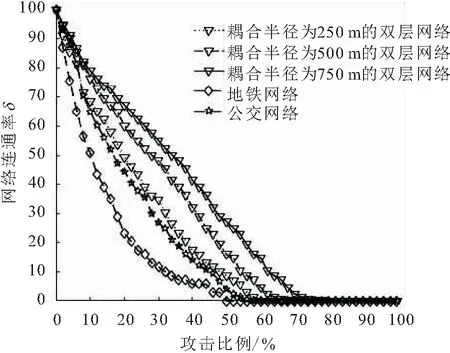
图10 累计节点蓄意攻击下网络连通率δ的变化情况Fig.10 Change of network connectivity δ of cumulative node intentional attack

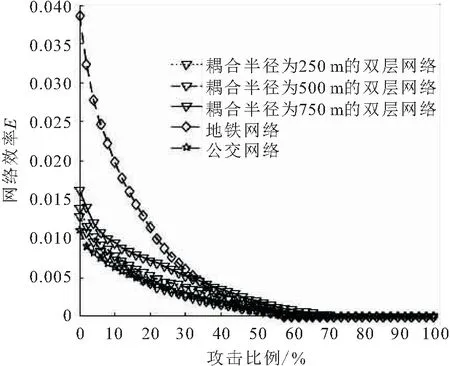
图11 累计节点蓄意攻击下网络效率E的变化情况Fig.11 Change of network efficiency E of cumulative node intentional attack

由图9和图10可见，随着耦合半径的减小，双层网络连通性更易受影响，网络脆弱性逐渐增大；地铁网络的S值下降速率最快，蓄意攻击比例为10%的地铁站点就能使S值降低56.5%，这是由于地铁网络相较于公交网络结构更简单、站点少、无聚类性，受到蓄意攻击时网络脆弱性较大；攻击比例为14%的节点时耦合半径为250 m的双层网络比公交网络S值下降速率快，这是由于部分重要地铁站点被攻击的原因；从δ值变化来看，随机攻击比例为50%的地铁站点、56%的公交站点时会使网络彻底崩溃，而双层网络需要攻击更高比例的站点才会使网络彻底崩溃。

由图11可见，耦合半径越大的双层网络初始E值越高，E值的下降速率越慢，网络的脆弱性越小；公交网络和双层网络攻击前10%的节点时E值的下降速率较快，地铁网络攻击前40%的节点时E值下降速率较快，因此应对江汉路、三阳路、螃蟹岬、积玉桥、大智路、香港路这些对网络效率影响较大的地铁站点制定相应的应急预案与保护措施。

4 结论与建议

(1) 本文结合实际构建了地铁、公交无向加权双层交通网络模型，设定了连边权重和节点重要度的定量指标，以武汉市中心城区为例对内涝状态下的交通网络进行了分析，结果表明：地铁网络、公交网络和公交-地铁双层交通网络在蓄意攻击下表现出一定的网络脆弱性，节点故障对网络脆弱性的影响更大。对于城市的管理与规划者来说，应重视重要度大的节点、权重高的连边。

(2) 通过对单一交通网络和双层交通网络的对比分析，发现双层交通网络整体抗毁性能强于单一交通网络，且耦合半径越大，双层交通网络的抗毁性能越好。基于耦合半径的耦合站点定量化识别，有利于强化公交与地铁站点间的连通性和提高站点周围公共自行车覆盖率。

(3) 本文仅考虑了内涝严重造成站点或路段障碍的情况对于城市交通的影响，但未对内涝造成的少量积水对城市交通的影响进行研究，这将是今后的研究方向。