高速公路气象数据融合滤波与短时雨雾预测

贾 骏，朱 旭，闫茂德，林 海

(长安大学 电子与控制工程学院，西安 710064)

0 引言

雨雾天气下能见度低，可视距离较短，严重影响高速公路行车安全，易引发交通事故[1-3]。2019年10月3日，宁洛高速因雨雾天气发生4起交通事故，共造成10人死亡，7人受伤；2019年12月6日，贵州蓉遵高速收费站附近因浓雾导致连环追尾事故。若能提前获知行驶路段的雨雾天气状况，将极大提高高速公路雨雾天气下的行车安全性[4-5]。

近年来，很多学者在雨雾等恶劣气象预测方面进行了诸多研究，并提出一系列预测方法。沈艺高[6]使用改进粒子群BP神经网络算法成功预测雨天发生的概率。宫宇[7]等通过对比研究验证了GRAPES-GFS模式对短时效内降水预测的有效性。夏凡[8]等通过对比试验提出一种有效的雾天气预报方法。艾洪福[9]使用多元线性回归法分析空气中PM2.5含量实现了雾天气的预测。程美英[10]等利用SVM算法分析主要影响因子对雾天气进行预测。沈行良[11]等利用雾监测器和GPRS技术对雾气实时监测，并将雾气监测结果上报到用户手机。上述气象预测中，通常使用单一类型的数据进行分析预测，未能考虑各类气象数据之间的相互关系，对数据中的信息利用不够充分。

在数据相关关系研究方面，已有学者进行了一些研究。曾强[12]等采用时空交互模型对季节事故数和道路设计参数、气象特征之间的内在联系进行分析，明确了各因素之间的内在联系。胡立伟[13]通过建立N-K模型和改进的耦合度模型对地质、气象环境与公路交通风险之间的关系进行分析。张彬[14]等利用相对位姿数据和绝对位姿数据之间的关系，采用卡尔曼滤波实现了数据融合。这些方法通过分析数据之间的相关关系对数据进行融合，提高数据利用率。

然而，上述天气预测和数据相关性研究大都在各自领域进行探索，未能将两者的优势相结合，利用数据之间的相关数值进行数据融合，并将结果用于气象状态预测，有助于提高数据利用率和气象状态预测精度。为此，本文通过联合概率法计算各传感器数据与气象数据类型之间关联概率，设计特征值提取函数形成多源异构数据融合模型。然后，将数据融合模型与卡尔曼滤波相结合，构建异构数据协同融合滤波模型，对异构气象数据融合的同时降低噪声干扰，提高后续预测精度。最后根据融合滤波数据利用贝叶斯最大熵方法进行短时雨雾预测。

1 异构气象数据融合滤波模型

高速公路路域内气象数据(温度、湿度、能见度等)使用多类传感器采集，导致获取的气象数据具有异构性，增加了数据融合的难度。为了充分利用异构数据之间的内在关系，同时降低数据中噪声影响，实现异构气象数据融合，设计异构气象数据融合滤波方法，如图1所示。

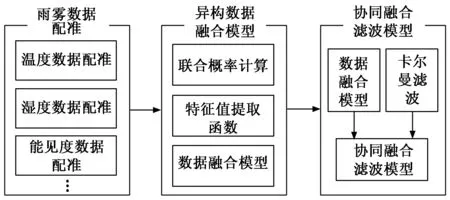
图1 异构气象数据融合滤波框架

首先，对温度、湿度、能见度等雨雾数据进行配准，得到统一时间表示的数据，便于后续异构数据融合；接着，利用联合概率法求取配准数据与气象数据类型之间关联概率，设计特征值提取函数，构建异构数据融合模型，对气象数据进行融合。最后，将数据融合模型与卡尔曼滤波相结合，构建协同融合滤波模型，实现对雨雾数据融合同时降低数据中噪声影响，为后续雨雾预测提供精准雨雾信息。

(1)

式中,

(2)

式中，xT∈I1=(xl1,xh1),xl1,xh1为温度区间下限和上限，xH∈I2=(xl2,xh2),xl2,xh2为湿度区间的下限和上限，xV∈I3=(xl3,xh3)，xl3,xh3为能见度区间的下限和上限。

1.1 数据配准

使用温度、湿度和能见度等传感器进行气象数据采集时，由于不同传感器采样时刻、采样周期等的差异，导致气象数据采样时间不同步，难以在同一时间尺度上对数据进行有效融合。为此，采用拉格朗日三次插值法对气象数据进行时间配准，利用配准时间点最近的3个采样值进行插值计算，得到一系列特定时间点上的温度、湿度和能见度等气象配准数据，为后续数据融合提供数据支持，配准公式如下：

(3)

经过上述时间配准处理，得到一系列相同时间节点的数据，便于后续数据融合，提高异构气象数据融合结果的准确性。

1.2 异构数据融合

为了充分利用异构气象数据中的信息，对配准后的异构数据进行融合，融合的关键是获取异构气象数据之间的相关关系。为此设计如下异构气象数据融合方式。

首先采用联合概率法求取各传感器数据与各气象数据类型之间的关联概率。将tk时刻各传感器数据与气象数据类型之间可能出现的组合关系θ(tk)表示为：

(4)

式中，θij,l(tk)为tk时刻第l个组合中与气象类型j相关联的第i个传感器的配准数据，i=1,2,…,m为tk时刻第i个传感器的配准数据，j表示第j类气象数据，l=1,…,m×n为第l个组合。

然后，通过贝叶斯法则计算tk时刻各传感器配准值与气象数据类型之间的关联概率：

αij(tk)=p(θij,l(tk)|Ztk)

(5)

式中，αij(tk)为tk时刻第i个传感器配准数据与第j类气象数据之间的关联概率，Ztk={Z(t1),Z(t2),…,Z(tk)}表示直到tk时刻得到的气象数据集合，其中：

(6)

(7)

通过联合概率方法，得到传感器数据与气象数据类型之间的联合概率，利用该联合概率设计气象数据的特征值提取函数，形成多源异构气象数据融合模型，对异构气象数据进行融合，具体的融合模型表述为：

(8)

式中，αij(tk)为tk时刻第i个传感器对于第j类气象数据的特征值提取函数。

上述方法，根据配准后的气象数据与各类气象数据之间的联合概率设计特征值提取函数，并构建异构气象数据融合模型。其中，数据配准保证融合数据具有统一的采样时间，便于进行数据融合，结果更准确。根据联合概率设计的特征值提取函数，形成的气象数据融合模型能够充分利用气象数据之间相关关系，融合结果能够精确描述所有的雨雾信息，有利于提高后续雨雾预测精度。

1.3 协同融合滤波

在实现气象数据融合的基础上，为降低噪声带来的影响，提高雨雾预测的精度。将数据融合模型与卡尔曼滤波方法相结合，构建面向多源异构数据的协同融合滤波模型，对数据进行融合滤波处理，对气象数据融合的同时抑制噪声，协同融合滤波模型为：

(9)

(10)

式中，Q,R为协方差矩阵，δab为克罗内克函数：

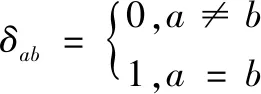
在构建异构气象数据融合滤波模型基础上，使用卡尔曼更新方程对所有采样数据进行融合滤波处理：

状态估计一步预测：

(11)

状态方程的雅克比矩阵：

(12)

一步预测误差协方差矩阵为：

(13)

增益为：

K(tk+1)=p(tk+1|tk)HT(tk+1)(H(tk+1)p(tk+1|tk)·

HT(tk+1)+R(tk+1))-1

(14)

协方差更新为：

p(tk+1|tk+1)=(In-K(tk+1)H(tk+1))p(tk+1|tk)

(15)

经过上述处理，利用各传感器配准数据与气象类型之间的联合概率，设计特征值提取函数并构建异构气象数据融合模型，对配准后的数据融合，得到较为准确的融合信息。然后将融合模型与卡尔曼滤波相结合，构建协同融合滤波模型，对异构气象数据进行融合的同时抑制噪声，得到统一表征雨雾信息的状态量，为后续雨雾预测提供准确的雨雾信息，提高预测精度。

2 基于贝叶斯最大熵的高速公路雨雾气象预测

在完成异构气象数据融合与滤波的基础上，设计短时雨雾预测方法，对目标路域内的雨雾天气进行预测。为此，采用贝叶斯最大熵方法[15-16]对高速公路路域内的短时雨雾天气进行预测，为驾驶员提供及时、准确的雨雾信息，增强高速公路交通安全。该预测方法主要分为先验阶段和后验阶段，其框架如图2所示。

图2 高速公路雨雾预测框架

先验阶段利用熵值越小事情发生概率越大的原理，用拉格朗日法求取约束条件下最大的先验概率密度，得到最小熵值，将最大的先验知识融入到先验概率密度中，提高雨雾预测精度。后验阶段用贝叶斯条件公式对先验知识、融合滤波得到气象数据和原始测量数据进行运算，得到后验概率密度，根据该概率密度对短时雨雾气象状态进行预测。

2.1 先验阶段

对现有的先验知识(气象常识、自然法则和专家知识等)进行表示，利用信息与熵之间熵值越小事情发生概率越高的内在联系，将抽象的先验雨雾气象信息转化为数学描述的信息。求取最大的概率密度保证熵值最小，将最大的先验知识融入到先验概率密度中，提高后续雨雾预测精度。

info(xmap)=-ln(fG(xmap))

(16)

式中，fG(xmap)为基于先验知识关于xmap的先验概率密度，计算数学期望：

(17)

为求取最大先验概率密度值，保证熵值最小，同时将最大的先验信息用于短时雨雾气象预测，使用方差约束条件，利用拉格朗日法求取最大的概率密度。约束方程下的概率密度为：

(18)

式中，λ为拉格朗日乘子，xd为xmap中的数据，N为数据集xmap中的数据个数。对上式求取最值，得到约束条件下最大的概率密度函数：

(19)

经过上述过程，使用最大熵原理，在约束条件下得到最大概率密度，将最大的先验知识融入到先验概率密度之中，得到最大程度贴近真实状况的先验概率密度fG(xmap)，为后验概率密度计算提供最大量的先验信息，提高雨雾预测的精度。

2.2 后验阶段

该阶段综合利用先验概率密度、融合滤波后的数据、原始测量的区间数据，使用贝叶斯原理对未来某一时空xk的后验概率密度fall(xk)进行计算。根据得到的后验概率密度值分析时空xk下的雨雾信息。贝叶斯条件计算公式[17]为：

(20)

式中，fall(xk)表示全体知识下的后验概率密度值。由于原始测量数据为区间类型数据，采用积分的形式对后验概率密度进行计算：

(21)

式中，I1,I2,I3分别为温度、湿度和能见度的积分区间。该公式实现了先验概率到后验概率的转化，同时对所有雨雾知识信息加以利用。

通过贝叶斯条件公式，综合利用先验概率密度、融合滤波后的和原始测量数据得到雨雾状态的后验雨雾概率密度信息，用于分析判断未来xk时空下的雨雾状态，概率密度值越高发生雨雾天气的可能性越高。

3 实验结果与分析

为验证提出的高速公路短时雨雾气象预测方法的可行性与准确性，利用陕西咸旬高速姜嫄河大桥路段的气象数据展开雨雾气象预测研究。该路段临近姜嫄河，空气湿度较高，雨雾天气频发。

基于2019年5月7日的雨雾气象数据，进行雨雾天气短时预测实验，在该路段每隔30 m设置一套温度、湿度和能见度检测装置，该装置温度、湿度最佳探测范围是25 m，能见度最佳工作范围25 km，预测未来两个小时的雨雾状态，连续预测22个小时。

为了验证预测结果的准确性，使用平均绝对误差值(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)两个指标对预测精度进行评价：

(22)

(23)

式中，n为样本点个数，yi,xi分别表示预测值和实际值。

MAE和RMSE是预测精度的一个量度，用于衡量预测值与实际值之间的接近程度。MAE和RMSE的值越小，表明该方法的预测精度越高。预测结果如图3～5所示。

图3 温度预测结果

由于本方法使用0点之后的雨雾数据开始预测未来两个小时的雨雾状态，因此预测结果从凌晨2点开始。通过预测结果图可知，凌晨3点到6点之间出现降水，且在5点之后降水开始减少，表现为图3温度在此期间持续下降、图4中空气湿度持续上升，并且3点到5点之间能见度保持较低水平，5点之后温度和湿度基本保持不变。8点到11点之间出现了雾，且没有发生降水，表现为在此期间能见度较低，但是温度略有提高和湿度变化较小。在11点到12点发生小强度降水，表现为图5中能见度较低，图4中湿度出现一个小幅增长，图3温度基本稳定。从下午3点到晚上8点，该地区发生小雨但雾气较小，表现为该时间段内温度持续下降和湿度上升。晚上8点之后有轻微降水发生，表现为温度、能见度回升，湿度有所升高。

图4 湿度预测结果

图5 能见度预测结果

通过对比看出本方法的预测值要比未使用最大熵方法，仅通过贝叶斯方法进行预测的结果精确，预测值更接近真实值，同时使用融合后的数据预测比直接使用测量数据预测的精度高，预测曲线离真实值曲线近。对比表明本文提出的高速公路短时雨雾预测精度更高，预测结果能反映真实雨雾天气状态。

通过对比图6先验概率密度函数和图7后验概率密度函数，后验概率密度曲线在0值处有更窄的残差和更高的概率分布值，表明使用后验概率密度进行雨雾判断更精确，预测精度更高。图7展示了预测得到的5月7号的雨雾发生概率，通过概率值判定的雨雾状态与实际雨雾状态相同，说明本方法预测的雨雾状态具有较高的可信度。

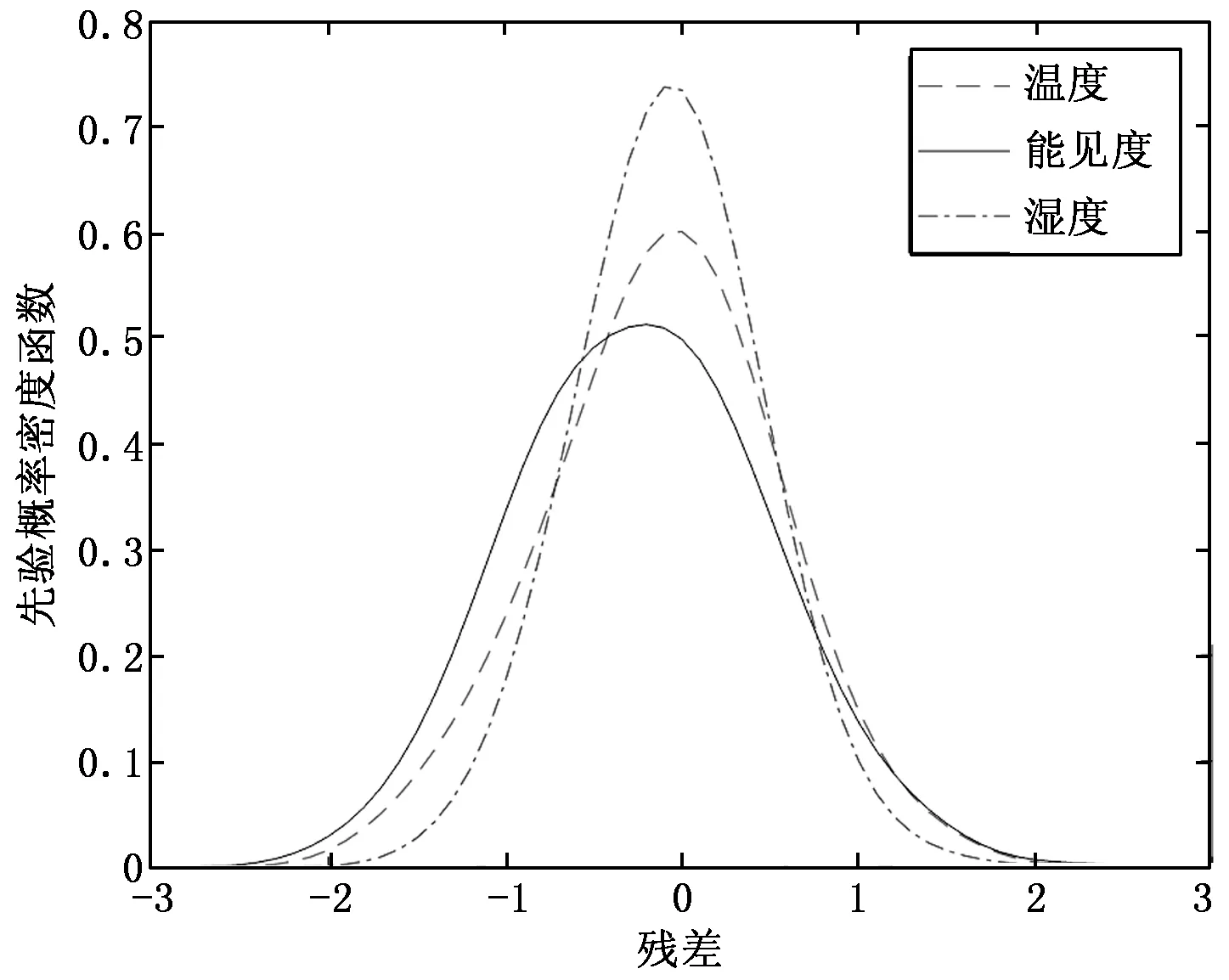
图6 先验概率密度函数

图7 后验概率密度函数

图8 预测结果

表1中分析了异构气象数据类型之间的相关关系，温度和湿度、能见度之间具有一定的负相关关系，湿度和能见度之间有一定的正相关关系。充分利用不同类型气象数据之间的相关关系，得到的融合结果更准确，有利于提高预测精度。表2中的降水和雾气预测的平均绝对误差和均方根误差的值相对较小，说明本方法对短时降水和雾气预测精度较高。

表1 数据类型相关性表

表2 预测精度表

综上可知，本文提出的根据异构气象数据融合滤波模型的结果，使用贝叶斯最大熵方法进行短时雨雾气象预测的方法，能够对高速公路短时雨雾状态进行有效预测，预测结果很好地反映真实的雨雾状态，可以为驾驶员提供及时、准确的雨雾气象信息，同时能够为交管部门实行车辆限速提供重要依据。

4 结束语

针对高速公路路域内短时雨雾气象预测难的问题，使用联合概率法获取各传感器配准数据与气象数据类型之间关联概率，设计特征值提取函数并建立多源异构数据融合模型。然后将数据融合模型与卡尔曼滤波方法相结合，构建异构气象数据协同融合滤波模型，对数据融合的同时降低数据中噪声影响，有利于提高预测精度。最后根据先验知识、融合滤波后的气象数据和原始测量数据，利用贝叶斯最大熵方法实现了高速公路短时雨雾预测。结果表明本方法能够实现高速公路短时雨雾状态的精准预测，为驾驶员提供及时、准确的雨雾气象信息，对提高公路交通安全、进行合理交通管制具有重要参考价值。