微处理器下的数字集成电路测试系统设计
郑 宇,方 岚,李苏苏,谢玉巧
(华东光电集成器件研究所,吉林 吉林 132001)
0 引言
数字集成电路芯片的设计、加工、系统整合方面的技术研究近来发展迅猛,但国内相关工作平台的设计与实现工作相对滞后。提供一个无需生产环境即可实现对数字集成电路进行相关测试的微处理器嵌入平台,是本文的研究重点。相关研究中,基于布尔差分法在微处理器的嵌入式控制下,对针对测试码集合对微处理器进行激励-反馈测试,是数字集成电路测试系统的主要实现模式。
代鹏(2020)等研究了一二次融合开关技术在数字集成电路测试系统中的应用及相关的电气细化设计[1]。王玉菡(2020)等研究了相变存储器单元在高速电流脉冲条件下的数字集成电路测试系统中的应用[2]。开关技术和寄存技术是高频信号发生的关键技术,在对高频数字集成电路的测试中,测试系统本身的高频性能必须超过待测试数字集成电路的高频信号需求且保留一定冗余。田强(2020)等研究了一种基于V58300平台的数字集成电路测试系统二次开发设计[3]。使用既有数字集成电路测试系统并通过二次开发过程使其潜在性能得到充分开发,也是当前数字集成电路测试平台开发的重要方向。石君(2020)等及王金萍(2020)分别对数字集成电路测试系统的相关算法[4]和测试方法[5]进行了研究。郑永丰(2019)等研究了在数字集成电路测试平台中融入射频信号发生功能的工程实现方法[6]。
基于上述技术文献的前期研究,本文基于TL5708-EVM-1000-64GE8GD-I开发板,设计一种可提供750MHz测试频率环境的数字集成电路测试系统。设计过程介绍如下。
1 数字集成电路的测试原理与可用技术分析
1.1 数字集成电路测试的任务模式
基于测试码构成的测试集,通过对数字集成电路的输入激励获取其输出响应,进而判断数字集成电路的不同故障模式。是当前数字集成电路测试系统的基本测试策略。详见图1。
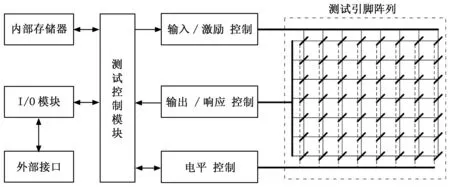
图1 集成电路测试系统的基本构成策略
图1中,存储器用来存储相关策略和测试集,I/O模块和外部接口用于连接外部控制设备,主要是桌面级工作站。以上模块及测试控制模块即核心开发板均属于通用模块,硬件开发压力较小。测试系统的核心硬件开发任务来自测试引脚阵列及其控制器模块的开发。详见图2。

图2 集成电路测试系统引脚设计图
图2中,使用一个非门电路对数据回路的输入输出进行晶闸管控制,形成一二次融合开关架构,从而进一步实现引脚的多用途复用。引脚的排列按照ICCC电气标准进行布局,可以实现对大部分标准封装数字集成电路的直接插入并进行引脚定义。
1.2 数字集成电路测试的布尔差分算法
对所有通过测试集可以测出的可测故障(Detectable Fault)编制测试集,且保持测试集的冗余度,分析所有可测故障的控制性,及所有测试集的相互包含和交集关系。最终构建测试集F(x)。
如果F(x)=F(x1,x2,…,xn)属于对所有变量有效的逻辑函数,那么其布尔差分定义函数为:
(1)

即数据响应错误可以向错误集传导,实现对所有可测故障的有效测量控制。
1.3 核心开发板的选型及引脚定义
本文选择TL5708-EVM-1000-64GE8GD-I开发板进行系统开发,该开发板提供8GByte的eMMC存储空间,提供1GByte的DDRIII高速动态存储器,ARM总线频率1 000 MHz,DSP总线频率750 MHz,除ARM A15核心处理器(CPU)外,还提供一个SGX544 3D+GC320的浮点处理器(GPU),具有较强的大数据分析处理能力。外部接口方面,支持GPMC拓展邬。可提供128 pix的DSP同步双工并行接入。
其中,为了满足一个32×32点阵的测试引脚阵列的DSP同步扫描,且支持至少32路输入输出控制,则应占用至少64 pix的I/O引脚进行扫描管理,至少占用16pix对引脚状态锁存器进行管理。同时,还应提供一个4×4键盘状态扫描模块,需要占用8 pix控制引脚,提供一个对MAX7219八位管控制器的控制功能,需要4 pix控制引脚。系统的扩展存储通讯在DATA总线上,外部通讯接口通讯在USB3.0总线上。
其引脚定义如表1。

表1 TL5708引脚定义表
表1中,冗余引脚共36 pix,占全部引脚的28.1%。其中主控信号引脚80 pix,占全部引脚的62.5%。
2 数字集成电路测试软件设计
2.1 软件基础算法
如图3,该数字基层电路测试系统的核心算法,来自其对测试集的顺序遍历和逐一判断,当发现基于布尔差分算法的正确响应时,直接跳转下一时钟循环,顺序遍历下一条测试集数据,而当发现基于布尔差分算法的错误响应时,根据其响应结果判断该可测故障的类型并计入到错误信息汇总表中。最终系统会将时钟循环过程中的错误状态进行一次判断,当不存在错误标志信息时,则直接显示PASS结果,而当存在错误标志信息时,则输出所有错误标志信息。

图3 基于布尔差分算法的数字集成电路软件设计流程图
在基础布尔差分算法的支持下,该软件实现方式可以实现对大部分可测故障的有效控制测量,但仍存在诸多不足:
首先,对不可测故障的测试存在短板。在单纯布尔差分算法下,存在可测故障(Detectable Fault)和不可测故障(Undetectable Fault)的差别,前者指可以通过固定的测试集反馈结果反映出被测试集成电路故障的测试结果,后者指无法通过固定的测试集反馈结果反映出被测试集成电路故障的测试结果。且电气工程视角下,芯片存在固定故障(Stuck Fault)桥接故障(Bridging Fault)时滞故障(Delay Fault)等,固定故障指某一位输出值保持电平不可控且不可变的电气问题,桥接故障指某二位或二位以上的输出值出现短路表现出电平的非逻辑性的同步变化问题,时滞故障指集成电路的高频响应能力低于预期使其在高频状态下不能做出正确响应的问题。这些故障很难在单纯使用布尔差分算法的前提下完成评价。
其次,无法对数字集成电路提出统观性的评价。传统测试条件下,较容易实现对出现可测故障的数字集成电路做出评价,但假定该集成电路处于无故障状态为状态0,而出现可测故障的状态为状态1,那么会有相当一部分集成电路模块处于介于0与1之间的故障状态。即该系统无法就不可测故障做出论断的前提下,较容易出现测试敏感度低,无法发现不稳定故障的系统设计问题。为判断出系统故障状态<1的统观性评价结果,需要在测试软件中引入机器学习模块以提供相应判断功能。
2.2 软件的机器学习功能实现
针对特定目标集成电路芯片的测试集,在单纯布尔差分算法支持下,会输出一组特定的判断结果。该结果一般包含3 000~6 000条记录不等。如果对这些记录进行统一输入到模糊神经元网络中进行判断,则模糊神经元网络的节点数量将空前增多,特别是这些记录的大部分数据处于无故障的判断结果条件下。所以,在实际构建模糊神经元网络的过程中,需要引入模糊神经元的概念,先对上述输出结果进行折叠和归一化,即对数据进行前置模糊,最终的输出数据,再进行解模糊输出,即可判断出对应的判断结果。
以6 000条测试数据为例,如果对其进行三维折叠,则可形成一组18×18×19的三维矩阵,对上述矩阵进行归一化处理后,可以得到一组18×18和一组18×19的归一化二维矩阵,进一步归一化后,可得四列分别为18、18、18、19单元的归一化评价结果,对这些结果进行神经元网络分析,可以在深度卷积条件下实现对数据的二值化输出,最终为判断结果提供待解模糊计算的一组投影在(0,1)区间上的双精度浮点结果(Double)。详见图4。
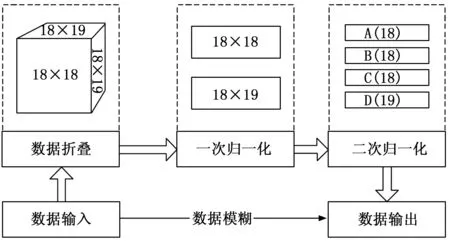
图4 数据的模糊过程
图4中,数据归一化算法的计算过程是首先获得该列数据的最大值和最小值,根据该列数据的最大值和最小值对每个单元数据求取线性投影,进而将该线性投影值累加,从而得到该列数据的归一化结果,即:
(2)
式中:数列A的min值与max值与相邻数列无关,如果该数列中最大值最小值均为0,则输出值R的输出值必为0。
鉴于该模糊矩阵,本文模糊神经网络的设计策略如图5。

图5 本文模糊神经元网络模块设计示意图
如图5中,布尔差分算法模块详见图3,前置模糊模块详见图4,其他模块将在下文中进行分析。该设计中,当使用布尔差分算法认定为故障芯片时,系统将不再启动模糊神经元网络的分析,可以节约大量的计算时间和计算资源。
3 神经元网络软件模块的细部设计
3.1 神经元网络的卷积策略设计
本文设计的前置模糊策略对输入数据进行了大幅度压缩,导致个案中约6 000条数据的数据输入量被压缩到A、B、C、D四个数列共73个双精度浮点变量中,所以,其数据模糊过程属于典型的熵增耗散过程。该过程使大部分数据实现了归一化和去量纲化,数据丢失量较大,所以需要对输入数据进行充分卷积,才可以实现对数据细节的深度挖掘。详见图6。
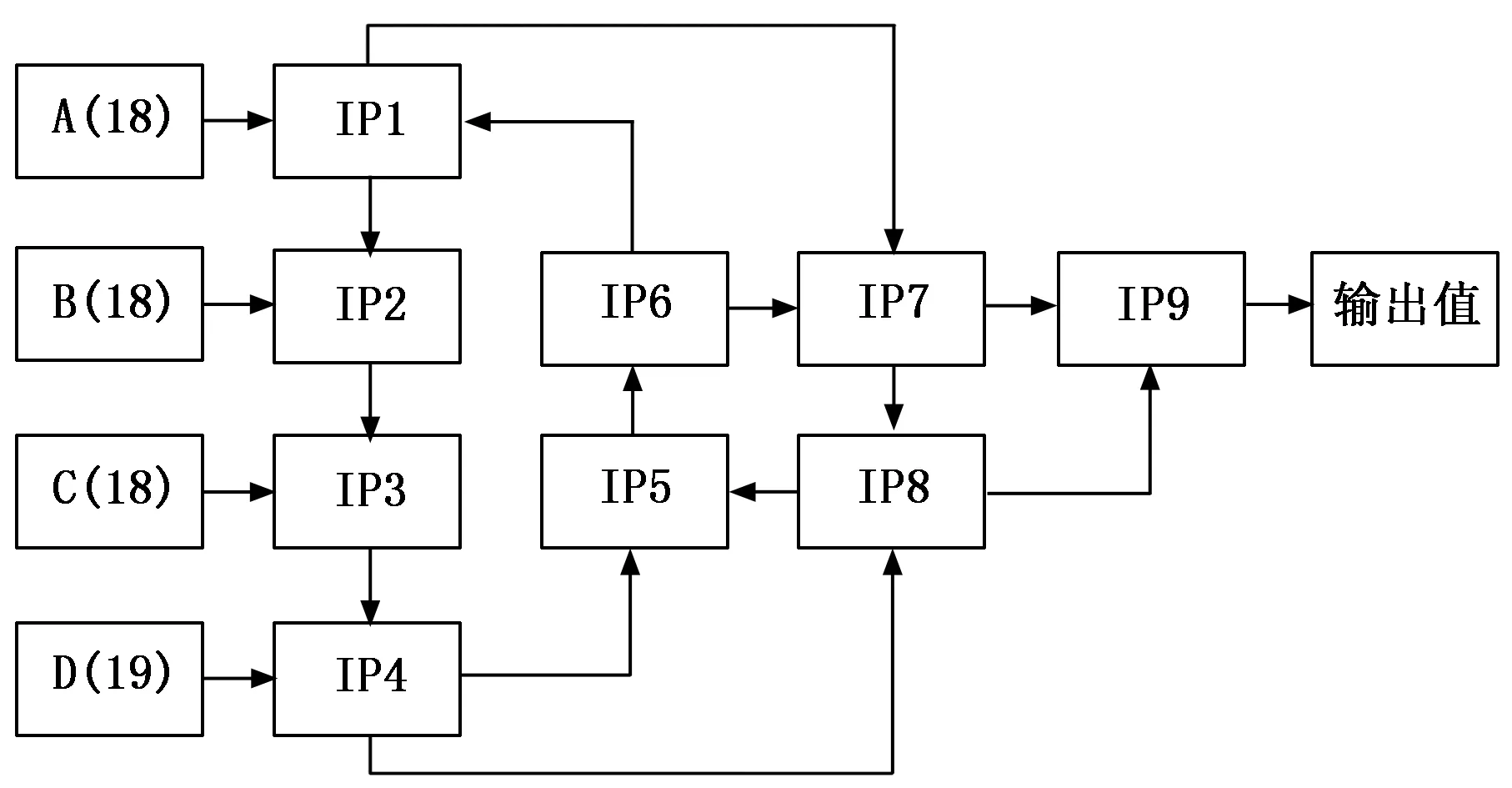
图6 神经元网络的卷积模式设计示意图
图6中设计了两个卷积循环,其中神经元网络模块IP1-IP6构成第一重卷积循环,IP1负责采集数列A信息,IP2负责采集数列B信息,IP3负责采集数列C信息,IP4负责采集数列D信息,在数据卷积过程中完成信息采集,而在神经元网络模块IP5-IP8中进行第二重卷积循环,其中IP7负责整合IP6及IP1的输出量,IP8负责采集IP7与IP4的输出量,与IP5和IP6构成卷积循环后,整合IP7与IP8的输出信息,构建数据输出模块IP9,输出一个二值化数值。
文中,IP1至IP8的神经元模块隐藏层结构相同,仅输入层结构因为输入需求的不同各有不同,其中IP1至IP4的输入节点数较多,分别为待输入的18~19个归一化结果值,均为双精度变量,外1个卷积值,同样为双精度变量。而IP5~IP8均为两个内部卷积数据的输入,均为双精度变量。所有神经元网络的输出变量均为1个双精度变量,需要同步向多个模块提供数据支持的,将同一个输出变量值同时分发到对应的模块中。
该8个神经元模块的中间层均按照4层设计,分别为23节点、17节点、7节点、3节点,输出层均为1节点。而IP9神经元模块采用5层中间层设计,分别为3节点、11节点、23节点、7节点、3节点。
3.2 神经元网络的节点函数选择
首选分析神经元模块IP1-IP8的节点设计方式。在统计学意义上,该8个神经元网络模块的统计学意义均为充分挖掘数据细节,使数据细节得到充分展现,故其所有节点均可采用多项式函数进行迭代回归管理。其节点函数为:
(3)
式中,Xi为输入序列的第i个输入结果;j为多项式阶数;Aj为第j阶多项式的待回归变量;Y为该节点的输出值;
神经元模块IP9的统计学意义在于将接近于0值的判断结果尽可能后移,但不能打破所以数据点投影的位置相对序列关系。在其输出层需要构建一个二值化层,确保最终数据投影在(0,1)区间上。故IP9的隐藏层节点函数应为对数函数:
Y=∑(A·logeXi+B)
(4)
式中:A为该对数函数的斜率校正值的回归结果;B为该对数函数的截距校正值的回归结果;e为自然常数,用作对数底值,此处取近似值2.718 281 8;Xi为输入序列的第i个输入结果;Y为该节点的输出值;
IP9模块的输出层应采用二值化函数进行管理,其节点函数为:
(5)
式中,A、B为该函数的待回归变量;e为自然常数,用作幂底值,此处取近似值2.718 281 8;Xi为输入序列的第i个输入结果;Y为该节点的输出值;
对上述节点设计进行统计,整合模块设计的结果,可以得到该神经元网络模块的总设计架构,详见表2。
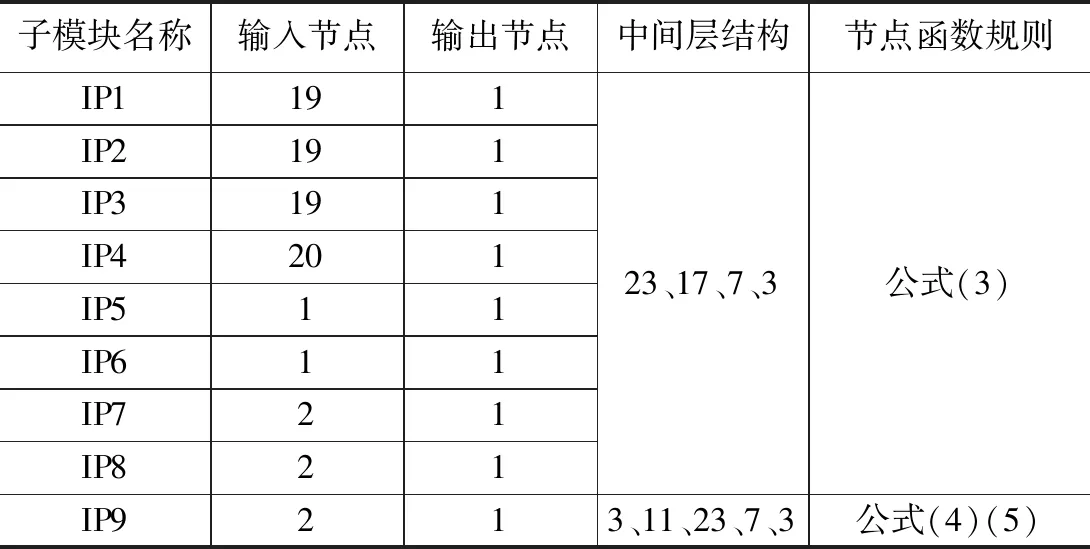
表2 神经元网络各模块的设计参数汇总
4 系统测试与测试结果讨论
选择40片MC6821集成电路与40片MAX7219芯片作为测试芯片,经过前期全面工程测试,每组芯片均为20片故障芯片与20片正常芯片,分别使用升级前算法RC1算法与升级后的RC2算法进行芯片故障测试。其测试结果如表3所示。

表3 算法升级前后的测试效果统计表
表3中可以看到,算法升级后的模糊神经元网络算法合并布尔差分算法的RC2算法,相比较单纯使用布尔差分算法,其测试敏感度从84.2%提升到95.2%,其测试特异度从81.0%提升到100%,所有测试结果经过SPSS信度分析,P<0.01,具有显著统计学意义。故可认为,升级后的算法测试能力显著优于升级前算法。
但是,该算法仍存在一些不足,这一不足体现在升级后算法不能完全排除将正常芯片认定为故障芯片的可能,即使用新算法的系统仍可能对无故障芯片发生误报。此时,建议对同一芯片进行2次以上的测试,最终2次以上测试解决均相同时,认为测试结果有效。
传统的基于工程分析的芯片测试工作往往需要耗费大量的时间成本和人力成本,特别是大规模硬件开发工作中,因为使用芯片较多,很难在整体硬件功能出现问题时找到问题原因。这也是类似航空航天等高复杂度系统出现问题后,故障排查周期可能长达数月甚至数年的主要原因。开发一种高可靠高可用高效率的集成电路故障分析系统,将是解决这一问题的关键。本文升级算法设计后,使得集成电路测试系统的分析效果得到了显著提升,将使高精密高复杂度设备的故障排查工作效率得到显著提升。
5 结束语
本文在传统的数字集成电路故障测试系统中进行深度开发设计,通过选择更高配置的嵌入系统,同时在传统的布尔差分算法的基础上,引入模糊神经网络算法的机器学习功能对不可测故障进行更加精密的捕捉,升级后的算法使该测试系统获得了更精确的测试结果。较以往通过升级优化布尔差分算法测试集以提升测试结果精确度的技术升级方案不同,该方案充分利用系统测试大数据资源,使用机器学习和人工智能概念,让测试过程的诸多不可控性得到了有效控制。

