理性精神的塑造
李铁安 孔玥


这节课源自一条广泛传播的微信:“2020年5月是个不寻常的月份,这个月份中有5个星期五、5个星期六、5个星期日。这种情况需要823年后才能再次出现,这种月份被认为是‘钱币之月。如果把这个消息发送给包括我在内的8位好朋友,4天以后就会有钱币上的收获。”微信内容炫而又炫,玄而又玄。事实上,通过数学的逻辑推理和推演能无可辩驳地判断此条微信的真伪。本节课就是针对这条微信展开教学的,使之成为对学生进行理性精神塑造的一个难得的课程资源。
【教学过程】
环节一:头脑风暴,引出问题——初步感受日历中规律之丰富
师:同学们,开课之始我们先来一场头脑风暴。看,这是2020年3月的日历(出示表1),从中你知道了什么,发现了什么?说得越多越好!
生:2020 年的3月有31天。
生:3月1日是星期日。
生:3月2日是星期一,3月3日是星期二,3月4日是星期三,像这样看下去,7天为一个星期,3月的最后一天3月31日是星期二。
生:我知道3月12日是植树节,这一天是星期四。
生:同学们横着看,3月2日到8日是一个星期,9日到15日是一个星期,16日到22日是一個星期,23日到29日是一个星期,3月一共有4个星期,还余3天:3月1日、3月30日和3月31日。
师:是的。大家接着想,3月30日、31日和4月的哪几天合为一个星期呢?
生:是4月1日到5日。
师:真不错。大家继续说。
生:我竖着观察,发现3月份有5个星期日、5个星期一、5个星期二,而星期三、星期四、星期五、星期六都只有4个。
环节二:探索发现,辨别真伪——深入探究感受规律的意义价值
师:同学们从3月的日历里发现了不少规律。下面,一起来看看老师收到的这条微信。(教师出示上述微信内容)
师:你们怎么看这条微信?
生:我觉得这是迷信,不可信。
生:我想知道5月到底是不是有5个星期五、5个星期六、5个星期日。
师:你很会提问题!下面,我们就来看看5月份到底有没有5个星期五、5个星期六、5个星期日。你们来试着填一填,找一找。
(教师出示一张空白的5月日历,只给出5月1日是星期五的信息,让学生接着把5月的日历填完整,如表2。教师巡视指导)
师:结果怎么样?
生:真的是5个星期五、5个星期六、5个星期日!
师:看来,这条微信讲的是真的了。让我们一起转发这条微信,来期待“钱币之月”带来的好运吧!(停顿片刻,等待学生的思考判断)
生:我觉得这条微信还是有问题,难道一个月份里有5个星期五、5个星期六、5个星期日,就一定会带来钱币的收获?这和钱币有什么关系呢?我想这一定是有的人想让我们多发微信,故意这样说的。
生:我想知道这种情况真的要823年后才能再次出现吗?
师:不轻信,敢质疑,非常好!是啊,这种现象出现的可能性真的那么小吗?下面,我们就来试一试,看看有没有其他月份也会在一个月里出现5个星期五、5个星期六、5个星期日?
(小组合作学习,教师巡视指导)
师:哪个小组来汇报?
生:我们小组四人分工把一个月的第1天分别写在星期日、星期一、星期二、星期三的位置,然后按照一个月有31天往下填,结果都没出现5个星期五、5个星期六、5个星期日。
师:那你们填好的日历是什么情况?
生:我把第1天写在星期日的位置,填完了发现这个月有5个星期日、5个星期一、5个星期二;我同桌把第1天写在星期一的位置,得到的是5个星期一、5个星期二、5个星期三;我后面的同学把第1天定为星期二,出现了5个星期二、5个星期三、5个星期四。我们组最后一名组员把第1天填在星期三的位置,出现的是5个星期三、5个星期四、5个星期五。我们还想把第1天填在星期四和星期六的位置试一试,可惜时间到了,没完成。
师:你汇报得非常清楚。你们组按顺序尝试的方法也非常好。那有没有哪个小组把第1天填在星期四、星期五或星期六的位置呢?
生:我们组做了,把第1天填在星期四或星期六的位置,也没有出现5个星期五、5个星期六和5个星期日。但是,把第1天放在星期五的位置,就出现了5个星期五、5个星期六、5个星期日。
师:看来,经过我们验证,出现“钱币之月”只有一种可能,就是那个月得是大月而且第1天是星期五!大家想想,这是为什么呢?
生:如果是小月,到30日为止,就只有5个星期五、5个星期六,不会有5个星期日了。
生:算也能算出来。你们看,大月有31天,一个星期有7天,31除以7,商4余3。商4说明这个月里有4个整星期。这样从星期一到星期日都会各有4天。剩余的3天,就说明肯定有3个星期几是5天。如果零的3天正好是星期五、星期六和星期日,那就说明这个月有5个星期五、5个星期六、5个星期日了。但如果是小月,30天除以7后,余数是2,就只能有2个星期几是5天了,一定不会出现所谓的“钱币之月”。
师:你分析得井井有条!原来通过计算也能说明这个问题!因此,要出现所谓的“钱币之月”,必须是在大月,这个月的第1天还得是星期五。那么同时具备这两个条件的可能性有多大呢?真的需要我们等待823年才能再遇上一次吗?(故弄玄虚地停顿)
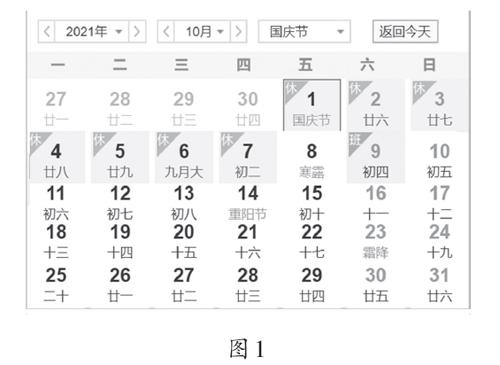
师:其实,人们已经推算出来了。你们看,2021年的10月份就会出现5个星期五、5个星期六、5个星期日(出示图1)。我们并不需要等八百多年那么久!同学们,你们现在想说点什么?
生:原来“钱币之月”的说法是个谎言,幸好我们没上当啊。
生:我要告诉妈妈这条微信的真相,不让她被骗。
生:数学真有用,可以帮我们判断真假。
师:是的,数学是一门严谨的科学,它容不得半粒沙子。
环节三:拓展运用,迁移推算——活化规律的应用延伸数学思考
师:刚才,同学们在辨别微信真伪的过程中,对日历中星期的分布规律有了更多的认识和发现。下面,我们再来挑战一组日历中有趣的问题。
教师出示问题:
1.2020年5月有5个星期五、5个星期六和5个星期日,那么2020年6月会有几个星期六呢?
2.根据2020年5月的日历,你知道2020年4月20日是星期几吗?
3.某年12月20日是星期日,那么这一年的12月一共有几个星期日呢?
(学生可以自主选择题目和学习伙伴,合作完成,然后汇报交流,过程略)
师:同学们已经能够运用日历中的规律游刃有余地解决问题了!关于日历中的数学问题你们还有什么想说的或想问的?
生:我发现原来日历中有这么多数学奥秘!
生:我知道了为什么有的月有3个星期几是5天的,有的月只有2个星期几是5天的。我还想到如果是2月,平年2月28天,闰年2月29天,情况又会不同了。
师:你想得真全面。
生:我会根据一个日期是星期几,推算出另一个日期是星期几了。
生:我还想知道1年里星期是怎么排列的。
生:我想探究在2021年之后,还有哪一年的10月也有5个星期五、5个星期六和5个星期日。
【育人意蕴解析】
这是一个知识和信息可以无限爆炸并横空出世的时代,这也是一个时时处处事事人人都可以产生信息和创意并恣意散布的世界。如果说“辨识真伪”是当下这个时代和这个世界给每个人设置的一个“必答题”,那么以“理性精神”去“辨识真伪”或许是正确解答这个“必答题”的锐利武器。而对于那些充满天真好奇的儿童来说,培育他们以“理性精神”去“辨识真伪”的意识和素养就显得更为必要而迫切!
这是一个彰显数学文化价值和育人力量的经典案例。首先,教师充分挖掘了微信内容中蕴含的数学抽象、逻辑推理等育人价值,以及借助理性思考明辨是非的人文内涵,为学生提供了一个充满文化魅力的数学学习题材。本节课的核心问题是判断“2020年5月有5个星期五、5个星期六、5个星期日,823年后才能再次出现这种情况”这条微信的真伪。其次,围绕核心问题,教师精心设计了子问题,搭建了既循着学生认知规律螺旋而上又符合数学内在规律的问题结构,为学生追根溯源、思维攀升巧妙引路。具体的子问题是:①从2020年3月的日历中你知道了什么,发现了什么?②2020年5月到底是不是有5个星期五、5个星期六、5个星期日?③这种情况真的要823年后才能再次出现吗?④这样的月份有什么特征?⑤如何看待这样的微信?⑥如何解决日期、星期前后推算的问题?⑦关于日历、月份、星期等,你还能提出哪些有趣的问题?
问题①是激趣式引入与铺垫,旨在引发学生对日历中相关数学信息的观察和发现,培养学生的数学眼光和直觉意识。问题②~⑤的探究直接指向要解决的核心问题。问题②是基于数据做出直观的判断,旨在培养学生数据分析的意识与能力;问题③是适时的追问,旨在培养学生的质疑精神和反思能力;问题④蕴含了数学运算、数学建模、数据分析、逻辑推理与抽象的思想,启发学生对数学问题以更高阶思维进行抽象建模的数学观念,旨在引导学生透过现象提取本质,培养学生的高度抽象思维能力和数学建模能力;问题⑤启发学生再次追问,旨在培养学生借助理性思维做出判断的意识和能力。问题⑥和⑦蕴含了数学问题解决中思维的迁移和拓展性,也蕴含了数学运算、数据分析、逻辑推理与抽象的思想,旨在激发引导学生从不同的角度审视问题并开拓问题解决的路径,提升学生数学问题解决的创造性思维。综观本课问题解决的过程,在逻辑架构和解决路径探究中,教师巧妙地将抽象、推理、转化、对应、分类等数学思想融入其中,也巧妙地将数学抽象、数学建模、逻辑推理、数学运算和数据分析等数学思维方式植入并贯穿在学生的问题解决过程中,不露痕迹又事半功倍地引领学生经历了一场提升数学理性思维能力的文化之旅。
再细细品味课堂中教师对学生的评价语,语言简练但很有激励性和启发性。如“不輕信,敢质疑,非常好!是啊,这种现象出现的可能性真的那么小吗?”“你汇报得非常清楚。你们组按顺序尝试的方法也非常好。”“是的,数学是一门严谨的科学,它容不得半粒沙子。”“真不错。你能够边计算,边推理,真善于思考。”这些充满爱的鼓励,营造了一种安全愉悦、互相尊重、互相欣赏的课堂文化氛围,使学生兴趣浓厚地沉浸在解决问题的过程中,更有利于学生全情投入思考,迸发创造性思维,这种隐形的文化的力量也是很宝贵的。
总而言之,本节课教师将这份课程资源运用得淋漓尽致,让学生在环环相扣、层层递进的问题探究过程中,经历有趣、有用、有力的数学思考过程,这也正是学生理性思维不断走向深入的过程。而在此课例中学生不仅积累了丰富的数学思想和数学活动经验,而且提升了问题解决能力和创造性思维能力。
随着问题的逐一解决,这条微信的真相也逐渐浮出水面,学生是多么享受这个通过自己独立思考、合作探究而辨其真伪的数学学习过程啊!数学之美与数学之真,不仅展现于有形处,更幻化于无形处,这便是思维的力量。学生理性精神的塑造过程,正是教师引领学生享受数学独特文化魅力的过程。
(中国教育科学研究院基础教育研究所 100088辽宁省大连经济技术开发区红梅小学 116600)

