多级回转体装配偏差建模方法综合研究

丁司懿，郑小虎，鲍劲松，张 洁

(东华大学 机械工程学院，上海 201620)

随着世界航空工业的发展，我国加快了新型飞机自主研发的进程，如我国自主设计制造的支线飞机ARJ21、中短程双发窄体民用客机C919以及中俄联合研制的远程宽体客机C929等[1]。然而，我国航空工业基础相对薄弱，在商用大型飞机发动机方面仍是空白[2]。ARJ21和C919所采用的发动机分别是美国GE航空集团所研制的CF34-10A型发动机和法美合资公司CFM所研制的LEAP-1C型发动机。为了促进飞机自主研发，我国实施“中国制造2025”战略，将大型飞机发动机项目列入制造业转型升级的重点领域[3]，以充分发挥航空发动机产业为国民经济和科技发展所带来的推动作用。

航空发动机装配是整机制造全过程的关键环节，转子组装则是整个装配环节的核心[4]。如果转子的定心方案设计不妥、装配不当、平衡不好，转子服役时会产生剧烈振动，直接影响整机的安全性。转子组件由鼓盘式回转体零件构成，如图1所示，其具有刚性大、止口定位约束多、螺栓连接过程繁复、级间层次关系复杂等特点[5]。

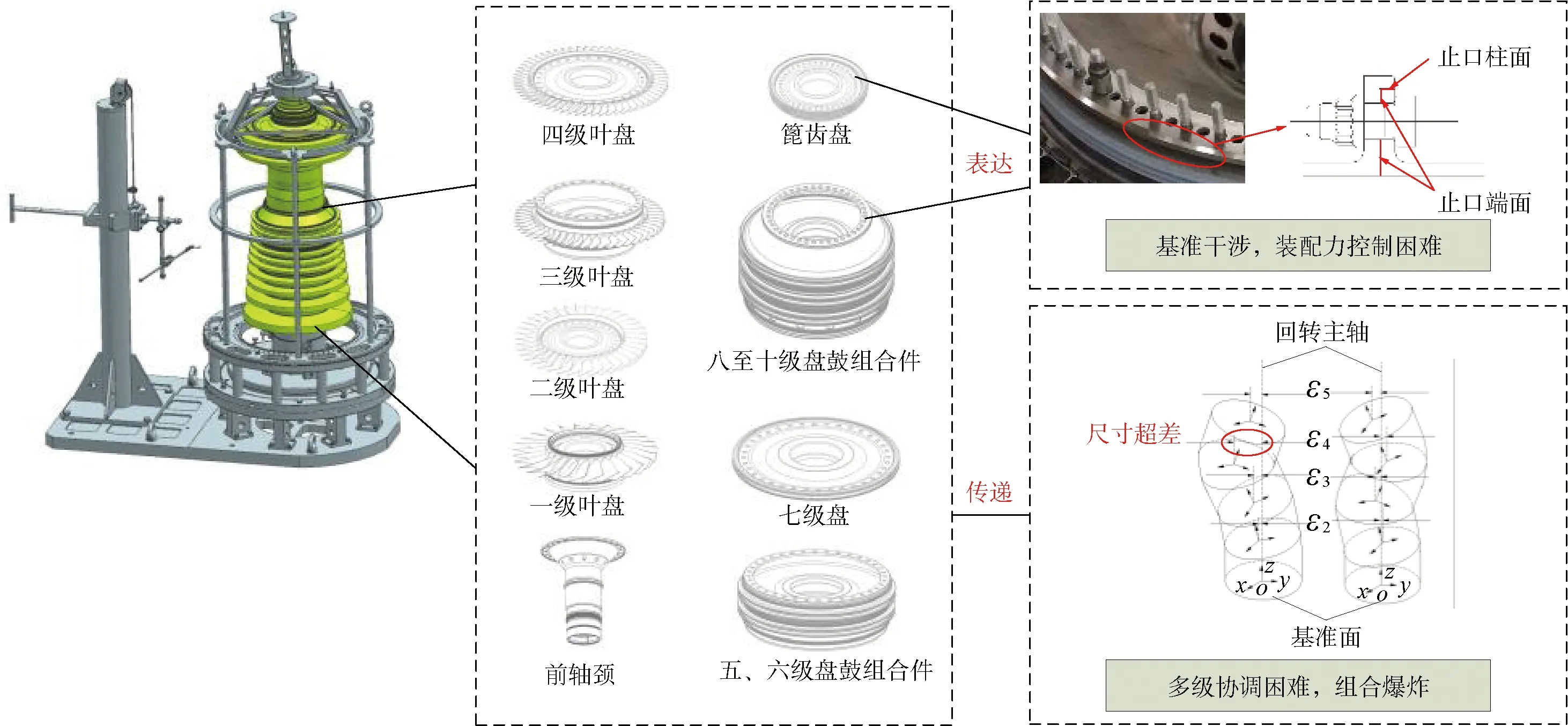
图1 高压压气机转子堆叠Fig.1 High-pressure compressor rotors stacking

多级转子装配精度控制的核心问题在于偏差表达和偏差传递。在偏差表达方面，实际转子装配一般采用止口定位连接方式。止口结构同时包含一对平面副和一对圆柱副，使偏差在传递路径上形成局部并联回路，因此，传统针对局部特征的串联表达方法不再适用于该类型的装配连接关系。在偏差传递方面，现有的偏差控制手段多聚焦于平面尺寸链建模和极值法分析，难以综合考虑连接特征上丰富的形位偏差信息及其相互影响关系；整机装配精度预测过于保守，过分侧重零件自身加工精度的提升，忽略了组件整体堆叠优化的手段，而增加零件返工频率和修配难度。

航空发动机转子装配精度控制与工艺系统设计仍缺乏有效的理论方法，装配偏差分析合理性有待改善，多级安装调控效率有待提高。通常一次成功的装配需要4～5 d，反复拆装4～5次，零件反复经历冷热加工，这些都极大影响了转子的寿命。因此这种装配方式已经无法满足现代航空发动机制造的需求。

装配偏差分析是精度控制和预测的有效手段，通过建立定量描述几何偏差在装配过程中传递关系的数学模型实现对装配精度的定量分析和预测。国内外众多学者围绕航空发动机转子装配的偏差表达和偏差传递两大核心问题进行了深入探索，最新的转子装配三维偏差理论主要从两个方面展开：一方面是偏差表达，从局部偏差表达的角度解决多对基准特征复合定位问题；另一方面是偏差传递，从尺寸链的角度构建整机偏差传递模型。下面将针对这两方面进行详细论述。

1 转子局部特征的偏差表达模型

针对转子局部特征的偏差表达有：Zeng等[6]区分并列举了所有局部连接副类型，以螺旋锥齿轮变速箱为对象，总结了5种常见的局部过定位结构；Yang等[7]系统探讨了回转体堆叠过程中连接特征的偏差表示方法；丁司懿等[8]提出了基于REM-GA法的几何特征提取拟合技术，用试验手段论证了该方法的可行性，但对转子局部止口的构造和求解都过度简化，预测值和实测值存在较大误差；为了量化转子局部并联链的效用，Chen等[9]针对发动机曲柄连杆机构进行了分析验证，结果表明转子止口定位结构对求解精度有显著影响，不能轻易忽略。由此可以看出，传统做法是将上口安装边上的止口柱面特征忽略，而仅考虑偏差在止口端面上的表达和传递。这样做虽然可以把转子局部并联关系转化为单一方向的串联关系，找到唯一的偏差传递路径，简化计算，但不可避免地造成了大量几何偏差信息和物理约束关系的损失，难以有效地表达由形位偏差引起的特征变动以及尺寸偏差和形位偏差之间的耦合关系。同时，局部并联结构形式多样，目前没有一个通用的方法来构造局部并联链的连接特征，这会导致分析结果的不一致性。转子局部特征表达的最新方法主要可归纳为以下4种：布尔代数运算法、局部公差接触影响法、接触点偏差求解法、有限单元法。

1.1 布尔代数运算法

Chen等[9]通过将布尔运算(boolean algebraic operations， BAO)规则引入雅克比旋量模型中，提升和改进了雅克比旋量模型处理局部并联链的能力，对构成局部并联回路的装配特征的独立旋量表达式进行统一合并，推导出一个新的涵盖整个局部特征的旋量模型，从而实现局部并联链向纯串联链转变的同时，保证不会丢失细节特征偏差源。此外，为了避免新旋量中的冗余偏差，需要判别各独立旋量是否含有矢量重叠，如果有重叠则进行布尔“交”运算，如果无重叠则进行布尔“并”运算。Chen等[9]借助以上过程，对存在局部并联结构的复杂装配体连接特征旋量表达进行了完善。

旋量合并：

(1)

式中：Tp为局部特征旋量；T1为特征一旋量；T2为特征二旋量；u、v和w分别为局部坐标系中沿x、y和z轴方向的移动矢量；α、β和γ分别为沿x、y和z轴的转动矢量。

矢量判别：

(2)

式中：Vp为局部特征矢量集；V1为特征一矢量集；V2为特征二矢量集；Vu、Vv和Vw分别为局部坐标系中沿x、y和z轴方向的移动矢量集；Vα、Vβ和Vγ分别为沿x、y和z轴的转动矢量集；Vu1、Vv1和Vw1分别为特征一局部坐标系中沿x、y和z轴方向的移动矢量集；Vα1、Vβ1和Vγ1分别为特征一局部坐标系中沿x、y和z轴的转动矢量集；Vu2、Vv2和Vw2分别为特征二局部坐标系中沿x、y和z轴方向的移动矢量集；Vα2、Vβ2和Vγ2分别为特征二局部坐标系中沿x、y和z轴的转动矢量集；符号“П”代表着“∩”或“∪”操作，取决于参与布尔运算的两组旋量其矢量之间是否有重叠。

整个合并过程是针对特征集合来进行的，因此该方法更适合统计公差分析，在确定性偏差分析中还存在一定局限性。同时，大量的“交”“并”操作使运算效率较低，过程较繁琐。

1.2 局部公差接触影响法

Chavanne等[10]提出局部公差接触影响(localization tolerancing with contact influence， CLIC)法用以解决局部特征接触时公差的表达和重构，通过模拟一组含有极端偏差接触点的虚拟边界面避免局部特征干涉，以此计算累积公差，具体方法如图2所示。首先对可能发生干涉的功能特征副进行判别，提出备选妥协方案；其次在满足最大功能要求的前提下赋予名义尺寸极值公差；最后在满足最优成本的前提下来筛选最大化公差。CLIC法更多强调装配体几何结构的杠杆效应，在求解转子止口配合的确定性偏差问题上还存在一定局限性。

Benichou等[11]在CLIC法基础上考虑了热膨胀效应对功能尺寸的影响，比较了公差量、热膨胀量以及温度幅值在偏差链中的重要次序。

图2 局部公差接触影响法[10]

1.3 接触点偏差求解法

Jin等[12]通过在传统的旋量理论中引入基于接触点偏差求解(contact points-based solution， CPS)法表达的小位移旋量模型，构造出适合航空发动机转子接触特征的三维偏差表达模型。具体过程：首先考虑装配基准的主次关系对偏差源进行顺序化分组，然后构建以点接触形式来表示的偏差旋量，最后将所有定位点视为一个独立的装配系统，推导出一般形式下的装配偏差表达函数。

来源于主基准面上的偏差：

(3)

式中：δRh1为主基准定位点偏差；δEm和δEr分别为主基准定位点和零件的SDT偏差；[J]m和[J]r分别为主基准定位点和零件的雅克比矩阵。

来源于副基准面上的偏差：

(4)

式中：δRh2为副基准定位点偏差；δEd为副基准定位点的SDT偏差；[J]d为副基准定位点的雅克比矩阵。

含有m个不完全定位点的装配偏差：

(5)

式中：δRi为第i个定位点偏差引起的转子偏差。

接触点偏差求解法针对宏观刚性零件建模，将所有定位点视为一个独立的刚体装配系统，无法考虑介观偏差的影响。

1.4 有限元法

李伟楠等[13]提出了盘类转子堆叠柔性工装，利用有限元法(finite element method， FEM)求解了不同载荷工况下工装变形情况，讨论了影响工装定位精度的主要偏差源，提出了定量补偿方法，如图3所示。

图3 航空发动机转子柔性工装[13]Fig.3 Flexible clamping fixture of aero-engine rotors[13]

文献[14-15]提出了波动有限元理论，研究了航空加筋壳体零件的带隙特性，并对其进行了隔振设计，获得了气动载荷作用下的最优平面外带隙和整体结构质量，同时利用非线性有限元接触分析方法对高速可拆卸转子止口连接结构进行了稳健性设计，围绕如何增大止口处局部刚度和设计紧度配合等问题提出了有效地措施。Andersson[16]建立了超音速涡轮叶片的有限元模型，讨论了制造偏差对超音速涡轮效率的影响，确定了造成影响的主要敏感参数。Forslund等[17]研究了涡轮后机匣相对于装配基准点的功能稳健性，指出几何偏差会带来结构应力及热应力的消极影响，如图4所示。

图4 涡轮后机匣安装边[17]Fig.4 Mounting surface of turbine casing[17]

利用有限元法可以得到从整体到局部、从静力分析到复杂工况下详实的模拟结果，但总体过程建模难度大，求解效率低，更适合作为其他解析模型的辅助验证性方法。因此，需要一种针对止口并联结构的偏差建模及求解方法，使装配偏差分析模型能够充分考虑各个特征的影响。

2 多级转子堆叠的偏差传递模型

国内外学者普遍从三维尺寸链角度建立特征偏差与功能要求之间的映射关系。随着航空发动机装配工艺的发展和完善，其装配理论方法从传统的平面尺寸链模型[18-19]发展到二维直接线性化模型[20]，再衍生出广泛的三维偏差传递模型[21-24]，装配偏差建模方法得到了跨越式的完善和改进。运动方程模型[25]、公差域和基准网络模型[26]以及空间尺寸链模型等[27-28]，这些模型虽然体现了偏差的几何涵义，是偏差分析技术的基础，为后续三维偏差理论研究指明了方向，但是其无法处理装配体的方向和形状偏差。此外，因这些模型的偏差类型过于单一而没有得到进一步的发展和应用。随后发展起来的偏差理论主要有变分模型[29]、旋量模型[30-32]、齐次矩阵变换模型[33]、三维直接线性化模型[34]、公差映射图模型[35-36]、雅克比模型[37]和雅克比旋量模型[38]等，这些理论是当前偏差分析的研究热点[39-42]，也是真正意义上的三维偏差理论模型。近年来，一些学者对新兴的多色集合模型[43]、最短路径图模型[44-45]也相继展开了研究，不断地对三维偏差分析技术进行探索。转子偏差传递建模方法主要可归纳为以下5种：直接线性化模型、连接装配模型、确定性定位模型、雅克比旋量模型、试验法。

2.1 直接线性化模型

Wittwer等[46]采用一阶泰勒级数展开式将非线性尺寸链进行线性化处理，再利用7种运动铰链对零件相对装配关系进行描述。图5建立了某滑块装配体的二维矢量环[47]，通过依次求解装配矢量环各段的一阶偏导，可以构造出装配偏差对尺寸偏差的敏感度矩阵，从而计算出装配偏差累积量。

图5 二维矢量环模型[47]Fig.5 2D vector loop modeling[47]

直接线性化模型(direct linearization model, DLM)仅考虑了几何偏差对装配结果的影响，忽略了介观尺度的效果,更适合描述偏差传递过程，无法做到其表达和传递的统一。

2.2 连接装配模型

Hussain等[48]利用连接装配模型(connective assembly model, CAM)提出了直接装配和平行装配两种偏差控制方法，对航空发动机转子堆叠进行了最佳同心度控制和最佳安装角设计，较好地考虑了几何偏差的传递。CAM是利用机器人学[49-53]中的3×1矩阵平移和3×3 矩阵旋转来描述特征偏差在三维空间里的变动[54]，具体如式(6)所示。

(6)

式中：u、v和w分别为局部坐标系中沿x、y和z轴方向的移动矢量；α、β和γ分别为沿x、y和z轴的转动矢量。

文献[55]列出了7类典型特征的矩阵表达式，该表达式中各矢量的约束关系与偏差类型及其配合面形状有关。假设某特征i仅含有一种类型偏差源，则该偏差的合理变动范围如式(7)所示。

tSL≤(Di-I)[Lj]RiX≤tSU

(7)

式中：X为目标特征方向矢量；tSU与tSL分别为特征i的上、下极限偏差；[Lj]Ri为第j个偏差点在特征i上的位姿坐标。

式(7)为偏差矢量之间的约束方程。由此可以看出，约束方程随着偏差点数目的增加而增加，偏差点越多，计算量越大，但预测结果越可靠。如果特征i上还存在复合偏差，那么还需要结合矢量偏差的类型，进一步增加矢量约束方程，此时会使计算过程异常费时。

CAM主要基于齐次坐标矩阵变换理论，利用一组约束不等式对目标点最佳位置进行优化，其求解效率及运算精度受制于组件的装配复杂度及优化算法。

2.3 确定性定位模型

确定性定位模型(deterministic locating model， DeLM)是一种基于离散点接触式的偏差传递模型，在零件空间六自由度完全受到约束的情况下描述定位点制造偏差和零件定位偏差之间的关系，如图6所示。

图6 确定性定位模型[56]Fig.6 Deterministic locating model [56]

DeLM的应用基础是保证零件的定位约束方程得以唯一确立，同时零件自由度处于完全约束之中。该模型有助于分析复杂三维偏差传递问题，其具体表示如式(8)所示。

δq0=-J-1ρRδR

(8)

式中：δq0为零件完全定位后的位姿偏差；δR为6个定位点的制造偏差；J为定位偏差对夹具偏差在全局坐标系中的传递关系；ρR为定位偏差对夹具偏差在局部坐标系中的传递关系。

Cai[57]结合线性变分法推导出了DeLM的函数表达式，揭示了定位点制造偏差和零件定位偏差之间的关系。但在零件空间六自由度完全受到约束的情况下，如何根据具体特征的限位作用进行定位点选取的统一规范，是目前亟待解决的问题。

2.4 雅克比旋量模型

J-T模型(Jacobian-Torsor model)综合运用了适合偏差传递的雅克比矩阵及适合偏差表达的旋量模型，其具体表达如式(9)所示。

[R]6×1=[J]6×6[E]6×1

(9)

式中：[R]为6×1的功能要求列矩阵，表示目标特征偏差量；[E]为6×1的功能单元列矩阵，表示传递特征偏差量；[J]为6×6的雅克比矩阵。

J-T模型结构简单，数学表达清晰，工程语义丰富，可以充分考虑尺寸、形位偏差的表征，所以其计算结果相对于传统偏差分析方法更加精确、可靠。Cao等[58]结合旋量理论和状态空间法对航空发动机转子装配精度进行预测，并提出误差补偿方法，然而该方法仅针对加工补偿，并非实际过程的装配调节补偿，实用性有限。Ding等[59]对雅克比矩阵进行扩展，构造偏差在特征高度和特征角度上的传递路径，揭示了转子组件的多级回转特性和偏差联动效应，但该模型无法表达确定性并联几何偏差和局部变形特征。

2.5 试验法

陈志英等[60]利用改进田口试验法，结合皮尔逊理论分析了涡轮转子偏差分布非正态情形，计算效率较蒙特卡洛法有了明显提高，但偏差样本少，概率分布依赖人为假设。Pierce等[61]提出了模拟试验法(design of experiment, DOE)，对实测点云数据进行B样条曲面拟合，引入加工方式变量并结合罚函数法将约束优化问题转化为无约束问题，计算出“最佳匹配过程中的最小距离”，如图7所示。

图7 Generate-and-Test公差分析法[61]Fig.7 Tolerance analysis method of Generate-and-Test[61]

Generate-and-Test公差分析法以相邻配合面随机偏差扰动的假设为前提，难以准确预测多级转子之间的接触效果。因此，现有的偏差传递模型还难以完全满足航空发动机回转体零件的装配精度分析的需求，有待进一步完善。

3 结 语

近年来航空发动机转子装配发展了很多新理论、新方法，本文从应用对象及偏差类型、求解方法及效率、工程应用、算法难易程度等方面综合比较了几种典型偏差模型，如表1所示。现有针对航空发动机转子装配的三维偏差分析模型，主要从局部偏差表达的角度解决多对基准特征复合定位问题，以及从尺寸链的角度构建整机偏差传递模型两个方面进行论述。

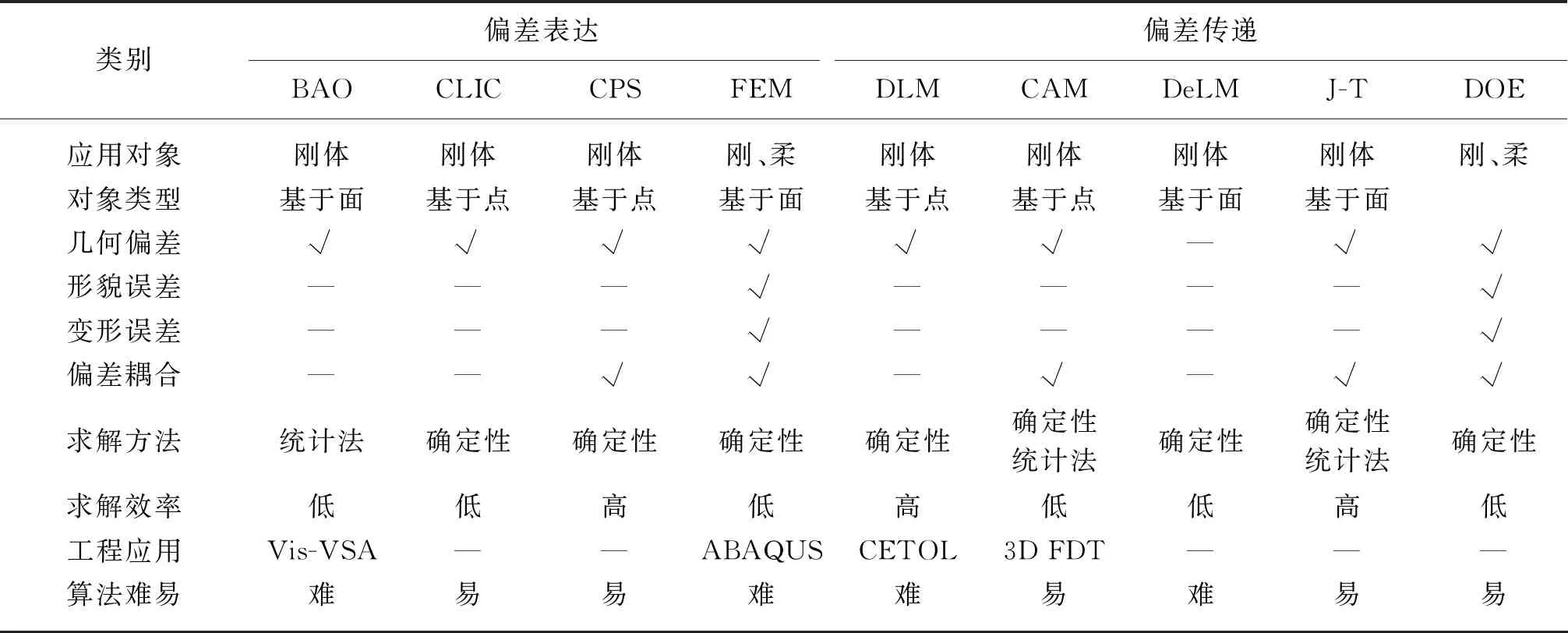
表1 典型偏差模型比较

综合本文分析，可以得出：

(1) 针对传统转子装配过程，很多学者对偏差表达方法、传递机理、控制策略等方面开展了大量的理论和试验研究，形成了较为完善的理论体系和研究方法。但目前的偏差模型还不能考虑局部并联、多级传递与耦合、装配力等重要的装配偏差影响因素，无法满足整机装配精度要求。

(2) 在局部特征偏差表达方面，实际建模时一些细小特征被忽略，如止口结构中的短小柱面将局部并联尺寸链转变为更易于求解的普通串联尺寸链，但这样的简化操作会导致实际应用时准确性、可靠性较差。在整机尺寸链偏差传递方面，目前的偏差传递模型多聚焦于单一方向的串联尺寸链建模，无法解决并联、局部并联以及混合尺寸链的偏差传递问题，同时组件整体同心度的偏差联动效应和旋转控制方法也无法在这些模型中体现。

(3) 一个合理的偏差传递模型可以得到更为精确的分析结果，既对回转组件同心度超差问题进行准确描述，又可以综合考虑由几何偏差引起的特征的三维变动及其与尺寸偏差的耦合关系。此外，能够针对确定性偏差问题提出有效堆叠方案，区分量化所有参与计算的偏差源的贡献程度，并对关键零部件偏差进行分类管控。因此，必须把对偏差表达和传递机理的研究作为重点，为转子设计和装配工艺提供指导。

4 展 望

后期研究中应结合最新的偏差理论，在以下几方面寻找新的突破，以完善转子装配偏差分析的理论体系方法，促进我国转子装配技术进一步发展。

(1) 考虑转子变形条件下的三维偏差建模。现有的三维偏差模型主要以刚体假设为基础进行分析，未能考虑转子系统实际工况的影响，例如忽略了螺栓预紧、过盈压紧等因素导致的转子局部变形误差。为了提高模型的精度，本文所列举的方法在运用于实际转子堆叠时，需要考虑更多变形误差的影响，通过引入装配工艺参数、真实边界条件等方式来进一步修正偏差传递模型，以获得更加准确、可靠的分析结果。

(2) 形貌误差的表达及匹配。本文所列举的方法描述某个装配特征在结构拓扑层、偏差要素层下的位姿偏差，却无法描述特征在微观形貌层的偏差状态。零件形貌误差的存在导致了转子装配过程中的不完全匹配现象，对最终同心度控制造成实质性影响。因此，对于航空发动机转子这类精密回转件，若能在考虑其尺寸、位置和方向偏差的同时，进一步考虑其形貌误差的表达和匹配，将对最终组件精度控制产生显著效果。

(3) 装配精度几何量与工作性能物理量之间的关联关系。本文探讨了航空发动机实际运行工况之外的常温、常压条件下的转子装配精度控制问题，仅限于静态调试和装配几何量的控制。对于构建能够表达航空发动机关键零部件的装配精度几何量与服役性能物理量之间的关联关系还任重而道远。结构精量化设计方法对探索航空发动机系统“尺寸-精度-性能”之间的映射关系、发展面向装配和服役过程中装配精度可保持的数字化协调控制方法具有重要意义。