金属蠕变疲劳寿命预估模型研究进展

张力文，张小文，宋继萍

(1.西安航空职业技术学院，陕西 西安 710089； 2.洛阳双瑞特种装备有限公司，河南 洛阳 471000；3.中国试验飞行研究院，陕西 西安 710089)

常温下，设备的失效大部分以疲劳、腐蚀疲劳为主，但在电力、石化、核工业等部门，许多设备会长时间服役在高温高压环境下，如催化裂化用膨胀节管道、锅炉蒸汽管道、核反应堆的热端部件、化工容器和热工仪表、约束型膨胀节受力结构件等[1]。这些设备由于长时间在高温高压工况下运行，导致材料发生与常温设备不同的失效问题即蠕变断裂失效，常温设计是以材料的许用应力为设计准则，而在高温下，蠕变是必须要考虑的要素。并且在高温变载荷服役环境下，构件常常发生蠕变疲劳断裂失效。因此研究金属高温蠕变疲劳作用下的寿命预估对服役在高温下产品的安全运行具有重要的意义。本文综述了影响金属蠕变疲劳寿命的因素及蠕变疲劳寿命预测模型，并对高温蠕变疲劳寿命预估模型的建立进行了展望。

1 影响蠕变疲劳寿命的因素

蠕变疲劳引起的材料损伤不同于纯疲劳与纯蠕变造成的材料损伤，不仅包括纯蠕变与纯疲劳损伤，还包括蠕变疲劳交互作用对材料造成的损伤[2]。蠕变-疲劳损伤的影响因素很多，主要因素包括应力、保持时间、温度、加载、服役介质，还包括材料内部某些缺陷如点缺陷、面缺陷、线缺陷等。蠕变疲劳断裂方式主要包括穿晶断裂、沿晶断裂以及混合晶断裂，具体的断裂方式要基于材料宏微观分析才能做出判断[3]。影响蠕变疲劳失效寿命的关键因素有温度、应力水平、保载时间等方面。

1.1 温 度

温度对蠕变疲劳寿命的影响较大，它主要影响材料的机械力学性能，例如抗拉强度、屈服强度、断裂应变、蠕变强度等。温度较高时，材料蠕变疲劳寿命下降；这主要是由于温度较高时，原子扩散加剧，蠕变速率增大，晶界滑移易发生，容易在三叉晶界处产生微孔洞，微孔洞聚集产生微裂纹，在外力作用下，裂纹扩展直至发生断裂失效；反之，温度较低时，蠕变疲劳寿命会优于高温寿命。另外在一定温度区间内，某些材料在以应变控制方式进行蠕变疲劳试验时会发生动态应变时效它是在金属及合金中位错与溶质原子的交互作用所表现出来的一种强化效应，即变形与时效同时发生。因此高温下应使用抗蠕变疲劳性能好的耐热钢。

1.2 应力水平

蠕变疲劳试验加载控制模式可分为恒应力控制加载与恒应变控制加载。以应力控制模式加载时，应力峰值越大、应力幅越大，材料的蠕变疲劳寿命越小，这种情况下，疲劳对材料造成的损伤是主要因素。目前纯疲劳的寿命预估采用经典的S-N曲线，纯蠕变常采用Norton本构模型；蠕变-疲劳寿命模型的建立大多是基于材料的延性耗竭理论，这种寿命模型不但考虑了蠕变损伤、疲劳损伤，还考虑了两者交互时产生的损伤，其失效机理比纯疲劳、纯蠕变复杂的多。Zhang Xiancheng等[4]对304不锈钢进行了蠕变疲劳试验分析，结果表明，保载时间相同时，应变范围越大，蠕变疲劳循环周次越低。陈国良[5]等人对12Cr-1Mo-V钢进行大量研究，将蠕变曲线划分为疲劳区F、蠕变区C和蠕变疲劳区CF。在F区，疲劳损伤对材料寿命影响较大；在C区，蠕变损伤对材料寿命影响较大。而在CF区，不仅存在疲劳损伤和蠕变损伤，还包括蠕变-疲劳产生的交互作用引起的材料损伤，因而这一区域相比其他两区域材料寿命是最低。

1.3 保载时间

保载时间的长短和应力应变加载速率的大小同样影响着蠕变疲劳寿命。总的来说，保载时间越长，蠕变疲劳寿命越短。同时，拉伸保载蠕变疲劳寿命低于压缩保载蠕变疲劳寿命。郝玉龙[6]对P91钢蠕变疲劳分析证明了这一点。保载时间越长，材料断裂主要以蠕变沿晶断裂为主，反之，以疲劳穿晶断裂为主，也有混合断裂形式。一般来说，保载时间越长，对寿命的敏感性越大，但也有些合金如少数的高温合金、铜合金，在某一应变范围内，保载时间对蠕变疲劳寿命才会有显著影响。超过此范围时，保载时间对失效寿命的影响程度会降低。加载速率越大，蠕变疲劳寿命越短。

1.4 环境影响

金属蠕变试验及蠕变疲劳试验通常在空气中进行[7-8]，所以在高温下会出现氧化损伤，氧化损伤会与疲劳蠕变损伤综合加速材料的断裂。高温下有碳化物的析出，碳化物主要在晶界形成，导致晶界处脆化，在该处易萌生疲劳裂纹，并在外部应力作用下发生扩展在晶粒内产生孔洞，孔洞聚合导致有效承载面积减小，当内部应力超过强度极限时导致材料发生断裂失效。实际工作中的构件一般在具有腐蚀性的气体、液体中，而材料与腐蚀性介质通常会发生一定的物理或化学反应，如氢脆、腐蚀等，容易在材料内部某局部产生较大的应力集中而引起较差的机械力学性能。

2 蠕变疲劳寿命预估模型

连续介质损伤力学理论不仅描述材料的损伤行为，而且讨论宏观裂纹的形成过程，并从材料科学和连续介质力学的角度研究损伤变量的演化及其对材料寿命的影响[9]。金属材料内部往往存在着各种缺陷，包括点、线、面、体缺陷，这些缺陷往往是造成蠕变疲劳损伤的主要因素，例如蠕变孔洞常常在这些区域内形核，在拉伸应力下不断长大，聚合，最终导致材料发生失效断裂。目前，国内外学者采用损伤力学原理对蠕变损伤、蠕变疲劳损伤进行了大量研究，并基于宏观变形行为提出了许多预测材料在蠕变疲劳交互作用下寿命估算模型，这些模型为高温蠕变设计提供了理论依据。主要包括以下几种：

1)线性累积损伤法

Miner提出了高温疲劳线性累积损伤公式[10]：

对于常幅载荷

(1)

对于变幅载荷

(2)

式中：D为总损伤量；N为蠕变疲劳循环数；Ni为第i个幅值载荷下的纯疲劳循环数，次；Nf为不同幅值载荷下总的纯疲劳循环数，次；t为蠕变循环断裂时间，h;tR为常幅值载荷下纯蠕变断裂时间,h；ti为第i个幅值载何下纯蠕变断裂的时间，h；φc为纯蠕变损伤;φf为纯疲劳损伤。当φf+φc=1时，认为材料失效。

式(2)表明材料的疲劳与蠕变损伤是相互独立的，但蠕变疲劳交互作用引起的材料损伤并没有给予考虑，即并不是所有材料D都等于1，许多情况结果大于1或小于1。为了将蠕变疲劳交互作用引起的损伤予以考虑，Lagneberg[11]等人在此基础上提出增加两者的交互项来引入蠕变疲劳交互作用带来的损伤：

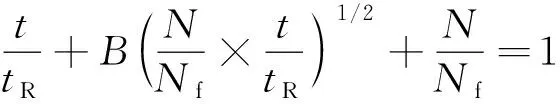
(3)

(4)

式中：A、B为交互作用系数。

线性累积损伤模型适用于应变控制的蠕变疲劳寿命预估。具有形式简单、物理意义明确的优点，但该模型未考虑各级载荷加载顺序对寿命的影响且未计及材料发生的循环加工硬化行为。此外，该模型需要进行纯蠕变和纯疲劳试验，因此试验周期较长且寿命预测精度较低。

2)延性耗损法

延性耗损理论认为蠕变、疲劳对材料造成的损伤并不是独立的，而是相互影响的，也就是说蠕变和疲劳不仅各自对材料造成损伤，还产生交互作用加大了高温下对材料的损伤程度[12]。达到某一临界值时会导致材料断裂失效，其寿命估算式为

(5)

式中：Δεcr为蠕变应变增量；Dc为总蠕变量；Nc为循环周次。

该方法比较适合蠕变和疲劳之一为主导的失效形式，蠕变疲劳交互作用带来的材料损伤并没计及，为了计及两者交互损伤，郝玉龙[13]提出以下具有保载时间的蠕变寿命模型

(6)

(7)

εA=f(tH)

(8)

(9)

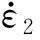
延性耗损法是基于黏性流、应变速率及应变控制模式的概念建立起来的，只适用于应变控制且以塑性应变为主导的Cr-Mo钢高温蠕变疲劳寿命的预估。该模型形式简单且物理推导严密、寿命预测精度较高。缺点是需要已知保载时间、稳态蠕变速率及寿命。

3)Manson-coffin方程

1954年Manson和Coffin等[14-15]在大量试验的基本上提出了预测高温低周疲劳寿命的关系式：

(10)

式中:Δεp为塑性应变范围；Nf为失效循环数，次；β和C1为材料常数。

常温下β取0.5，C1与真实拉伸断裂应力相关，一般情况下C1≈εf，εf为真实断裂应变，在给定的断裂应变和塑性应变范围以及β条件下，即可确定材料的低周循环寿命。Manson-Coffin模型适用于应力控制模型下的低周疲劳，该模型未考虑蠕变损伤对寿命的影响，且未考虑蠕变和疲劳的交互作用，因此寿命预测精度偏低。

4)基于平均应变速率的寿命预测模型

平均应变速率法的基本思想是延性耗竭理论[16]，该理论认为，应力控制下的蠕变疲劳损伤包括静蠕变损伤、动蠕变即循环蠕变损伤和蠕变疲劳交互作用下引起的材料内部损伤，当所有损伤导致材料延性消耗完时就会发生断裂失效。断裂失效准则为εmax≈εm=εf。其中εmax表示循环累积最大应变、εm表示循环累积平均应变、εf为断裂延性，寿命关系如下：

(11)

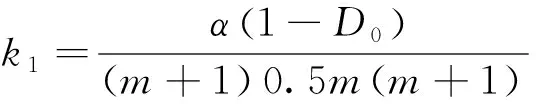
(12)

式(1)可简化为

(13)

平均应变速率模型适用于应力控制模式下的高温或低温疲劳寿命预测，且使用半寿命处的平均应变速率代替最小蠕变速率时，该模型可预测纯蠕变寿命预估。此外，该模型将加载条件对高温循环寿命的复杂影响转变为简单的线性表达式，具有未知参数少、形式简单、预测寿命精度高等优点，但其缺点是需要得到半寿命处的平均应变速率。

5)基于延性耗竭的寿命预测模型

该理论认为，材料在高温变载工况条件下是以黏性流方式产生蠕变疲劳损伤，晶界延性损伤是由蠕变主导，晶内延性损伤是由疲劳主导，蠕变与疲劳两者之间的相互作用对材料的损伤产生了不可忽略的促进作用，当达到材料的断裂延性值时就会发生断裂失效[17]。其断裂失效准则表达式为 ∑νd=Tm，其中试验循环加载时间与材料所受的拉伸应力之间的乘积表示动黏性νd，材料循环强度与延性之间的乘积表示材料的韧性Tm。最终推导的蠕变疲劳寿命的表达式如下：

(14)

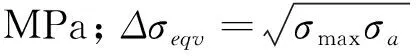
延性耗竭模型综合考虑了加载速率、保载时间、平均应变速率和应力比对寿命预测的影响，该模型适用于应力控制模型下的寿命预估，且寿命预测精度高。缺点是需要采集的试验数据较多，主要包括半寿命处的平均应变速率、加载速率和保载时间。

6)频率修正法与频率分离法

Coffin[18]在Eckel 和Cole提出的“频率—时间”的基础上提出了频率修正法，从而将载荷保持时间引入到蠕变疲劳寿命预估模型中，推导出的公式可表示如下：

(15)

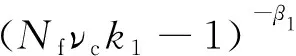
(16)

对于加载波形对蠕变损伤产生一定影响的材料，频率可定义为

(17)

式中：tcy为蠕变疲劳循环时间，s；tt为拉伸载荷保持时间,s；tc为压缩载荷保持时间,s。

对于平均应力较大的，Ostergren[19]等人将损伤函数引入到蠕变疲劳寿命模型中：

(18)

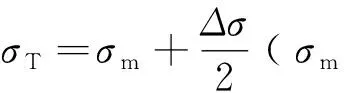
Leven[20]对Cr-Mo-V转子钢进行了具有保载时间的应变控制试验，提出了540的频率修正公式：

(19)

在频率修正法基础上，1976年Coffin[21]在考虑了拉伸载荷保持频率νt=1/tt和压缩载荷保持频率νc=1/tc的基础上提出了频率分离法，通过该方法对Coffin-Manson进行了修正，修正后的Coffin-Manson公式为

(20)

式中：Δεin为非弹性应变(塑性应变和蠕变应变之和)。

频率修正法和频率分离法通过引入频率变量建立了考虑保载时间的蠕变疲劳寿命预估模型，适用于具有拉压保载的工况条件，间接地反映了材料在高温下的蠕变-疲劳交互作用对失效寿命的影响，但由于该模型忽略了压缩保载对微裂纹的闭合作用，因此在蠕变疲劳寿命预测精度上偏低。

7)基于能量守恒的蠕变疲劳交互寿命模型

浙江大学陈凌[22]根据能量守恒定律和动量守恒定律，提出了一种新的蠕变―疲劳寿命预测模型。该模型表达式如下：

(21)

为方便数学计算，将函数g定义为power指数函数，上式改写为

(22)

(23)

式中：η为内能转化比；ΔE为试样内部能量从初始状态到最终失效状态的变化，J；Δei为每一循环的内能改变量，J；ΔWti为每一循环的总应变能，J；α，m为常数。

基于能量守恒的蠕变疲劳寿命预测模型是基于热力学定律推导出来的，具有一定的理论支撑，且寿命预测精度高。该模型在理论推导过程中未涉及循环控制模式，因此适用于应力控制或应变控制下的蠕变疲劳寿命预测，其缺点是需要得到半寿命处的非弹性应变能及应变范围。

8)延性耗竭与损伤力学寿命预估模型

陈凌[23]等在损伤力学和延性耗竭理论的基础上，建立了新的适用于工程的高温蠕变疲劳寿命预估模型。该模型将蠕变疲劳交互作用下的延性耗竭循环周次与断裂失效寿命建立了对应关系，表达式如下：

εm=a+b(N/Nf)c

(24)

(25)

式中：εm为N对应的平均应变；N为某一时刻循环数；Nf为失效寿命。

延性耗竭与损伤力学寿命预估模型适用于恒温加载条件下寿命出现波动的情况，该寿命预测模型较为简单，且具有一定的理论依据，适合应用于实际工程。

4 展 望

综上所述，目前现有的预测材料高温蠕变疲劳寿命的模型大多是依据试验表现出的宏观现象分析得到，并未考虑微观组织演化对寿命的影响。例如，对于一些沉淀强化铝合金，合金在较高温度下发生蠕变变形的同时，还会出现时效强化现象，而时效过程产生的析出相对于蠕变变形起到阻碍作用，蠕变变形产生的位错促进沉淀相的析出过程，蠕变变形和时效强化存在强烈的交互作用[24]。因此上述蠕变疲劳模型不能反映出沉淀相对材料蠕变疲劳寿命的影响。未来的研究方向是建立基于宏微观耦合作用的蠕变疲劳失效寿命预估模型，探索金属及合金材料在不同温度、时间和应力下的蠕变疲劳损伤机理，从而建立应力、时间以及温度之间的三维响应图，预测给定温度、时间、应力的蠕变疲劳寿命。

5 结 语

本文综述了影响金属材料高温蠕变疲劳失效寿命的因素以及现有的高温蠕变疲劳交互作用下的失效寿命预估模型，并分析了各模型的适用范围及优缺点。通过以上分析可知，蠕变疲劳寿命受多种因素的影响，现有的蠕变疲劳寿命预测模型是在不同试验条件下所获得的试验结果的基础上建立的，因此各个模型具有一定的局限性。另外，现有的模型只关注了材料的宏观表现，未考虑材料微观组织演化对寿命的影响，并且不同材料、不同工况下的蠕变疲劳之间交互作用存在差异，导致模型适应性较低。未来应探索出基于物理机制的宏微观耦合蠕变疲劳交互作用下的寿命预测模型。