基于双向位图的CSR大规模图存储优化
甘新标 谭 雯 刘 杰
(国防科技大学计算机学院 长沙 430017)
(xinbiaogan@nudt.edu.cn)
大数据时代,超级计算机系统结构面临着巨大的机遇和全新的挑战.图搜索处理对计算机系统存储和带宽要求甚高,传统的超级计算机系统处理大规模图数据的效率低下.Graph500作为数据密集型计算机系统的评测基准,能够准确反映E级计算机系统的大数据处理能力和指导E级计算机系统设计.
Graph500以每秒遍历的边数(traversed edges per second, TEPS)为性能指标来衡量超级计算机处理数据密集型应用的能力.Graph500测试性能主要受限于图测试规模和访存带宽,尤其是内存空间大小直接决定了图的测试规模.因此,本文提出了基于双向位图的大规模图数据压缩存储方法(bidirectional-bitmap based compressed sparse row, Bi-CSR)以增加Graph500图测试规模,并提升Graph500图测试性能.
本文的主要贡献有2个方面:
1) 提出了基于双向位图的稀疏矩阵压缩存储方法Bi-CSR,大幅减少了大规模图存储空间.
2) 将Bi-CSR应用于天河E级验证的Graph500测试,达到了良好的测试性能.
1 相关工作
很多现实问题可以抽象为图形结构,因此,图形理论在众多学科中应用广泛[1-3].从现实问题中抽象出来的图形结构通常具有2个特点:小世界性(small-world)[4]和无尺度性(scale-free)[5].
图遍历是大数据时代背景下的一种典型的数据密集型应用,Graph500测试基准是典型的数据密集型程序.其核心搜索程序能够适用于数据密集型应用,能够解决真实世界中的实际搜索问题,测试数据集能够反映真实数据集的普遍特征,并且Graph500具有较差的时间和空间局部性,因此,Graph500具有一般大数据问题的主要特征.近年来,面向Graph500核心算法BFS的优化遍历取得了一系列重要的进展.
Bader等人[6]在Cray MTA-2多结点上实现了多线程的并行BFS算法,利用硬件多线程技术来隐藏访存延迟,取得了很好的性能提升;Agarwal等人[7]提出利用位图的数据结构来表示算法中的visit结构,增加了visit的局部性,减少了访存的次数;Beamer等人[8]开创性地提出了一种Top-down与Bottom-up相结合的混合算法,所实现的混合算法能够有效地减少搜索过程中遍历的边数,减小了访存开销,极大地提高了程序的性能;Ueno等人[9]面向极大规模并行与分布式机器提出了一种高效的BFS算法,并应用于“京”超级计算机系统,达到了的良好测试性能;清华大学林恒等人[10-11]面向“神威太湖之光”实现了一种可扩展的BFS算法,实现了模块流水映射、无竞争的数据混洗、基于组消息的批处理等关键技术,在神威太湖之光超级计算机全系统上获得了23755.7GTEPS的测试性能[11],上述优化技术和方法本质上都属于加速图遍历来提升Graph500测试性能.图遍历速度是Graph500测试性能的重要影响因素,工程实践表明:Graph500测试性能直接受限于图测试规模.分析Graph500榜单可知,测试图规模越大,Graph500性能越高.内存空间大小直接决定了Graph500图的测试规模,Graph500的 Kronecke生成器生成的图形通常用邻接矩阵表示,由于顶点的平均度数较低,其邻接矩阵为稀疏矩阵,因此,图形的邻接矩阵存储格式直接影响了Graph500图测试规模.
典型的稀疏矩阵存储格式有COO(coordinate),DIA(diagonal)[12],CSR(compressed sparse row), CSB(compressed sparse block),ELL(ELLPACK)和HYB(hybrid ELL+COO)等[13],上述压缩格式在天河验证系统512个结点上的最大图测试规模及性能如图1所示,纵轴采取GTEPS为性能指标.
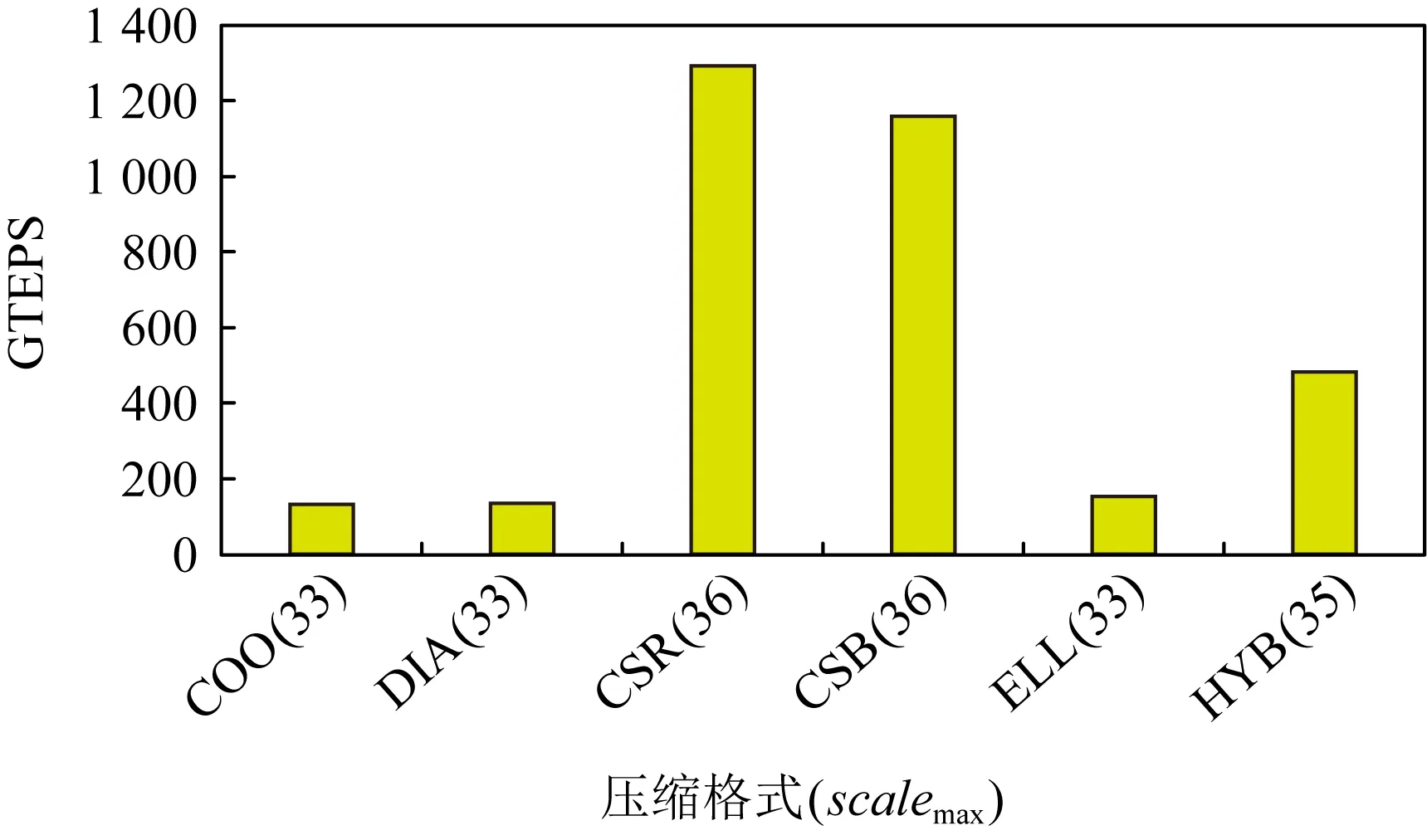
Fig. 1 Various format testing on available max scale with GTEPS comparison图1 不同格式的最大测试图规模及性能比较
由图1可知,CSR格式在天河验证系统上的最大图测试规模为scalemax=36,稳定测试性能为1310GTEPS.各数据压缩方法除了压缩效率和最大图测试规模及性能的不同,各种数据压缩方法操作性、灵活性、可扩展性以及适用领域方面也存在明显的差异,其中,DIA和ELL格式在进行稀疏矩阵矢量乘积时效率最高,它们是应用迭代法求解稀疏线性系统最快的格式[12];CSB的优势是易于向量并行;ELL的优点是快速,COO的特点是灵活,二者结合后的HYB格式是一种优良的稀疏矩阵表示[13-14];CSR相比COO,HYB,CSB,DIA,ELL,更加灵活,易于操作[13];因此,Graph500参考实现中采用了CSR存储Kronecker生成图.CSR可以采用数组或位图2种数据结构来完成图压缩存储,基于数组结构的CSR图存储与基于单向位图结构的CSR图存储空间利用率十分有限[9-11],为此,本文提出了基于双向位图的CSR大规模图存储优化方法进一步提高Graph500图压缩存储效率,最大化Graph500图测试规模和提升Graph500测试性能.

Fig. 2 Presentation with adjacency matrix storage for graph图2 图的邻接矩阵表示
2 Graph500
Graph500以每秒遍历边数TEPS为性能(per-formance)指标来衡量超级计算机处理数据密集型应用的能力.TEPS要由图的规模和图形遍历的时间共同决定,尤其是内存空间大小直接决定了图的测试规模.
2.1 基本流程
Graph500基本流程包括图生成、图构造与存储、图遍历以及图验证4个主要步骤[15-16],Graph500图生成采用了Kronecker生成器,生成的图满足小世界性与无尺度性[15].Graph 500图形生成器有2个输入参数,分别是图形规模scale和边因子edgefactor.
假定scale=n,edgefactor=m,则生成的图具有2n点和m×2n条无向边[15].
Graph500中仅包含了2个计时模块:图存储变换和图遍历,并且图遍历占据其中绝大部分时间,假定Graph500的搜索时间为t,则对于scale=n,edgefactor=m的图,Pteps为性能指标,Pteps=m×2nt.
图存储将生成的图信息转换为包含顶点、边以及联系的元组信息列表,通常以邻接矩阵的形式高效存储.Pteps由图规模和搜索时间共同决定,并且图的规模对Pteps的影响尤为关键,图结构的存储和表示模式是影响Graph500图测试规模的重要因素.
2.2 图结构的存储与表示
图G(V,E) 包含顶点集合V和边集合E.通常对图形的顶点进行编号,使用vi表示图中编号为i的顶点,使用顶点对(vi,vj)表示顶点vi到顶点vj的边.对于无向图的每条边,可以看作2条有向边.
Graph500生成图形通常采用邻接矩阵A表示,其中的每一行Ai为邻接表,图的邻接矩阵表示如图2所示.
邻接矩阵中第i行、第j列的元素Aij表示边(vi,vj).对于无权图,仅需要说明边是否存在,通常使用1 表示存在这样的边,0 表示不存在这样的边.
大部分从现实问题抽象出来的图,如Kronecker图生成器生成的图,顶点的平均度数远小于顶点总数,并且符合6度分离原则和小世界效应[4-5],其邻接矩阵通常为稀疏矩阵[12,18-20],因此,Graph500中采用了基于CSR的稀疏矩阵存储方法,CSR包含2个数组:columns和rowstarts.数组columns存储按行压缩的列标号,数组rowstarts存储对应行在columns中的索引位置,如图3(a)所示.

Fig. 3 Structureof CSR storage for graph图3 图的CSR存储结构
如图3(b)所示,columns中的标号为邻接矩阵A对应非零元素的列标号,第1个数字4表示第1个非零元的列标号为4,第2个数字5表示第2个非零元的列标号为5,第3个数字3表示第3个非零元的列标号为3,第4个数字1表示第4个非零元的列标号为1.rowstarts中的索引位置对应A中非零元的行标号相对偏移,即对应行中非零元的个数,如:第2个数字2和第1个数字0表示A中第0行中非零元的个数为2-0=2,第3个数字2和第2个数字2表示A中第1行中非零元的个数为2-2=0,第4个数字2和第3个数字2表示A中第2行中非零元的个数为2-2=0.
Graph500生成无向图的邻接矩阵表示总是对称的,采用CSR图数据存储.CSR作为通用的稀疏矩阵存储方法,具有存储模式灵活、易于操作等诸多优势, 但是,CSR的大规模图存储效率与天河E级验证系统的小内存体系结构特征并不能完美适配,这是因为Graph500的测试性能主要受限于访存带宽和内存规模,当系统内存超过阈值后(即输入图规模达到一定规模),访存带宽将激变成为性能瓶颈,基于天河E级验证系统的规模和配置,访存带宽尚未成为性能瓶颈,天河E级验证系统的Graph500测试性能主要受限于内存大小.面向天河E级验证系统的Graph500优化设计应当充分发挥验证系统优势,最小化天河E级验证系统小内存的局限性,设计与验证系统的规模与存储层次相适应的图数据压缩方法,准确度量天河E级验证系统的大数据处理能力,因此,面向天河E级验证系统提出了一种基于双向位图的稀疏矩阵压缩大规模图存储方法Bi-CSR,以最大化Graph500图测试规模和提升Graph500测试性能.
3 基于双向位图的稀疏矩阵压缩存储方法
针对天河E级验证系统小内存的特征,提出了与天河E级验证系统的小内存匹配的基于双向位图的大规模图数据压缩存储方法Bi-CSR.Bi-CSR在CSR存储结构的基础上仅保留存储一个或者多个顶点或边的起始位置来压缩CSR的数据结构,并且在行列2个方向分别引入位图(bitmap)来辅助识别顶点和边信息,其中行位图中每一位存储一个顶点信息,列位图中每一位存储连续列编号信息.
3.1 基于行方向位图的稀疏矩阵压缩
基于行方向位图的稀疏矩阵压缩主要目的是减少大规模图存储空间,扩大Graph500图测试规模和减少访存次数.基于行方向位图的CSR存储通过引入行方向位图数组row_bitmap,并且,将CSR存储结构中的数组rowstarts采用改进的行数组CSR_rowstarts′和位图数组row_bitmap来表示,如图4(b)所示.将数组rowstarts中零元行标号索引采用1 b来表示数组rowstarts中使用1个整型(32 b)来表示的索引信息,最大限度压缩了数据存储空间.位图数组row_bitmap中的每一位对应所在的行是否有非零元.图规模越大,图的稀疏特征表现越明显,越多的采用整型(32 b)表示的索引信息可以使用1 b来辅助标注,最大限度节约了图数据的存储空间.
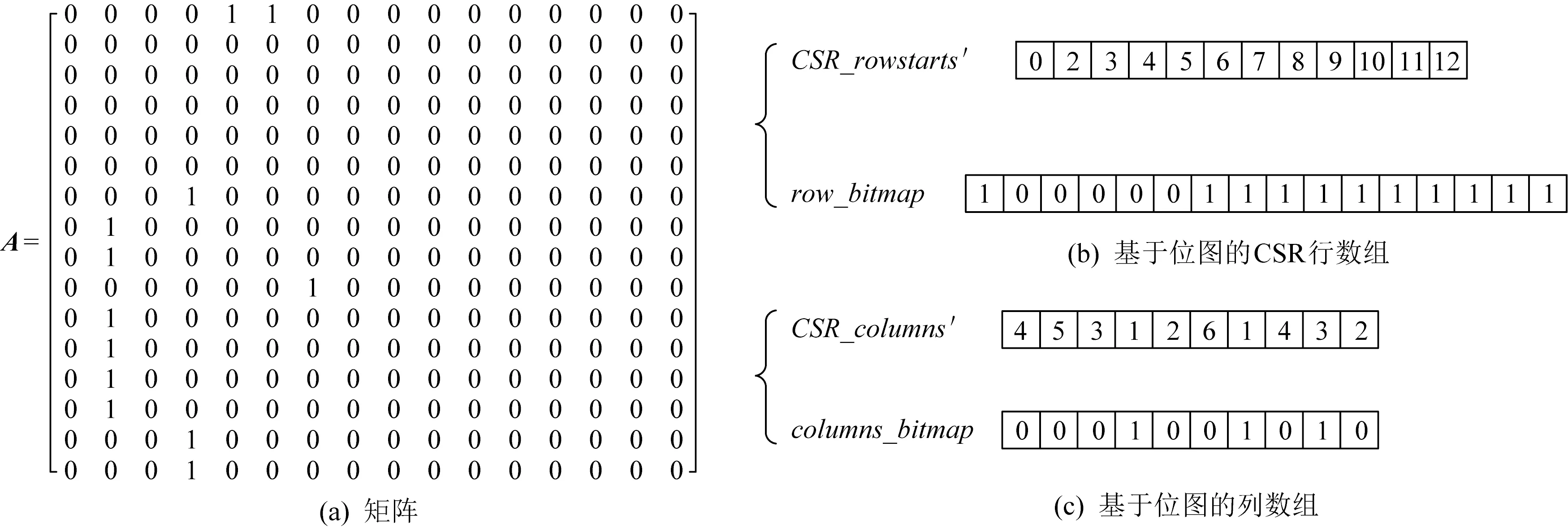
Fig. 4 Structure on Bi-CSR storage for graph图4 Bi-CSR压缩存储结构
3.2 基于列方向位图的稀疏矩阵压缩
基于列方向位图的稀疏矩阵压缩主要目的包括进一步减少大规模图存储空间,最大限度扩大Graph500图测试规模和减少访存次数,以及为面向天河E级系统的可变宽度向量化开辟优化空间.
基于列方向位图的CSR存储通过引入列方向位图数组columns_bitmap,并且,将CSR存储结构中的数组columns采用改进的列数组CSR_columns′和位图数组columns_bitmap来表示,如图4(c)所示.为了更加清晰地描述数组columns_bitmap中的含义,作定义:
定义1.列连续片段.列方向上连续出现非零元,连续片段的长度len≥2.
定义2.列非连续片段.列方向上未连续出现非零元,列非连续片段的长度len=1.
定义3.紧前位(closely front bit, CFB).位图数组与当前位紧邻的前一位,记为BCF.
定义4.紧前缺位(non-closely front bit, non- CFB).位图数组中的首位没有紧前位,即为紧前缺位,记为non_BCF.
columns_bitmap中的每一位对应所在的列编号是否为连续列编号片段的起始列编号,准确含义:
数组columns中的每一位对应列连续片段fragment的起始列编号column_label,或是列连续片段的长度值len≥2,或是列非连续片段non_fragment的列编号column_label,具体含义应结合数组columns_bitmap中对应位标识来判定;columns_bitmap中的每一位对应数组CSR_columns′中相同偏移的元素值是否为连续列编号片段的起始列编号column_label,1表示CSR_columns′中相同偏移的元素值为列连续片段的列编号,0表示为非连续片段non_fragment的列编号或是连续片段长度的标识.若0的紧前缺位non_BCF是0则表示CSR_columns′中相同偏移的元素值为非连续片段的列编号column_label,若0的紧前位BCF是1则表示columns′中相同偏移的元素值为连续片段的长度值,若0的紧前位BCF是0,则表示columns′中相同偏移的元素值为非连续片段non_fragment,列编号column_label.例如:由于紧前缺位non_BCF,columns_bitmap第1个数字0,表示对应columns′中第1个数字4为第1个非零元的列编号;由于紧前位BCF为0,第2个数字0表示对应CSR_columns′中第2个数字5为第2个非零元的列编号;第4个数字1表示连续片段的起始列标号为CSR_columns′中第4个数字1,即第4个非零元的列编号为1;由于CFB第4个数字是1,第5个数字0表示连续片段的长度,其长度值为CSR_columns′中第5个数字2.
4 实验与性能分析
为了验证系统的大规模图存储优化方法Bi-CSR,将Bi-CSR应用于天河E级验证系统进行Graph500工程测试.
4.1 天河E级验证系统
天河E级验证系统主要包括计算处理分系统、高速互连分系统、并行存储分系统、服务处理分系统、监控诊断分系统和基础架构分系统等,如图5所示.面向天河E级验证系统的Graph500重点关注其中的计算处理分系统和并行存储分系统.
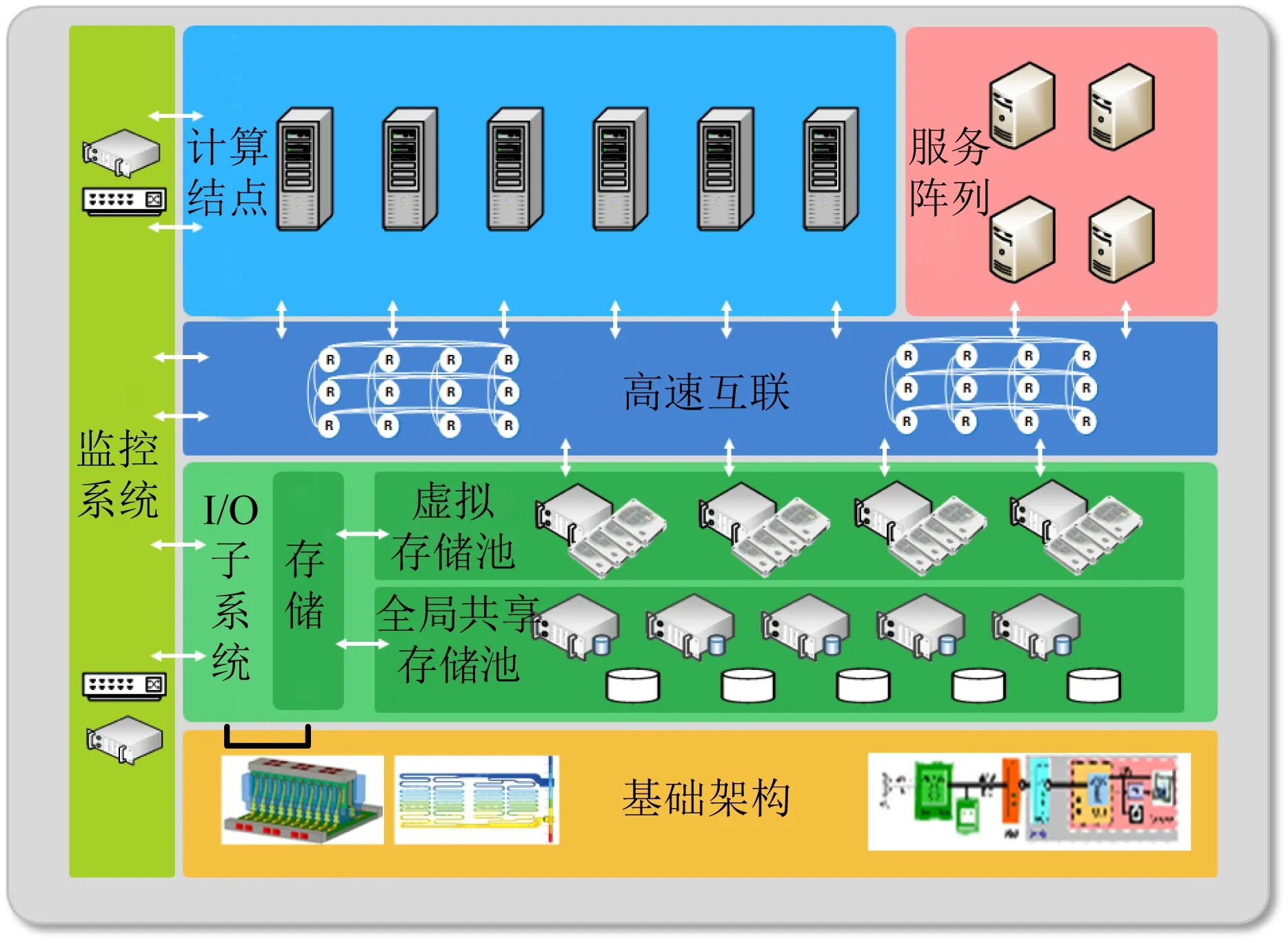
Fig. 5 Architecture for Tianhe pre-exascale system图5 天河E级验证系统结构图
计算处理分系统由512个计算结点构成,是系统主机的计算核心.每个计算结点包括3颗Matrix-2000+微处理器,运行频率为2.0 GHz,峰值性能为6TFLOPS.
并行存储分系统采用超高并发度的多层面并行存储架构;全局共享存储层包含20个IO存储结点,每个存储结点集成64 TB磁盘阵列,提供共享存储总容量1.28 PB.配置2个IO管理结点和1套8 TB全闪存阵列存储管理元数据,提高元数据IO吞吐率.E级验证系统并行存储分系统的具体配置包括:32个IO加速结点、20个IO存储结点、2个IO管理结点和1套全闪存阵列,总存储容量1.28 PB.
4.2 实验配置
为了验证天河E级原型系统的数据密集型应用处理能力,本文将Bi-CSR应用于Graph500测试中,形成了面向天河E级验证系统的Graph500测试版本THE-G500(Tianhe exascale Graph500).
为了验证Bi-CSR的有效性,我们在天河E级验证系统上分别采用标准参考版本Graph500和面向天河E级验证系统的THE-G500版本进行了详细的测试与比较分析,实验平台为部署于天津超算的天河E级原型系统,与Graph500测试密切面相关的系统参数如表1所示:

Table 1 Configuration for Testing Graph500
4.3 Bi-CSR存储空间分析与性能开销验证
Bi-CSR图数据进一步压缩的基本思想为大规模图矩阵的CSR压缩存储中每行或每列中出现多个非零元,然后利用行列双向位图协作行列标号和位移的计算,即将32 b标识的列标号和位移改进为1 b的位图索引.
理论上,每个非零元减少的存储空间为
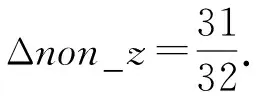
(2)
由于Graph500的Kronecker图生成器生成的图符合小世界性和6度分离理论,应用到Graph500图的CSR存储结构中,可以推断出图的稀疏矩阵中每行出现至少2个非零元的概率为
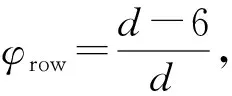
(3)
其中,d为CSR图结构中每个顶点的平均度数.
由于装备天河E级验证系统的众核处理器支持可变宽度向量并行,因此,基于列方向位图的CSR压缩由出现非零元片段的概率可以松弛为每列出现多个非零元的概率:
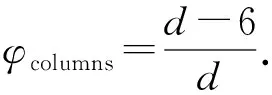
(4)
因此,仅应用基于行方向位图的Bi-CSR的图数据存储空间减少量:
Δrow=Δnon_z×φrow.
(5)
仅应用基于列方向位图的Bi-CSR的图数据存储空间减少量:
Δcolumns=Δnon_z×φcolumns.
(6)
综上所述,基于行列2个方向位图的Bi-CSR的图数据存储空间减少量为
Δspace=1-(1-Δrow)×(1-Δcolumns).
(7)
实际应用的Bi-CSR图数据压缩中,由于Graph500中顶点平均度数d=16,测试中不同图规模以16×32的拓扑结构分布于E级验证系统上,每个结点存储空间减少量如表2所示:
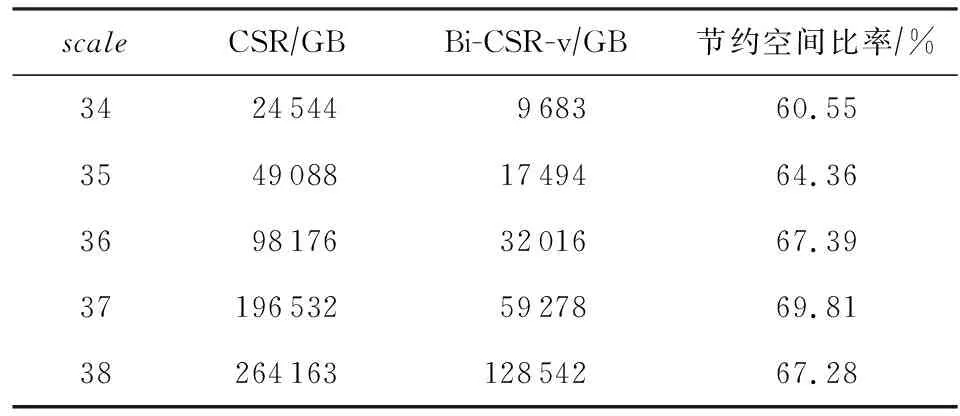
Table 2 Space Save Comparison Between Bi-CSR and CSR表2 基于Bi-CSR的图数据空间节约率
由表2可知,THE-G500在天河E级验证系统的测试过程中,应用Bi-CSR方法后大规模图数据存储空间的节约率与式(5)~(7)表征的理论存储空间节约率基本吻合,在scale=34时,大规模图存储空间节约率超过了60%,当scale=37时的空间节约效率达到最大值,接近70%.
Bi-CSR较CSR方法,存储效率提升明显,但是,Bi-CSR需要增加行方向位图数组row_bitmap和列方向位图数组columns_bitmap,增加了额外的存储空间来获得更高的压缩比;并且Bi-CSR较CSR计算复杂度更高,需要引入紧前位BCF、紧前缺位non_BCF对列非零元片段是否连续进行判定与索引,增加了3%~5%的时间开销,Bi-CSR性能开销测试验证如图6所示:
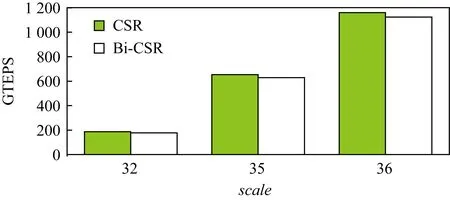
Fig. 6 GTEPS comparison between CSR and Bi-CSR with the same testing scale图6 相同图测试规模下的CSR与Bi-CSR性能比较
由图6可知,相同输入图测试规模下,CSR的测试性能是略优于Bi-CSR的,实验数据表明:相同图测试规模下,Bi-CSR约有3%~5%的性能损失,但随着图测试规模的增大,性能损失逐渐缩小.Bi-CSR具有更高的图稀疏矩阵的存储压缩比,相同内存下能够测试的图规模也更大,因此能够显著提升Graph500测试性能.因此,Bi-CSR引入了行列位图数组和更高的计算复杂度,但是获得了更高的图存储压缩比,相同内存规模下能够完成更大的图规模测试,Graph500测试性能更优.
4.4 Graph500性能测试与分析
装备天河E级验证系统的MT-2000+为通用众核处理器.不同稀疏图压缩方法的性能测试比较如图1所示,本节的重点是关注CSR与Bi-CSR的性能比较分析,因此,对不同图规模和运行配置下对基于CSR的Graph500和基于Bi-CSR的THE-G500性能进行了详细的测试分析与比较,如图7所示.
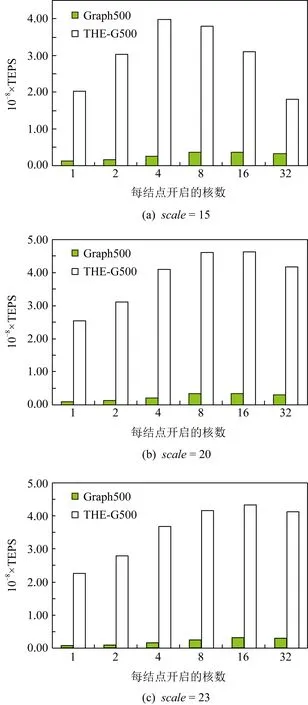
Fig. 7 TEPS comparison on different running threadscores per node图7 不同线程并行时程序性能比较
由图7可知,在天河E级验证系统上,参考版本Graph500程序和天河E级验证系统版本的THE-G500具备在实际测试过程中(scale>15)每结点开启16线程并行时,性能整体表现最佳,并且图的测试规模越大THE-G500性能加速效果越明显.当测试规模为scale=15,开启2个线程并行时,THE-G500性能提升最大,约19.35倍,开启32个线程并行时,THE-G500性能提升最小,约5.49倍,该规模下THE-G500平均性能提升约12.9倍;当图的测试规模为scale=20,仅开启1个线程,THE-G500性能提升最大,约26.79倍,开启32个线程并行时,THE-G500性能提升最小,约13.33倍,该规模下THE-G500平均性能提升约18.31倍;当图的测试规模为scale=23,开启2个线程并行时,THE-G500性能提升最大,约37.88倍,开启32个线程并行时,THE-G500性能提升最小,约13.98倍,这是因为本地存储单元有限,线程增加了,可利用局部存储空间少了,数据迁移至更远的外部存储空间,该规模下THE-G500平均性能提升约23.99倍.
应用Bi-CSR大规模图空间压缩方法、面向MT-2000+天河E级验证系统版本的THE-G500全系统性能测试如图8所示,图8中表现的性能均为在对应结点规模下能够稳定测试的最大图规模scale值.

Fig. 8 Performance for THE-G500 testing on tianhe pre-exascale system图8 面向天河E级验证系统的THE-G500性能测试
由图8可知,面向E级验证系统版本的THE-G500性能较官方的参考Graph500测试程序性能提升显著,单结点最小加速比接近20倍加速比,全系统最大加速超过100倍,受限于系统内存,当图规模测试到scale=36,参考版本Graph500不能稳定地完成测试任务,最可能原因是内存压力大,对网络以及系统稳定性要求高.由于Bi-CSR能够节约近70%的存储空间,THE-G500在全系统下可以将图的测试规模成功进一步扩大到scale=37,稳定测试性能为2.131E+12TEPS,当图规模继续增大时,THE-G500也无法完成稳定测试,最重要的原因是,压缩优化后的图存储空间仍然超过了E级验证系统最大存储空间.综上所述,THE-G500较Graph500能够应用更大规模的图测试,并且,在相同可用存储空间下,THE-G500较Graph500的最大性能加速比已超过100倍,THE-G500性能加速比随着结点规模的增加具有更好的扩展性.需要说明的是,全系统THE-G500测试性能包含了可变宽度向量优化带来的性能提升,由于可变宽度向量优化是基于列方向位图的稀疏矩阵压缩方法的延伸,并且,可变宽度向量优化加速BFS遍历并不是本文关注的重点.因此,将可变宽度向量优化直接归入了基于列方向位图的稀疏矩阵压缩带来的性能提升.
面向天河E级验证系统,应用Bi-CSR方法设计实现了面向目标系统的Graph500测试版本THE-G500,实验结果表明:THE-G500能够充分发挥天河E级验证系统的数据密集型应用处理潜力,同时验证了面向天河E级验证系统的大规模图存储优化方法Bi-CSR的高效性.
5 总 结
E级验证系统将面向大科学工程计算,兼顾海量信息大数据智能处理平台,大规模图处理是评测超E级系统处理数据密集型应用能力的重要手段.为此, 针对天河E级验证系统小内存,基于CSR图结构引入行列双向位图进一步压缩稀疏矩阵存储空间,提出了大规模图数据压缩存储方法Bi-CSR,该方法将大幅减少稀疏矩阵存储空间,最大化Graph500图测试规模和提升Graph500测试性能,在天河E级验证系统512结点系统上,全系统稳定测试性能TEPS为2.131×1012, 面向天河E级验证系统时,位列Graph500 排名第9,同等系统规模下THE-G500性能表现优异.
贡献声明:作者甘新标提出了基于双向位图的大规模图存储压缩方法,并完成算法设计;作者谭雯参与算法编码实现、实验测试和论文修改工作;作者刘杰参与实验设计与讨论,制定实验内容,协调实验资源.

