制动夹钳单元静强度验证与确认

赵金良 孟永帅 刘 超

(中车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011)

有限元仿真分析技术正在不断快速发展，广泛应用于实际工程的设计当中。例如在汽车、船舶、飞行器、甚至是在日常使用的消费品当中[1]。因其具有建模时间短、成本低、能够缩短研发时间的优点，有限元分析在机械产品设计过程当中的作用越来越重要。但是，不同的有限元建模方案会导致不同的有限元仿真结果，而结果的准确性直接代表了有限元仿真建模方案的可行性。因此有限元仿真结果的准确性是工程设计和分析人员以及决策者最为关心的问题。如何评估与确定仿真结果的准确性成为仿真工作最为重要的环节之一。

ASME V&V是针对无全系统试验结果时的数值模拟准确性进行的严格量化的研究[2]，其目标就是对模型的仿真与试验的准确性进行验证与确认，使其模型的准确性有足够的理论依据和保证。

本文以某型号制动夹钳单元的静强度分析为研究对象，基于ASME V&V标准，确定该型号制动夹钳单元有限元模型的验证与确认方案，并评估该模型有限元仿真结果的准确性。

1 ASME V&V标准

ASME V&V标准是由美国机械工程协会(The American National Standards)制定。其标准主要包含两个部分：验证(Verification)和确认(Validation)；验证是评估计算模型是否精确地反映了数学模型的过程，确认是从模型使用程度的角度评估了模型是否精确反映了真实情况的过程[3]。

ASME V&V需要给出一种置信度，这个置信度是用来解决复杂问题的从计算得到的结果。但是，与其他标准不同，V&V标准并没有给出确定的每个步骤的具体操作规则，而是给出了一种处理问题的观念和想法，它是灵活的[3]。因此，对于验证与确认的方法，要研究适合该型号制动夹钳的确切方案。

2 验证与确认方案

2.1 验证方案[4]

ASME V&V给出了一套参考的评价方法，因为ASME V&V有限元验证方案只适用于受拉伸载荷的情况，对于受弯矩或者扭矩载荷的情况，并不具备验证能力。因此，本文选用J.R.Beisheim给出的验证方案[4]，具体如下：

利用公式

hm=hm-1/λ

Nm=λ3Nm-1

其中：公式中需满足m≥2；hm为变量m的网格尺寸，Nm为变量m的网格中的有限元单元数，λ为有限元细化比例常数。

而对于一个特定物体，通过有限元应力计算结果，得到相应的应力误差，从而评估有限元网格的误差：

Δσm=σm-σm-1

em=σ-σm

其中：σ为真实应力值，σm为变量m的应力值，em为应力值误差，εm为有限元验证因子。

因为真实应力值σ很难得到，因此通过有限元迭代法去估计真实应力值的大小，并应用以下公式：

最终百分比误差计算公式为：

评估其是否符合标准要求。

2.2 确认方案[5]

确认方案采用了ASME V&V给出的确认评价方案。

其原理是通过建立模型与试验的分布函数的积分，计算出因误差而导致的积分差面积，通过其面积指标给出仿真与试验确认的准确性指标。其积分函数如图1所示。

图1 分布函数及面积指标

仿真模型的正态分布概率积分为

试验数据的正态分布概率积分为

根据上述两个式子得到面积指标为：

其中，Sexp为试验采集数据的平均值。

其面积指标标准要求需要小于10%。

3 制动夹钳单元建模与验证

分析某型制动夹钳单元的结构特点，并根据其结构特性，利用商业有限元软件建模。

3.1 制动夹钳单元结构

制动夹钳单元的结构如图2所示。制动夹钳单元的工作原理是利用杠杆原理把制动缸的推力转化为前端闸片托的夹紧力。

图2 某型制动夹钳单元结构示意图

3.2 制动夹钳单元有限元模型

制动夹钳单元的有限元模型如图3所示。

图3 制动夹钳单元有限元模型

分别将制动夹钳单元的材料属性、加载载荷、边界条件输入到有限元软件当中。其加载载荷与边界条件需要与其确认试验相对应。

在有限元模型验证与确认之前，需要对制动夹钳单元系统进行分层。本文采用传统分层方案，即：“系统→子系统→部组件(基准)→单元”的分层方案。其具体分层方案如图4所示。根据其分层方案，制动夹钳单元有限元模型的验证与确认分析过程从杠杆构件开始。

图4 制动夹钳单元重要构件分层结构

3.3 制动夹钳有限元模型验证

验证左边杠杆模型。确定其验证点位置，其验证点的位置如图5所示。再把校核点不同网格尺寸下的应力值带入验证方案并判断其有限元模型是否符合标准。

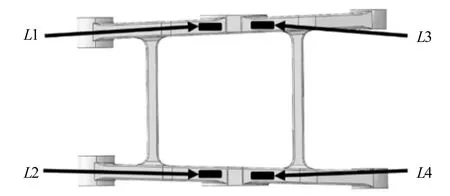
图5 左侧杠杆测点布置图

对于L1测点：载荷工况下，不同网格大小的L1测点的应力值如表1所示。

表1 在载荷工况下不同网格大小的L1测点应力值

结合上述验证方案可得

Δσ3=σ3-σ2=0.205 8

Δσ2=σ2-σ1=0.474 9

因此，在载荷工况下，测点L1周围网格为1.8 mm时符合验证方案的要求。

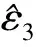
4 制动夹钳单元模型确认

4.1 制动夹钳单元确认试验

确认试验的原理是根据电阻应变测量技术使用电阻应变片测量测点应力值大小。需要注意的是确认试验的实际载荷工况与边界条件需要与有限元仿真计算时的载荷工况与边界条件一致，并且应变片的测点位置需要与有限元网格测点位置相一致。静强度试验现场如图6所示。

图6 制动夹钳单元静强度试验现场

为了确保试验数据的准确性，尽量排除随机误差的干扰，试验数据至少为100组，并整理出每个测点应变片的平均应力值与方差。整理好数据后与有限元模型的应力值进行确认对比。

4.2 制动夹钳有限元模型确认

制动夹钳有限元模型确认分析过程同样需要根据其分层方案，先确认每个构件之后再确认整个制动夹钳单元模型是否满足要求。

首先，确认左边杠杆模型，需要确认的测点如图5所示。先从L1测点开始，在载荷工况下的确认试验的平均应力测量值为21.4 MPa，方差为0.113。

结合上述的确认方案，可得：

MSRQ=0.06<0.1

因此，在载荷工况下，测点L1周围网格尺寸为1.8 mm时符合确认方案的要求。

同样的方法测得L2、L3、L4的MSRQ分别为0.110、0.048、0.076。测量结果表明：在网格大小为1.8 mm时，L1～L4共4个测点均符合确认方案要求。因此判定左侧杠杆计算模型满足仿真结果的准确性要求。利用同样的方法也可以判定其他构件仿真模型满足准确性要求。

5 总结

(1)对某型制动夹钳单元建模，并依据ASME V&V标准对计算模型进行验证与确认工作，最终确定其有限元分析模型的准确性满足标准要求。

(2)ASME V&V的灵活性的特点使得其普适性很强。因此能够广泛应用于轨道交通机械设备，可以评价整个轨道交通系统模型的准确性。

(3)对于制动夹钳单元模型，在能够确定模型准确性满足标准要求之前，对模型做出很多改动。其改动方向是：模型的加载载荷与边界条件尽可能靠近确认试验的加载载荷与边界条件。通过不断尝试，得到满足要求的制动夹钳仿真模型。

(4)本文所使用的有限元验证方案适用于多轴拉伸、扭矩和弯矩的载荷条件下的有限元模型。至于更复杂的有限元模型，该验证方案的适用性仍需要进一步研究。

(5)本文所使用的有限元确认方案不仅考虑到了试验数据的准确性，同时也考虑到了试验数据的波动性，因此较为客观、准确。

通过该型号制动夹钳单元有限元模型满足验证与确认流程条件分析过程，可以得出结论：该型号制动夹钳单元静强度有限元模型具有一定的准确性，可以直接通过有限元模型来确定其应力分布。进而可以把满足标准的建模方案推广到相类似的制动夹钳单元中，进而能够大大缩短其他类似制动夹钳单元研发与建模的时间。