基于MFAC的数控机床位置伺服系统

乔凌钰 费玉环,2 郑凯 马振伟,3 刘玥

0 引言

数控机床作为一种高精度机械零件加工的机电一体化设备,在生产制造业占据重要地位[1]．数控机床位置伺服系统是数控机床中很重要的组成部分,是一个多耦合和参数变化较大的非线性系统[2-3]，且系统的机械传动部分和永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有时变性和强耦合性的特点．当伺服系统模型的参数发生改变时,系统不能及时对其进行补偿．近年来,针对数控机床位置伺服系统的研究,国内外学者利用了多种算法,如模糊控制[3]、滑模控制[4]、迭代学习控制[5]、PID控制[6]等．滑模变结构适用于非线性系统,具有响应快、超调小、抗干扰能力强等特点,但易产生抖振．迭代学习控制能应用在非线性、模型不太确定的控制系统,且不需要知道被控对象的具体数学模型，已在扫描光刻系统[7]、永磁直线同步电机[8]中被应用,但是迭代次数较少、控制精度不高．线性模型一般用传统的PID控制器进行控制[9],但在实际应用中,由于位置伺服系统太过复杂,模型建立困难,PID控制很难实现．

本文采用的无模型自适应控制(Model-Free Adaptive Control,MFAC)[10]算法能够实现非线性系统的无模型自适应控制．该方法在类似位置伺服系统的一些时变、强耦合、强干扰的复杂系统中有一定的控制效果,且方法简单,不需要模型的信息,也无需人工对控制器进行参数调整,鲁棒性强且便于实现．MFAC算法提出时间相对较短,但已经在永磁同步电机驱动系统[11]、四旋翼飞行器[12]等控制对象中成功应用．MFAC方法目前在数控机床控制系统中还未广泛应用,因此无模型自适应控制算法有一定的应用潜力．

1 数控机床位置伺服系统的数学模型

本文采用dq坐标系下的PMSM的数学模型如下:

(1)

(2)

(3)

一般情况下,在常用的表贴式的永磁同步电机中Ld=Lq,所以:

(4)

以上各式中：ωr为相对于实际定子的角速度;Rs为定子绕组的电阻;Ld,Lq分别为定子d,q轴电感;ud,uq分别为定子d,q轴电压;id,iq分别为转子d,q轴电流;ψd,ψq分别为定子d,q轴磁链;Kt为电磁转矩系数．

如图1所示,基于PMSM的交流位置伺服系统一般采用三环控制结构,由内向外依次是电流环、速度环及位置环．电流环与速度环采用PI控制器,位置环采用P控制器．

2 基于改进前MFAC的位置伺服系统设计及仿真结果分析

2.1 基于改进前MFAC的控制器设计

本文在传统PI控制方式的基础上,采用紧格式动态线性化 (Compact Format Dynamic Linearization,CFDL)方法的无模型自适应控制方案对位置环与速度环进行设计，所设计出的基于MFAC的位置伺服系统如图2所示．其中电流环参数设置为Kpd=αLd,Kid=αRs,Kpq=αLq,Kiq=αRs,其滤波器系数α=2π/Ts,时间常数Ts=min{Ld/Rs,Lq/Rs}．

以q轴电流信号i、位置信号x作为系统的输入与输出,组成以下单输入单输出(Single-Input and Single-Output,SISO)离散时间的非线性系统方程:

x(k+1)=f(x(k),…,x(k-nx),i(k),…,i(k-ni)),

(5)

其中,i(k)与x(k)分别为位置伺服系统在k时刻的电流信号和位置信号,f(·)是未知函数,nx与ni是未知的正整数．

在给出动态线性化数据模型之前,作出如下符合位置伺服系统的假设:

假设1f(·)关于第(nx+2)个变量偏导数连续．

假设2系统满足广义Lipschikz条件,即对任意k1≠k2，i(k1)≠i(k2)有:

|x(k1+1)-x(k2+1)|≤d|i(k1)-i(k2)|,

(6)

其中：x(kx+1)=f(x(ke),…,x(ke-ox),i(ke),…,

图1 基于PMSM的交流位置伺服系统控制结构Fig.1 Control structure of an AC position servo system based on PMSM

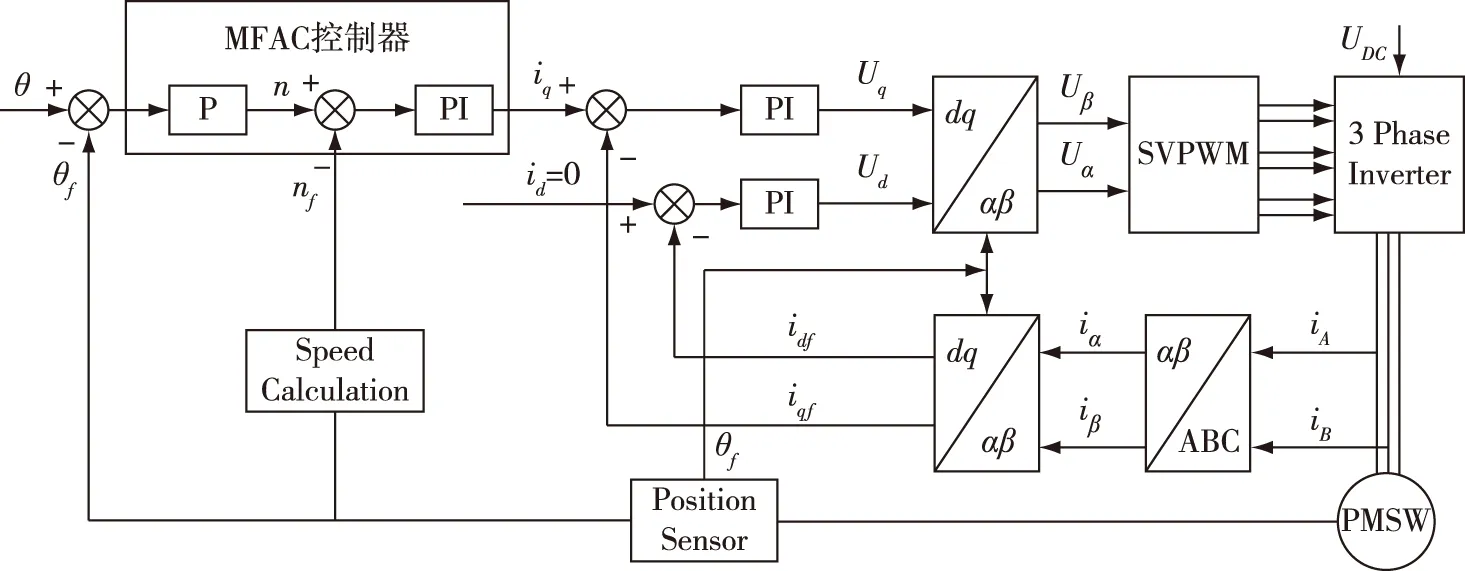
图2 基于MFAC控制方案的位置伺服系统Fig.2 The proposed position servo system based on MFAC

i(ke-oi)),e=1,2;d>0是常数．

假设3对某一给定的一致有界的系统期望输出信号x*(k+1),总存在一个有界的i*(k),使得系统在此控制输入信号的驱动下,输出等于x*(k+1)．

假设4对任意时刻k以及Δi(k)≠0,有φ(k)≥0,且在有限时刻内φ(k)=0．

当系统方程(1)满足假设1与假设2且|Δi(k)|≠0时,系统方程(1)等价于

Δx(k+1)=φ(k)Δi(k),

(7)

其中,φ(k)是伪偏导数(Pseudo-Partial-Derivative,PPD),是时变参数．

设控制输入准则函数为

J(i(k))=|x*(k+1)-x(k+1)|2+

λ|i(k)-i(k-1)|2，

(8)

图3 基于MFAC的位置伺服系统仿真框图Fig.3 Simulation block diagram of position servo system based on MFAC

其中,λ>0是权重因子,防止Δi(k)过大,x*(k+1)是期望跟踪信号．

为了使跟踪误差最小,令∂J/∂i(k)=0,得出控制算法为

(9)

其中,ρ∈(0,1]是步长．

由于φ(k)未知,需要对其进行估计,设PPD估计准则函数为

J(φ(κ))=|x(k)-x(k-1)-φ(k)Δi(k-1)|2+

(10)

其中,μ>0是权重因子．

令∂J/∂φ(k)=0得PPD估计算法为

(11)

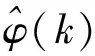
根据式(11)与式(9),得MFAC控制方案:

(12)

(13)

(14)

经证明,在满足上述所有假设情况下,满足:

1)|x*(k+1)-x(k+1)|≤N|Δi(k)|,N是常数;

2)当x*(k+1)=c,c为常数,存在正数λmin>0,当λ>λmin时,系统是有界输入-有界输出(Bounded Input Bounded Output,BIBO)稳定的．

因而系统是BIBO稳定的．

2.2 仿真结果分析

图3为基于无模型自适应的位置伺服系统仿真图,仿真条件为:直流测电压Udc=300 V,PWM开关频率fPWM=10 kHz,采样周期Ts=10 μs,采用变步长ode23tb算法,相对误差为0.001,仿真时间为0.3 s,给定电机转子旋转路程为1 mm,起始转矩为5 N·m,0.15 s时将负载转矩提升至10 N·m．图3仿真框图的参数如下:kp=15.6,ki=116 2,无模型自适应控制器参数为η=1.5,ρ=0.01,μ=1.5,λ=4．其电机参数如表1所示．

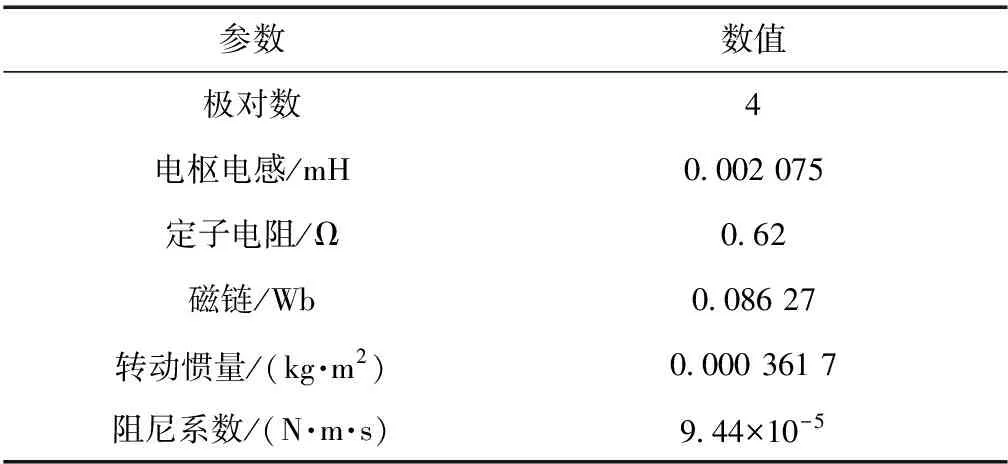
表1 PMSM参数

无模型自适应控制器仿真所得曲线如下:图4为位置跟随曲线,图5为转速响应曲线,图6为电磁转矩响应曲线,图7为三相电流曲线．

图4 位置跟随曲线Fig.4 Position following curve of MFAC

图5 转速响应曲线Fig.5 Speed response curve of MFAC

图6 电磁转矩响应曲线Fig.6 Electromagnetic torque response curve of MFAC

图7 三相电流曲线Fig.7 Three-phase current curve of MFAC

由图4可以看出,转子位置经过0.15 s,到达给定值1 mm,位置跟踪误差在10 μm左右．从图5可以看出,超调量较小，在前0.05 s内速度变化率高,转速最高达到了55 r/min,在0.02 s后,转速缓慢下降.从图6可以看出,启动时的电磁转矩波动大约为42 N·m,0.01 s时,变化剧烈,效果较差,0.06 s时,收敛到给定转矩5 N·m.从图7可以看出,在0.01 s以后,单相电流波动范围为6 A,三相电流开始稳定的时间为0.055 s,并且在0.15 s增大负载后,系统位置跟随几乎不受影响,转速有轻微波动,波动范围在0.5 r/min左右,电磁转矩产生超调量较小,且转矩变动未使电流产生明显超调,系统动态性能较好．

采用MFAC控制时,电机转速变化缓慢,位置响应曲线较为平稳,无超调量,系统稳定．但是此算法过于简单,PPD不能够在复杂的系统中充分地调节位置变化量与电流变化量的关系．且由图6可看出,电磁转矩在启动时的波动较大．

3 基于改进后MFAC的位置伺服系统设计及仿真结果分析

3.1 基于改进后MFAC的控制器设计

为进一步提高位置跟踪精度,改善系统动静态性能,并且保证控制算法的特性不变,这里通过增加比例和积分控制项来对紧格式MFAC的控制算法进行改进．所增控制项同样为时变参数,且改进后的算法适用范围更广泛．

对式(9)进行改进,设计以下控制算法:

e(k-1))+lie(k)),

(15)

其中,lp≥0与li>0是加权因子,而且e(k)为

e(k)=x*(k+1)-x(k).

(16)

从式(15)可以发现,此时的MFAC控制算法含有比例与积分的时变参数,控制算法(9)是控制算法(15)的特例,即当lp=0和li=1时,改进后的算法与改进前相同．

2) 当x*(k+1)=c,c为常数,系统的位置离散信号{x(k)}与电流离散信号{i(k)}有界,即系统是BIBO稳定的．

因此,闭环系统是BIBO稳定的．

3.2 仿真结果分析

改进后MFAC控制器的新增参数为lp=1,li=1.5．图8为位置跟随曲线,图9为转速响应曲线,图10为电磁转矩响应曲线,图11为三相电流曲线．

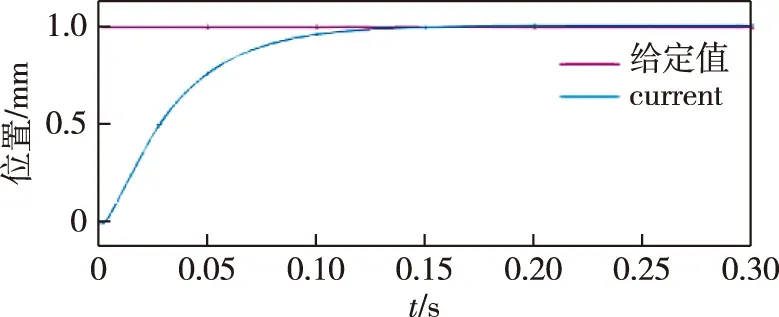
图8 位置跟随曲线Fig.8 Position following curve of improved MFAC

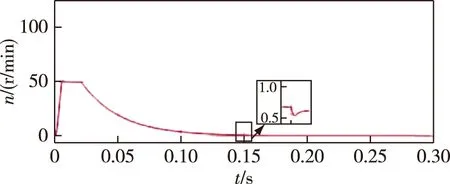
图9 转速响应曲线Fig.9 Speed response curve of improved MFAC

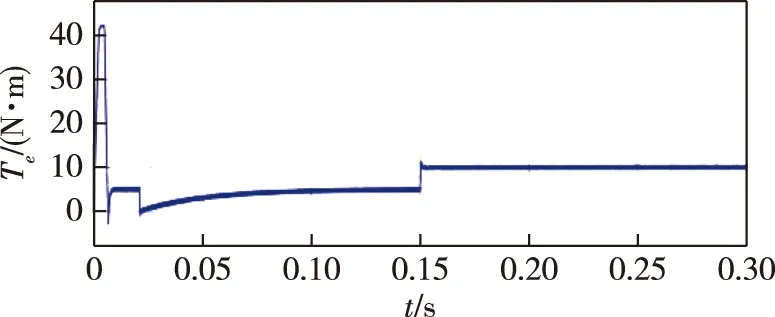
图10 电磁转矩响应曲线Fig.10 Electromagnetic torque response curve of improved MFAC

图11 三相电流曲线Fig.11 Three-phase current curve of improved MFAC

由图8可以看出,转子位置经过0.15 s,到达给定值1 mm,位置跟踪误差降到约1 μm．从图9可以看出,转速响应曲线无明显超调量,转速变化在前0.05内速度变化率高,最高达到了51 r/min,在0.01 s 后,稳定在50 r/min,在0.03 s后,转速下降．从图10可以看出,启动时的电磁转矩波动大约为41 N·m,在0.01 s时,变化过于剧烈，在0.06 s时,收敛到给定转矩5 N·m．从图11可以看出：启动0.01 s后,电流波动幅度较小,单相电流波动范围在5 A以内,因此控制器的动态性能优于改进前的MFAC;三相电流开始稳定的时间为0.055 s；此外,0.15 s时,由于变载导致的转速波动范围减小到0.25 r/min左右,说明系统的抗干扰能力有所提升,此时电磁转矩与电流均未出现明显的超调量,系统动态性能仍然较好．

与改进前MFAC控制的位置伺服系统相比,采用改进后的MFAC控制时,电机转速的稳定的时间更长,启动时转矩的波动幅度更小,位置跟随精度有所提高,系统的动静态性能均有一定提升．由此说明,改进后所设计的控制器的参数具有良好的动态性能和抗扰动能力,能够满足实际系统控制性能的需要．

4 结语

数控机床的位置伺服系统是一种典型的非线性、具有不确定性的时变系统．本文设计了两种基于MFAC控制的位置伺服系统,针对改进前MFAC控制算法过于简单的问题,增加时变比例与积分控制项来进行改进,设计了改进后的MFAC控制器．仿真实验结果表明,两种MFAC控制器都能实现对位置伺服系统的控制,并且改进后MFAC算法的位置跟踪效果更好,鲁棒性更强,更适用于高精度位置伺服系统中．