基于量化脉冲控制策略的领导跟随多智能体系统的固定时间一致性

董鑫淼 李传东 王欣 曹正然

0 引言

随着人工智能的发展,多智能体系统[1]作为人工智能的一个重要分支,受到了广泛的关注并成为研究的热点.在各学科专家、学者的共同努力下,多智能体系统在一致性[2-3]、同步[4-5]、群集[6-7]、协调[8-9]、优化控制[10]等领域取得了丰硕的成果.此外,关于一致性问题有两个常见的研究方向,一个是领导跟随模型[11],另一个是无领导监督模型[12].

领导跟随一致性[13-16],意味着多智能体系统内,跟随者的动态行为要与领导者达到统一.需要指出的是,一致性类型有很多,如渐近一致性[17]、指数一致性[18]、有限时间一致性[19]、固定时间一致性[20-21]等.指数一致性作为一种特殊的渐近一致性,已经被很多学者研究.然而,渐近一致性和指数一致性通常是在时间趋于无穷时实现的,这在现实生活中很难实现.近年来,有限时间一致性的概念被提出,解决了渐近一致性和指数一致性的缺陷,且达到一致的时间是可计算的.但它仍有缺陷,因为该时间依赖于系统的初始状态.作为一种特殊的有限时间一致,固定时间一致是避免这种缺陷的好方法[22-24].但现有关于领导跟随多智能体系统的文献中,研究固定时间的成果相对较少.因此,研究领导跟随多智能体系统的固定时间一致性具有重要的意义.不失一般性,本文建立的是最基本的非线性领导跟随多智能体系统模型.

当多智能体之间的连接很弱时,没有控制器就很难实现系统的同步.迄今为止,已经发表了很多控制方案,如自适应控制[25]、事件触发控制[26-27]、协同控制[28]、脉冲控制[29]、状态反馈控制[30]、采样数据控制[31]、间歇控制[32]等.脉冲控制是一种典型的控制方法,广泛应用于生物、医学、物理、航天等领域.一方面,系统不可避免地会受到干扰和中断,脉冲效应可以很好地模拟状态的突变；另一方面,它可以有效缓解信息传递的压力.

由于通信信道的比特率、能量和带宽是有限的,信息量化[33]在控制方案中起着重要作用.一般有两种量化器:均匀量化器[34-36]和对数量化器[37-39].本文考虑对数量化器.

考虑到上述几个因素,本文通过量化脉冲控制的方法分析了非线性领导跟随多智能体系统的一致性问题.本文的新颖之处在于:1)建立领导跟随多智能体系统模型,并设计了合适的控制协议;2)将通信数据量化,且在脉冲时刻进行系统内的信息交换,大大降低了通信带宽和能耗;3)所建立的模型是最基本的非线性多智能体系统.

本文的其余内容如下所示:第1节是预备知识,并介绍一些必要的假设、定义和引理;第2节建立了非线性领导跟随多智能体系统模型,并基于李雅普诺夫函数给出了定理;第3节通过选择合适的参数进行仿真,验证了上述理论分析的正确性;第4节是结论.

注1本文中,R表示实数集,IN表示N×N单位矩阵,XT表示矩阵X的转置矩阵,diag(x1,x2,…,xN)表示N×N对角阵,max{xi}表示x1,x2,…,xN的最大值.令M为一个实对称矩阵,则M>0(M<0)表示正(负)定矩阵.

1 预备知识

1.1 图论

通过计算L=D-A可以得到拉普拉斯矩阵L=(lij)N×N,其元素满足:

(1)

1.2 对数量化器

量化器关于原点对称,且满足Q(m)=(1+Ξi)m,∃Ξi∈[-ζ,ζ].而且,如果m∈Rn,有Q(m)=(Q(m)1,Q(m)2,…,Q(m)N).

1.3 假设和相关引理

在这部分,将介绍后续证明需要用到的假设、定义和引理．

假设1给定利普希茨常数lf>0满足

|f(t,sj(t))-f(t,si(t))|≤lf|sj(t)-si(t)|.

假设2给定利普希茨常数lξ1,lξ2,…,lξN>0满足|ξi(sj(t))-ξi(si(t))|≤lξi|sj(t)-si(t)|,其中i=1,2,…,N.

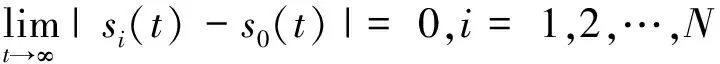
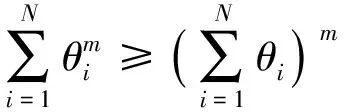
引理3[42]假设在(t,T)区间上有脉冲序列τ=t1,t2,…,令T表示平均脉冲间隔,Kξ(t,t0)表示给定区间内的脉冲次数,存在K0∈N+和T∈R+满足

2 主要结果

本节建立了领导跟随多智能体系统模型．此外,通过构造李雅普诺夫函数得到了同步标准和一些充分条件,证明了领导跟随多智能体系统在量化脉冲控制下的固定时间一致性,并给出了同步时间.

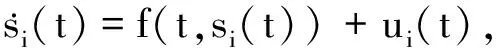
(1)

其中,xi∈R描述第i个多智能体的状态,f:R×R→R是一个非线性函数,且ui∈R是第i个多智能体的控制协议.

标记为0的多智能体称为领导者,是根据实际情况设定的理想目标轨迹,s0(t)可以被动态描述为

(2)

第i个多智能体的控制协议被设计为

(3)

其中,控制参数α,β>0,x，y，p和q都是正奇数,且满足xp.

在控制协议(3)下,系统(1)被改写为

(4)

令ci(t)=si(t)-s0(t),可以得到误差系统.

(5)

定理1假定假设1和2满足且γk∈(0,1).当(IN+GΞ+G)T(IN+GΞ+G)-γkIN<0时,非线性多智能体系统(4)将在固定时间内达到领导跟随一致性,一致时间为

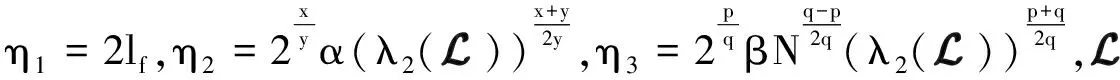
(6)

根据假设1,有

(7)

其中,η1=2lf>0.

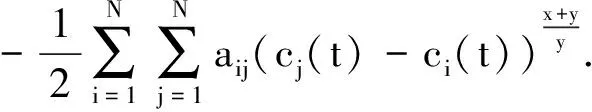
(8)

根据引理4,有

(9)

(10)

综上所述,李雅普诺夫函数可以被改写为

(11)

当t=tk时,

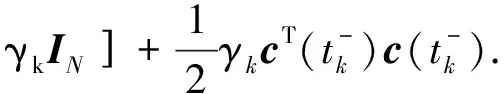
(12)

由于(IN+GΞ+G)T(IN+GΞ+G)-γkIN是负定的,因此

(13)

方便起见,用γ=max{γ1,γ2,…,γk}来代替γk.

根据式(6)—(13),可以推导出

(14)

因此构建如下比较系统[45]:

考虑0<γ<1,为了方便计算,当ν(t)≥1时,假设r(t)=ν1-ω(t),式(15)可改写为

其中,γ1=γ1-ω≥1.如果画出r(t)关于ν(t)的曲线,可以看出连续部分大致是下降的,且当ν(t)→1时,r(t)→1,当ν(t)→∞时,r(t)→0.

式(16)的解可以通过数学归纳法[46]求出.

(18)

接下来求解T1,

(19)

(20)

(21)

(22)

接下来考虑另一种情况0<ν(t)<1,设定r(t)=ν1-υ,可以得到

(23)

其中0<γ2<1满足γ2=γ1-υ.如果画出r(t)关于ν(t)的曲线,可以看出连续部分大致是上升的,且当ν(t)→1时,r(t)→1,当ν(t)→0时,r(t)→0.

通过数学归纳法,可推出

(24)

这表明r(t)是单调递增的,且r(T1)=1.

因此,式(24)可以重写为

(25)

t-T1=2TaN0+

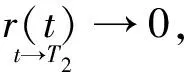
T2=2TaN0+

(26)

根据上述分析可以得到同步时间为

T=T1+T2=

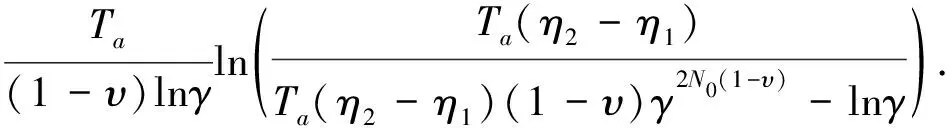
(27)

注2估算的T值是最大同步时间,且不确定是在连续时间还是脉冲跳变点.

3 数值仿真

本节选择一些合适的参数通过仿真验证以上理论分析的有效性．

考虑如下多智能体系统,网络拓扑如图1所示．

图1 网络拓扑图Fig.1 Network topology map

和

其中,s0是一个孤立的控制节点,满足初始值s0(0)=0.5,其余4个多智能体满足初始值为s0(0)=[-0.1,-2.7,1.8,2.4]T.F(t,m(t))=[f(t,m1(t)),f(t,m2(t)),f(t,m3(t)),f(t,m4(t))].f(t,mi(t))=cos2(mi(t))-|sin(mi(t))|,满足常数为lf=[1,1,1.8,1.2]T的利普希茨条件.如图2所示.s(t)的拉普拉斯矩阵为

令步长为0.000 1,脉冲间隔为0.002,脉冲增益γ=0.8.取α=4.3,β=2.5,x=1,y=3,p=5,q=3.经过计算得,η1=4.4,η2=9.798 8,η3=16.459 1,且

(IN+GΞ+G)T(IN+GΞ+G)-γkIN<0也满足.

0.173 8s.

显而易见,定理1是有效的,图2展示了跟随者将在约0.18 s的位置与领导者达到一致.

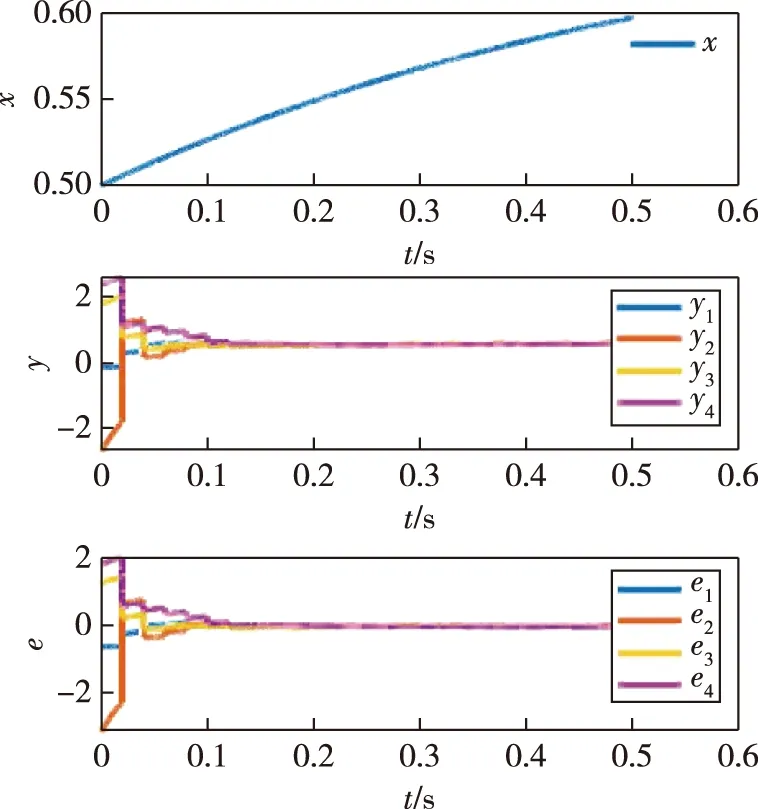
图2 在脉冲控制下s(t)中的每一个节点都与s0(t)达到一致Fig.2 Every node of s(t) achieves soon consensus with s0(t) under impulsive control

4 结论

通过选择合适的脉冲控制协议,解决了非线性领导跟随多智能体系统的固定时间一致性问题.为减少通信损失,脉冲控制协议保证多智能体系统内的多智能体在脉冲时刻进行信息交互.利用李雅普诺夫函数、凸分析和利普希茨条件,得到了两个充分条件,使系统在固定时间内达到一致,该时间可计算且与初始状态无关.最后通过仿真验证了理论推导的可行性.