复合材料螺旋桨水动力性能与结构响应数值研究

刘影, 张晶, 吴钦, 张汉哲, 黄彪

(北京理工大学 机械与车辆学院，北京 100081)

传统金属螺旋桨存在阻尼性能差，易产生振动及噪声、易空蚀、易疲劳破坏等问题，这直接影响到螺旋桨服役寿命和军用舰船的生存能力[1].复合材料具有高阻尼、轻质高强、耐腐蚀、可设计性强等优点，且可通过改变纤维铺层角度及方式来控制结构变形，因此应用复合材料制造螺旋桨为改善其水动力性能及结构特性提供了新的契机[2-3].

为探究复合材料对螺旋桨性能的改善效果，Young[4]将边界元法与有限元法相结合，进行复合材料螺旋桨水动力数值计算，对螺旋桨尺寸效应、弯扭耦合效应及推进效率进行分析，结果表明有限元法可以很好地计算结构响应且精度较高，边界元法计算速度快但精度稍逊，复合材料特有的各向异性可以提高螺旋桨自适应性并改善螺旋桨推进性能.He等[5]基于较高精度的CFD耦合FEM方法对复合材料螺旋桨展开计算，结果表明复合材料螺旋桨的水弹性及结构响应均大于金属螺旋桨，且变形后的螺旋桨外形对流场有较大影响.洪毅[6]应用商业软件ANSYS，根据有限元原理对复合材料螺旋桨进行铺层建模，分析了该螺旋桨的敞水性能、刚度及强度，采用预变形策略并结合稳态流固耦合计算结果，实现了复合材料螺旋桨的外形重构和性能优化.由于复合材料良好的可设计性为结构性能优化提供了契机，大量学者针对不同铺层方式的复合材料螺旋桨进行了研究.Lin等[7]对两种不同铺层的复合材料螺旋桨的水动力性能展开了数值和实验研究，结果表明复合材料应用于螺旋桨可以提高其推进效率.陈悦等[8]为探究复合材料铺层对螺旋桨性能的影响，对±45°对称铺层的螺旋桨进行双向流固耦合稳态求解，得到各进速系数工况下的敞水性能.

虽然复合材料螺旋桨双向流固耦合相关研究已得到不少学者的关注，但主要集中在复合材料螺旋桨水动力性能的预报，因复合材料的应用而使螺旋桨推进性能得到改善的机理仍未得到很好的理解，仍需对复合材料螺旋桨的结构响应进行深入研究.文中以大侧斜螺旋桨为研究对象，建立复合材料螺旋桨双向流固耦合数值计算方法，在课题组相关研究的基础上[9-12],研究了不同进速系数和不同铺层角度工况下该螺旋桨的水动力性能和结构响应特性，以期为我国高性能复合材料螺旋桨的设计提供帮助.

1 数值模型及方法

1.1 复合材料螺旋桨结构模型

文中以Seiun-Maru船用大侧斜螺旋桨(HSP)为研究对象，该螺旋桨几何参数如表1所示.根据坐标变换原理推导出螺旋桨叶切面局部坐标系到全局坐标系的变换公式，利用Matlab进行编程将螺旋桨叶切面型值转换得到桨叶三维坐标点，进而得到螺旋桨几何模型如图1所示.

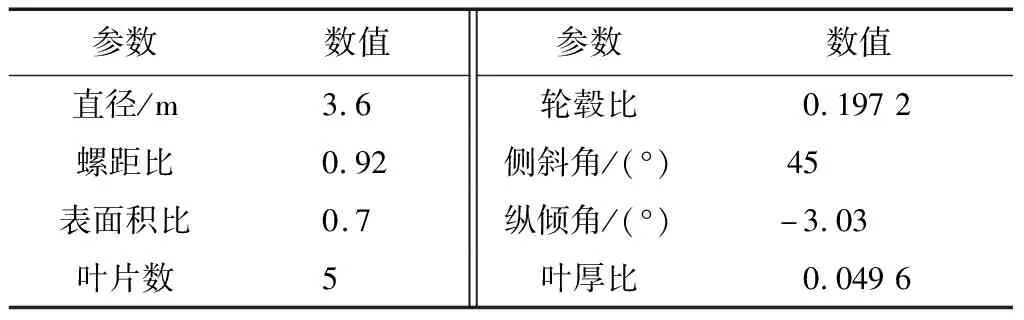
表1 螺旋桨几何参数

图1 大侧斜船用螺旋桨(HSP)

文中以玻璃纤维增强环氧树脂复合材料为螺旋桨的建模材料，材料参数如表2所示.相较于该螺旋桨原用金属材料(AlBC3,ρ=7 500 kg/m3)，本文所述复合材料螺旋桨有明显的减重效果.如图2所示，该复合材料螺旋桨铺层方式为[θ]25，其中θ为玻璃纤维与局部坐标系X轴的夹角，下标25表示总铺层数，从螺旋桨导边指向随边定义为纤维0°铺层方向.

表2 材料参数

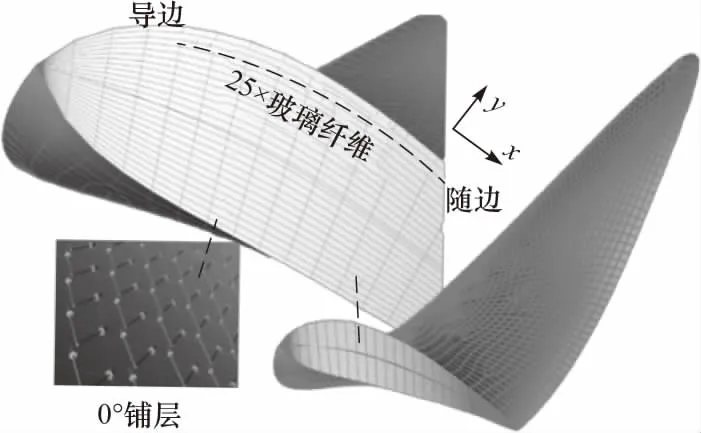
图2 复合材料螺旋桨铺层

1.2 复合材料螺旋桨数值计算方法

1.2.1流场控制方程

螺旋桨运动速度通常较小(Ma<0.3)，因此可以认为螺旋桨周围流场为典型的三维不可压湍流流动，其连续性方程和动量方程为

(1)

(2)

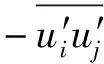
(3)

式中:k为湍动能;w为湍流频率;σw和σk分别为湍动能和湍流频率的普朗特数;Pk和Pω为湍动能生成项;Yk和Yω为湍动能耗散项.

1.2.2结构场控制方程及流固耦合计算方法

复合材料螺旋桨旋转时叶片受到水动力载荷和离心力作用而产生变形，变形后的桨叶将改变螺旋桨周围流场，同时流场的变化又将再次影响桨叶结构的变形.桨叶结构在水动力作用下的控制方程为

(4)

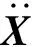
如图3所示，流场计算域分为静止域与旋转域，考虑到尾流及湍流耗散的影响，在流域入口端设置长0.7D的静止域来充分模拟船尾流场以保证计算收敛性[13].流域入口均匀来流，出口定义为压力出口，桨叶和桨毂为无滑移壁面，静止域和旋转域间采用动静交界面连接.为精确捕捉叶片表面压力脉动和桨叶负载，在旋转域内部螺旋桨周围建立半径为0.6D的小圆柱体域，采用适应性较强的非结构网格并作加密处理.如图4所示，为保证计算精度，在螺旋桨导边、随边及叶根处生成边界层网格使叶片表面y+与湍流模型相匹配.静止域与旋转域均采用六面体单元进行结构化网格划分，整个流场计算域总网格数为632万.

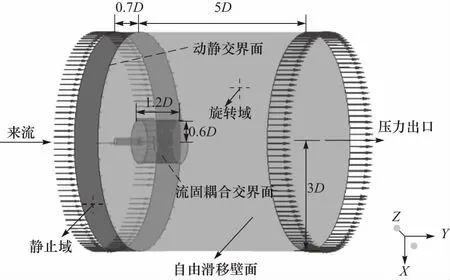
图3 流域划分及边界条件

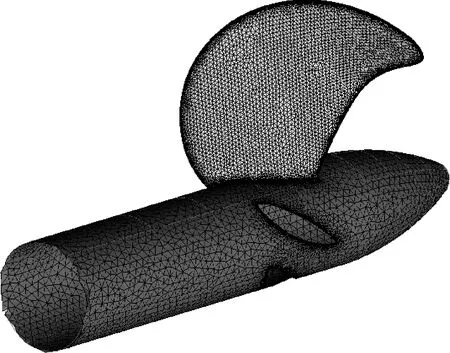
图4 桨叶表面网格

由于螺旋桨水动力载荷压力梯度较大且高度非线性，故采用三维20节点SOLID186 单元对复合材料桨叶进行结构化网格剖分，整个结构场总网格数为12万.复合材料螺旋桨有限元模型如图5所示，螺旋桨旋转速度与流场保持一致为90.7 r/min，桨叶根部为固定端约束，叶片表面为流固耦合交界面可实现结构场与流场间力和位移的数据传递.采用分步耦合算法[12]计算复合材料螺旋桨的流固耦合特性，图6为所用算法的流程图.计算过程中，先计算流场水动力载荷，载荷数据通过流固耦合交界面(Interface)传递到结构场，桨叶结构在载荷作用下发生变形，流场根据结构场的变形进行网格更新再次进行计算得到新的载荷.结构场与流场计算交替进行，直至传递的载荷数据及网格变形数据的残差达到设定的收敛标准，即两者均小于0.01.

图5 复合材料螺旋桨有限元模型

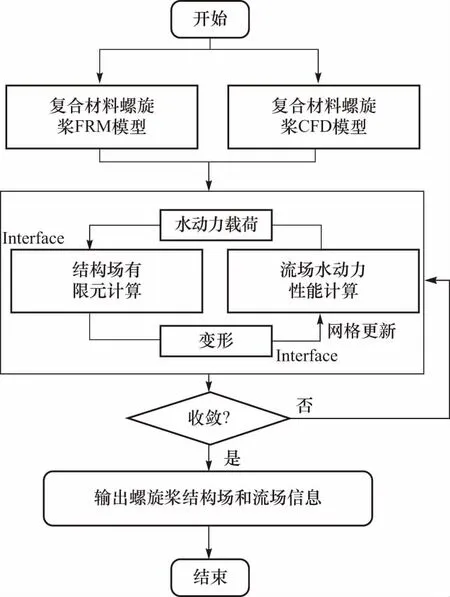
图6 流固耦合算法流程图

1.2.3数值方法验证

螺旋桨水动力性能主要包括螺旋桨在水中旋转产生的推力、扭矩及其推进效率，相应的量纲一的参数为：扭矩系数(KT=TQ/ρn2D5)、推力系数(KF=FT/ρn2D4)及推进效率(η=JKF/2πKT).式中TQ为5个桨叶的扭矩之和，即总扭矩；n为螺旋桨转速;D为螺旋桨直径；FT为5个桨叶上的推力之和，即总推力；J表示进速系数J=U/(nD)，其中U为来流速度.为了准确地求解HSP螺旋桨的水动力性能，在无空化非均匀来流条件下，选取实验工况(J=0.851,n=90.7 r/min)进行数值计算，并将计算结果与实验结果[14]进行对比，如表3所示.结果表明，计算误差低于8%，与实验结果具有较高吻合度，验证了数值计算方法的正确性.

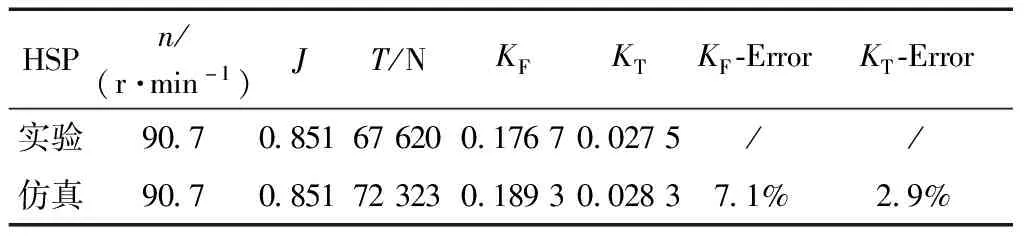
表3 数值与实验结果对比

2 结果和讨论

2.1 进速系数对复合材料螺旋桨水动力性能与结构响应的影响

不同进速系数工况下桨叶将受到不同的水动力载荷，进而产生不同的变形而影响复合材料螺旋桨的水动力性能.为了研究不同进速系数工况下复合材料螺旋桨水动力性能的变化，图7给出了在J=0.2～1.0工况下复合材料螺旋桨与刚性金属螺旋桨的水动力性能对比.当铺层角度一定时，随进速系数增加，复合材料螺旋桨的扭矩系数(复合材料-KT)和推力系数(复合材料-KF)基本呈减小趋势，推进效率(η)呈先增加后减小趋势，在进速系数J=0.8时取得最大值0.75.当进速系数超过0.8时，推进效率开始减小，且在设计工况J=0.851时复合材料螺旋桨推进效率低于金属螺旋桨.由图可知，在J<0.8所有非设计工况中复合材料螺旋桨的推进效率明显高于金属螺旋桨，证实了复合材料的应用可以提高螺旋桨的推进效率.

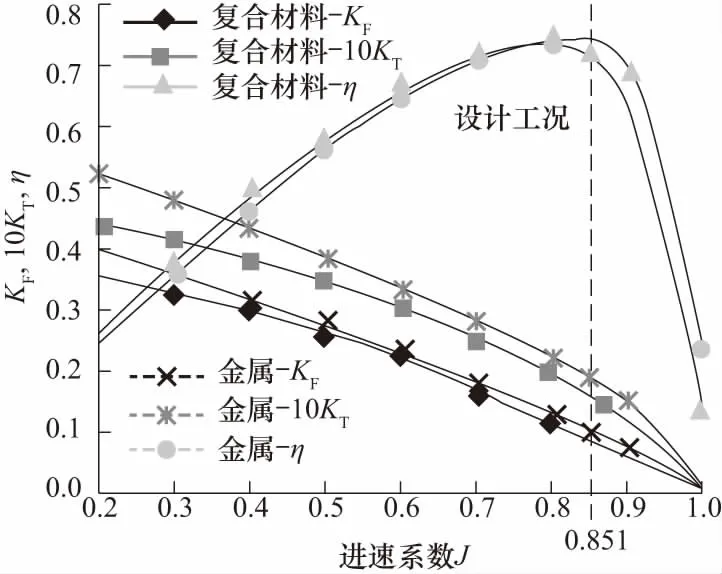
图7 复合材料螺旋桨与刚性螺旋桨的水动力性能对比

为了进一步分析不同进速系数下复合材料螺旋桨的结构响应和其推进效率较金属螺旋桨提高的原因，图8和图9分别展示了该复合材料螺旋桨在不同进速系数下桨叶在各半径处侧斜和纵倾相较于金属螺旋桨的变化情况，其中横坐标为螺旋桨叶切面半径，纵坐标为螺旋桨几何特征.从图8可知，在该铺层工况下，不同进速系数下复合材料螺旋桨各半径处的侧斜基本保持不变，其大小与金属螺旋桨无明显差异.从图9可知，复合材料螺旋桨的纵倾比金属螺旋桨在0.8R～0.95R处有明显减小，在0.8R前因复合材料桨叶变形较小使得其纵倾几乎没有变化.

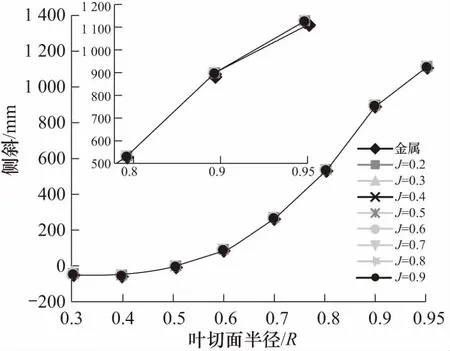
图8 不同进速系数下桨叶在各半径处侧斜的变化

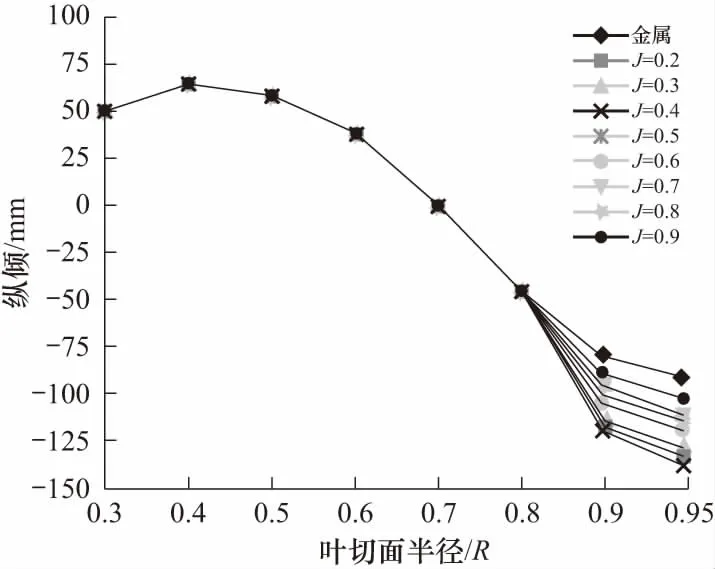
图9 不同进速系数下桨叶在各半径处纵倾的变化

不同进速系数下复合材料螺旋桨叶在各半径处的螺距角相较于金属螺旋桨的变化如图10所示，各进速系数工况中复合材料螺旋桨在各半径处的螺距角变化趋势一致，均是因桨叶产生变形使其螺距角减小且均小于同工况下的金属螺旋桨.如图11所示，根据桨叶速度三角形，当螺旋桨旋转速度u不变，而进速系数增加，也即来流速度变大时，相对速度w与绝对速度v间的夹角β减小，也即攻角减小，刚性的金属螺旋桨因螺距角保持不变而与攻角的减小不匹配导致推进效率降低，而图12所示的复合材料螺旋桨叶片因产生扭转变形使螺距角α减小，正好与攻角的变化相匹配，进而自适应地提高了复合材料螺旋桨的推进效率.

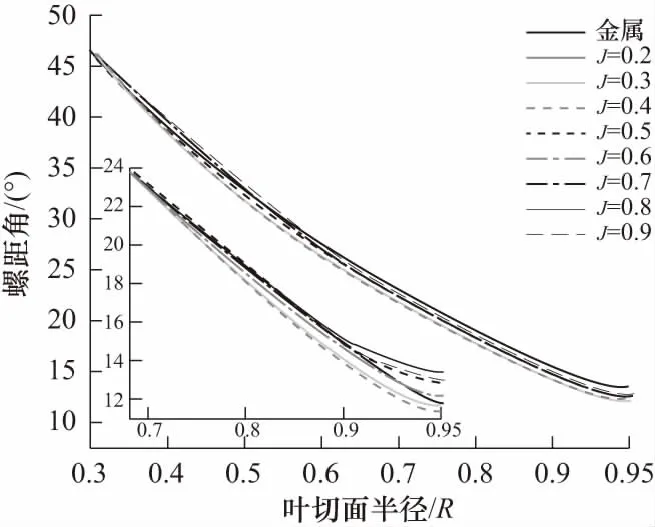
图10 不同进速系数桨叶在各半径处螺距角的变化

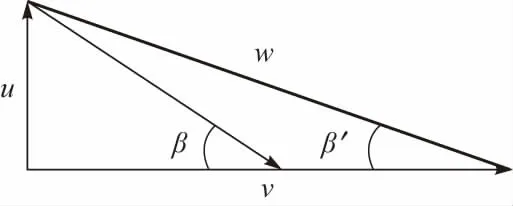
图11 复合材料螺旋桨桨叶速度三角形

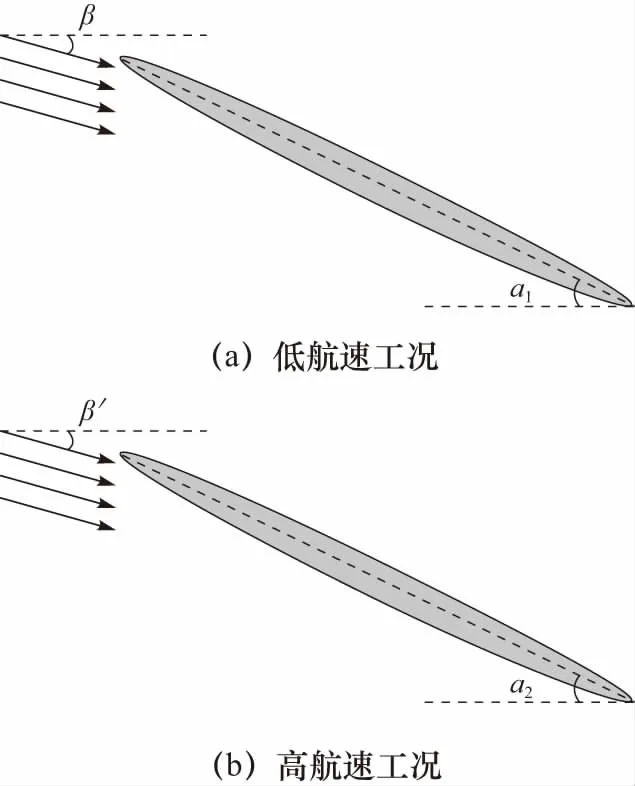
图12 不同航速工况复合材料螺旋桨的自适应特性

2.2 铺层角度对复合材料螺旋桨水动力性能与结构响应的影响

为研究铺层角度对复合材料螺旋桨水动力性能的影响，图13给出了在进速系数J=0.3工况下不同铺层角度复合材料螺旋桨的敞水性能，其中横坐标为铺层角度，纵坐标为水动力性能参数，黑色虚线代表刚性的金属螺旋桨，实线代表复合材料螺旋桨.由图可知，随复合材料铺层角度增加，复合材料螺旋桨的扭矩系数KT和推力系数KF先增大后减小，且增大和减小的趋势几乎一致.推力系数和扭矩系数在90°铺层时最小，30°铺层时最大.推进效率的变化趋势与KT和KF正好相反，呈先减小后增大的趋势，推进效率在90°铺层时最高，30°铺层时最低.与金属螺旋桨相比，上述铺层角度的复合材料螺旋桨的推进效率均高于金属螺旋桨.

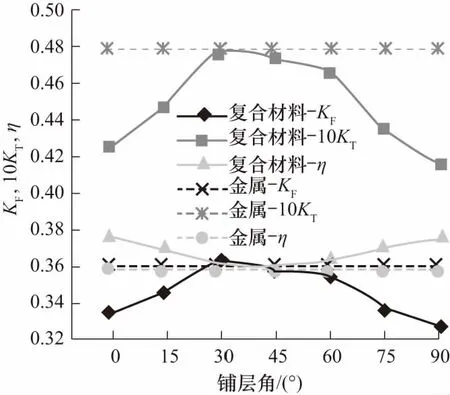
图13 不同铺层角度工况复合材料螺旋桨的水动力性能

图14给出了金属螺旋桨与0°，60°，90°铺层复合材料螺旋桨在压力面和吸力面上的压力分布对比.两种材料的螺旋桨压力分布差异显著，金属桨叶压力面与吸力面间压差明显大于复合材料桨叶，这与图7所示的金属螺旋桨的推力系数KF较高相对应.金属桨叶整个压力面上的压力较高；吸力面上导边压力最高，随边附近区域次之，叶片中部压力分布较低且均匀.复合材料桨叶压力面上导边附近压力较高，叶梢及叶根接近导边处压力较低，不同铺层角度工况压力面上压力分布的区别在于低压区面积的大小，三者中60°铺层桨叶低压区面积最大，90°铺层次之，0°铺层最小.复合材料桨叶吸力面上压力分布变化不大，压力值从随边朝导边逐渐递减，在导边偏叶梢处达到最低.

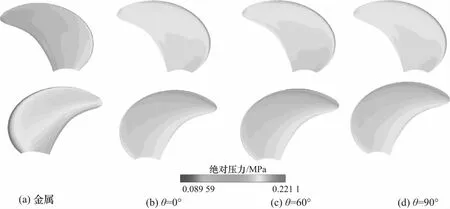
图14 金属螺旋桨与0°、60°、90°铺层复合材料螺旋桨压力面(上)和吸力面(下)上的压力分布的对比

为了分析不同铺层角度复合材料螺旋桨的结构响应特性，图15给出了桨叶最大总变形与最大等效应力随铺层角度的变化曲线.由图可知，铺层角度对复合材料桨叶结构响应的影响十分显著.桨叶最大总变形随铺层角度先减小后增加，60°铺层工况桨叶最大总变形量最小，0°铺层工况最大.最大等效应力随铺层角度先增加后减小再增加，其中0°铺层工况的最大等效应力值最小，90°铺层工况最大.

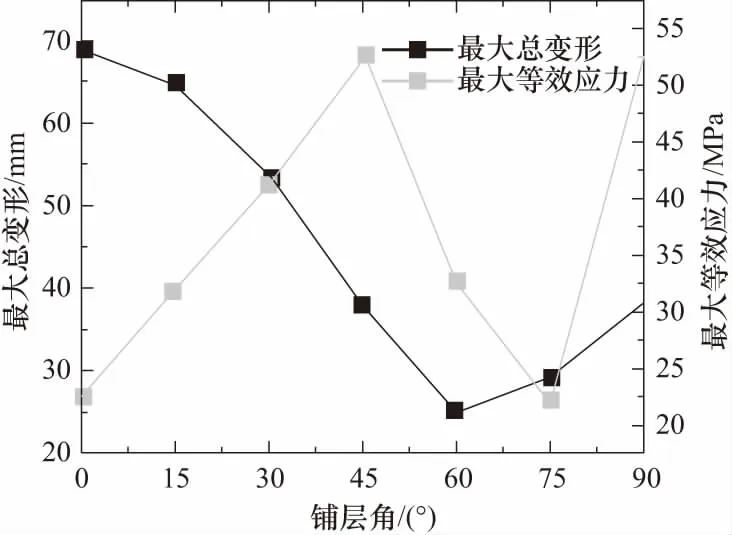
图15 最大总变形及最大等效应力随铺层角度的变化

图16展示了0°，60°，90°三个典型铺层工况下复合材料螺旋桨的总变形和等效应力分布.各铺层工况下桨叶总变形分布趋势一致，均是沿叶根到叶梢形变量逐渐递增，叶梢的形变量最大，桨叶中下部几乎没有变形.铺层角度对桨叶结构变形有显著影响，0°铺层工况桨叶变形最大，达到了69 mm，60°铺层工况桨叶变形最小.各铺层工况的桨叶等效应力分布趋势相似，从叶面外围到中心呈环状分布且应力逐渐增加.桨叶导边、随边及叶梢均处在低应力状态，叶根部分及叶面上部偏随边处有较高应力区域，叶梢处变形最大但等效应力值却很低.

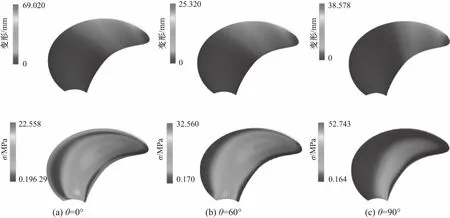
图16 0°，60°，90°铺层工况下复合材料螺旋桨桨叶总变形及等效应力分布

3 结 论

基于CFD计算复合材料螺旋桨水动力性能，应用有限元法计算桨叶结构响应，建立了复合材料螺旋桨在均匀来流下的双向流固耦合数值模拟，开展了不同进速系数及不同铺层角度下复合材料螺旋桨的水动力性能及结构响应的研究工作，研究结果如下.

① 随进速系数增加，复合材料螺旋桨的扭矩系数和推力系数减小，推进效率先增加后减小.在进速系数J≤0.8时，复合材料螺旋桨的推进效率相较于同工况下的金属螺旋桨有明显地提高.

② 航速增加时，复合材料螺旋桨的螺距角较金属螺旋桨减小，侧斜几乎保持不变，纵倾在0.8R～0.95R处减小.金属螺旋桨因螺距角固定不变而与攻角变化不匹配导致推进效率降低，而复合材料螺旋桨因弯扭耦合变形使得螺距角减小，自适应地提高了推进效率.

③ 随铺层角度增加，复合材料螺旋桨扭矩系数和推力系数先增大后减小，推进效率先减小后增大，所有铺层角度工况的复合材料螺旋桨的推进效率均高于金属螺旋桨, 铺层角度对复合材料桨叶结构响应影响显著.