高超声速目标拦截末段交战窗口快速生成方法

梁子璇，郭 栋，朱圣英，任 章

(1. 北京理工大学宇航学院，北京 100081；2. 深空自主导航与控制工信部重点实验室，北京 100081；3. 中国运载火箭技术研究院，北京 100076；4. 北京航空航天大学自动化科学与电气工程学院，北京 100191)

0 引 言

高超声速飞行器能够依靠气动升力在临近空间远距离飞行，可执行快速侦察或打击任务。此类飞行器弹道灵活，若采用特定的威胁规避制导技术，则将具备极强的机动突防能力[1-4]。因此，高超声速飞行器一旦用作武器，将给现有的导弹防御系统带来巨大威胁。为了应对这种威胁，必须发展专门针对高超声速目标的先进拦截技术[5-6]。

拦截器的弹道一般分为三个阶段[7]：初始段(或发射段)、中制导段(或巡航段)、末制导段(或交战段)。中制导段的使命是为末制导段交战提供有利的初始阵位。所有可行的初始阵位构成末段交战窗口(Terminal engagement window, TEW)，拦截器只有从窗口内出发，才有能力实现对目标的拦截。相关研究中，TEW也称为攻击区、捕获区或发射区[8-11]。窗口边界的计算问题可以归结为求解不同方向上的最远(最大)和最近(最小)距离[12]。当评估某一方向上的某一距离是否位于窗口之内时，常用的方法是：在特定导引律下，通过数值积分得到拦截弹道，再根据最终的脱靶量等指标来做出判断。黄国强等[12]通过大规模的飞行轨迹仿真，计算出了空空导弹的三维攻击区。在此基础上，吴胜亮等[13]研究了升阻比和随机风场对空空导弹三维攻击区的影响。进一步，Hui等[14]针对随机风场影响，建立了考虑时间变化的四维攻击区生成方法。由于最远、最近距离的优化过程涉及到飞行轨迹的数值积分，故此类方法的求解效率低，在线使用难度大，不满足高超声速目标拦截的快速响应需求。

临近空间高超声速目标具有速度高、过载小的特点，其转弯能力远低于空空导弹，这为建立解析形式的拦截条件提供了可能。Tyan[15]针对高速非机动目标，基于纯比例导引律研究了视线坐标系下的拦截条件，并在速度前置角(速度方向与弹目视线方向的夹角)平面建立了捕获区。在此基础上，Wang等[16]基于反比例导引律研究了视线坐标系下的拦截条件，并给出了拦截器的最优初始位置和速度方向。周觐等[17]针对高超声速目标，分析了比例导引律和反比例导引律对应的捕获区，并得到了相同条件下后者大于前者的结论。然而，这些研究中的捕获区都建立在速度前置角坐标系，不能给出直观的交战几何关系，此外，拦截条件也都是针对非机动目标建立的。

本文针对巡航段和平衡滑翔段的高超声速目标，研究水平面的TEW快速生成方法。首先，结合高超声速目标及拦截器转弯半径大的特点，建立解析形式的拦截条件。在此基础上，针对非机动目标和机动目标，依次推导TEW边界的解析方程。同时，为寻找TEW内相对有利的交战位置，引入了拦截器初始航向角可控裕度的概念。最后，通过仿真验证了所提出方法的有效性，分析了TEW边界和可控裕度的影响因素，并与传统数值方法进行了对比。

1 拦截运动建模

对于巡航段和平衡滑翔段的临近空间高超声速目标，其纵向弹道受到热流密度、动压、过载等多种约束，纵向机动能力较弱[7]。为此，本文忽略拦截器与目标在纵向平面的相对运动，针对水平面的阵位关系建立二维交战窗口。首先，对末制导段拦截运动做出如下假设：

假设1. 拦截器与目标位于相同的高度，仅考虑二者在水平面的相对运动；

假设2. 末制导段持续时间较短，拦截器与目标的速度大小均为常值。

末制导段初始时刻，拦截器与目标的相对运动关系如图1所示。图中，M和T分别代表拦截器和目标，坐标原点为目标初始位置，x轴与目标初始速度方向重合。变量vT和nT分别为目标的速度大小和法向过载。拦截器位置由相对距离r和视线方向θ决定，速度大小为vM，法向过载为nM，速度前置角为ηM，弹目视线角为qM，航向角为ψM。

图1 拦截器与目标的相对运动关系Fig.1 Engagement geometry of interceptor and target

由此，建立目标与拦截器的运动方程

(1)

(2)

式中：(xT,yT)和(xM,yM)分别为目标和拦截器的位置，ψT和ψM分别为目标和拦截器的航向角。由于目标初始速度方向与x轴重合，故有ψT(0) = 0。拦截器的初始航向角为

ψM(0)=π+θ0+ηM(0)

(3)

式中：ηM(0)为拦截器初始速度前置角。进入末制导段时，为使导引头捕获目标，应满足视场角约束。若最大视场角为ηField，则有

-ηField≤ηM(0)≤ηField

(4)

此外，目标和拦截器的机动能力也均受到约束，表达式为

-NT≤nT(t)≤NT

(5)

-NM≤nM(t)≤NM

(6)

式中：NT和NM分别为目标和拦截器的最大法向过载。

令Δv为拦截器速度与目标速度在弹目视线垂直方向上的分量之差，则有

Δv(t)=vMsinηM(t)-vTsinθ(t)

(7)

理想的拦截条件是Δv(t) = 0，此时，拦截器与目标在弹目视线垂直方向上的投影相同，拦截器可在无控条件下实现对非机动目标的拦截，即“零控拦截”。

2 TEW快速生成方法

2.1 TEW定义

在图1建立的坐标系中，定义

W={(x0,y0)∈R2:xM(0)=x0,yM(0)=y0,

xM(tf)=xT(tf),yM(tf)=yT(tf)}

(8)

式中：(x0,y0)为拦截器初始位置，tf为拦截时间，表征TEW的集合W由所有能够实现拦截的初始位置构成。需要注意，本文仅考虑由相对位置、速度、机动能力等决定的交战窗口，而实际交战中拦截器能否命中目标是由多种因素综合决定的。

拦截器的初始位置可由初始弹目距离和视线方向表示：

(9)

式中：r0=r(0)，θ0=θ(0)。

于是，求解TEW可转化为搜索(r0,θ0)的可行集。相对于高超声速目标，拦截器很难获得较大的速度优势，不适合采取尾追的拦截方式。因此，只需考虑θ0∈(-π/2, π/2)的情况。非故障情况下，拦截器在其左、右方向具有同样的机动性能。于是，窗口关于x轴对称，只需考虑θ0∈[0, π/2)的情况即可。

对于初始距离，约束表达式为

(10)

式中：rmin和rmax分别为末制导段最小和最大交战距离。

因此，(r0,θ0)可行集的搜索范围可缩小至

(11)

TEW的边界由三部分构成，分别为最小交战距离决定的内边界、最大交战距离决定的外边界，以及机动能力决定的侧向边界。因此，求解TEW边界的关键在于确定其侧向边界对应的r0与θ0的关系。

2.2 高超声速非机动目标拦截条件

考虑非机动目标，即目标法向过载为nT(t)=0，对式(1)进行积分得到

(12)

此时，目标只能在x轴上被命中。若拦截器初始速度前置角为0，则飞行轨迹如图2所示。图中，xM(t*)为拦截器与x轴第一次相交的位置，故yM(t*) = 0。

图2 初始速度前置角为0时的拦截轨迹示意图Fig.2 Trajectory of interceptor with zero initial lead angle

引理 1. 对于任意θ0∈(0, π/2)，当满足以下两个条件之一时，拦截器可以命中非机动目标:

条件1：Δv(0) ≤ 0且xM(t*) ≥xT(t*)；

条件2：Δv(0) ≥ 0且xM(t*) ≤xT(t*)。

证. 若满足条件1，则由xM(t*) ≥xT(t*)与yM(t*) =yT(t*) = 0，可得θ(t*) = 0且0 ≤ηM(t*) ≤ π。进而，代入式(7)得到

Δv(t*)=vMsinηM(t*)≥0

(13)

式(7)中，ηM(t*)和θ(t*)均随时间连续变化，故Δv(t)为连续函数。于是，由式(13)及条件1中的Δv(0) ≤ 0可知，存在t1∈[0,t*]，使得Δv(t1) = 0。根据“零控拦截”条件可知，拦截器可以命中非机动目标。此时，一条可行的拦截轨迹为：拦截器先以最大法向过载转弯，当满足Δv= 0时，再以零法向过载飞行，最后命中目标。需要注意的是，在满足条件1的情况下，可能存在无数条能够命中目标的拦截轨迹。例如，当Δv(0) = 0时，拦截器可以全程“零控”，也可以采取一定的机动。轨迹形式与制导方法相关，而本文研究的交战窗口只关注能够命中目标的拦截器初始阵位，故不对轨迹深入讨论。

同理可证，满足条件2时，存在t2∈[0,t*]，使得Δv(t2) = 0，故拦截器同样可以命中目标。

假设3. 对于高超声速目标拦截器，其最小转弯半径RM满足

(14)

定理 1. 对于任意θ0∈(0, π/2)，当Δv(0) ≤ 0时，若满足以下条件，则拦截器可以命中高超声速非机动目标：

(15)

式中：

(16)

证. 当Δv(0) ≤ 0时，拦截器轨迹类似图2中所描述，xM(t*)的取值由拦截器法向过载决定。当拦截器采用正的最大法向过载，即nM(t) =NM时，xM(t*)取值最大。若以航向角为自变量，式(2)可写为

(17)

取nM(t) =NM，积分式(17)可得

(18)

令yM(t*) = 0，则有

(19)

(20)

由式(14)可知上式成立，故ψM(t*)有解。考虑到ψM(t*)∈(π, 2π)，可解得

ψM(t*)=2π-arccosF1

(21)

代入式(18)，可得

(22)

另一方面，由于拦截器采用最大法向过载转弯，时间t*为

(23)

代入式(12)，可得

(24)

结合式(21)有

(25)

当xM(t*) ≥xT(t*)，即满足式(15)时，由引理1中条件1可知，拦截器可以命中非机动目标。

注1. 当拦截器转弯半径满足式(14)时，定理1也可作为其它低速目标的拦截条件。

定理2. 对于任意θ0∈(0, π/2)，当Δv(0) ≥ 0时，若满足以下条件，则拦截器可以命中高超声速非机动目标：

(26)

式中：

(27)

定理2与定理1的证明过程类似，这里不再赘述。

2.3 高超声速非机动目标TEW生成方法

定理1的证明中，拦截器采用正的最大法向过载，并得到xM(t*)最大值。当xT(t*)不超过xM(t*)最大值时，拦截器能够命中目标，故位置(r0,θ0)在TEW内。否则，拦截器无法在第一次与x轴相交时命中目标。这种情况下，拦截器只能调整航向并以尾追方式来拦截目标，由于调整航向过程中可能丢失目标，并且无较大速度优势下的尾追过程将耗费过长的时间，可以认为拦截失败，故位置(r0,θ0)不在TEW内。同理，定理2对应负的最大法向过载和xM(t*)的最小值。因此，定理1和定理2可用于判断方向θ0∈(0, π/2)上的位置r0是否在TEW内。而对于θ0=0，拦截器在目标正前方，显然可以命中。

理想的“无控拦截”期望Δv(0) = 0，根据式(7)得到理想的速度前置角为

(28)

式中：C=vM/vT为拦截器与目标的速度比。

将式(28)代入式(3)，得到理想的航向角为

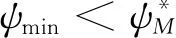
r0cosθ0=

(30)

由式(30)可解得位置(r0,θ0)处拦截器最小航向角ψmin。同理，可以求得最大航向角ψmax。事实上，由轨迹对称性可知，最大、最小航向角的轨迹在同一点(称之为H点)命中目标，且两条轨迹关于H点和初始点(称之为M点)构成的直线对称。因此，一旦得到最小航向角，可直接由下式计算最大航向角

ψmax=2ψMH-ψmin

(31)

式中：ψMH为M点指向H点的方向角。

在此基础上，考虑视场角约束，得到位置(r0,θ0)处的最小、最大航向角为

(32)

拦截器能够命中目标，当且仅当Ψmax(r0,θ0) ≥Ψmin(r0,θ0)，即满足

(33)

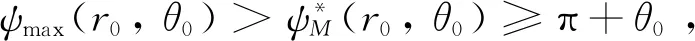
ψmin(r0,θ0)≤π+θ0+ηField

(34)

事实上，式(34)中的不等号条件对应TEW边界内部的点，而等号条件刚好对应TEW侧向边界。将式(34)取等并代入式(30)，有

(35)

式中：

(36)

因此，对于视线方向θ0，TEW侧向边界对应的初始距离r0可通过求解式(35)得到。

需要注意，虽然TEW内部的点都满足初始航向角Ψmax(r0,θ0)≥Ψmin(r0,θ0)，但是不同位置所允许的初始航向角变化范围不同。为此，定义航向角可控裕度

λ(r0,θ0)=Ψmax(r0,θ0)-Ψmin(r0,θ0)

(37)

于是，可将λ(r0,θ0) ≥ 0作为判断某一位置是否在TEW内的依据。不仅如此，λ(r0,θ0)也可以作为拦截器初始位置选择的依据，其值越大，意味着该位置处航向角的可控区间越大，拦截条件对扰动的敏感度也就越低。

2.4 高超声速机动目标TEW生成方法

临近空间高超声速目标通常采用倾斜转弯来实现侧向机动。在不发生倾侧角突然反号的情况下，其法向过载曲线变化缓慢，故末制导段的法向过载近似为常值。因此，计算高超声速机动目标的TEW时，可考虑以下三种情况：

情况1：目标的法向过载为nT(t) = 0；

情况2：目标的法向过载为nT(t) =NT；

情况3：目标的法向过载为nT(t) = -NT。

对于拦截器某一初始位置，若以上三种情况下的目标都可以被命中，则认为该位置在TEW内。情况1对应非机动目标，已在上一节研究，下面考虑情况2。此时，积分得到目标轨迹为

(38)

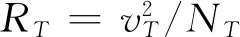
(39)

若目标在t=tf时刻被命中，则有

(40)

由上一节可知，拦截器最小航向角应满足

(41)

式中：

(42)

若令A= [ψM(tf)+ψmin]/2且B= [ψM(tf) -ψmin]/2，则式(41)可以写为

(43)

消除A可得

(44)

从式(44)中解出B之后，代入式(43)可以得到A，进而最小航向角为ψmin=A-B。而后，由式(31)可计算出最大航向角，再由式(32)得到考虑视场角约束的最小和最大航向角。对于情况3，可采用类似方法求解两个航向角，这里不再赘述。

(45)

式中：Λ(r0,θ0)为拦截机动目标时的航向角可控裕度，且

(46)

Λ(r0,θ0)≤λ(r0,θ0)

(47)

即拦截机动目标时，同一位置对应的可控裕度有所降低。这表明，相比于非机动目标，机动目标对拦截器的初始航向角提出了更为苛刻的要求。

3 仿真校验

在PC机(CPU: 3.4 GHz)上利用MATLAB进行仿真。结合临近空间高超声速目标运动特性，设定仿真条件如下：目标速度vT=2500 m/s；拦截器速度vM=3000 m/s，最大法向过载NM=6g，最大视场角ηField=30°；末制导段，拦截器与目标的最小交战距离rmin=5 km，最大交战距离rmax=50 km。

3.1 目标非机动情况下的TEW

在目标非机动情况下，TEW仿真结果如图3所示。图中，坐标原点(0, 0)为目标的初始位置，TEW的内外边界分别由最小和最大交战距离决定，侧向边界通过求解式(35)得到。P点为窗口内一点，坐标(40 km，10 km)。由P点出发，拦截器可以通过不同轨迹命中目标，其中，最大和最小初始航向角对应的轨迹如图4所示，两条轨迹分别采用正、负最大法向过载。

图3 拦截非机动目标的TEWFig.3 TEW for interception of non-maneuvering target

在P点处，拦截器最大和最小初始航向角分别为210.03°和201.39°，由式(37)可得，该位置可控裕度为8.64°。类似地，对所有位置求解最大和最小初始航向角，并计算可控裕度，得到的TEW如图5所示。离目标较远的位置，由于具有更充足的航向调整时间，对应的可控裕度相对较大。实际作战中，若可控裕度过小，则意味着该位置的航向角约束苛刻，不易作为末制导段的初始位置。假设作战所允许的最小可控裕度分别为3°、7°、10°，则相应的TEW如图6所示。不难发现，随着可控裕度要求的提升，TEW逐渐变小。最大可控裕度出现在(43 km, 24 km)和(43 km, -24 km)附近，这两个位置可以作为末制导段最佳初始阵位。

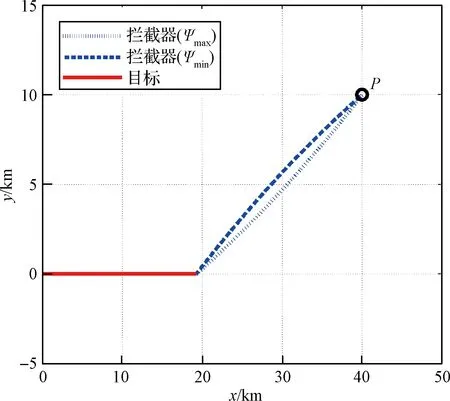
图4 拦截器最大与最小初始航向角对应的轨迹Fig.4 Interceptor’s trajectories with maximum and minimum heading angles

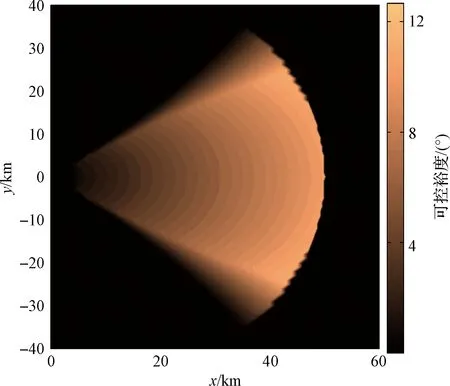
图5 带可控裕度的非机动目标TEWFig.5 TEW with controllable margin

需要指出，采用与文献[13]和[14]类似的数值方法也能得到高超声速目标的TEW。具体来说，就是给定初始位置后，在特定导引律下对拦截器和目标的飞行轨迹进行数值积分，再根据脱靶量判断该位置是否属于TEW，最后通过寻找某一视线方向上最近和最远位置得到TEW边界。相比而言，本文所提出的解析方法，直接由式(35)即可得到某一视线方向上的TEW边界，理论上求解更快。为进行仿真对比，假设拦截器采用比例导引律，在同样条件下用数值方法生成TEW。结果表明，两种方法得到的TEW边界几乎重合，验证了解析方法的正确性。此外，计算时间统计表明，解析方法生成一个TEW只需要0.2 s，而基于比例导引律的数值方法则需要770 s。可见，本文提出的解析方法在求解速度上优势明显，具有在线使用的潜能。

图6 不同最小可控裕度下的TEWFig.6 TEWs under various minimum controllable margins

3.2 目标机动情况下的TEW

针对机动目标，假定最大法向过载为NT= 2g。此时，TEW可综合nT(t) = 0g、nT(t) = 2g，以及nT(t) = -2g三种情况得到。对于nT(t) = 2g，拦截器在P点处的初始航向角可行区间为[199.99°，208.58°]，最大、最小初始航向角对应的拦截轨迹如图7所示。对于nT(t) = -2g，可行区间为[202.79°，211.49°]。结合nT(t) = 0g的结果可知，拦截机动目标的初始航向角可行区间为[202.79°，208.58°]，故可控裕度为5.79°，明显低于非机动目标时的可控裕度。

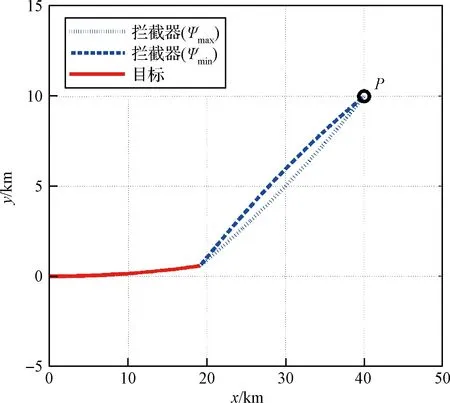
图7 目标法向过载nT (t) = 2 g对应的拦截轨迹Fig.7 Interception trajectories for target with nT (t) = 2 g

图8给出了NT= 2g情况下的TEW仿真结果。与图5对比可以看出，目标最大法向过载提升后，TEW的覆盖范围略有减小，且TEW内的同一位置的可控裕度也减小，但最大可控裕度对应的位置不发生明显改变。这意味着，目标的机动能力的提升会使得拦截器初始航向角约束更为苛刻，但对最佳初始位置影响不大。

图8 目标最大法向过载NT = 2 g情况下的TEWFig.8 TEW for target with NT = 2 g

3.3 TEW影响因素分析

TEW外边界和内边界分别由最大和最小交战距离决定，而侧向边界受到拦截器速度、最大视场角、最大法向过载等因素的影响。以非机动目标为例，考虑拦截器速度降低至2500 m/s和提升至3500 m/s两种情况，相应的TEW如图9所示。随着拦截器速度的提升，TEW的覆盖范围逐渐增大，但由于速度增大会影响转弯能力，窗口同一位置对应的可控裕度有所降低。图10比较了拦截器不同最大视场角对应的TEW。视场角的增大会使得TEW覆盖范围增大，但对于大部分位置(接近边界的位置除外)，其可控裕度几乎不变。图11比较了拦截器最大法向过载分别为5g、6g、7g时的TEW。可以看出，最大法向过载增大后，TEW覆盖范围变化不大，但内部位置对应的可控裕度明显提升。综上，拦截器速度、最大视场角、最大法向过载的改变会对TEW产生不同影响。提升速度和最大视场角都可以增大TEW的覆盖范围，而降低速度或提升最大法向过载可以增大TEW内位置的可控裕度。

本文提出的TEW生成方法基于图1建立的坐标系，坐标原点由目标的初始位置和航向角决定。实际作战中，拦截器无法准确地获得目标运动信息。初始位置偏差会使得TEW产生位移，而初始航向角偏差会使得TEW产生转动。考虑目标信息xT(0),yT(0)和ψT(0)的测量误差，假设三者都服从零均值高斯分布，且三倍标准差分别为100 m、100 m和1°。随机生成100组测量误差，计算出相应的TEW边界如图12所示。结果表明，测量信息存在误差情况下，所提出的方法依然有效。同时，鉴于测量误差产生的影响并不大，可以基于标称条件计算TEW。

图9 拦截器不同速度情况下的TEWFig.9 TEWs for interceptor with various velocities

图10 拦截器不同最大视场角情况下的TEWFig.10 TEWs for interceptor with various maximum field angles

图11 拦截器不同最大法向过载情况下的TEWFig.11 TEWs for interceptor with various maximum normal accelerations

图12 考虑目标信息测量误差的TEWFig.12 TEWs under measurement errors of target

4 结 论

本文针对高超声速目标拦截问题，研究了末段交战窗口，建立了解析形式的拦截条件，提出了非机动目标和机动目标末段交战窗口的解析求解方法。仿真表明，解析方法得到的窗口边界与传统数值方法的结果一致，但求解时间大幅减小，具有在线使用的潜力。分析了影响末段交战窗口的主要因素，并发现增大窗口覆盖范围可通过提升拦截器速度和视场角实现，而增大窗口内位置的可控裕度可通过降低速度或提升最大法向过载实现。此外，所提出的窗口生成方法对目标信息的测量误差具有较好的适应性，当存在一定的测量误差时，窗口变化不大。本文所建立的末段交战窗口，主要针对高超声速目标的二维拦截问题，后续研究中可基于三维弹目相对运动建立相应的拦截条件，进而得到三维交战窗口。