大气密度对运载火箭飞行的qαmax精度影响及建模分析

程胡华，王益柏，蔡其发，赵 亮

(1. 63729部队，太原030027；2. 61741部队，北京 100094；3. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京 100029)

0 引 言

近年来，中国在航天领域取得一系列丰硕成果，运载火箭作为航天技术领域里的核心之一，其内部结构非常复杂，并汇聚了无数尖端技术，为持续提高其完成任务的成功率，大量科学家对运载火箭结构特征、飞行控制等方面开展了一系列研究[1-4]，并取得了丰富的成果；在发射之前，除确保运载火箭本身满足发射、飞行条件外，还需考虑大气环境的影响，目前主要关注高空风对运载火箭飞行的影响[5-13]，例如，程镇煌[5]通过全面叙述大型火箭风载试验的各种问题，指出火箭设计必须经过靶场风载试验和高空风载试验，测出火箭各舱段载荷和仪器舱处风激振幅等，准确确定各种设备的适应能力；余梦伦[7]指出发现高空风引起的气流攻角对火箭飞行中的气动载荷和飞行环境有较大的影响，这种影响有时可造成火箭飞行失败。

目前，在定量分析大气环境对运载火箭飞行影响(即qαmax)的计算程序中，除了需要大气高空风参数外，还需要大气密度参数，但程序中的大气密度参数通常采用参考大气密度，而非发射场零日的真实大气密度，针对大气密度对运载火箭或其它飞行器飞行的影响，广大科学工作者已开展了一系列工作，并取得大量有意义成果[14-23]，黄世勇和闻悦[14]指出大气密度对飞行器的安全及返回有非常重要影响，李健等[20]研究发现大气密度是建立飞行动力学模型的重要参数，不同的大气密度模型对弹道终点高度、最大过载、最大热流等参数影响明显；程旋等[21]指出飞行器的气动力和气动力矩都是大气密度的函数，大气密度的变化直接影响到飞行状态下飞行器的受力，对飞行器的姿态影响显著，引起攻角、侧滑角、偏航角等角度的变化，导致再入飞行器偏离预定轨迹；因此，大量科技工作者针对大气密度开展一系列研究工作[24-27]。

获取参考大气密度的参考大气模型有CIRA系列、MSIS系列等，由于大气密度受来自太阳辐射及大气波动的共同影响，变化十分复杂，人们至今尚未完全掌握其变化的物理机制，导致已有的参考大气模型精度不高[19,24,28]，因此，在采用参考大气密度定量计算大气环境对运载火箭飞行的qαmax时，由于参考大气密度与真实大气密度之间存在偏差，但针对其偏差对运载火箭飞行的qαmax精度特征研究尚未见相关文献，考虑到目前计算程序仍采用参考大气密度，本文利用2017年8月1日-2019年7月31日晋西北地区探空资料，分别利用MSIS00模式参考大气密度、真实大气密度计算某型运载火箭飞行时的qαmax，一方面对MSIS00模式参考大气密度与真实大气密度之间的差异特征进行研究，另一方面对它们之间的qαmax差异进行统计，最后，利用多元线性回归、BP神经网络方法对基于MSIS00模式参考大气密度得到的qαmax建立订正模型，并对订正效果进行检验。

1 资料及方法

1.1 探空资料

探空资料为晋西北地区每日08时(北京时，下同)，时间长度为2017年8月1日-2019年7月31日，所需气象要素为高度、气压、风速、风向、温度和相对湿度，单位分别为m，hPa，m·s-1，(°)，℃和%，考虑到qαmax值常出现在16 km高度以下，故选取探空资料的几何高度范围为0～20000 m，其中，0～10000 m高度范围内间隔为200 m，10000～20000 m高度范围内间隔为500 m。

1.2 计算真实大气密度

利用高垂直分辨率探空资料计算真实大气密度，对于湿空气，利用温度、相对湿度、气压可计算大气密度，计算步骤如下[29]：

1)计算饱和水汽压

(1)

式中：T为温度。

2)计算水汽压

e=10-2RH·es

(2)

式中：RH为相对湿度。

3)计算比湿

(3)

式中：p为气压。

4)计算湿空气的比气体常数

Rv=Rd(1+0.608q)

(4)

式中：Rd为干空气的比气体常数，数值为287.05，单位为J/(kg·K)。

5)利用湿空气的状态方程，可计算湿空气大气密度

(5)

1.3 MSIS参考大气模式

MSIS(Mass Spectrometer and Incoherent Scatter empirical model)大气模式最初版本是由美国国家航空航天局空间飞行中心编制的经验大气预报模式，通过利用多颗卫星质谱计所测得的成分资料和非相干散射雷达探测资料而建立，目前MSIS00是该系列模式的较新版本[30]，其利用了更新、更多的雷达、卫星和火箭资料，是当今国际上广泛使用的参考大气模式[31-35]，MSIS00模式的适用高度范围为地面至高层大气，可给出不同高度层的大气温度、大气密度及成分结构。

1.4 统计方法

以真实大气密度为基准，通过计算参考大气密度与真实大气密度之间的偏差、相对偏差和偏差区间占有率，反映参考大气密度误差特征，其相应的计算公式如下：

(6)

(7)

式中：Bias为偏差，Rerr为相对偏差，n为样本数，x和y分别代表参考大气密度与真实大气密度。

文中的偏差区间占有率计算式定义如下：

(8)

式中：若xi-yi<-N结果成立，则定义xi-yi<-N的值为1，否则值为0;该定义同样适用于表达式-N≤xi-yi≤N和xi-yi>N。

2 密度差异特征

2.1 平均差异特征

在2017年8月1日-2019年7月31日，参考大气密度与真实大气密度之间的偏差、相对偏差随高度变化特征如图1所示，偏差随高度增加呈现正值、负值的交替变化特征(见图1(a))，其正偏差值主要位于高度2.00～7.60 km，负偏差值主要位于高度11.40～19.90 km，整个高度范围内的值范围为-0.0083 kg·m-3(14.90 km)～0.0065 kg·m-3(4.20 km)，平均值为5.2843×10-4kg·m-3；类似偏差(见图1(a))，相对偏差随高度增加同样呈现正值、负值的交替变化特征(见图1(b))，但高层的相对偏差值明显大于低层，其正相对偏差值主要位于高度2.00～7.60 km，负相对偏差主要位于高度11.40～19.90 km，整个高度范围内的值范围为-4.2142%(15.90 km)～5.2210%(21.40 km)，平均值为-0.3063%；对照图1(a)与图1(b)可知，虽然偏差、相对偏差随高度变化趋势基本一致，但大值区所处的高度层存在一定差异，例如，偏差极大值(0.0065 kg·m-3)、极小值(-0.0083 kg·m-3)分别位于4.20 km，14.90 km，而相对偏差极大值(5.2210%)、极小值(-4.2142%)分别位于21.40 km和15.90 km。

图1 在2017年8月1日-2019年7月31日，参考大气密度与真实大气密度之间的密度偏差、密度相对偏差随高度变化特征Fig.1 The altitude variations of deviations and relative deviations between the reference atmospheric density and the true atmospheric density from August 1, 2017 to July 31, 2019

2.2 年内差异特征

在2017年8月1日-2019年7月31日，参考大气密度与真实大气密度之间偏差、相对偏差的年内—高度变化特征如图2所示；对于年内变化特征，在低层，偏差值呈现负值、正值、负值变化特征，其正偏差极大值出现在7月，而在高层则表现为正值、负值、正值变化特征，其负偏差极大值出现在8月(见图2(a))；对于高度变化特征，1-3月、11-12月偏差随高度增加呈现出由负偏差向正偏差转变过程，而在4-10月则表现为正偏差向负偏差转变过程；在图2(a)中，低层(2.0～4.0 km)的6-8月存在一个正偏差大值区，高层(13～17 km)的7-9月存在一个负偏差大值区，最小值为-0.0538 kg·m-3(12月的2.00 km)，最大值为0.0558 kg·m-3(7月的2.0 km)，平均值为5.3219×10-4kg·m-3；类似偏差(见图2(a))，相对偏差同样存在明显的年内变化及随高度变化特征(见图2(b))，对于年内变化特征，低层(10 km以下)呈现出负值、正值、负值的变化特征，而高层(10 km以上)则表现为正值、负值、正值的变化特征；对于高度变化特征，1-3月、11-12月随高度增加呈现出负相对偏差向正相对偏差转变特征，而4-10月随高度增加呈现出正相对偏差向负相对偏差转变，图2(b)中的负相对偏差最大值为-13.2699%(8月的15.90 km)，正相对偏差最大值为10.1708%(12月的21.40 km)，平均值为-0.3046%。

图2 2017年8月1日-2019月7月31日，参考大气密度与真实大气密度之间的密度偏差、密度相对偏差随年内—高度变化特征Fig.2 The time-altitude cross section of deviations and relative deviations between the reference atmospheric density and the true atmospheric density from August 1, 2017 to July 31, 2019

2.3 季节差异特征

在2017年8月1日-2019年7月31日，不同季节参考大气密度与真实大气密度之间的偏差、相对偏差随高度变化特征如图3所示，偏差、相对偏差随高度变化特征与季节有关，春、夏、秋季的大气密度偏差在低层以正值为主，偏差值由大到小分别为夏季、春季、秋季，在高层以负值为主，偏差值由大到小分别为夏季、秋季、春季；而冬季的大气密度偏差在低层以负值为主，在高层以正值为主(见图3(a))，在整个高度范围内，春、夏、秋、冬季的大气密度偏差范围分别为-0.0055 kg·m-3(11.90 km)～0.0120 kg·m-3(2.00 km)，-0.0234 kg·m-3(14.90 km)～0.0515 kg·m-3(2.00 km)，-0.0097 kg·m-3(14.90 km)～0.0047 kg·m-3(4.20 km)，-0.0505 kg·m-3(2.00 km)～0.0134 kg·m-3(11.40 km)，平均值分别为4.8702×10-4kg·m-3，0.0083 kg·m-3，-0.0013 kg·m-3，-0.0054 kg·m-3；类似图3(a)，相对偏差随高度变化特征同样与季节密切相关(见图3(b))，其中，春、夏、秋季的大气密度相对偏差在低层以正值为主，相对偏差值由大到小分别为夏季、春季、秋季，在高层以负值为主，相对偏差值由大到小分别为夏季、秋季、春季；而冬季的大气密度相对偏差在低层以负值为主、高层以正值为主，在整个高度范围内，春、夏、秋、冬季的大气密度相对偏差范围分别为-3.0923%(17.90 km)～5.9970%(21.40 km)，-11.6516%(15.90 km)～5.4388%(2.00 km)，-4.7972%(15.90 km)～5.2188%(21.40 km)，-4.7440%(2.00 km)～10.0290%(21.40 km),平均值分别为-0.2805%，-0.7126%，-0.7011%，0.4637%，对照图3(a)和图3(b)及上述分析可知，虽然大气密度偏差与相对偏差随高度变化趋势基本一致，但出现极大值、极小值的高度层存在差异，且在整个高度层，春季和夏季的平均偏差为正值、秋季和冬季的平均偏差为负值；而春、夏、秋季的相对偏差均为负值，冬季为正值。

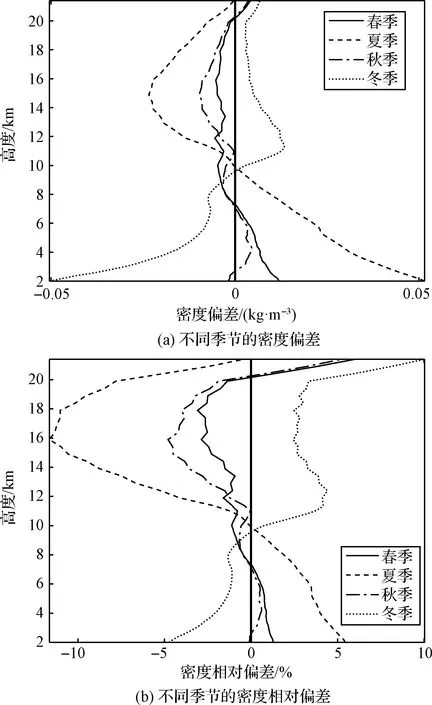
图3 2017年8月1日-2019年7月31日，不同季节参考大气密度与真实大气密度之间的密度偏差、密度相对偏差随高度变化特征Fig.3 The altitude variations of deviations and relative deviations between the reference atmospheric density and the true atmospheric density from August 1, 2017 to July 31, 2019 in different seasons

2.4 平均年内变化特征

在2017年8月1日-2019年7月31日的1-12月，整个高度层内的平均大气密度偏差呈现“∧”字符变化特征(见图4(a))，其中，1-3月、10-12月为负偏差，4-9月为正偏差，图4(a)中的值范围为-0.0060 kg·m-3(11月)～0.0099 kg·m-3(7月)，平均值为5.3219×10-4kg·m-3；整个高度层内的平均大气密度相对偏差年内变化特征如图4(b)所示，与图4(a)基本相反(从图2(a)与图2(b)之间的高层、低层差异可以解释)，图4(b)中的1-3月和12月为正相对偏差、4-11月为负相对偏差，其值范围为-0.9569%(8月)～0.7225%(2月)，平均值为-0.3046%。

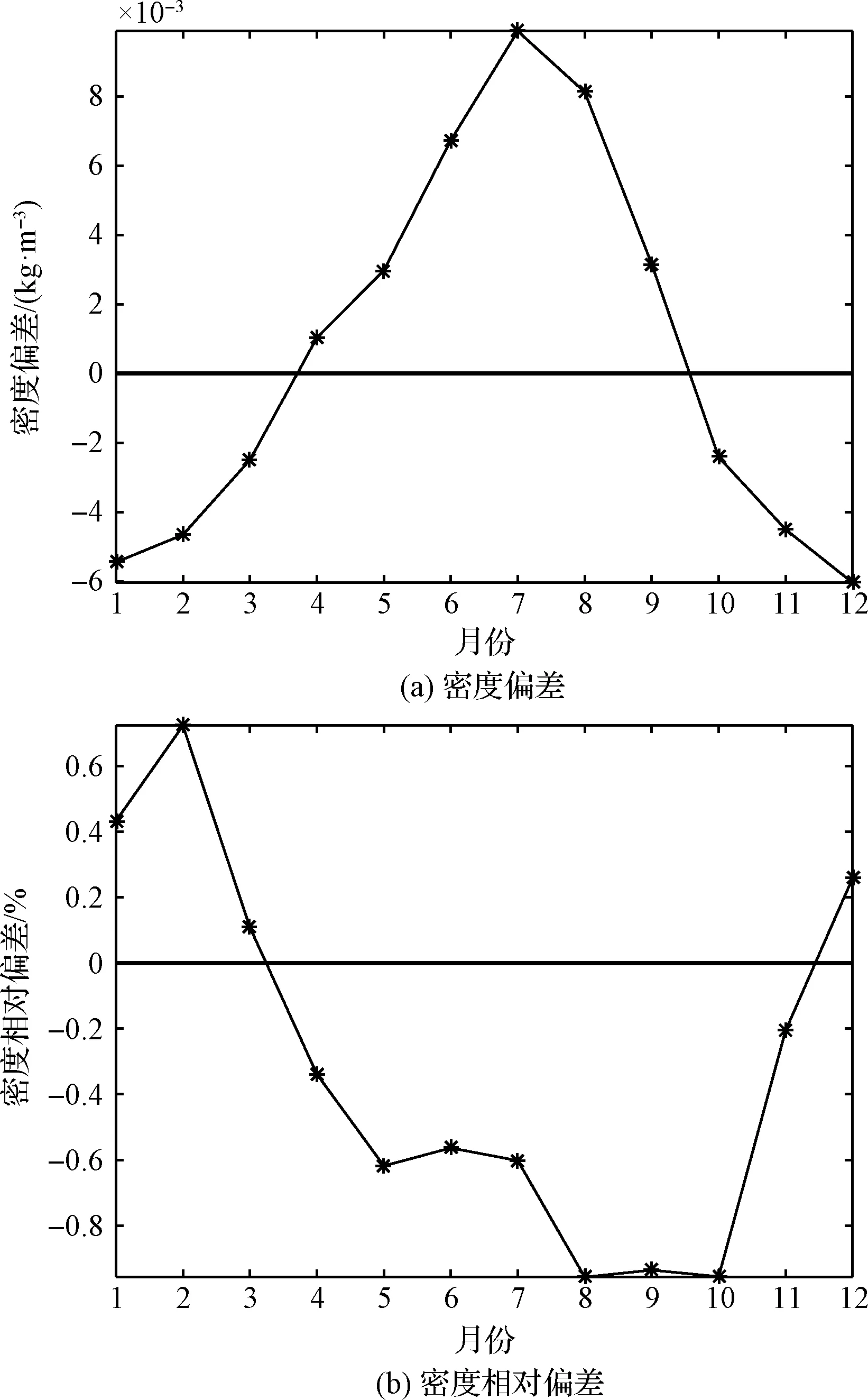
图4 2017年8月1日-2019年7月31日，整个高度层内参考大气密度与真实大气密度之间的密度偏差、密度相对偏差年内变化特征Fig.4 The annual variation of deviations and relative deviations between the reference atmospheric density and the true atmospheric density within the entire height from August 1, 2017 to July 31, 2019

3 qαmax差异特征

3.1 qαmax差异统计

通过上述研究发现，参考大气密度与真实大气密度之间的差异特征与高度、季节均有密切关系，在2017年8月1日-2019年7月31日，参考大气密度与真实大气密度之间的qαmax偏差特征如图5所示，qαmax偏差呈现“M”字型变化特征(见图5(a)，图中粗虚线分别对应+100 Pa·rad，-100 Pa·rad，图5(a)中的值范围为-217.1721～219.0648 Pa·rad，平均值为-9.4684 Pa·rad，其中，正偏差超过100 Pa·rad的样本数有24个，负偏差超过-100 Pa·rad的样本数有49个；qαmax偏差在不同区间范围内的占有率特征如图5(b)所示，沿横坐标轴方向呈现增大、减小的变化趋势，其中，qαmax偏差在(-20, 0]范围内占有率最大(20.4110%)，在[0，20)范围内占有率为次大值(16.0274%)，在(-∞， -100]、(100， +∞)范围内的占有率分别为6.7123%，3.2877%；类似平均大气密度偏差存在明显的年内变化特征(见图4(a))，qαmax偏差同样具有明显的年内变化特征(见图5(c))，但变化特征与图4(a)相反，图5(c)中的qαmax偏差在1-3月、11-12月为正偏差，4-10月为负偏差，在1-12月的值范围为-51.3659 Pa·rad(6月)～46.3820 Pa·rad(1月)，平均值为-9.5690 Pa·rad，qαmax偏差同样与季节有关(见图5(d))，其中，春、夏、秋季均为负偏差，冬季为正偏差，负偏差最大值出现在夏季(-42.5615 Pa·rad)，正偏差最大值出现在冬季(37.8531 Pa·rad)。

3.2 qαmax偏差超过100 Pa·rad

参考大气密度与真实大气密度之间的qαmax偏差超过100 Pa·rad时，其分布特征如图6所示，其中，有24个样本的qαmax偏差超过100 Pa·rad(见图6(a))，有49个样本的qαmax偏差超过-100 Pa·rad(见图6(b))，在图6(a)中，qαmax偏差值范围为101.1910～219.0648 Pa·rad，其中，基于参考大气密度得到的qαmax值范围为1.8522×103～4.7914×103Pa·rad，而基于真实大气密度得到的qαmax值范围为1.7337×103～4.6090×103Pa·rad；在图6(b)中，qαmax偏差值范围为-101.4770～-217.1721Pa·rad，其中，基于参考大气密度得到的qαmax值范围为873.2646～2.8181×103Pa·rad，而基于真实大气密度得到的qαmax值范围为982.6712～3.0027×103Pa·rad。

在2017年8月1日-2019年7月31日，qαmax偏差值超过100 Pa·rad时，对应的风场、大气密度偏差随高度变化特征如图7所示。从图7(a)可以看出，虽然qαmax偏差≤-100、qαmax偏差≥100对应的风场随高度变化趋势基本一致，且极大值出现在基本相同的高度层(12 km左右)、极小值均出现在2 km，但qαmax偏差≥100对应的风速在各高度层均大于相应的qαmax偏差≤-100，在整个高度范围内，qαmax偏差≤-100，qαmax偏差≥100对应的风速范围分别为5.9592 m·s-1(2.8 km)～40.0294 m·s-1(12.90 km)，7.2083 m·s-1(2.0 km)～58.8748 m·s-1(11.90 km)，平均值分别为18.0332 m·s-1，33.8605 m·s-1，qαmax偏差≤-100、qαmax偏差≥100对应的大气密度偏差随高度变化特征存在明显差异(见图7(b))，其中，qαmax偏差≤-100对应大气密度偏差随高度增加呈现正偏差向负偏差转变，而相应的qαmax偏差≥100为负偏差向正偏差转变，即两者表现为相反的变化特征，在整个高度范围内，qαmax偏差≤-100，qαmax偏差≥100对应的大气密度偏差范围分别为-0.0217 kg·m-3(13.90 km)～0.0386 kg·m-3(2.0 km)，-0.0539 kg·m-3(2.0 km)～0.0178 kg·m-3(11.0 km)，平均值分别为0.0058 kg·m-3，-0.0052 kg·m-3。

图5 2017年8月1日-2019年7月31日，qαmax偏差变化及其在不同区间范围内的占有率、年内变化和季节变化特征Fig.5 The change characteristics, percentages in different ranges, annual variation and seasonal variation of qαmax deviation from August 1, 2017 to July 31, 2019

图6 在qαmax偏差≥100 Pa·rad、qαmax偏差≤-100 Pa·rad时，基于真实大气密度与参考大气密度计算得到的qαmax值变化特征Fig.6 Under the qαmaxdeviation≥100 Pa·rad, qαmax deviation≤-100 Pa·rad conditions, the variation characteristics of qαmax value calculated based on true atmospheric density and reference atmospheric density

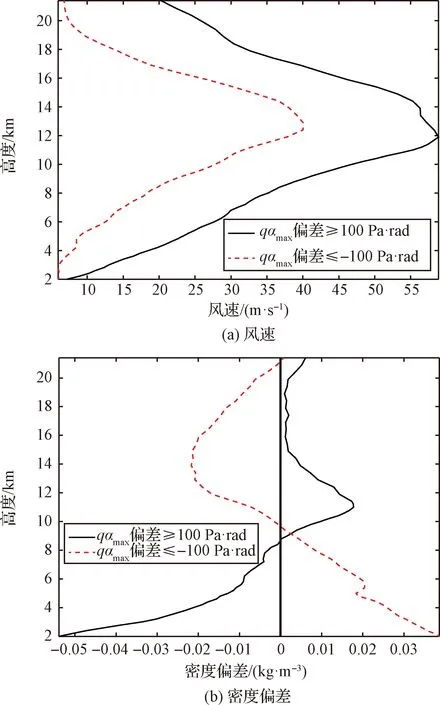
图7 qαmax偏差值超过100 Pa·rad时，风速、密度偏差随高度变化特征Fig.7 The altitude variations of upper wind speed, atmospheric density deviation when the value of qαmaxdeviation exceeds 100 Pa·rad

4 建 模

基于目前计算大气环境对运载火箭飞行的qαmax程序包中，大气密度为参考大气密度、而非真实大气密度，通过上述研究可以看出，由于参考大气密度与真实大气密度之间存在差异，导致该程序包计算得到的qαmax与真实值之间存在差异，偏差最大值超过200 Pa·rad，为减小运载火箭飞行的风险，一方面，强烈建议采用真实大气密度代替程度包中的参考大气密度，另一方面，可考虑采用多元线性回归、BP神经网络等建模方法建立订正模型，本文采用常用的多元线性回归方法、BP神经网络方法建立订正模型，并对订正模型的效果进行检验。

4.1 建模思想

基于2017年8月1日-2019年7月31日，一共730个样本，其中:1)前600个样本作为训练样本，后130个样本作为检验样本；2)基于参考大气密度计算得到qαmax对应的运载火箭飞行高度h，获取0～h高度范围内的纬向风、经向风、参考大气密度平均值，分别记为umean，vmean，ρmean；3)日期以天数表示，其中，1月1日为1，1月31日为31，…，记为d；4)计算参考大气密度与真实大气密度之间的qαmax偏差；5)对2017年8月1日-2019年7月31日(共730个样本)的h，umean，vmean，ρmean，d归一化处理，即将数值转换为[-1,1]范围内；6)针对前600个样本，利用多元线性回归、BP神经网络方法对h，umean，vmean，ρmean，d与qαmax偏差之间建立模型；7)基于已建立好的订正模型，利用后130个样本的h，umean，vmean，ρmean，d参数，得到订正模型的qαmax偏差值(记为Dqαmax)，Dqαmax与参考大气密度计算得到的qαmax(记为Rqαmax)之和，即为所需要的结果。

基于参考大气密度、真实大气密度得到的qαmax分别记为Rqαmax，Tqαmax，BP神经网络、多元线性回归方法建立订正模型得到的qαmax，分别记为Bqαmax，Mqαmax；本文基于多元线性回归方法建立的模型如下：

49.89umean-40.42vmean-83.18ρmean-9.94d-

103.56h-23.08=Dqαmax

(9)

Mqαmax=Rqαmax-Dqαmax

(10)

在式(9)～(10)中，umean，vmean，ρmean，d和h的变量意义与前面描述一致，为后130个样本的已知量，Rqαmax为基于参考大气密度得到的后130个样本qαmax；利用式(9)可计算得到Dqαmax，Dqαmax反映了Rqαmax与基于多元线性回归方法得到Mqαmax之间的偏差；利用式(10)得到的Mqαmax，即为基于多元线性回归方法建立模型得到的qαmax订正值。

本文使用的BP神经网络方法，是采用MATLAB软件自带的神经网络工具箱进行建模，同样先得到Dqαmax，其中，Dqαmax反映了Rqαmax与基于BP神经网络方法得到Bqαmax之间的偏差；利用式(11)即可得到基于BP神经网络方法的Bqαmax，即

Bqαmax=Rqαmax-Dqαmax

(11)

式中：Rqαmax为基于参考大气密度得到的后130个样本qαmax。

记Rqαmax，Bqαmax，Mqαmax与Tqαmax之间的偏差分别为RqαmaxDev，BqαmaxDev，MqαmaxDev，下面利用数理统计方法对BP神经网络、多元线性回归方法建立的订正模型效果进行检验。

4.2 模型检验

在后130个样本中，RqαmaxDev，BqαmaxDev，MqαmaxDev的变化特征及在不同区间范围占有率分布特征如图8所示，从图8(a)可以看出，通过对参考大气密度的结果进行BP神经网络、多元线性回归建模订正处理，所得到的qαmax偏差明显减小，在图8(a)中，RqαmaxDev，BqαmaxDev，MqαmaxDev的值范围分别为-201.6939～122.1358 Pa·rad，-75.9311～39.4346 Pa·rad，-52.6029～60.1846 Pa·rad；RqαmaxDev，BqαmaxDev，MqαmaxDev在不同区间范围内的占有率存在明显差异(见图8(b))，其中，RqαmaxDev在区间(-20，0]占有率最高(19.2308%)，在区间(0，20]占有率次高(15.3846%)，BqαmaxDev在区间(-20，0]占有率最高(31.5385%)，在区间(-40，-20]占有率次高(27.6923%)，MqαmaxDev在区间(-40，-20]占有率最高(27.6923%)，在区间(0，20]占有率次高(26.9231%)，从图8(b)还可以看出，RqαmaxDev，BqαmaxDev，MqαmaxDev占有率为0.00%的区间范围也存在明显差异，RqαmaxDev在区间(60,80]占有率为0.00%，BqαmaxDev在区间(-∞，-100]，(-100，-80]，(40，60]，(60，80]，(80，100]，(100，∞]内的占有率均为0.00%，MqαmaxDev在区间(-∞，-100]，(-100，-80]，(-80，-60]，(80，100]，(100，∞]内的占有率均为0.00%。Rqαmax，Bqαmax，Mqαmax与Tqαmax之间的平均偏差、平均绝对差、平均相对偏差、平均标准差及相关系数统计结果见表1。

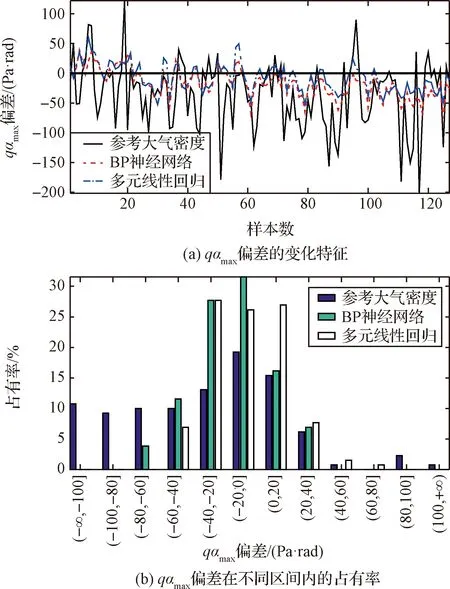
图8 RqαmaxDev，BqαmaxDev，MqαmaxDev的变化及其在不同区间范围占有率分布特征Fig.8 The variation characteristics, and percentages in different ranges of RqαmaxDev，BqαmaxDev，MqαmaxDev

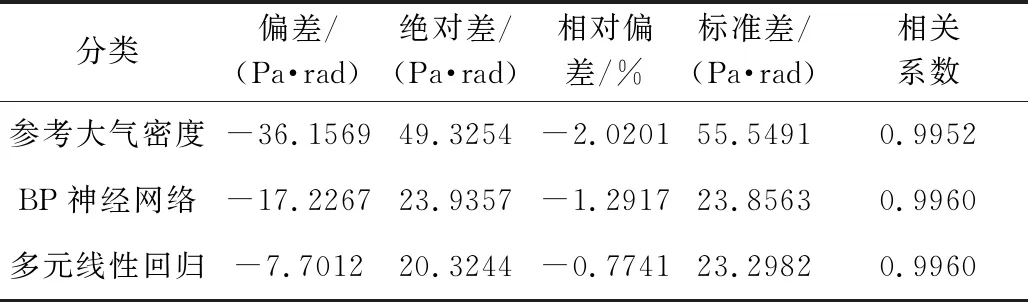
表1 Rqαmax，Bqαmax，Mqαmax与Tqαmax之间的数理统计特征Table 1 The mathematical statistics results between Rqαmax，Bqαmax，Mqαmax and Tqαmax

5 结 论

运载火箭飞行前，需确定发射场大气环境对运载火箭飞行的影响，若计算得到的qαmax超过阈值，则发射推迟；在计算qαmax的程序中，所用的大气密度通常是参考大气密度，而非发射场零日的真实大气密度，目前针对参考大气密度对qαmax精度的影响研究较少，本文以2017年8月1日-2019年7月31日高垂直分辨率探空资料为例，分析参考大气密度与真实大气密度以及它们计算得到某型运载火箭飞行qαmax之间的差异特征，最后建立订正模型，得到主要结论如下：

1)密度偏差、相对偏差随高度增加而呈现正值、负值的交替变化特征，整个高度层内的平均大气密度偏差、相对偏差具有明显年内变化特征，其中，偏差值在1-3月、10-12月为负值，4-9月为正值，值范围为-0.0060 kg·m-3(11月)～0.0099 kg·m-3(7月)，相对偏差在4-11月为负值，1-3月、12月为正值，值范围为-0.9569%(8月)～0.7225%(2月)。

2)参考大气密度与真实大气密度之间的qαmax偏差随时间变化呈现“M”字型特征，其值范围为-217.1721～219.0648 Pa·rad，平均值为-9.4684 Pa·rad；qαmax偏差值在不同区间范围内占有率存在较明显差异，其最大占有率(20.4110%)位于(-20,0]区间范围。

3)参考大气密度与真实大气密度之间的qαmax偏差，具有明显的年内、季节变化特征；其中，1-3月、11-12月为正偏差，4-10月为负偏差，值范围为-51.3659 Pa·rad(6月)～46.3820 Pa·rad(1月)，春、夏、秋季为负偏差，冬季为正偏差，值范围为-42.5615 Pa·rad(夏季)～37.8531 Pa·rad(冬季)。

4)通过对qαmax偏差≥100 Pa·rad、qαmax偏差≤-100 Pa·rad对应的风场、大气密度偏差进行对比发现，qαmax偏差≥100 Pa·rad对应的风速在各高度层均明显偏大、大气密度偏差随高度增加呈现负值向正值转变，而qαmax偏差≤-100 Pa·rad对应的风速在各高度层均偏小、且大气密度偏差为正值向负值转变。

5)基于参考大气密度得到的qαmax偏差，通过利用多元线性回归、BP神经网络方法建立模型进行订正，结果表明均能够较好地提高qαmax精度，且多元线性回归建立的模型改进效果更好；与参考大气密度得到的qαmax相比，多元线性回归、BP神经网络方法建立模型得到的qαmax偏差由-36.1569 Pa·rad减小到-7.7012 Pa·rad，-17.2267 Pa·rad，绝对差由49.3254 Pa·rad减小到20.3244 Pa·rad，23.9357 Pa·rad，相对偏差由-2.0201%减小到-0.7741%，-1.2917%，标准差由55.5491 Pa·rad减小到23.2982 Pa·rad，23.8563 Pa·rad，相关系数由0.9952提高到0.9960，0.9960。

通过上述研究结果可以看出，由于参考大气密度与真实大气密度之间的偏差存在年内、季节变化特征，导致所计算得到的qαmax偏差同样存在较明显年内、季节变化，且正、负偏差最大值均超过200 Pa·rad；考虑到目前计算程序中所用的大气密度通常是参考大气密度，而非发射场零日真实大气密度，若程序计算得到的qαmax接近阈值，则此时真实的qαmax可能超过阈值，导致运载火箭飞行存在重大风险。虽然采用多元线性回归或BP神经网络建立订正模型可以提高qαmax精度，但同样存在一定风险，因此，在分析大气环境对运载火箭飞行的影响时，最好采用发射场零日真实大气密度代替参考大气密度，从而得到运载火箭飞行时真实的qαmax，进一步提高运载火箭飞行的保障能力，避免出现重大事故；考虑到火箭发射前，需提前几天确定发射场区发射零日是否满足发射条件，然而，此时没有未来几天的大气密度实况资料、且考虑大气密度与多种因素有关(温度、相对湿度等)，因此，通过建立大气密度预报模型，获取更接近真实大气密度的大气密度预报值，代替计算程序中的参考大气密度，可能是后期进一步提高精度的研究方向。