平板缺陷对单一模态lamb 波传播的影响

卢鸿宇

（天津大学，天津 300350）

1 有限元仿真

本文使用有限元软件COMSOL 对平板中的lamb 波进行有限元仿真研究，研究不同类型的缺陷对lamb 波传播的影响。

1.1 材料参数的赋值

本文对lamb 波在钢板材料内的性质进行研究，于是，根据一般钢材的材料性质设置参数（表1）。

表1

1.2 物理场的设置

根据不同模式的lamb 波的质点位移特点给予相应位移边界条件，进而激励出不同类型的lamb 波。

位移激励信号形式采用余弦周期函数，用汉宁窗函数截取信号的前五个周期进行激励。当材料厚度为1mm 时，我们可以从频散曲线中确定某一个频率范围，在此频率范围内只有一种模态的lamb 波。

使用1.98MHz 以前频率激励，就能得到单一模态的lamb 波。

除了上述所给边界条件外，剩余边都为自由边。在特殊情况下为减少不同类型lamb 间的互相影响，应在平板的尾部加上低反射边界条件以减少边界反射波的影响。

1.3 计算域和计算时间的确定（表2）

表2

在确定好各项设置后即可进行有限元计算。

2 后处理及分析

2.1 lamb 波在无缺陷板中的传播

以板的几何中心为原点设置两个信号接收点，两信号接收点间相距100mm。

作为示例下面分别给出了两种类型的lamb 波在板中传播时信号接收点所得到的信号情况。

根据信号叠加图像可以计算出图1 中波群速度为3184.71m/s, 图2 中波群速度为5263.16m/s。根据理论公式可得出材料中S0模态和A0模态波速分别为5814.91m/s 和3244.36m/s。因此可以确定图1 中描述的是A0模态lamb 波传播情况，图2 则描述S0模态lamb 波传播情况。

2.2 单一模态lamb 波在有缺陷板中的传播

2.2.1 单一模态lamb 波通过对称缺陷

在进行S0模态lamb 波受外部对称缺陷影响的仿真分析时，S0模态lamb 波在经过边界反射后不再具有典型的波包结构。由于本文研究的是缺陷对lamb 波的影响，而通过边界反射的lamb 波不在本文研究范围内，所以本次在板右边界上给予低反射边界条件以降低反射lamb 波的影响。

图1

图2

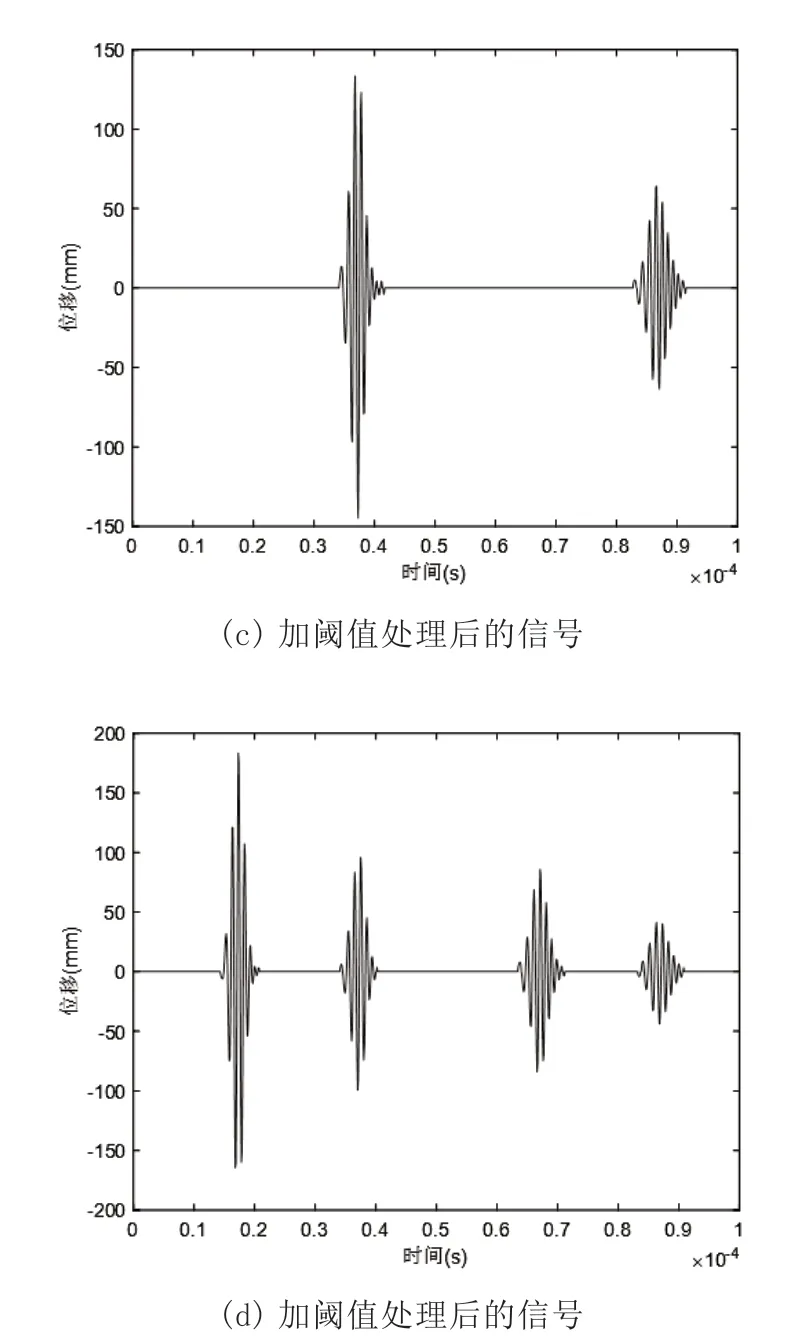
图3

图4 反映了激发出的S0模态的lamb 波在经过板内部的对称缺陷时lamb 波的变化。

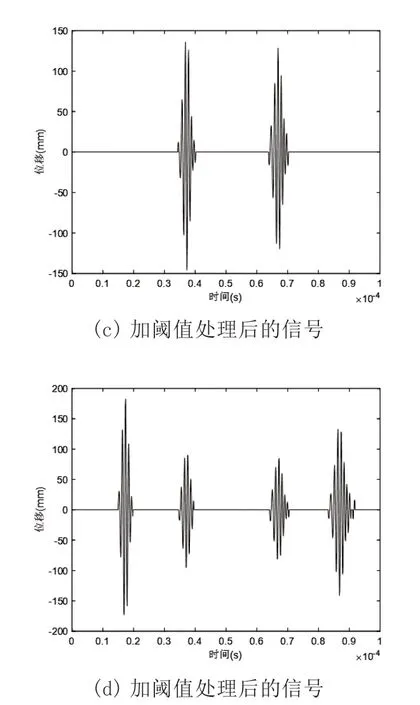
图4

2.2.2 单一模态lamb 波通过非对称缺陷

图5 反映了激发出的A0模态的lamb 波在经过板外部的一般缺陷时lamb 波的变化。图5(c)有两个波包，从左至右依次是缺陷透射S0模态的lamb 波和缺陷透射A0模态的lamb波；图5(d)从左至右依次为从边界激发出的还未经过缺陷的A0模态lamb 波、缺陷反射S0模态的lamb 波和缺陷反射A0模态的lamb 波。

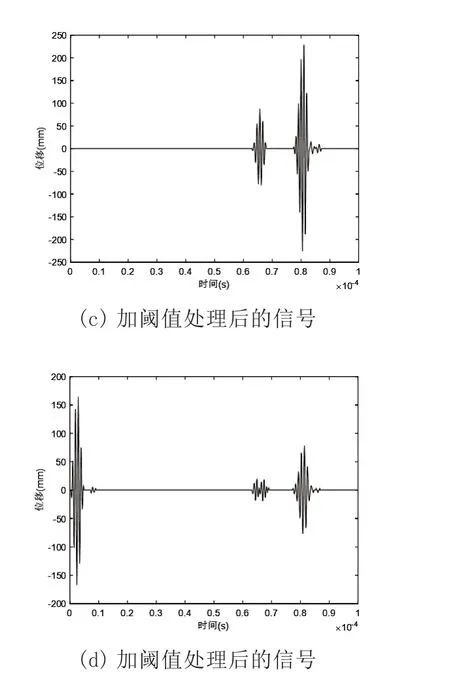
图5

图6 反映了激发出的S0模态的lamb 波在经过板外部的一般缺陷时lamb 波的变化。图6(c)中一共有四列波，从左至右依次为缺陷透射S0模态的lamb 波、缺陷透射A0模态的lamb 波、右边界反射S0模态的lamb 波和右边界反射A0模态的lamb 波；图6(d)中一共有六个波包，从左至右依次为从边界激发出的还未经过缺陷的S0模态lamb 波、缺陷反射S0模态的lamb 波、缺陷反射A0模态的lamb 波、左边界反射S0模态的lamb 波、左边界反射A0模态的lamb 波和第二次缺陷透射波及反射波叠加的S0模态的lamb 波。

图6

3 结语

3.1 单一模态lamb 波受对称缺陷的影响

（1）S 或A 类型的lamb 波在通过对称缺陷时存在反射和透射现象。

（2）单一模态lamb 波在被对称缺陷反射时的幅值会明显下降，透射过去的lamb 波幅值仅出现少许变化。

3.2 单一模态lamb 波受非对称缺陷的影响

（1）S 或A 类型的lamb 波在通过非对称缺陷时存在反射和透射现象。

（2）单一模态lamb 波在被非对称缺陷反射时的幅值会明显下降，透射过去的lamb 波幅值仅出现少许变化。注：图4(a)的第二个波包幅值没有明显下降的原因是结构对称，两列波在同一时间到达缺陷处，缺陷反射和透射的lamb 波刚好叠加。

（3）单一模态lamb 波在通过板中非对称缺陷时会发生模态转换既有新的类型的lamb 波出现。

（4）单一模态lamb 波在通过板中非对称缺陷时产生的新的模态的lamb 波的幅值要远小于初始被激励出的模态的lamb 波。