位移模式对复合砂卵石地层土压力的影响分析

朱 闪

(中铁十八局集团有限公司,天津 300000)

0 引言

在基础结构的设计中，挡土墙后土压力的探索是一个重要的研究课题，被广泛应用于道路、边坡、高层建筑和地铁修建等领域。滑裂面形状的合理性影响着土压力理论计算方法的准确性，其中最常用的滑裂面假定为平面形和对数螺旋形[1]。为确定滑裂面与位移模式的关系，李秀梅等[2]通过离散单元法，分析了挡土墙背离土体平移T模式及绕墙底转动RB 2种位移模式下的砂土土压力分布及滑裂面形状的不同；陈国舟等[3]采用离散元软件建立了圆形挡土墙结构，分析了桶形挡土墙上的土压力与墙体位移大小有关；胡靖等[4]采用离散元法对不同初始孔隙比的粒状土进行压缩试验模拟，分析了初始应力状态、初始孔隙比和应力历史对静止土压力系数的影响；陈奕柏等[5]应用水平层分析法和改进的库仑公式，推导出考虑挡墙变位影响的非极限土压力合力及其作用点位置、土压力分布计算式；孟庆宇[6]采用有限差分与模型试验的方法研究了砂性土的锚拉式悬臂式挡土墙土压力随位移的变化关系。以上研究基于经典土压力理论，针对不同挡土墙位移和变形模式、不同的初始条件等情况对土压力计算方法进行了修正和完善。但目前的研究主要停留在对单一性质土体的破坏模式及土压力变化规律的研究上，尚未有研究揭示上覆黏土的卵石地层在主动模式下的破坏极限问题、土压力与土体类型和位移模式的联系以及滑裂面的形成情况。

现基于离散元法(PFC2D)，结合洛阳卵石地层的工程特性，分析了不同位移模式下上覆黏土的卵石地层条件下土压力的主动极限状态、土压力的分布规律、土压力合力随位移的变化规律和滑裂面形状，并将上述结果与单一卵石地层情况作对比。此分析结果将弥补现行经典土压力计算方法中仅仅基于砂土平面型滑裂面假定的局限性。

1 离散元模型

在数值实验过程中，用作卵石和上覆黏土的颗粒材料必须满足一定的要求，其中包括：颗粒粒径分布、颗粒连接模型以及细观参数设置。为了较真实地模拟土体的实际物理力学特性，采用Itasca公司提供的Fishtank工具包[7]，采用直剪实验对细观颗粒的宏观参数进行标定。模型尺寸为宽×高=30 m×15 m的矩形区域，底部5 m为垫层，用于减少边界效应造成的应力集中现象。图 1为上覆黏土的模型图，卵石层厚10 m，黏性土层厚5 m，右侧自地面向下10 m深为运动墙体。图2为全卵石地层模型。通过编制fish函数，控制运动墙体以5×10-4/s的速率进行平动或转动[8]，固定时间步为4×10-4。试样参数如下：卵石采用粒径分布为0.04～0.12 m的圆球(ball)组成，颗粒间连接模型采用线性接触刚度模型；黏性土粒径分布范围为0.03～0.06 m，颗粒连接类型为linear contact bond。综合考虑实际的颗粒参数和数值实验要求，数值实验的颗粒具体参数取值见表1。

图1 上覆黏土地层模型(单位：m)

图2 全卵石地层模型

表1 参数取值

在生成模型之前，先对上述颗粒材料进行双轴剪切实验，得到卵石摩擦角约为36°，黏性土黏聚力12 kPa，摩擦角约24°，黏性土颗粒初始处于bond状态。

通过在墙背侧设置半径0.25 m的监测圆盘(measure)[3]，用于记录墙背侧土体内侧的土压力分布。在墙体发生运动的过程中让测量圆随着墙体同步发生运动并始终保持和墙体相切的状态。

2 分析结果

2.1 土体主动极限状态

土体的主动极限位移是衡量挡土墙后土体在主动位移模式下变形到破坏的一个重要分界值。在刚性墙发生主动位移过程中，可以根据速度场的变化规律分析土体状态的变化，并确定土体达到主动极限状态时的位移。图3(a)～图3(f)给出了全卵石土挡土墙背离土体发生平移时的速度场变化情况。从图中可以看出，挡土墙平移10～20 mm(见图3(b)～图3(c))时，背侧土体形成槽型的大速度区。随着位移进一步发展(见图3(c)～图3(d))，滑裂面逐渐左移，并从曲面发展成稳定的平面。当位移量超过30 mm时(见图3(d)～图3(f))，滑移面基本稳定，由此确定土体达到主动极限状态。卵石的主动极限位移为(0.3%～0.4%)H(H为挡土墙高度)。

图3 卵石地层速度场

上覆黏土时，为确定复合地层条件下的主动极限位移，图4(a)～图4(f)分别给出了卵石上覆黏土的地层条件下，土体随挡墙平移时的速度场变化情况。与全卵石土相比，存在以下异同点。当挡土墙位移较小时(见图4(b)～图4(c))，背侧土体出现槽型的滑裂面，与全卵石情况类似。当位移发展到30 mm时(见图4(d))，下层卵石土滑裂面发展成平面并基本稳定，但上覆黏土由于具有一定的黏聚力，而尚未达到其主动位移极限状态，此时滑裂面呈现出鼓出状。当位移量继续增加到60 mm时(见图4(f))，黏性土破坏范围逐渐增大，滑裂面左移并从曲面发展为平面。从滑裂面的形成可以看出，卵石上覆黏性土时，卵石和黏性土的主动极限位移状态应分别考虑。其中。卵石土可取0.3%H，所述黏性土可取(0.4%～0.6%)H。

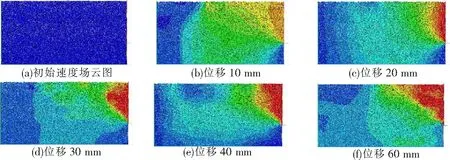
图4 卵石上覆黏性土速度场

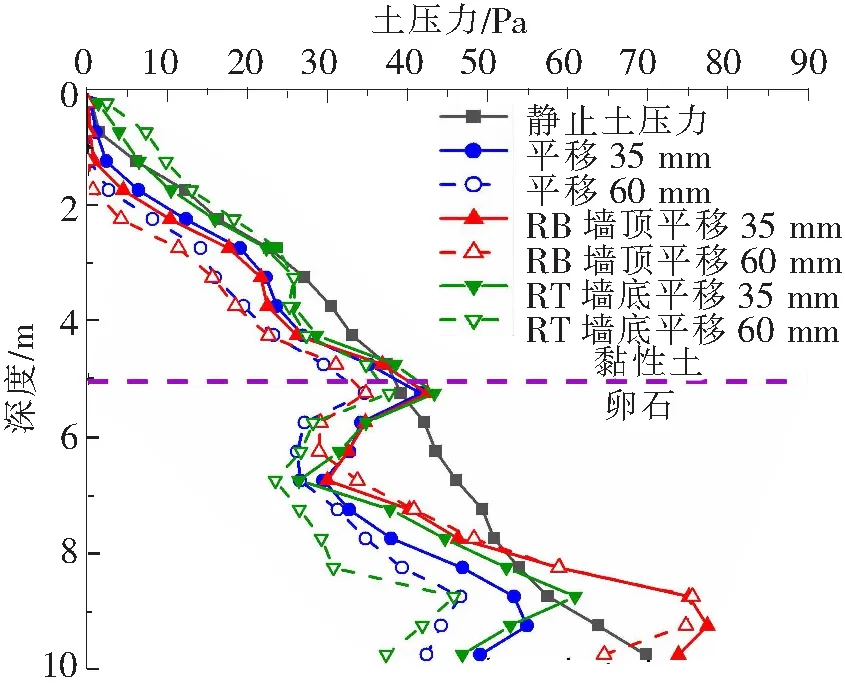
图5 不同模式下墙后土压力分布

2.2 土压力分布规律

根据挡土墙达到主动极限状态的不同，常见的墙体位移形态可以划分为3种基本模式：平移模式(T)、绕墙底转动(RB)和绕墙顶转动(RT)，它们分别对应着挡土墙不同的破坏状态。为区分位移模式和上覆黏土对土压力分布的影响，图5给出了卵石上覆黏土主动情况在不同变形模式下的土压力分布。其中，当位移达到35 mm时，卵石土达到主动极限平衡状态；当位移达到60 mm时，黏性土均达到极限位移状态。

从图5可知，静止土压力几乎随着深度增加逐渐增大。在T模式下，当挡土墙背离土侧运动超过35 mm时，卵石土达到主动极限状态，在土体分界面处出现了明显的不连续现象。合理的解释是，由于土层间剪应力[9]的作用，土压力随深度的过度形式为曲线型，而非朗肯理论描绘的折线突变型。曲线过渡深度范围为土层分界面以下1.5 m范围内。

当挡土墙位移分别达到卵石和黏性土主动极限状态时(0.3%H和0.6%H)，卵石和黏性土的土压力分布出现不同形态的变化[10]。T模式下，卵石和黏性土压力值均随位移增加呈现逐渐下降的趋势。RB模式下，上覆黏土的土压力随着位移增加而减小，幅度较T模式大，下层卵石土压力沿深度斜率更陡。RT模式下，上覆黏土的土压力分布与静止土压力相比变化不大，但下层卵石土压力减少幅度较大。

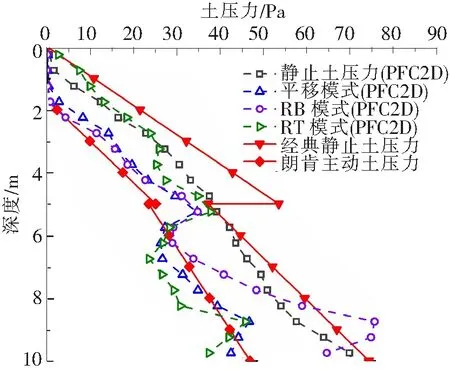
由于仅使用土压力分布很难直观地反映挡土墙背侧的受力状况，故通常采用土压力的合力来衡量。图6和图7对比了全卵石地层和上覆黏土地层条件下，土压力合力在不同位移模式下随位移的变化规律。土压力合力总体呈现先快后慢的减少趋势，依据减少斜率的快慢，可以分为几个不同的阶段，并且相邻阶段分界位移对应不同土体的极限位移。通过对比可以得出，全卵石地层土压力变化呈现为2阶段，而上覆黏土层时为3阶段。相同地层条件下，主动土压力合力满足T模式

图6 卵石层土压力合力变化关系

图7 上覆黏土土压力合力变化关系

全卵石的情况下，根据土压力减少速率的差异可以将位移过程分成2阶段：第一阶段，当位移较小时，土体尚未达到主动极限位移状态，此时土压力合力减少速率较快；当位移增大并接近一个临界值时，初始变形完全释放，然后合力下跌，进入第二个平缓减小的阶段。根据临界值进行判断可知，T、RB和RT模式下的主动极限位移取值不同，分别为0.35%H、0.45%H和0.5%H。

上覆黏土时，土压力合力变化可以分为3个阶段，出现了2个临界点。在第一阶段，土压力合力减少速率较快，该阶段卵石土和黏土的应力处于释放阶段，直到位移达到卵石土的主动极限位移值。随后进入第二发展阶段，该阶段土压力合力减少速率比第一阶段小，直到黏土达到极限状态，黏性土的滑裂面形成，土压力合力第二次下跌。最后进入第三个缓慢减少的阶段，表明整个土体已发生破坏。根据临界位移判断，此时卵石土的主动极限位移在T、RB和RT模式下的取值分别为0.25%H、0.35%H和0.20%H，比全卵石的极限位移值略低，而黏性土的主动极限位移值则分别达到了0.65%H、0.8%H和0.9%H。

2.3 土体滑裂面

土体滑裂面形状表明土体达到塑性极限时土体破坏能够发生的范围，也被用作极限平衡或者极限分析的基本假设和前提。例如，库伦土压力和朗肯土压力的平面型滑裂面，Michalowski[11]提出的对数螺旋滑裂面。为了得到位移模式对滑裂面的影响，图8～图10对比了T、RB和RT这3种位移模式下达到主动极限位移时的速度场。

图8 T模式速度场

图9 RB模式速度场

图10 RT模式速度场

由图 8可知，T模式下，全卵石的滑裂区为平面楔形块，滑裂面从挡土墙底部向上发展，楔形块顶宽较大。上覆黏土时，由于受到黏聚力的影响[12]，仅出现部分破坏，所以整体破坏模式呈现为中部鼓出状，滑裂面顶宽较小。

比较图 9、图 10可知，RB模式下，土体滑动区域集中于地表浅层一定区域，滑裂面不经过墙底，全卵石的滑裂区仍为平面楔形体；上覆黏土时，其滑裂面为对数螺旋的曲面型，顶宽比全卵石的情况窄。RT模式下，2种地层条件下的滑裂面相近，均为不贯穿到地面的耳形破坏区域。

3 验证与对比

3.1 主动极限位移

表2列出了本文结果与文献结果的对比[11-14]，主动极限位移与土体类别和位移模式有关。在相同的模式条件下，砂性土的主动极限位移通常略小于黏性土。对比不同位移模式可知，主动极限位移仍大体满足T模式≤RT模式≤RB模式。

表2 主动极限位移对比

3.2 与经典土压力理论对比

为说明土压力随位移变化存在的渐变性规律，将实验结果与经典土压力计算方法作对比。根据位移状态不同，土压力分为静止土压力、主动土压力和被动土压力，其中后两者分别对应主动和被动平移模式下的极限土压力。

静止土压力计算公式为

p0=(1-sinφ′)σv′

(1)

图11 土压力分布与经典理论的对比

主动土压力采用朗肯公式为

pa=σv′tan2(45°-φ/2)-2ctan(45°-φ/2)

(2)

式中，σv′为竖向有效应力，浅埋条件下取为上覆土重力。

为了验证离散元数值解的合理性，图11比较了本文离散元结果和经典理论下土压力分布的差别。由图11可知，尽管土压力分布和经典理论有一定的区别，但土压力数值结果大致符合经典土压力的大小。主动土压力小于静止土压力，挡土墙发生主动位移时，土压力呈现渐变的趋势。对比不同位移模式的影响可知，朗肯土压力分布更接近于平移模式下的结果。不同位移模式对应的主动土压力分布大体在经典理论所述的静止土压力和主动土压力组成的范围。黏土层变化范围小于卵石土，卵石受位移作用土压力变化离散性更强。

4 结论

采用离散元软件PFC2D模拟上覆黏土卵石基坑挡土墙在不同位移模式下的土压力问题，得到以下结论：

(1)主动极限位移与土体类型和位移模式有关。全卵石土在平移模式下的主动极限位移为(0.3%～0.4%)H，小于RT和RB模式下的极限位移，黏土的主动极限位移高于卵石。

(2)主动土压力合力随主动位移呈阶梯状减小，变化阶段与土体的失稳先后顺序有关。卵石层优先于黏土发生破坏，且土压力在平移模式下下降最快。土压力分布形态变化不仅与土体类型有关，也受到位移模式的影响。

(3)滑裂面形状受上覆黏土的影响，平移模式和RB模式下的滑裂面形状均为曲面型，不同于全卵石的平面型，滑裂面顶宽和范围均小于全卵石的情况。RT模式下2种地层条件的滑裂面均为耳形。