深海钻井船大开口阶梯形月池水体的非线性共振特性研究

石 城，吕海宁，杨建民

（1.上海交通大学海洋工程国家重点实验室，上海200240;2.高新船舶与深海开发装备协同创新中心，上海200240）

0 引 言

钻井船对于海洋资源开发和海洋油气开采有着重要作用。钻井船的钻井模块为其开采的核心模块，位于船中部，水下设备和钻井设备通过船中部月池下放至水中。月池结构通常贯穿船体的甲板至船底，月池内的水体与外界水体连通，在外界波浪达到一定条件时，可能与月池内部水体产生共振现象。月池是钻井船的核心结构之一，理想的设计可以在一定程度下屏蔽恶劣的外部环境。也有可能在某些条件下月池内部水体与外部波浪发生共振，损害船体结构、月池内部设备以及船上人员安全。

月池内部的水体运动主要为船长方向的晃荡(sloshing)运动，以及垂向的升沉(heaving)运动。在实际情况中，两种运动同时存在互相叠加，同时船身的运动、月池内部水体的运动以及环境波浪互相耦合。在阶梯形的月池壁以及月池台阶处都有强烈的非线性特征，月池内部水体的多模态晃荡使得月池水体水动力问题十分复杂。这些问题受到国内外学者的广泛关注，许多问题仍有待解决。

可以看出，多数研究并没有关注船体不同自由度对月池内部水体爬升的影响。本文采用数值模拟与模型试验相结合的方法，研究了船体不同自由度对月池内水体爬升的影响，以及改变环境波高时，月池内部水体爬升幅值的响应情况。

1 数值计算

1.1 计算理论

对于非理想流体，其流场的控制方程包括连续性方程和动量方程，分别为

式中：t 为时间；ρ 为流体密度；u→为流体速度；G→为单位质量体积力，通常为重力加速度g；[ ]τ 为粘性应力张量。

本文数值模拟均为规则波，基于线性波浪理论中的Airy波理论和理想流体假设，二维速度势为

流体速度由以下两部分分量组成：

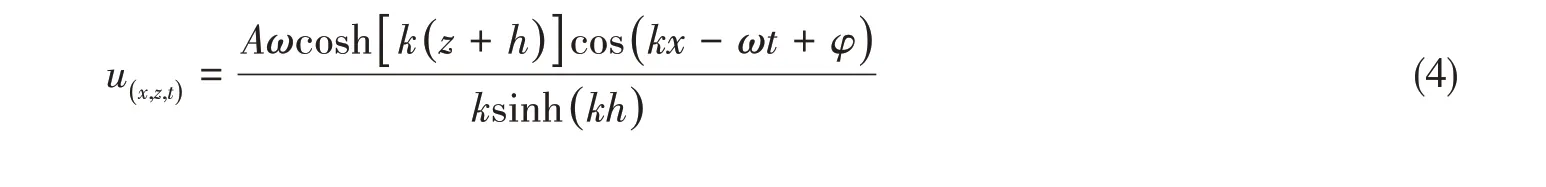
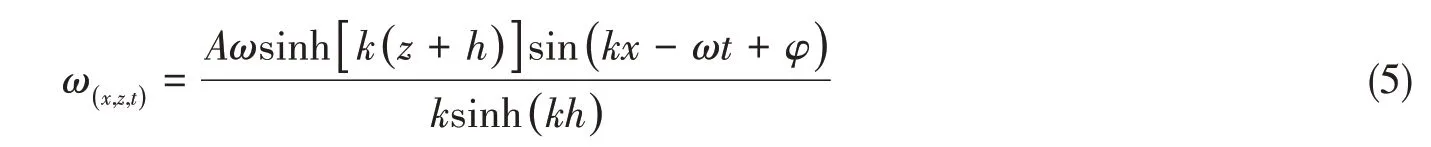
规则波的湍流模型采用SST k-w湍流模型，表达式为

式中，F1为混合函数，其计算公式为

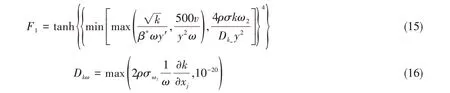
本文所使用的自由液面模拟方法为VOF 法，基本原理为定义一个流体域体积函数F 来追踪自由液面的变化，函数F 表示网格单元内流体体积占该单元总体体积的比值。若F=0，表明这是一个空单元，内部无流体；若F=1，表明该单元全部被流体所充满；F在0到1之间，表明该单元部分被流体充满，或者这种单元含有自由边界。除了F值介于0到1之间，还需要相邻单元中至少有一个是F=0的空单元。F的控制微分方程为

自由液面的法线方向可由F 的梯度来决定，得出各单元的F 值及其梯度之后，就可确定自由液面的位置和形状。

船体运动只考虑刚体运动。运动学上，刚体的任何运动都可以分解为一个平动加一个转动，刚体上任何一点的速度都可以表示为一个选定基点的速度加上这一点关于这个基点的转动速度，通常选择刚体的重心作为基点，刚体运动可表示为

1.2 数值水池建立与网格划分

数值模拟中，模型缩尺比为1∶50，在外部软件Rhino 中建立（如图1 所示）。选择计算流体力学Star-ccm+软件建立数值水池并进行数值计算。数值水池尾端设有消波区，水池入口端距船尾两倍船长，水池出口端距船尾三倍船长（如图2所示）。求解器采用隐式求解器，隐式求解器可以加强流体与船体运动之间耦合运动的计算，保证计算准确性。

图1 带月池钻井船模型Fig.1 Drilling vessel model

图2 数值水池及网格划分Fig.2 Numerical wave tank and meshing model

本文采用重叠网格进行数值模拟，网格总量为640万个。对自由液面垂向及纵向均进行网格细化，数值模拟保证在每个波高内有超过25 个网格，在每个波长内有超过160 个网格。计算时间步长Δt=0.04 s，船体网格划分及距数值水池入口处1 m 的波形如图3所示，波浪在数值水池内可以保证无衰传播。经过验证确定，目前的计算精度与计算速度可以得到较好的兼顾。

在数值模拟中，船体自由度分成三种不同情况。Case 1：船体静止；Case 2：船体有垂荡运动；Case 3：船体有垂荡及纵摇运动。本文还对比三种环境波高作用时，月池内部水体爬升情况。具体工况如表1所示。

表1 数值模拟工况Tab.1 Numerical circumstances

2 模型试验

本试验的模型缩尺比为λ=1∶50，模型按照缩尺比进行制作。在模型试验中，首先采用不同频率环境波浪进行试验，并根据月池内部水体响应情况确定船体共振频率。后续试验采用的环境波浪频率均为此共振频率，监测月池内部自由液面升高情况。本试验在上海交通大学海洋深水试验池进行。

2.1 钻井船模型

本次试验研究的钻井船船长约为180 m，船中有矩形大开口带阶梯月池，模型试验情况如图4 所示。为了防止模型在波浪作用下产生横荡或纵荡等位移，试验过程对钻井船进行水平系泊。试验内容包括静水衰减试验、白噪声试验和规则波试验。模型试验中的钻井船模型与实船参数及模型试验照片如表2和图4所示。

表2 船体及月池参数Tab.2 Geometric parameters of ship and moonpool

图4 钻井船模型试验Fig.4 Model experiment

在模型试验中对月池内部A、C、F 三处进行波浪爬升监测。坐标原点取在船尾处，各个监测点的坐标和位置如表3及图5所示（A与F并非月池最前端和最后端），模型试验系泊情况如图6所示。

表3 各监测点坐标值Tab.3 Coordinates of monitoring points

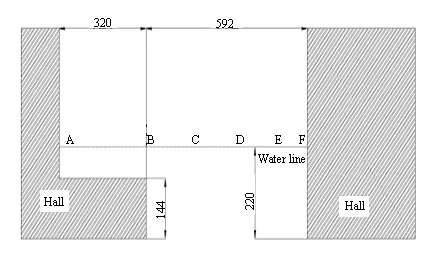
图5 月池内部监测点位置示意图Fig.5 Monitoring points

图6 模型试验水平系泊示意图Fig.6 Horizontal mooring method

2.2 波浪频率选定

本次模型试验首先采用不同频率的环境波浪进行模型试验，通过观测月池前后端的监测点C 处及F 处的自由液体面爬升情况，不同频率下监测点波浪爬升情况如图7 所示，最终得出模型试验的共振频率f'=0.92 Hz。考虑到模型试验中船体仍然存在除纵摇和垂荡外的其他自由度的微幅运动（数值计算中不存在），故本文基于船体最多仅有垂荡和纵摇两个自由度的情况，进行数值模拟，计算得到共振频率f=0.87 Hz，f 与f'相差甚小，对月池内水体爬升影响甚微。本文数值计算中的环境波浪频率均取此共振频率。

图7 不同波浪频率下的水体波高Fig.7 Wave elevations under different wave frequencies

3 计算结果与分析

3.1 数值模拟与模型试验结果对比

对比月池两个端点A、F处模型试验及数值计算结果（见图8），模型试验情况下的内部水体爬升幅值略高于数值计算结果（如图8 所示）。尽管模型试验时对船体进行了水平系泊，船体其他自由度的运动仍然无法避免，结果存在微小偏差，说明数值模拟与模型试验结果吻合较好。

图8 A和F处数值结果与试验结果对比Fig.8 Numerical and experimental results at monitoring points of A and F

3.2 船体不同自由度运动对月池内部水体爬升的影响

3.2.1 船体垂荡运动对月池内部水体爬升的影响

为了探究船体垂荡运动对月池内部水体爬升产生的影响，分别对船体静止（static）以及船体仅具有垂荡自由度（heaving）时进行数值模拟。环境波高h=0.04 m，月池内各处水体爬升情况如图9所示。

由图9 可见，船体具有垂荡自由度时(Case 2)，月池内部的波浪爬升幅值远高于在船体静止时(Case 1)的爬升幅值。船体垂荡自由度可以对月池内部水体爬升幅值产生激励作用，在研究月池共振问题时，船体运动不可忽略。

3.2.2 船体纵摇运动对月池内部水体爬升的影响

为了探究船体纵摇运动对月池内部水体爬升的影响，对船体释放垂荡及纵摇自由度（Case 3）进行数值模拟，环境波高仍为h=0.04 m，与船体仅具有垂荡运动（Case 2）的模拟结果进行对比。结果如图10所示。

图10 Case2及Case3时各处水体爬升对比Fig.10 Wave elevations under Case2 and Case3

对比Case 2与Case 3月池内部A-E处的自由液面升高情况，可以发现，A处水体爬升幅值在Case 3时相对于Case 2 有大幅提升，其他监测点处自由液面爬升幅值也有小幅增加。船体纵摇运动会对月池内部水体晃荡幅值产生放大，由于浅水效应，A 处水体爬升幅值增幅较大。同一监测点在Case 2 与Case 3两种情况下月池内水体晃荡周期不同，船体纵摇运动会对月池内部水体晃荡周期产生影响。

3.3 波高对月池内部水体爬升的影响

本文探究环境波高对月池内部水体爬升的影响，增加环境波高至h=0.06m和0.08 m。月池内部各监测点水体爬升情况如图11和图12所示。

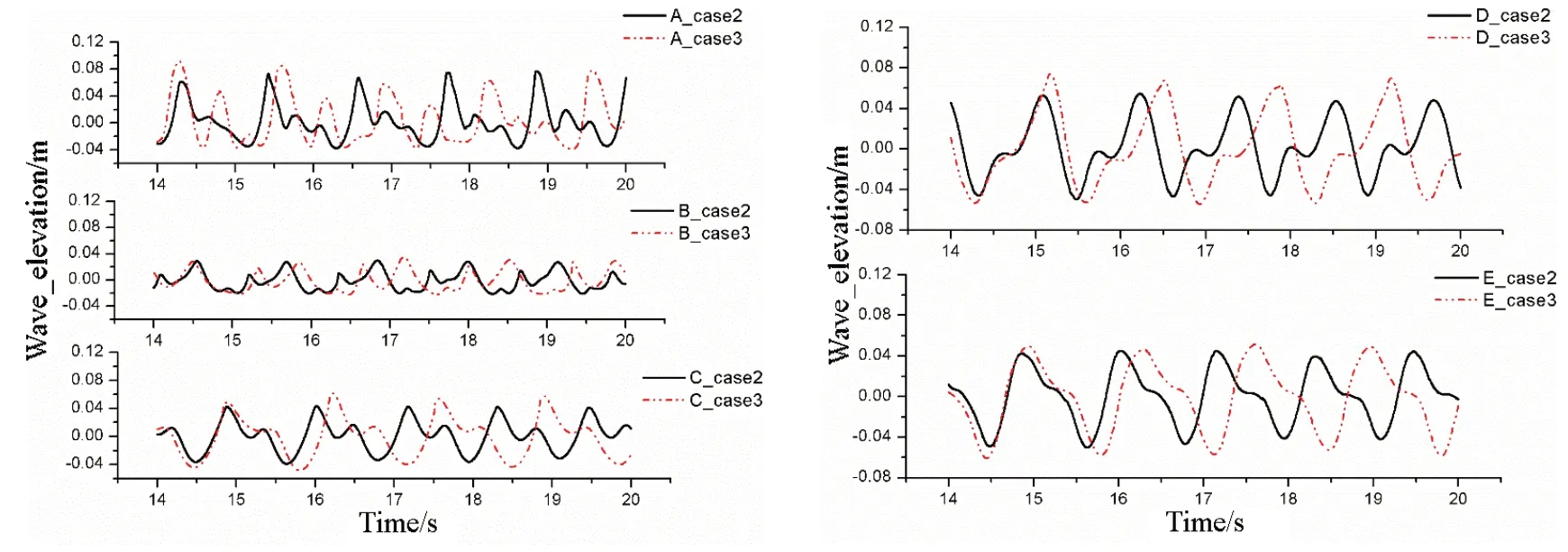
图11 波高h=0.06 m，Case 2及Case 3时各处水体爬升对比Fig.11 Wave elevations under Case 2 and Case 3 at a wave height of 0.06 m

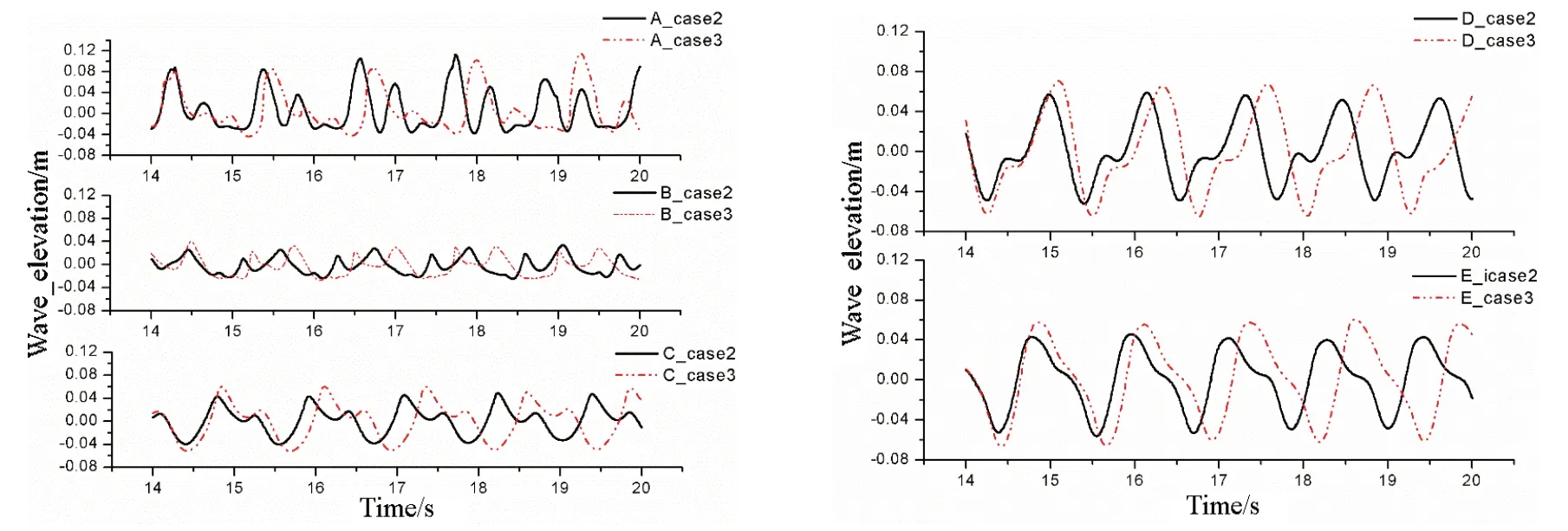
图12 波高h=0.08 m，Case 2及Case 3时各处水体爬升对比Fig.12 Wave elevations under Case 2 and Case 3 at a wave height of 0.08 m

分析A、B 处波浪爬升幅值，自由液面经历一次峰值后，随即又经历了一次幅值较低的二次爬升。这种二次爬升现象在A、B 处明显，且环境波高增加时二次爬升幅值增加。在Case 3 情况下波浪的二次爬升幅值明显高于Case 2 时的幅值。二次爬升现象源于月池内部水体的多模态晃荡，是强非线性的体现，且船体纵摇会增加各阶晃荡的幅值。

月池问题的强非线性使得月池内部水体多模态晃荡问题较为复杂。为探究月池内部水体晃荡各模态对应的频率及幅值情况，本文对波高h=0.08 m，船体具有垂荡及纵摇运动时（Case 3）的数值结果进行频域分析，结果如图13所示。

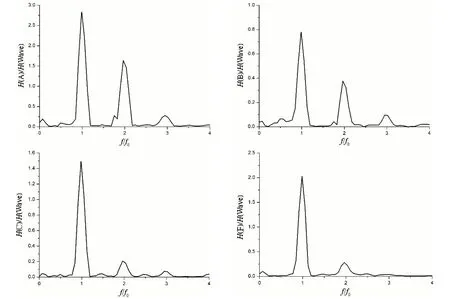
图13 A、B、C、F处频域分析Fig.13 Analysis of frequency domains at monitoring points of A,B,C and F

经过四点处的频域分析可以发现，各处均存在不同幅值的晃荡模态。主共振频率为f0=0.87 Hz，与试验测量值吻合，波浪频率为2f0及3f0时，月池内部产生高阶爬升现象。A 处的水体主模态爬升幅值以及其他模态爬升幅值均高于其他位置，B 处水体的各阶模态爬升幅值均小于波幅，这是由月池的后端（A处）浅水效应及月池边界的强非线性所引起的。

统计A-E 各监测点在环境波高不同、船体运动自由度不同情况下波浪爬升高幅值，结果如图14所示。

由图14 可知，当环境波高由h=0.04 m 上升至h=0.06 m 时，A 处自由液面爬升幅值由0.045 m 增加至0.09 m，达到了之前的约2 倍；波高继续增加至0.08 m时，A 处波浪爬升幅值达到0.12 m。环境波高由0.04 m 上升至0.06 m 时，C、D、E 处的自由液面爬升幅值均有小幅增加；波高达到0.08 m 时，C、D、E 处波浪幅值变化很小。月池内水体运动有强烈的非线性，这使得在环境波高线性增加时，内部水体响应并非线性，而是幅值增量趋缓。

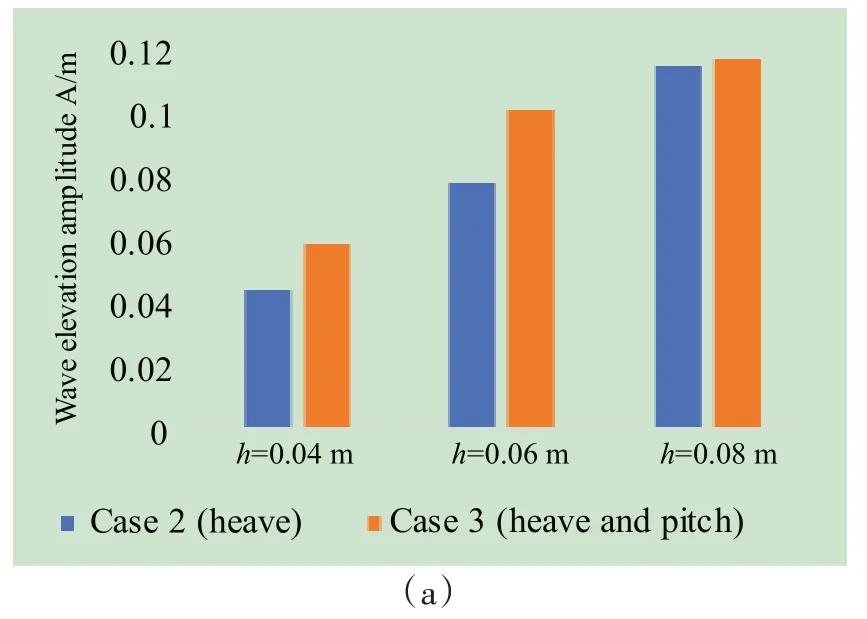
图14 不同船体自由度、不同波高时，月池内A-E处自由液面幅值统计Fig.14 Statistics of wave elevations under different ship motions and different outside wave heights

4 结 论

本文通过改变船体运动自由度以及环境波浪波高，对月池内部水体爬升进行了探究，并将对应数值结果与模型试验结果进行了对比，验证了数值模拟的准确性，得到了以下结论：

（1）月池会对外部水体产生屏蔽作用，月池内部水体滞后于外界波浪；

（2）船体垂荡、纵摇运动都会使月池内部水体爬升幅值增加，由于月池壁处的浅水效应，月池后端(A处)爬升幅值增量最大，研究月池共振问题时船体运动不可忽略；

（3）船体纵摇运动与环境波浪发生耦合，会影响月池内部水体的二次爬升幅值，也会影响内部水体晃荡周期；

（4）月池内部水体运动具有强非线性，水体存在多模态晃荡运动；

（5）由于月池内部水体的强非线性，环境波浪波高线性增加时，内部水体爬升幅值并非线性响应，而是幅值增量趋缓。