GNSS偏差及其研究进展

王含宇，宋淑丽，周伟莉，陈钦明

(1.中国科学院 上海天文台 天文地球动力学中心，上海200030；2.中国科学院大学，北京100049)

1 引 言

在全球卫星导航系统(global navigation satellite system,GNSS)的发展历程中，美国和俄罗斯的卫星导航系统不断地发展并进行现代化改善，其他国家和地区同时也争相建设自己的卫星系统并发展相关产业，不同卫星导航系统之间相互融合与借鉴，极大地推动了GNSS技术的进步。因此，GNSS的服务能力不断提升，达到了质的飞跃；与GNSS技术相关的应用领域不断扩大，已成为人们生活中不可缺少的一部分。在GNSS的应用日益广泛的背景下，研究者和用户越来越不满足于现在的成绩，追求更高质量的数据、更好的数据处理方法，以及获取更精密的产品为其主要目标之一。在导航定位相关方面的应用中，能够更好地改正、估算甚至完全消除GNSS信号传输过程中的各种误差，是获取高精度产品的先决条件。其中，GNSS设备引起的时间延迟(简称为设备时延)是主要误差源之一。

GNSS的设备时延(或称之为硬件延迟)是指GNSS信号在卫星和接收机传输过程中受到设备通道环境(如其中的数字滤波器)影响产生的时间延迟。其中，将信号从产生点到达卫星天线相位中心，经过设备通道的时间延迟称为卫星发射设备时延；从接收机天线相位中心到真正信号处理点的时间延迟称为接收机设备时间延迟。GNSS伪距和载波相位观测方程中，设备时延通常作为方程中的附加项，包括接收机和卫星相关的设备时延参数。而在实际应用中，卫星和接收机的设备时延与相应的钟差高度相关，相位设备时延也与模糊度有关，不能完全分离，同时卫星与接收机的设备时延也无法完全区分开。因此，一般在数据处理过程中，设备时延作为相对偏差进行解算。表1列出目前常采用的处理与设备时延有关偏差的4种方法[1]。

表1 设备时延相关偏差的处理方法

在不同的应用中，需要考虑的设备时延略有差异，根据实际需要，对设备时延有关的偏差进行分类研究。在单个GNSS系统中，涉及到两个及以上信号的伪距处理时，由于不同信号/频率在通道中的传输时间不一样，需要考虑信号间相对伪距设备时延，即码间偏差(differential code bias,DCB)。当进行模糊度解算时，为了固定整周模糊度，出现了关于未校准的相位时延(uncalibrated phase delays,UPD)的研究。当使用多个频率的载波信号时，不同频率组合下的卫星钟差存在一定差异，需要考虑频间钟差偏差(inter-frequency clock bias,IFCB)。在进行多个系统联合处理时，就产生了系统偏差(inter-system bias,ISB)这一概念。

随着国际上对设备时延相关偏差的研究日益增多、应用趋于广泛，国际GNSS服务组织(The International GNSS Service,IGS)成立了偏差和校准工作组(The IGS Bias and Calibration Working Group,BCWG)，该工作组主要是对GNSS偏差领域进行相关的研究。它主要目的是探讨目前存在的设备时延定义与影响，给出适当、一致的处理规则，为用户提供相应的高质量产品。同时，关注不断出现的新GNSS系统和新信号，不断更新设备时延的定义、增加新内容，完善提供的产品服务。

本文将对与设备时延相关的GNSS偏差进行详细介绍。

2 码间偏差

由于测距码在传输或者接收过程中产生的设备时延不一致，在相同时刻不同频率间或者同频不同测距码间出现的设备时延偏差，即为DCB[2]。DCB是两个信号间的设备时延之差，值的大小受信号通道的影响，可达几纳秒甚至十几纳秒[3]。根据信号机制，可将DCB分为频内DCB和频间DCB，前者是指在同一个载波上因测距码不同造成的设备时延偏差，而后者指由于载波频率不同产生的设备时延偏差[3]。由于延迟产生的位置不同，又分为接收机DCB和卫星DCB[3]。

DCB是反演电离层总电子含量(total electron content,TEC)的主要误差源[4]。早在1991年，Coco等人在对GPS系统的电离层延迟精度进行确定时，发现在L波段之间存在设备时延相关的偏差，并认为在确定电离层总电子量时必须将该偏差从GPS观测中去除[5]。在GNSS的精密单点定位、时间同步等方面的应用中，也需要考虑DCB[7]。所以当涉及到两个及以上信号的伪距观测的处理时，需要考虑到DCB[8]。此外，由于接收机DCB与接收机的设备性能密切相关，对接收机DCB数值进行长期分析有利于研究接收机的变化[7]。随着高精度GNSS的广泛应用，DCB的作用不可或缺，DCB的研究也趋于完善。关于DCB的处理，频内DCB和频间DCB有所区别。

关于频内DCB的处理，可通过伪距观测值直接做差解算[9]。因为两个码信号调制在相同的载波频率上，可以忽略电离层的影响，伪距观测方程见式(1)：

将两个码P1,P2的伪距观测值直接做差可得DCB[9]，如公式(2)：

其中，P表示伪距观测值，ρ表示为接收机和卫星间的几何距离，dtr,dts分别表示接收机和卫星钟差，dr,ds分别表示接收机、卫星的伪距硬件延迟，T为对流层延迟，I为电离层延迟，ϵP1,ϵP2为伪距噪声改正。由于伪距观测值形成的观测噪声较大，无法完全忽略。可将上式观测值在一天内取平均值，削弱噪声，得到综合DCB观测值。

频内DCB参数在一段时间内(如一个月)比较稳定，可将其看作一个常数[10]。欧洲定轨中心(Center for Orbit Determination in Europe,CODE)2010年开始用上述方法解算GPS和GLONASS系统DCB产品并提供给用户。图1为该中心2019年1月卫星频内DCB和接收机频内DCB的月均值，图2展示了2019年1月G02,G08卫星和ALRT,COCO测站的频内DCB的时间序列图。

频间DCB参数可采用事先标定和软件估算两种方式得到[6]。卫星和接收机在出厂前，通常会标定设备时延，用户可直接使用[6]。随着设备使用时间的增加，卫星和接收机老化导致硬件性能会发生变化，同时在外界环境等多种因素的影响下，实际值与标定值产生差异[6]。Coco等学者将预发射校准值与估计值进行比较，结果表明四对卫星中有两对显示出极好的一致性，而另外两对差异显著，认为需要谨慎对待事先标定值[5]。因此更多的研究者和用户利用GNSS的实测数据对频间DCB进行解算，并且这些解算的数据可对标定的频间DCB进行监测[7]。

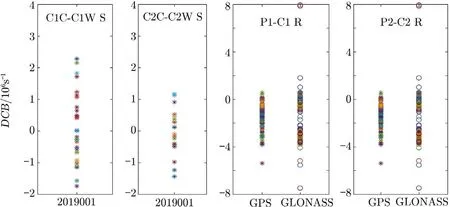
图1 2019年1月GPS/GLONASS的频内DCB[15]

图2 2019年1月G02,G08卫星和ALRT,COCO测站P1-C1 DCB的时间序列[15]

目前，关于频间DCB的估算方法有两种：(1)在电离层TEC建模时，将频间DCB参数与其他参数进行计算[3,11]；(2)采用经验或已有的电离层模型进行电离层延迟改正，然后再计算频间DCB参数[12]。方法二中解算的DCB值的质量很大程度上受到选取的电离层模型精度的影响[13]。但当选定模型后，可以对任意系统的DCB进行计算，并且可随时解算DCB，所以方法二较为方便快捷，极大地提高了DCB解算效率[14]。德国宇航中心采用了方法二，即利用全球电离层图(global ionospheric map,GIM)直接扣除电离层TEC，获得卫星和接收机的综合DCB，然后基于零均值基准约束方法分离卫星和接收机DCB参数[12]。采用该方法的不足之处是在电离层变化显著的地区(如赤道)，DCB的精度会随之下降[16]。而方法一的DCB是与电离层模型系数同时解算，结果会受到电离层解算精度的影响，所以需要选取分布均匀并且数量合理的GNSS测站[17]。

此外，目前在进行电离层建模时，假设接收机DCB日变化稳定，数据处理时一天计算一个参数[18]。对于采用码分多址技术的卫星系统来说，如GPS(global positioning system)、Galileo、北斗等，这样的处理方式是合理的。但是GLONASS(global navigation satellite system)卫星系统与前面三者不同，它采用的是频分多址技术来分离不同卫星传输信号[19]。在这种复用技术中，为不同卫星的载波分配了频带L1和L2内的相邻频率。不同的载波频率信号在接收通道中处理的方式不同，延迟也会因频率的不同有差异[19]；所以，将GLONASS系统中因载波频率不同而在传输或者接收通道中产生的设备时延的差值称之为频间偏差(inter-frequency bias,IFB)[20]。GLONASS卫星的IFB的值相差极大，处理方法上与频间DCB略有不同，需要将每个接收机通道中的IFB解算出来。目前IGS分析中心提供的DCB中不包含IFB。

3 未校准的相位时延

与伪距类似，载波信号的发射和接收也会受到各种偏差的影响[21]。在初始相位、卫星和接收机设备时延及其他因素的影响下，非差处理算出的载波相位模糊度包含了其他偏差，被模糊度吸收的这部分相位偏差表示为UPD[22]。由于整周模糊度计数不明确，UPD参数的整数部分与模糊度完全耦合，无法分离，一般只能测定不足载波信号一周的部分，将模糊度不为整周的小数部分称为小数周偏差(fractional cycle biases,FCB)[23]。一些学者有时会直接用UPD代替FCB进行表述。

精密单点定位(precise point positioning,PPP)作为非差数据处理中常见的定位方式，在相关应用中常常要考虑UPD。PPP主要是利用精密轨道和精密钟差等产品，在综合考虑各项误差改正的基础上，采用合理的参数估计方法(最小二乘法或卡尔曼滤波法等)，利用单台GNSS接收机实现绝对定位的技术[24]。由于PPP采用的是非差观测值，许多误差不能通过组成差分方程来减弱或者消除，因此各种误差源都必须加以考虑。载波相位模糊度的固定，可以提高PPP的精度和收敛速度[25]。PPP技术在获取大气延迟、动态精密定位、地壳运动及海洋潮位监测、精密授时、精准农业领域等方面均得到了很好的应用[25]。而更好、更快地固定模糊度是推动PPP发展的重要因素。

但是直接计算出来的模糊度不具有整数特性，是一个浮点解，即存在UPD，主要产生原因有三个[26]：(1)由于卫星和接收机产生的载波信号并非从零相位开始，并且初始相位未知，无法将其从模糊度中分离。(2)不同的信号在卫星端和接收机端传输中，由于信号的差异，会产生不同信号间设备时延，而该延迟会与模糊度耦合。(3)PPP使用的精密钟差产品主要是IGS或者是与IGS解算方式相近的精密产品，它们在计算钟差时一般使用无电离层组合形式并以伪距观测方程的钟差为基准；由于其精度不高，只有厘米级，在载波相位观测方程中，使用该钟差基准时，模糊度参数也会吸收部分钟差。

与模糊度浮点解的PPP相比，基于模糊度整数解的PPP优势主要有两个：提高定位的精度和缩短收敛时间。李星星等人[22]指出浮点解的PPP要达到厘米甚至毫米级精度，往往需要数小时以上的观测时间，并且其定位精度和可靠性不及双差固定解。近年来，国际上的研究重点转向PPP固定解，其关键是恢复非差模糊度的整数特性，因此提出了分离FCB的方法[24]。

越来越多的研究开始用计算FCB的方法进行模糊度固定，其中最常见的方法有星间单差估计法和整数钟法。星间单差估计法主要由Cabor[22]提出，之后Ge等人[27]根据他提出的方法做出部分改进：首先是利用多个(100左右)IGS地面观测网算出非差模糊度的浮点解，然后在卫星间做差消除接收机端的FCB；再利用MW组合估计宽巷模糊度，将其取整得到宽巷FCB改正数；再将宽巷模糊度带入无电离层组合中，固定窄巷模糊度，分离窄巷FCB改正数。而整数钟法则是计算非差宽巷的FCB改正数，利用宽巷FCB改正数来固定宽巷模糊度，然后估计包含了窄巷FCB的卫星钟差[28]。当获得FCB后，直接对无电离层组合下的宽巷和窄巷模糊度进行固定，得到PPP的模糊度整数解，获得高精度的结果，可更好地应用到实际中[29]。

目前武汉大学PRIDE(Positioning Racers to Image and Decipher the Earth)课题组提供了GPS C1W/C2W/L1C/L2C的卫星FCB，该数据是每颗星每个信号一天一个值[29]。图3为2020年1月1日所有GPS卫星4种信号的FCB值。由此可见，在同一天中，不同卫星、不同信号的FCB差异明显。图4表示为G01和G10两颗卫星在2020年1月份的时间序列图，可见在该时间段内同一卫星同一信号变化较稳定。法国CNES分析中心也提供了宽巷FCB，主要是利用整数钟法解算得到。

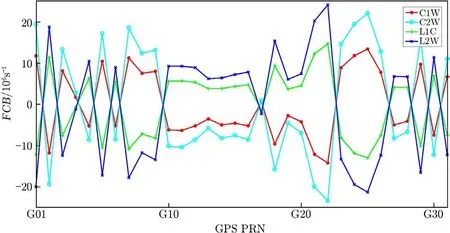
图3 2020年1月1日不同GPS卫星C1W/C2W/L1C/L2C的FCB[29]

与只有GPS-FCB方法相比，利用多个系统对不同系统的FCB值估计并进行应用，能够获得更快更好的定位结果。武汉大学测绘学院也在进行多GNSS系统FCB产品的研究，包括GPS,Galileo,BDS和QZSS等系统[30]。目前，关于FCB的研究虽然趋于成熟，但还在发展阶段，提供的产品也在逐步完善中。

图4 2020年1月G01,G10卫星C1W/C2W/L1C/L2C FCB的时间序列[29]

4 频间钟差偏差

美国的GPS、欧洲的Galileo、日本的QZSS(quasi-zenith satellite system)和中国的北斗均提供多频信号服务，多频信号的加入进一步推动了GNSS的发展。使用多频信号提高了定位精度和模糊度的解算速度。相比于双频信号，三频信号具有增加可观测的波长、降低噪声、减少电离层影响等优势[31]。利用三频信号可进行周跳探测和修复、模糊度固定等方面的应用，推动了高精度导航定位的发展。但受卫星、接收机硬件延迟、空间环境等影响，采用不同频率观测、观测组合解算的卫星钟差存在差异[32]。Montenbrucket等学者在研究GPS Block IIF卫星时，发现不同频率无电离层组合估计得到的钟差之间存在一定的差异，并将其定义为频间钟差偏差(inter-frequency clock bias,IFCB)，IFCB最大可以达到15 cm[33]。并且他们还认为IFCB的变化周期与卫星运行时相对于太阳高度角的变化相关联[33]。Li等学者在其基础上对PRN25和PRN01卫星的IFCB进行计算，并提出了解算频间相位偏差的方法，用于估算两个Block IIF卫星的IFCB，研究发现IFCB的变化对不同频率上无电离层组合的PPP收敛时间与定位精度均产生影响[34]。

在三频处理中，GNSS三频观测可以组合成两组无电离层组合的形式为[32]：

其中1,2,5代表频率，PIF,LIF分别表示无电离层组合下的伪距和载波相位观测值，ρ,dr,ds与公式(2)中相同，br,bs分别为接收机、卫星的相位硬件延迟，λ为无电离组合载波相位的波长，N为相位模糊度，ϵL为相位噪声改正。当采用两组无电离层组合进行卫星钟差解算时，参数化的卫星和接收机钟差会吸收对应的硬件偏差，所以会产生两组卫星、接收机钟差。将cdtr+dr1,2为频率1、2组合下解算的接收机钟差用δr1,2表示，cdts+ds1,2为频率1、2组合下解算的卫星钟差用δs1,2表示；cdtr+dr1,5为频率1、5组合下解算的接收机钟差用δr1,5表示，cdts+ds1,5为频率1、5组合下解算的卫星钟差用δs1,5表示。但同时解算两组接收机和卫星产品，不仅增加了时间成本也加剧了计算负担[35]。为了提高解算效率，提出了一种消除钟差产品不一致性的方法，即求解IFCB。主要思路是解算其中一个频率组合的钟差并将其作为基准，其他的钟差可用该基准加上IFCB表示[33]，即：

假设相位设备时延被模糊度吸收,将不同的频率组合(1/2和1/5)做差，其中接收机和卫星的几何距离以及对流层延迟会被消去，仅留下模糊度项和IFCB，而伪距的仅留下IFCB，具体如公式(5)所示：

初冬的天地干净、宽广、朴实，阳光则显得格外珍贵，照在玻璃窗上，让人不困思眠。趁这个残秋尽、冬未隆的日子里，不如与三五好友，围炉煮酒，在腾起的水汽中畅食畅饮，忘却拖沓了几个季度的疲惫。就算此时屋外寒风横虐，那也是时光恰好。

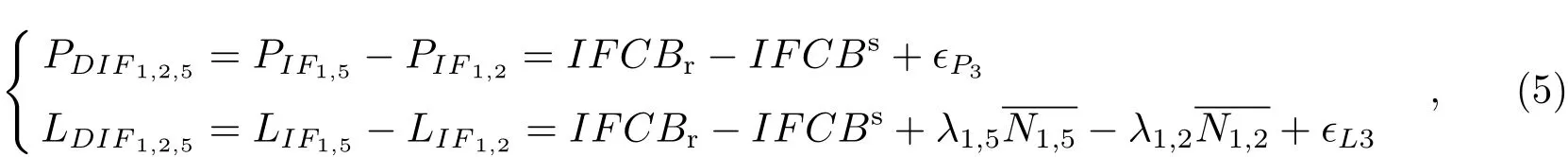
其中，δs表示IFCBs的变化部分，ifcbs为IFCBs的常数部分。卫星频间钟偏差的变化部分可通过相位观测方程进行解算。当历元间没有周跳发生时，将公式(5)的载波相位观测方程进行历元间作差，整周模糊度被消除，随之消除的还有常数IFCBr和IFCBs的常数部分。当利用单个测站，多个历元(如k个)进行计算时，每个历元的变化部分为：

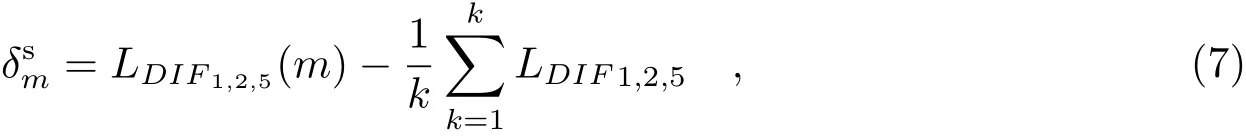
被模糊度吸收的部分可以通过伪距观测方程进行解算。但直接对历元进行求和取平均，得到的是卫星和接收机常数部分的和。为了得到ifcbs部分，消除接收机部分，可选择一个参考卫星进行相应的求解。

卫星IFCB的变化部分具有时变性，可建模为与太阳-卫星-地球角相关的周期函数；接收机IFCB可以看作一个常数[36]。所以IFCB可以提前被预估出来，应用于相关领域。

5 系统间偏差

系统间偏差是多个卫星导航系统进行联合导航、定位等应用时，必须要考虑的偏差[37–40]。因为不同的GNSS系统采用的坐标和时间基准不同，不同系统信号的结构、体制等有差异[38]，当不同GNSS信号在多模接收机通道中传输时，会产生接收机设备相关的时延偏差[39]。所以利用多系统GNSS数据进行融合解算时，需要考虑这些系统性的偏差[40]。一般认为ISB是一个卫星系统(如北斗)观测值与参考卫星系统(如GPS)的观测值放一起处理时，所需考虑的一个改正[23]。在实际应用中，由于系统间坐标基准的差异主要体现在卫星位置上，在多模GNSS数据处理时一般转换成相同的坐标系[40]，可以忽略坐标基准差对ISB的影响。所以，ISB主要包括了时间基准之差和接收机设备时延[41]。

随着多个GNSS系统的出现，很多学者对多模GNSS导航定位的方法进行了研究[41,42]，系统间偏差研究相应产生。解决ISB问题，可让多GNSS系统更好地联合应用，可用卫星数量剧增，从而增加了同一时刻同一地区观测到的卫星数[43]，卫星分布的几何结构得到了优化，降低了位置精度因子，有利于在环境恶劣地区(能够观测到的卫星数量较少的地区)进行导航定位[44]。

目前，国内外关于ISB的研究，主要包括ISB的处理方法研究，ISB的来源及特性研究，ISB建模预测研究等。无论在伪距还是在载波相位观测方程中，ISB均会存在[37]。但在不同的情况下，ISB的研究与定义略有差异。当多模GNSS联合网解时，整网内只估算一个基准钟差。但不同的信号频率和不同的卫星系统会产生不同的设备时延，而这些时延会被接收机钟差吸收，因此不同卫星系统的接收机钟差实际上存在差异[49]，所以需要在不同系统中引入一个偏差参数。例如在利用GPS(用G表示)和BDS(用C表示)进行联合处理时，一般选取GPS的接收机钟差作为两个系统的接收机钟差，用cdtr+drG表示，将引入的偏差参数用ISB表示，则两系统联合解算的无电离层组合观测方程为[49]：

ISB表示为系统C相对于系统G的系统间偏差。如果考虑不同卫星系统间时间基准的差异，ISB中还存在一个常数偏差参数[50]，用D表示，则ISB可表示为：

上述ISB公式表示的是采用码分多址技术的GNSS系统的系统间偏差。而如GLONASS卫星系统，采用频分多址技术来区分不同的卫星，它与其他GNSS系统间的ISB相比，还包括了不同卫星的频间偏差[51]。因此GLONASS的每颗卫星都要计算出1个ISB值，或者将每颗卫星的频间偏差去除。值得注意的是，当ISB参数与其他轨道产品联合解算时会产生秩亏，因此需要引入一个额外的约束条件[52]。目前有两种约束方法：一是选择一个特定的测站，令其ISB为零；二是令整个测站网的ISB和为零。目前，iGMAS上海天文台分析中心，采用上述第二种约束方法对BDS/GPS,Galileo/GPS,GLONASS/GPS的ISB进行解算。图5、图6、图7分别表示2018年9月17日到2019年9月19日10个相同测站的BDS,Galileo,GLONASS相对于GPS系统伪距ISB值的时间序列图。可见同一时间段内同一个测站下，Galileo/GPS和GLONASS/GPS之间ISB非常稳定，BDS/GPS的稳定性稍差。

图5 BDS/GPS ISB时间序列

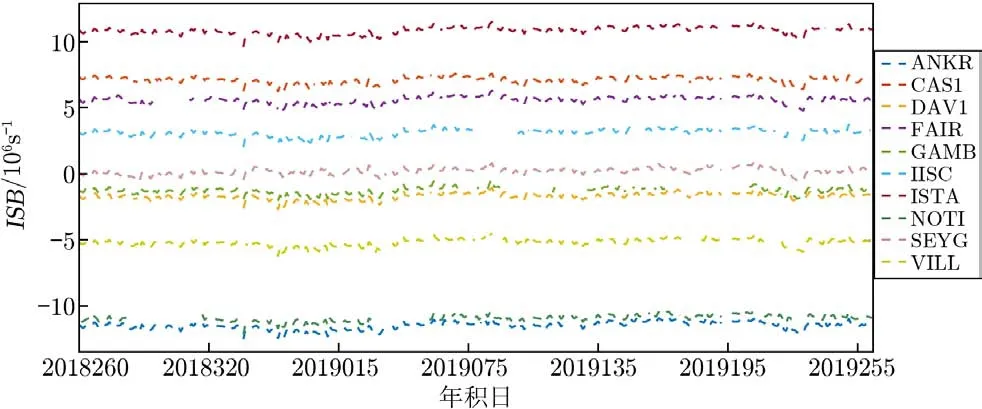
图6 Galileo/GPS ISB时间序列

有关多模GNSS定位的研究相对较多，主要包括相对定位与单点定位两种方式，ISB的处理策略也略有差异。

图7 GLONASS/GPS ISB时间序列

在相对定位中，时间基准偏差会在双差处理中消除，但是相对的接收机设备时延还会存在，所以仍然存在系统间偏差[53]。在相对定位中对ISB的处理又分为两种情况：(1)当系统间频率相同时，采用紧组合模型进行解算；使用该方法的模糊度还会保持整周特性[54]，但是需要两个系统间有相同频率的信号，相当于将两个系统看成单系统进行处理。(2)当系统间的频率不同时，采用松组合模型；该模型分别对不同的GNSS系统独立进行解算，系统间不进行交叉处理，使用该方法的伪距和相位ISB均可消除[55]。由于GPS和Galileo系统有频率相同的信号(L 1/E1,L5/E5a)，这两个系统常常采用紧组合的方式进行数据融合[56]。而在GPS/BDS联合处理中，较多采用松组合的相对定位模型[56,58]。在关于GPS/Galileo联合进行相对定位的ISB研究中，发现在接收机相同时ISB值差异很小，不需要考虑；而接收机不同时伪距ISB的相差很大，有的甚至达到几百纳秒[56]。

在单点定位中，ISB可作为一个附加参数进行计算，但是未知参数比较多，一般会引入一个约束条件[59]。不同的约束条件，获得的ISB不同。在静态单点定位中，一般使用精密星历及卫星钟差处理，这时ISB也不含时间基准差。当进行动态定位时，经常会采用广播星历进行数据处理，算出的ISB包含时间基准差[21]。对于精密单点定位来说，相位ISB与模糊度无法分离。在采用模糊度浮点解的情况下，相位ISB与模糊度会一起解算出来[60]。

虽然在不同应用中对ISB处理方式有差异，但很多研究均认为接收机类型和天线类型对ISB值有影响，在短期内ISB值稳定性较好[37,47]。因此，Jiang[62]、张辉[61]等人还对ISB进行建模，根据一周的ISB值预报一天的ISB值，并进行检验对比，证明预报结果较好，具有一定的可预报性。

目前，ISB主要还是作为多模GNSS数据处理的一个衍生产品，很少有学者对其进行专门的研究。当需要进行多系统联合处理时，一般根据自己对系统间偏差的理解进行处理，还未真正形成一个完全一致的概念。而且当采用不同的约束条件，也会解算出不同的ISB，限制了用户对ISB的使用。对于动态定位来说，如果能够将ISB进行预报，将极大地提高解算效率。但是现在对于ISB的研究较少，也极少有人对长期的ISB进行特性分析。ISB是多模GNSS联合应用必须考虑的一个偏差，如果能够更好地认识ISB，有利于多系统数据融合处理。

6 总结

本文主要介绍了四种在GNSS数据处理中与设备时延相关的偏差(码间偏差、未校准的设备时延、频间相位偏差及系统间偏差)的定义、计算方法和研究现状等。讨论了这些偏差的来源及其对GNSS应用的影响，并详细介绍了在实际应用中每个偏差的具体处理方法。

码间偏差可认为是两个信号伪距设备时延组合。当使用两个信号时，伪距观测量必然会受到与信号和频率相关的DCB的影响，因此在观测中需要考虑它。目前DCB发展最为完善，在许多应用中使用。未校准的相位时延主要是为了固定整周模糊度而提出的，一般研究的是其小数部分FCB，主要是由于相位设备时延与模糊度无法完全分离。为了更快更好地利用三频数据，以其中一个卫星钟差为参考，其他钟差再利用频间相位偏差与参考钟差进行转换。系统间偏差则是在多个系统组合应用时，由于不同GNSS系统基准、信号体制等差异产生的系统性偏差，是与设备时延有关的相对偏差。

随着多GNSS的迅速发展及应用需求的不断提高，GNSS相关偏差的研究越来越受到重视，这些与设备时延有关偏差的标定、监测和合理的处理方法，对提高GNSS的高精度服务性能至关重要。国际上相关的偏差还处在不断修订、完善的发展中。将这些设备时延相关的偏差进行系统的整合归纳，将它们具体地定义并对它们的异同进行区分与联系，将极大地便利今后在相关邻域的研究。