空间解析几何中一类多线共点问题的探讨

李明浩

【摘要】 本文利用向量法和坐标法给出了空间解析几何中一类多线共点问题的三种解法.一题多解可以培养学生的创新精神和发散性思维.

【关键词】空间解析几何;多线共点;向量法;坐标法

《空间解析几何》是数学专业本科生的一门重要的基础理论课程，主要研究空间线、面及其位置关系.多线共点问题是空间解析几何中一类常见的问题.本文利用向量法和坐标法给出了这类问题的几种解法，旨在培养学生从多角度分析问题和解决问题的能力，从而提升学生的创新精神和发散性思维.

下面我们以教材[1]中的一道多线共点问题为例，介绍这类问题的几种解法.

例1 证明四面体对棱中点的连线交于一点且互相平分.

证明一 设四面体ABCD的六条棱AB，CD，AD，BC，BD，AC的中点分别为E，F，H，G，I，J，如图1所示.连接EF并设EF的中点为O.连接IO，OJ，HO，OG，下面只需要证明IO=OJ，HO=OG即可.

对于上述例题，我们已知交点的位置，即位于对边中点连线的中点.我们如果交点的位置不明确，可以尝试利用向量法或坐标法先确定交点的位置.

例2 证明四面体对棱中点的连线交于一点.

解 设四面体ABCD及其各边中点如图1所示.连接HF和EG，显然有HF=12AC=EG，因此四边形HFGE为平行四边形，对角线EF和HG交于一点且互相平分.从而可得该交点的位置.然后再利用例1的三种解法进行求解就可以了.

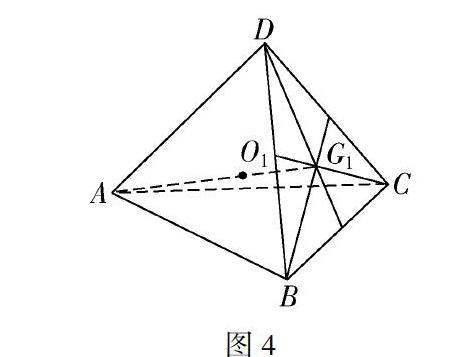
同理可得，如果O1与O3重合，则有λ1=λ3=3;如果O1与O4重合，则有λ1=λ4=3.因此λ1=λ2=λ3=λ4=3时，O1，O2，O3，O4重合，从而说明了四面体每一个顶点与对面重心所连的线段共点，并且该点到顶点的距离和到对面重心的距离之比为3∶1.

小 结

对于多线共点问题，如果已知交点的位置，则有如下两种思路：

（1）先在一条直线上选中该点，然后利用向量运算证明其他直线也经过该点.

（2）在每条直线上设出这些点，然后证明这些点重合.另外，思路（1）和（2）也可以用坐标来计算，有时坐标运算会更加简洁.

如果不知道交点的位置，可以采用向量法或坐标法确定该点的位置.

【参考文献】[1]吕林根，许子道.解析几何（第四版）[M].北京： 高等教育出版社，2006.

[2]吕林根.解析几何学习辅导书[M].北京： 高等教育出版社，2006.

[3]程炜.向量方法在空間解析几何教学中的应用[J].数学学习与研究，2015（5）：80，82.

[4]任琛琛，侯雨宏.共点线与共线点问题的探讨[J].南昌师范学院学报，2019（6）： 1-6.