应用GM(1,1)模型预测甘孜州接待国内游客人次

赵江林

【摘要】本文根据甘孜州2008～2018年接待国内游客人次建立GM（1，1）灰色预测模型.对原始序列进行对数变换，可使GM（1，1）预测模型精度较高.2019～2021年甘孜州接待国内游客人次呈上升趋势且增幅较大.则GM（1，1）模型可用于甘孜州接待国内游客人次的短中期预测.预测结果对甘孜州旅游发展具有一定的参考意义.

【关键词】接待国内游客人次;GM（1，1）模型;预测;甘孜州

1 引言

甘孜藏族自治州（简称甘孜州）旅游自然资源丰富，每年吸引大量国内游客前往，特别是自2017年雅康高速开通以后，进藏的时间大大缩短了，游客大量增加.甘孜州以瑰丽的高原地理地貌和独特的藏民族文化和生活令无数游客向往.因此，预测甘孜州旅游游客数量能够为旅游行业从业者和旅游政策制定者提供参考，提升甘孜旅游品牌形象，助推少数民族地区发展.

灰色预测模型基于数据本身，能够减少时间序列的随机性，具有所需样本量小、计算简便、预测效果较好等优点. GM（1，1）模型是灰色预测模型中最广泛使用的模型.当前GM（1，1）模型已被广泛应用在传染病、经济、农业、工程、体育等方面的预测.本文根据甘孜州2008～2018年接待国内游客人次建立GM（1，1）灰色预测模型，对甘孜州2019～2021年接待国内游客人次进行预测，为甘孜州旅游业的进一步发展提供参考.

2 资料与方法

2.1 资料

2008年至2018年四川省甘孜藏族自治州接待国内游客人次数据来源于甘孜州的历年国民经济和社会发展统计公报.

2.2 方法

2.2.1 GM（1，1）模型的建立

GM（1，1）模型是通过将离散随机的原始时间序列累加生成为随机性被显著削弱且较有规律的序列，建立相应的微分方程动态模型，然后利用该微分方程进行预测.下面我们建立灰色预测GM（1，1）模型.

2.2.2 模型检验

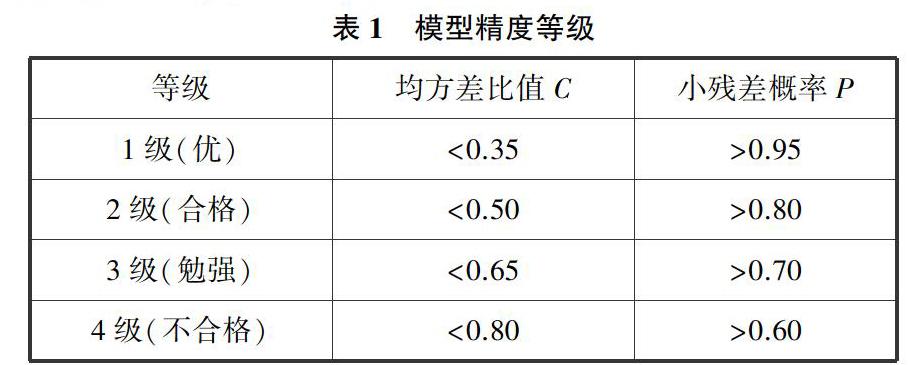
设原始序列为x（0），GM（1，1）模型的预测序列为x^（0），则x（0）的均值为x-=1n∑nk=1x（0）（k），x（0）的方差为s2x=1n-1∑nk=1x（0）（k）-x-2.设原始序列与预测序列的残差为ε，则残差的均值为ε-=1n∑nk=1ε（k），残差的方差为s2ε=1n-1∑nk=1ε（k）-ε-2.因此残差与原始序列的均方差比值为C=sεsx，小残差概率为P=Pε（k）-ε-<0.6745sx.若对于给定的均方差比值C0>0，当C0，当P>P0时，称模型为小残差概率合格模型.一般情况下，模型的模拟精度分为4级，如表1所示.

3 结果

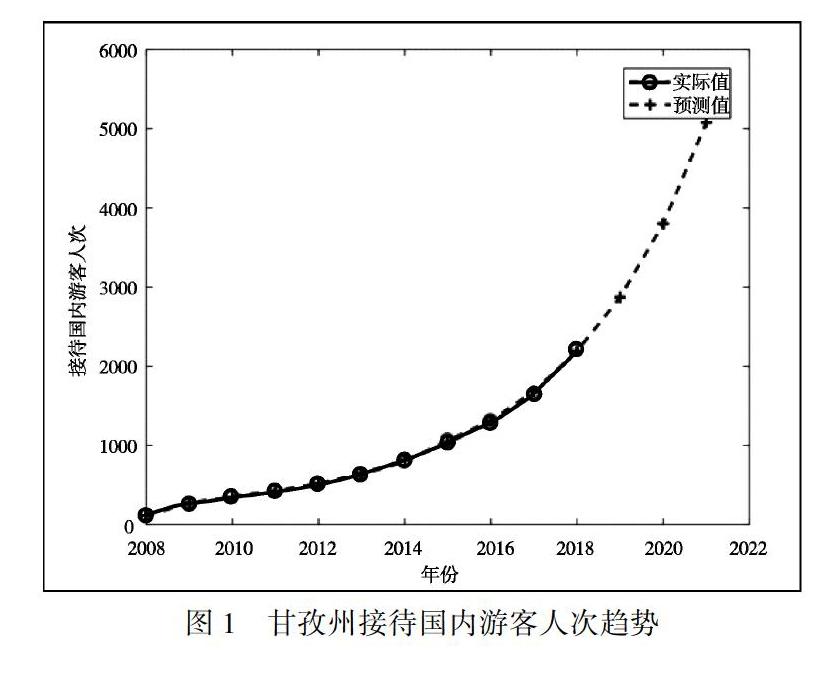
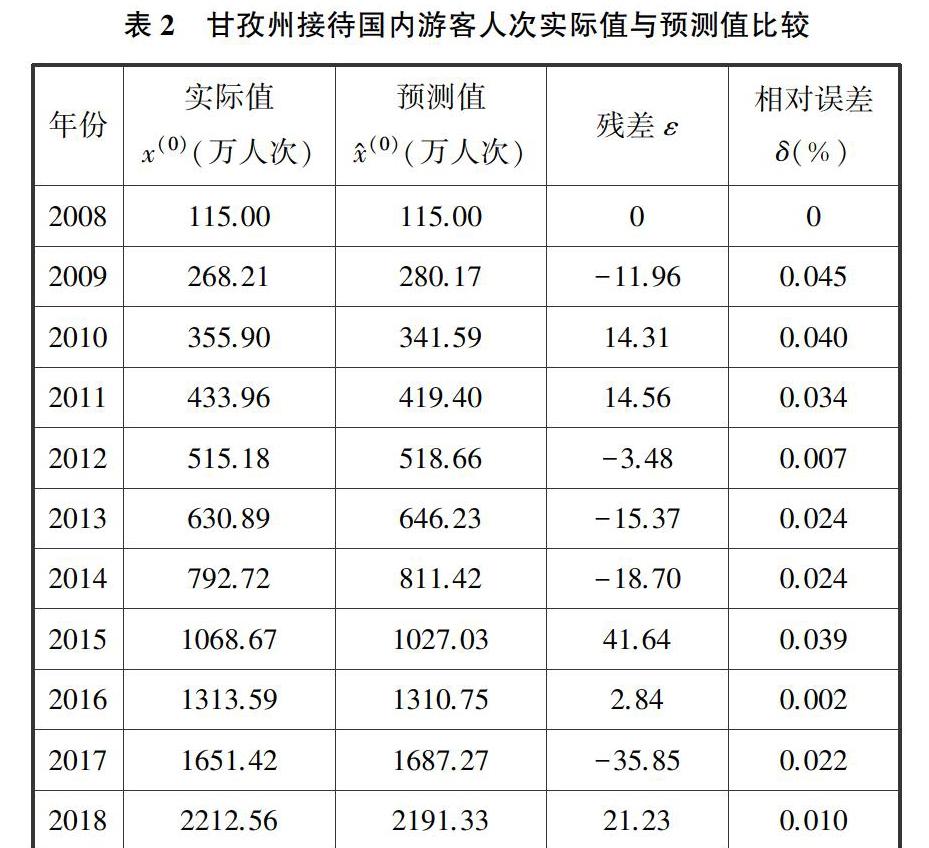
2008～2018年甘孜州接待国内游客人次原始时间序列为x（0），如果直接采用GM（1，1）模型预测，则相对误差序列中最大相对误差为14.2%，最小相对误差为0.1%，平均相对误差为5.3%，相对误差一致性较差.因此，为了提高相对误差的一致性和精度，我们对原始序列取自然對数得到y（0）=log（x（0）），对新的序列y（0）应用GM（1，1）模型得到预测序列y^（0），再对预测序列y^（0）进行还原运算得到原始序列x（0）的预测序列x^（0）=expy^（0）（如表2所示）.如表2所示，采用对数变换后应用GM（1，1）模型，相对误差序列中，最大误差为4.5%，最小误差为0.2%，平均误差为2.2%.故对甘孜州接待国内游客人次原始时间序列应用对数变换后的GM（1，1）模型提高了预测精度.

经拟合优度检验均方差比值C=0.037，小残差概率P=1，模型预测等级为1级（优）.因此该模型可以用于外推预测短期甘孜州接待国内游客人次（如图1所示）.假设不发生重大影响人们旅行计划的事件，我们用该模型预测甘孜州2019～2021年接待国内游客人次分别为2872.3万人次、3800.8万人次、5079.3万人次，总体呈上升趋势.

4 讨论

灰色预测模型是一种全因子的非线性拟合外推类方法模型.我们将甘孜州的发展变迁当作一个灰色系统，用灰色模型去发展，认识其原始时间数据序列中蕴含的内在规律，从而预测接待国内游客的发展趋势.由于甘孜州接待国内游客人次远远超过接待境外游客人次，则我们可以将甘孜州接待国内游客人次视为甘孜州接待游客人次.因此，本文数值模拟只考虑甘孜州接待国内游客人次而不考虑接待境外游客人次.由模型预测可以看出，甘孜州接待国内游客人次将保持较高增长的态势，尤其是自2017年过后增长速率明显加快.这是在提醒我们，游客人数在持续增长的情况下，旅游服务业要能够跟上.因此，该模型预测为甘孜州旅游行业和相关职能部门提供了一定的科学决策和参考意义.另一方面，灰色预测模型只能反映数据的内在规律性，不能反馈各种自然事件、社会因素对数据的影响.因此，在制定旅游发展规划和相关政策时，旅游行业和相关职能部门还应该具体考虑当地的自然、社会、环境对其的影响.

【参考文献】[1]马霞，陈娜，刑青红，原锦涛.灰色模型在新疆地区包虫病流行预测中的应用[J].周口师范学院学报，2019，36（5）：26-30.

[2]安晓红.灰色系统GM（1，1）模型在预测徐州市甲乙类呼吸道传染病发病趋势中的应用[J].江苏预防医学，2019，30（1）：33-35.

[3]官金兰，赖煜庭.基于灰色系统的房价分析与预测模型[J].清远职业技术学院学报，2019，12（2）：31-34.

[4]刘柏阳，刘立刚.灰色预测模型在区域物流成本中的应用研究[J].会计之友，2018（23）：23-26.

[5]季宇.组合灰色模型在黑土区玉米产量预测中的应用[D].长春：吉林农业大学，2018.

[6]李志勇，张成.四川省入境旅游客流量预测研究：基于灰色预测模型[J].赤峰学院学报（自然科学版），2014（22）：97-99.

[7]杨飞，张莹.吉林省入境旅游客源灰色预测模型[J].吉林工商学院学报，2012（3）：20-23.

[8]徐鸿，邓博，蒋东方，郭鹏，倪永中.基于灰色系统的过热器管壁温度预测模型[J].中国机械工程，2017，28（22）：2662-2668.

[9]刘忠贺，李宗春，何华，郭迎钢.灰色系统及线性回归模型在变形沉降中的应用[J].测绘通报，2018（S1）：262-265.

[10]胡承洪，程林林，张永韬.体育产业结构灰色评价模型与结构优化战略的探讨：以四川省为例[J].成都体育学院学报，2012，38（6）：1-8.