Python环境下π的计算精度研究

文倩 饶馨 李徐岩

【摘要】本文选取了6个π值的计算近似公式，在python环境下，根据公式编程运行得到各个公式的计算结果，并从横向、纵向等多角度进行比较.结果表明：拉马努金公式和丘德诺夫斯基公式无论在速度还是精确度上都具有极其优良的性质，其用来计算π值时所需项数最少，速度最快，计算的精确度也最大.除此之外，公式中阶数越高，分母越大，则其收敛速度越快.此结果对于测试或检验计算机的各项性能具有极大的意义.

【关键词】拉马努金;丘德诺夫斯基;莱布尼兹;沃里斯;巴塞尔问题

一、引言

π值的含义是圆周率，即圆的周长与直径的比值，在大多数科学计算中，所用的值一般不超过10位小数.然而从古至今，人们始终没有中断对更精确的π值的渴求.π的研究在一定程度上反映这个地区或时代的数学水平.德国数学家康托尔说：“历史上一个国家所算得的圆周率的準确程度，可以作为衡量这个国家当时数学发展水平的指标.”π的计算价值及研究意义主要体现在如下两点：（1）它现在可以被人们用来测试或检验超级计算机的各项性能，特别是运算速度与计算过程的稳定性;（2）计算的方法和思路可以引发新的概念和思想.本文主要对有关π值计算的精确度和复杂性进行研究，拟解决π的高精度计算，从而用于检验计算机的可靠性和对于运算、程序和算法的正确性.本文所基于的python语言具有简单易学、开源、高级语言、可移植性、解释性、面向对象、可扩展性、丰富的库以及代码可读性强等九大优势，给本文代码的编程和运行带来了极大便利.

二、π的近似计算方法及结果

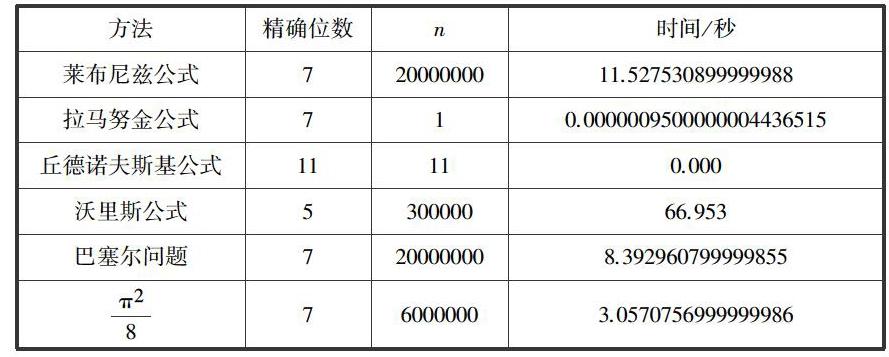
本文选取了6种π值的计算方法，在python环境下运行分别得到如下结果：

从表格和图中可以看出：

（1）对于每种计算方法，项数对精确度的影响呈递增趋势.

（2）在结果都近似到16位小数的情况下，采用拉马努金公式计算的结果精确到第16位小数时所需项数是5种方法中最少的，可见其收敛速度也是最快的.

（3）除了拉马努金公式计算方法以外，在相同项数情况下，用π2[]8法计算所能得到的精确度是余下4种方法中最大的.

（三）时间对精确度的影响

从表格和图中可以看出：

（1）对于每种计算方法，计算时间对精确度的影响呈递增趋势，这是因为当所给时间越长时，计算机能计算的项数也越多，再从前面可知，项数越多时精确度越大.

（2）拉马努金公式和丘德诺夫斯基公式在短时间内得到的精确度更高，在相同的时间内，这两种方法比其余4种方法所得的精确度高很多.

（3）除了拉马努金公式和丘德诺夫斯基公式2种方法以外，在相同时间内，用π2[]8法计算得到的精确度在其余方法中是最高的.

（四）原因分析

【参考文献】[1]韩思，朱长贵.级数收敛的速度[J].渭南师专学报，1996（S1）：39-40.