抽象概念教学要重视探究概念的生成过程

韦恺华

【摘要】新课标提出抽象概念的教学要关注概念的实际背景与形成过程.基于观察、实践、探索、思考、归纳等数学探究活动的开展，不仅能帮助学生理清概念的来龙去脉，还能使学生在探究过程中积累发现问题、研究问题的经验，从而感悟数学思想方法.

【关键词】无理数;逼近思想;数学探究活动

数学概念刻画客观事物的本质特征，很多教师在数学概念的教学中直接给出概念的定义，让学生记住定义，再花大量时间对定义进行应用.这样的教学忽视了对概念生成过程的探究，学生机械地凭记忆接受这些知识，全然不知其中蕴含的数学知识的发生过程，更难以体会到数学本身的价值，这对学生今后的数学学习以及思维能力的发展会产生不利的影响.下面笔者以苏科版七年级上册“有理数与无理数”中无理数概念的教学片段为例，阐述如何在抽象概念教学中开展一系列的探究活动，从而培养学生解决问题的能力.

一、课前思考：教学内容前置及原因分析

1.考虑学生的认知能力

学生在学习的过程中对数的认识不断更新.小学阶段他们已经接触到正数和负数的概念，知道整数包括正整数、0、负整数，分数包括正分数、负分数，且只需要在整数集合中添加“分数”就得到了“有理数”.事实上，采用这种描述外延的方式来定义有理数并不能真正揭示有理数的本质特征，而且没有明显的思维提升.其实，所有整数都可以写成分母是1的分数，因此，可以定义有理数是一切能写成分数形式m[]n（m，n是整数，且n≠0）的数.这样根据概念的本质来定义有理数，体现了知识在深度方面的提升，突出了初中数学知识与小学数学知识在思维上的不同，能加深学生对有理数本质的理解，同时为定义无理数做下铺垫，提供了方便.

2.考虑知识之间的关联

数学本质上是一个整体，不同知识之间存在着不可忽视的联系.教材在七年级下册安排了解一元一次不等式的内容，如不等式x+1>4的解集是x>3，对应在数轴上：3的位置是一个空心圈，与“3”对应的点右边的所有点表示的数都是这个不等式的解集.如果学生这时提出问题：“3”右边的数都是有理数吗？答案显然是否定的.我们知道数轴上的点对应的也可能是无理数，“3”右边的数可能是有理数，也可能是无理数.若不将无理数概念的教学前置，就无法回答学生提出的问题.

从上述两个方面分析，不难看出无理数概念的前置对学生初中阶段的数学学习是非常必要的.

二、抛出问题

在学习了有理数的定义“能够写成分数形式m[]n（m，n是整数，且n≠0）的数称为有理数”后，我们通过计算、探究发现：有限小数和循环小数都可以转化为分数，它们都是有理数.教师可以设置这样的问题——“是不是生活中遇到的所有数都是有理数呢”“有没有除了有理数以外的数呢”，激发学生强烈的好奇心，增强他们对新知识的探索欲望.

三、探究无理数概念的生成过程

在实际教学中，学生能举出π、0.3142537…等数，并有人通过运算发现这些数都不能转化成分数形式，因此它们不是有理数.学生在这一过程中积极思考，不断论证，充分锻炼了数学思维.那么，这些数到底是什么数呢？生活中有这样的数吗？教师进一步追问，引发学生积极投入思考.

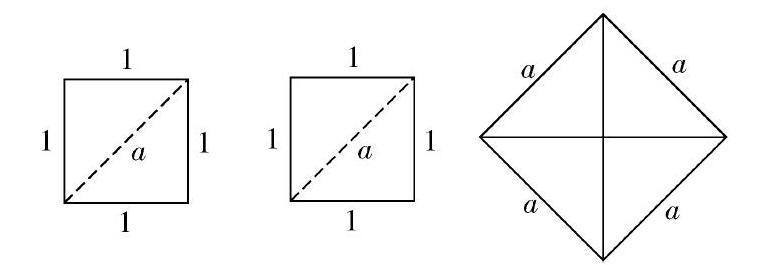
【实践】拼图游戏：请同学们拿出准备好的两个边长为1的小正方形和剪刀，将小正方形沿图中虚线剪开，设法重新拼成一个大正方形.大家动手试一试，并请一名同学把自己拼的图在黑板上展示出来.

问题：这个大正方形的面积是多少？为什么？

说明：通过拼图活动，学生可以感受无理数产生的实际背景及其存在的合理性，培养动手操作能力和合作精神.通过直观的展示及对“问题”的探究，学生培养“数学地思考问题”的习惯.对于这个问题，学生能很轻易地解决，这也会让他们对接下来的问题探究充满信心.

【探索】如果大正方形的边长为a，那么a2=2，你知道边长a是多少吗？

问题1：a是整数吗？为什么？

问题2：a是分数吗？为什么？

问题3：a是有理数吗？

说明：在实际教学中，学生通过思考、交流无法说出a具体是多少，探索活动旨在让学生认识到现实生活中确实存在他们不了解的数，发现“有理数”并不能满足实际生活的需要.对于问题1，学生能做出解答：因为12=1，22=4，所以1

【思考】根据探索活动，我们知道a不是整数，也不能化为分数的形式，说明a不是有理数，那么a到底是怎样的一个数呢？它到底有多大呢？

说明：简单的提问引发学生更深层次的思考.在实际教学中，教师要鼓励学生寻求不同的方法来探索，从而更加深入地理解无理数概念.教师引导学生进行估值，尝试通过小数运算对a进行定量研究：1.5×1.5=2.25，1.4×1.4=1.96，采用逼近的方法，得1.4

可见，a是一个无限小数，它总是介于两个有限小数之间，但永远找不到一个有限小数等于a.在这个经历数的扩充的过程中，学生不仅能感受数学的逼近思想，还可以体会“无限”的过程，发展自身的数感.

【归纳】前面提到的π是小学阶段学过的圆周率，它的值是3.141592653589….

问题1：请你说说a的值与π的值有哪些共同点，并归纳出无理数的概念.

问题2：你能写出几个也具有这些特点的数吗？

问题3：π[]4是无理数吗？为什么？

说明：问题1旨在让学生自己在探索活动的基础上归纳总结出无理数的特点“都是无限小数，且小数点后的排列无‘循环规律”，从而揭示出无理数的本质属性：无限不循环小数叫作无理数.这里将无理数概念的提出安排在对a进行定量分析后，有助于学生理解和记忆无理数的概念.而问题2则是考查学生对无理数概念的掌握情况，学生可以构造出像0.1010010001…、-0.1010010001…这样的无理数.教师在实际教学中应鼓励学生发散思维，对写出的答案进行同伴互查.问题3是实际教学中错误率很高的一道题目，学生直接观察其外在形式得出结论“这是有理数”，而忽视了有理数概念中提出的分数形式中分子、分母需是整数的要求.设置该问题是希望帮助学生认清有理数和无理数概念的本质区别，能正确识别并判断某些数是否为无理数，训练学生的思维判断能力.此题也让很多学生明白了这样一个道理：学习不能浮于表面，要透过现象看本质.

【阅读】阅读材料，了解“无理数”的发展史.

说明：教师通过讲述“无理数”的发展史，让学生了解发现无理数的曲折过程，初步了解通过数学家的不断努力，无理数的家族实际上要比有理数的家族庞大得多，逐步消除学生头脑中“无理数很少”的感觉，从而让学生体会到数学美在我们的生活中无处不在.

四、传统的无理数概念呈现方式

一般来说，讲无理数就需要讲平方根.下面笔者以上述问题中所研究的大正方形的边长a为例，简要说说如何利用反证法证明a是无理数.

假设 a是有理数，则它可以写成最简分数p[]q（p，q是整数，p与q互质）的形式，于是2=a2=p2[]q2，即p2=2q2，由于2q2是偶数，所以p也是偶数，不妨设p=2x，可得4x2=2q2，即q2=2x2，而2x2是偶数，所以q应是偶数，这样p，q都是偶数了，它们的公约数是2，与p，q互质矛盾.由此可见，a不是有理数，而是无理数，人们通常将它记为2.

说明：这里采用反证法对2是无理数进行了严格证明，可以阅读材料的方式供有兴趣的学生阅读，让部分学生初步感悟反证法的思想.

结 语

a2=2中的a是实实在在存在的数.上述对a的探究，从判断其存在性入手，到对其定性分析，再到定量分析，最终归纳总结出 a具有的属性.这种安排体现了数学学习和研究的方法，即在数的发展中，面对新的数时我们通常会提出如下疑问：它存在吗？它会是我们原先认识的数吗？它具体会是多少呢？这种数学的研究方式是推进数学不断发展的原动力，教师日常要将这种方法渗透于教学的全过程.

上面的整个探究过程充分考虑了学生的实际认知水平，巧妙地借助图形直观，通过实践、探索、思考、归纳让学生感受 a不能化为分数的形式，揭示了无理数的客观存在及其本质属性——无限不循环小数.不难看出，这比借助平方根抽象的数学运算要直观得多.“实践”中培养了学生的动手能力，“探索”中训练了学生的理性思维，“思考”中渗透了逼近思想，“归纳”中提升了学生的概括能力，“阅读”中丰富了学生的数学文化.这样的设计不仅能帮助学生掌握无理数的概念，同时能让学生在观察、比较、思考、论证的一系列思维过程中感悟数学知识，为今后进一步学习数集的扩张打下基础，培养了学生思维的有序性.

数学概念的教学不应该停留在简单地让学生去识记、让学生利用概念去解决一些实际问题的层面，而应该在教学中引导学生探究这些概念的本质，激励他们积极参与教学活动，体验概念的生成过程，从而真正理解概念，正确地应用概念.同时，教师要在概念的教学过程中激发学生的探究欲望，引导学生认识到学习数学的意义，学会“数学地思考问题”，形成解决数学问题的方法和能力，提高学生学习数学的热情.学校的数学教育不单单是传授数学知识，更重要的是对学生思维的能力进行培养.教师在课堂上引导学生经历动手实践、猜想、探究、验证、运用等完整的学习过程，不仅能培養学生对数学的兴趣，也能培养他们的合作与钻研精神，为他们今后的学习打下坚实的基础.

【参考文献】[1]万荣庆.仅仅让学生记住这些 “规定” 就够了吗？——对 “规定a0=1（a≠0）” 的教学设计与思考[J].中学数学教学参考（中旬），2010（08）：2-3.