一种基于FIFO思想的低速下无刷直流电机速度研究

付继先，杨冬娇

（1.贵州航天林泉电机有限公司，贵州 贵阳 550081；2.国家精密微特电机工程技术研究中心，贵州 贵阳 550081；3.中国航发贵阳发动机设计研究所，贵州 贵阳 550081）

0 引言

无刷直流电机的速度研究是推广其应用领域的关键技术之一[1]，此外，在速度闭环控制系统中，速度精度、速度周期决定了控制精度的理论上限。迄今为止，国内外学者对无刷直流电机的速度进行了广泛的研究[2-4]，按研究原理主要分为三类：（1）模拟研究；（2）同步研究；（3）解析研究。模拟研究是依据转速与某模拟量的关系间接获得电机转速；同步研究是采用已知频率的旋转体与电机转速同步，从而得到电机的转速；解析研究是以速度定律为准则，不同应用背景下对定律进行修正，直接得到电机转速。

钟灶生[5]等人基于电机位置传感器，将三路传感器输入CPLD进行六倍频并将其作为速度反馈信号，这极大地提高了速度计算周期，减小了速度环调节时间。然而，当电机速度低于2000r/min时，速度波动达160r/min。Chaofeng Pan[6]等人以一路霍尔信号研究电机转速，发现目标速度为300r/min时，信号进行2次滤波后，输出的速度误差依然有274r/min。很多学者[7-8]利用电机反电势对电机速度进行估算，但该技术仅应用在中、高速下电机转速的表征，这是由于电机在低速运行时，很难有效地识别反电势接差。Latha，R[9-10]等人采用自适应控制技术估算电机速度，并进行了大量的研究工作，但该技术伴随着复杂的计算，需要高速的处理器，增加了成本。研究者[11]采用精密的编码器对无刷直流电机速度进行研究，该方法速度精度高，适用范围广。然而，昂贵的编码器，占驱动系统的很大一部分比例，此外，其需要单独增加编码器，使体积进一步增大。Hui，S[12]等人采用光学反射式齿轮进行速度研究，测量精度高，传输距离长，适用于电磁干扰或传感器传感距离较宽的场合，缺点就是体积大，成本高。

综上所述，采用现有方法进行低速下无刷直流电机速度的表征，往往伴随着辅助电路复杂、体积大，结果不可靠、误差率高，速度周期长，成本高等问题。该类问题严重限制了无刷直流电机在小体积、低成本条件下的可靠应用。因此，一种新型的、可靠的、低沉本的、小体积的表征低速下无刷直流电机速度的方法是亟待解决的关键。

本研究提出了一种基于霍尔FIFO的测速思想，以霍尔传感器为位置脉冲信号，采用T法测量低速下无刷直流电机速度的新方法。首先分析了形位公差对霍尔位置传感器的影响机理；基于分析理论，研制小速度无刷直流电机控制系统；最后试验验证霍尔FIFO测速法的可靠性。研究结果为无刷直流电机应用背景的推广奠定了理论基础与技术支持。

1 理论分析

1.1 形位公差对位置传感器的影响机理分析

无刷直流电机位置传感器通常采用双极锁存型霍尔传感器。基于霍尔效应[13]，传感器法线方向上的磁感应强度的Bcos 大小决定其输出Vout电平的高低，其中B为外磁感应强度，为传感器法线与外磁感应强度方向的夹角。当Bcos 大于导通值BOP时，传感器输出低电平；当Bcos 小于释放值BRP时，传感器输出高电平，其余值保持上一个电平状态，其工作原理如图1所示。因此，有效磁感应强度的大小是影响传感器实际输出的关键。

图1 双极锁存型霍尔传感器工作原理图

电机本体中存在诸多形位公差，如转子磁极周向尺寸误差，传感器安装误差，安装板设计及安装误差，电机转子与安装板同轴度误差等。该公差导致位置传感器上的有效磁感应强度Bcos 发生变化，使传感器输出电平出现超前、滞后，间隔不相同等现象，其导致的原因分别为：（1）超前、滞后主要是霍尔传感器的中心法线与转子圆心线存在角引起的；（2）电平间隔不等是由转子圆心与安装板圆心同轴度误差，转子磁极周向尺寸误差，传感器安装误差等所致，如图2所示。

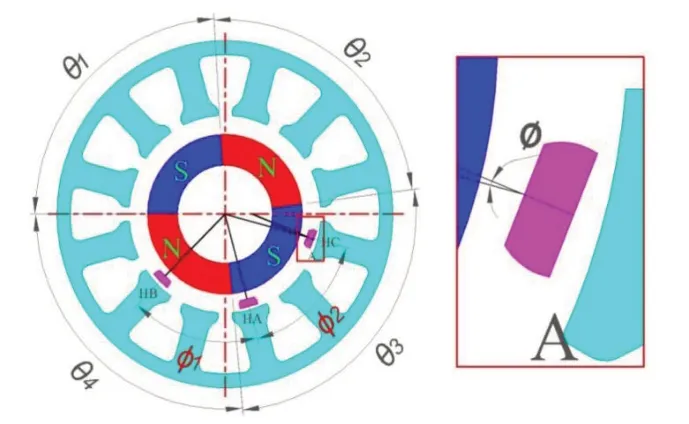
图2 4 极、12 槽BLDCM 径向剖面图

结合电磁学理论，进一步分析电机形位公差对三路霍尔位置传感器输出电平的影响，图3为4极、12槽BLDCM周向剖面图。由图可知，电机一转内三路位置传感器电平变化机械角δ和T不一致，这是由于电机转子N、S极周向尺寸1、2、3、4不等、传感器法线与外磁感线强度方向夹角导致的。此外，霍尔信号两脉冲的时间差T和机械角δ以360°机械角周期性地复现。

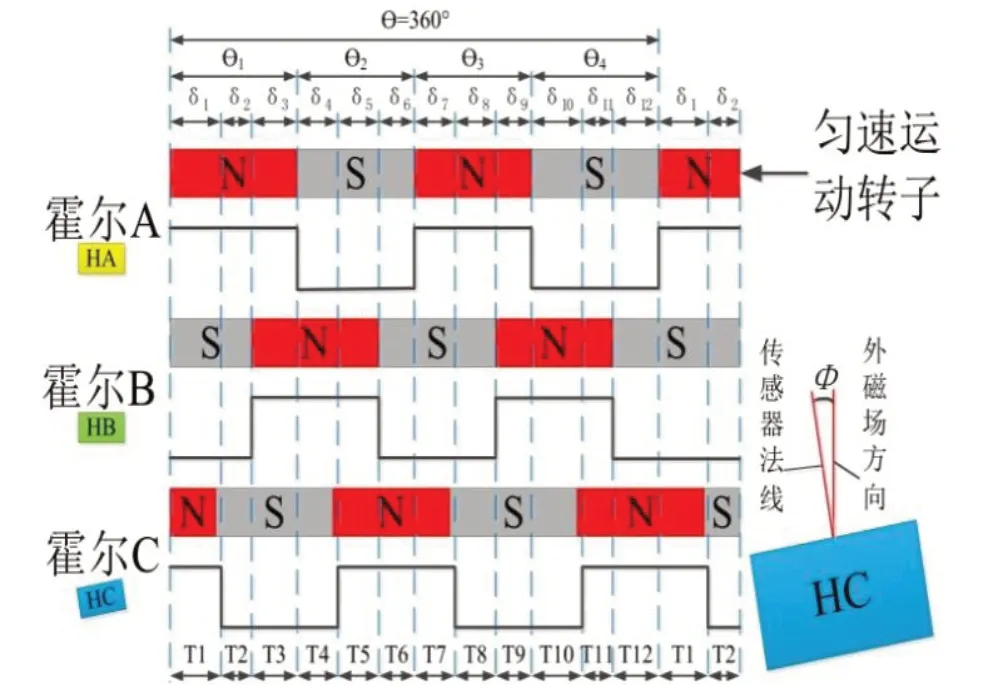
图3 4 极、12 槽BLDCM 周向剖面图

1.2 T测速法理论分析

T测速法[14]是统计物体经过间隔为 （度/°）的两个脉冲的时间 （秒/s），然后根据式（1）计算得到的值即为物体速度 。由式（1）分析可知，在两脉冲间隔已知情况下，该法得到的速度，最大误差为一个时钟计数。以频率为f的时钟为时间计数信号，则两个脉冲之间的计数差为x，最大误差为±1，误差率β由式（2）进行计算。

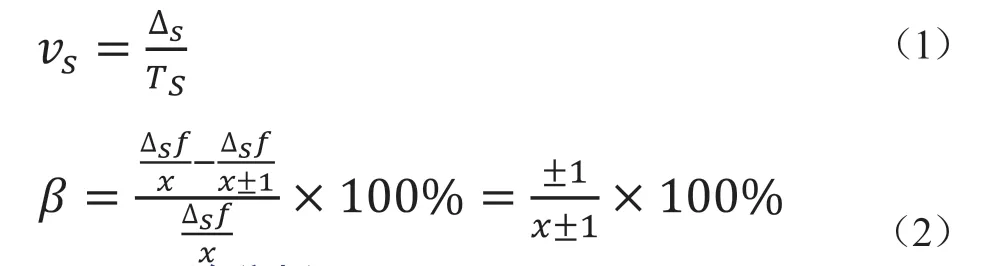
1.3 FIFO理论分析

FIFO[15]是一种具备连续缓存或者存储数据的缓存器、存储器，操作中遵循先进先的原则，其工作原理如图4所示。FIFO主要应用于跨频率之间的数据传输、不同位宽的数据匹配、数据流处理。其具有传输速率快、顺序执行不丢帧、循环时间短等特点。

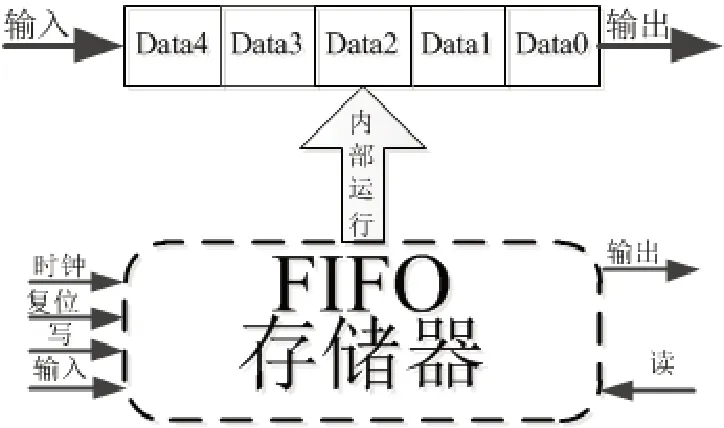
图4 FIFO 工作原理

2 控制系统研制

控制系统主要由两部分组成：（1）硬件系统；（2）软件系统。硬件系统应具备通讯、电流采样、电压采样等能力，而软件系统包括通讯、换向、测速等能力。

2.1 硬件系统研制

系统主控芯片采用ALTERA的型号为EP3C25F256I7N的现场可编程器件（FPGA），该芯片相对于DSP、MCU芯片，具有强大的并行处理和高速运算能力，特别适用于大型的计算；采用光耦TLP2105作为主控芯片和驱动电路的隔离器件，IR2110驱动芯片具有驱动能力、抗干扰能力强等优点，将其作为三相逆变桥的驱动电路。此外，ADM2582实现上位机与系统的RS422通信。硬件系统原理如图5所示。

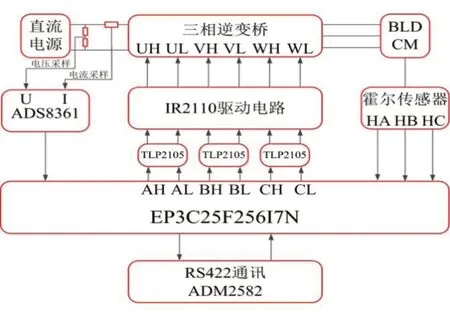
图5 硬件系统原理图

2.2 软件系统研制

采用T法研究电机转速，误差率δ主要决定两脉冲之间的时间计数差T，T越大，误差率β越小。而低速下电机的速度测量，时钟频率都是M级以上，对于计数误差为1，该方法测量结果无限接近于真实值，影响结果忽略不计。然而，很多学者采用该方法获取低速下无刷直流电机的速度，都伴随有速度更新周期长或速度误差大等现象。由上述分析可知，速度精度差主要由双极锁存型霍尔传感器输出电平对应电机机械角变化所致，速度更新周期长则是采用大机械角度引起。

因此本系统综合霍尔信号六倍（60°测速法）速度更新周期快、电机整周测速法计算速度精度高的优点，引入FIFO运行机理，提出一种基于霍尔FIFO测速法研究低速下无刷直流电机的速度。

具体流程：首先硬件系统上电初始化并捕获三路霍尔传感器的状态；其次接收上位机指令并将传感器新状态作为时间计数CNT的启停、速度计算标志，这将测速周期缩小到硬件的最小能力；接着基于FIFO先进先出的思想，将不同时间计数CNT存储于FIFO中；然后将存储于FIFO中的计数值求和并获得对应脉冲差△s；最后采用T法获得电机转速并将其输入速度调节器进行闭环。其软件执行图如图6所示。

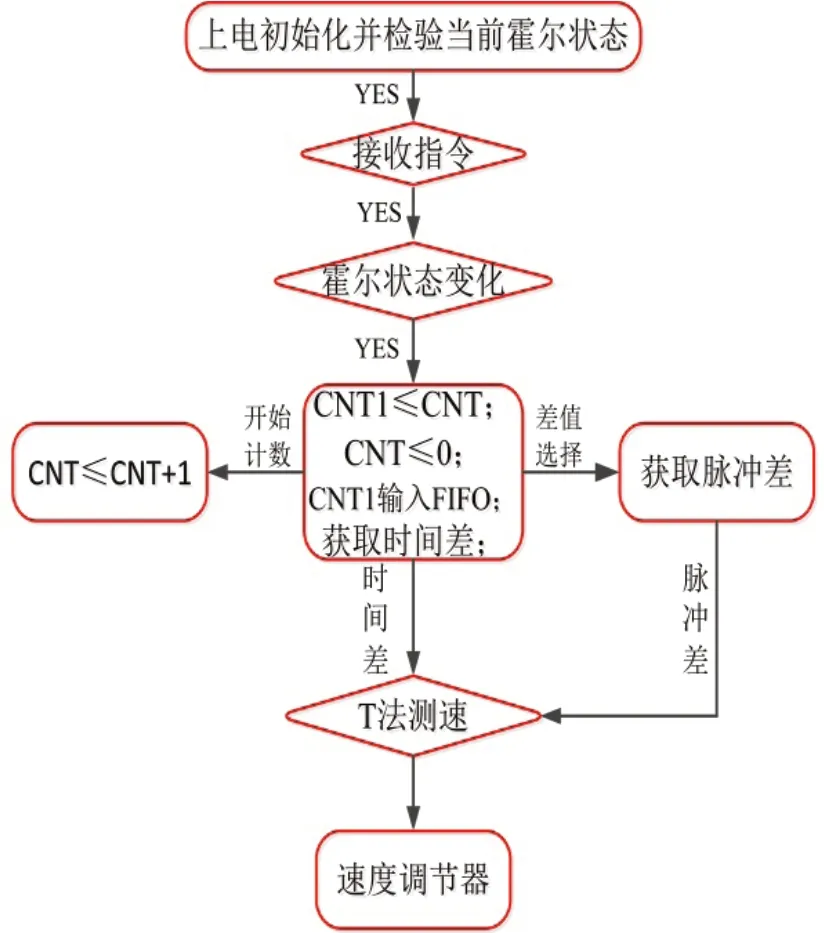
图6 霍尔FIFO 测速法软件执行图

3 试验

3.1 试验方案

本试验采用上述自研控制系统，系统中2000数字量对应100%的占空比，试验电机参数如表1所示。由预试验可知，5%是该电机在空载条件下保持连续稳定运行的最低占空比，其对应转速为60r/min。为避免其余控制参数对测速结果的干扰，试验以5%的占空比开环驱动电机。霍尔位置传感器作为电机速度计算的脉冲信号，分别采用霍尔信号6倍频（60°测速法）、霍尔信号720°（720°测速法）和霍尔FIFO（霍尔FIFO测速法）三种手段表征无刷直流电机的速度，研究结果如图5、表2所示。

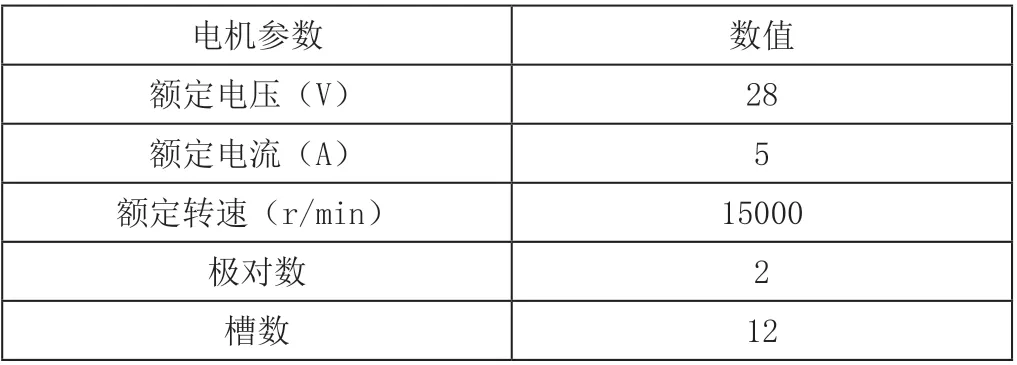
表1 无刷直流电机基本参数

3.2 试验结果

由图7可知，电机启动后，霍尔FIFO测速法获得的电机转速曲线在起始阶段快速变化，随着时间的增大而逐渐平稳；720°测速法在1100ms后，才开始计算速度，速度值偏差值较小；而60°测速法得到的速度曲线出现震荡，当电机运行1500ms后，曲线出现周期性变化，该变化是由电机霍尔传感器的安装、转子磁极不一致所引起的。60°测速法和霍尔FIFO测速法速度计算周期相同，相比于720°测速法，速度更新周期短12倍。

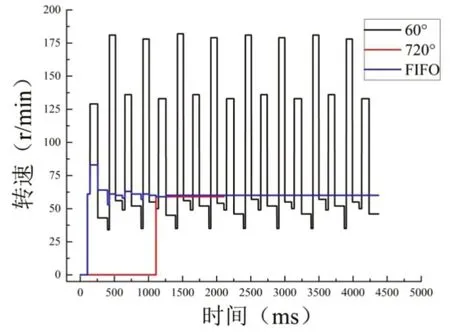
图7 不同测速法下转速对比

表2是电机运行1500ms后，三种测速方法下的误差值。由表可知，720°测速法和霍尔FIFO测速法相对误差分别为0.68%和0%，而60°测速法相对误差为58.82%；三种转速表征方式中，720°测速法和霍尔FIFO测速法得到的结果与实测结果基本相同，60°测量结果偏差最大。

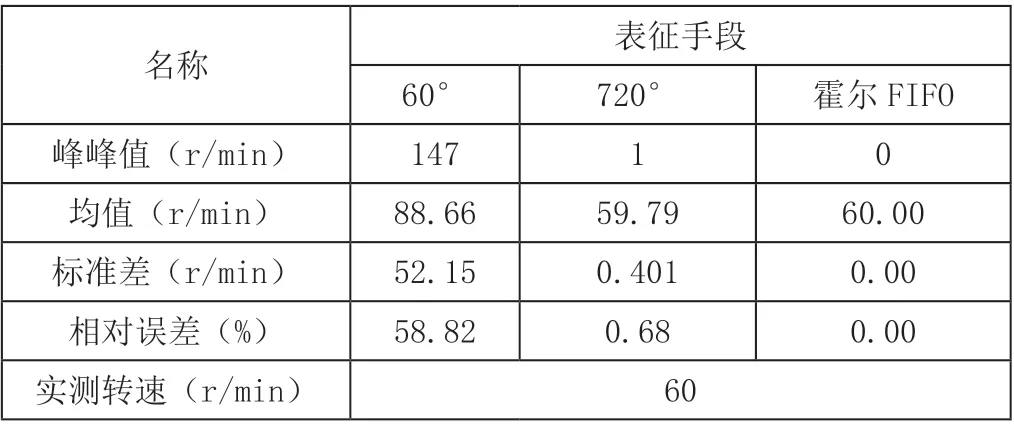
表2 不同测速法误差

4 结语

本文针对无刷直流电机低速表征难题，结合60°和720°测速法各自优势，引入FIFO理论，提出一种基于霍尔FIFO测速法来获得低速运行下无刷直流电机的速度。主要研究结论如下：

理论分析了无刷直流电机形位公差对霍尔位置传感器的影响机理，得到了电机运行一转，三路位置传感器电平变化所对应的机械角δ和T不一致，此外，两脉冲的时间差T和机械角δ以360°机械角周期性地复现；

霍尔FIFO测速法实现了低速下无刷直流电机转速的有效测量，在实际转速60r/mim的条件下，测量结果峰峰值、标准差、相对误差均为0。