重力辅助导航前沿与进展

王彤

（中国空间技术研究院，北京 100094）

潜艇等水下自主航行器在水下航行一般依靠惯性导航系统进行导航，惯性导航系统的重要组成元件是陀螺仪和加速度计，这些敏感元件测得的加速度通过对时间进行积分后可以得到速度、偏航角、位置等信息。积分过程中，误差随时间累积增大，潜艇长期在水下运行时导航精度降低。针对惯性导航系统的这一缺点，许多学者提出将重力匹配、地磁匹配、地形匹配等无源导航方法与惯性导航系统组合起来，对惯性导航进行修正。水下重力匹配技术实现的核心问题是构建全球高精度和高空间分辨率的海洋重力异常图。

测高/重力卫星、船测、航空是获得全球海洋重力场的主要技术途径，全球高精度和高空间分辨率的海洋重力异常图能有效提高水下重力匹配导航精度，但目前我国的全球海洋重力异常图空间分辨率较低，因此，需要在一定程度上对其进行插值加密，重构为高精度高空间分辨率的海洋重力异常图。由于海洋重力异常图经过插值后，空间分辨率会提升，但是，精度会降低，因此，空间分辨率和精度成反比关系（随着空间分辨率提高，精度将降低）。为了使空间分辨率与精度均满足高精度水下重力匹配导航，对重力场的插值方法的研究成为此领域的研究热点。

1 海洋重力异常图插值方法

目前，常见的海洋重力场异常图插值方法可具体分为两类，第一类为基于函数插值方法，第二类为基于统计学插值方法。函数插值方法有径向基函数插值法、曲线曲面插值法、样条函数插值法。统计学方法有克里金插值法、距离加权反比插值法、改进的Shepard插值法。距离加权反比插值是最简单的插值方法。该方法根据未知点到已知点距离加权平均值计算未知点的值。距离加权反比插值法的具体计算公式如下：

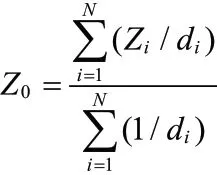
式中，Z0表示预测点的重力值，Zi表示第i个已知点的重力值，di表示第i个已知点到预测点的距离。由于插值精度较差，实际重力异常值插值过程中使用并不多。

1.1 径向基函数插值法

径向基函数插值法（Radial Basis Function， RBF）是根据已知点和基函数构建插值函数的过程。径向基函数法插值过程主要是根据已知点为位置中心求解得出插值函数的系数，从而获得预测点的值。Alessandra和Emma构造了基于径向基函数法PU内插分区方法并模拟验证该算法在重构加密海洋重力基准图方面的有效性。

1.2 样条函数函数插值法

样条插值方法是由工程制图中的样条绘图工具发展而来的。具体原理是将连续函数拼接成光滑的曲面或者曲线。其中著名的样条插值方法有格林样条函数插值法，格林样条函数插值基于最小曲率原则，以已知点为位置中心将格林函数进行线性叠加，形成插值曲面。Mardla等提出将重力值降低为重力异常值然后通过曲率连续样条函数、光滑粒子法、最小二乘配置法、克里金方法四种方法对重力异常值进行插值后能够获得高质量的海洋重力异常图。样条函数法插值后获得的格网重力场较为精确，克里金插值方法在使用适合当前区域的参数时，生成的格网重力场精度也很高。克里金法可以根据某些准则调整系数，从而能更好地自动拟合具体区域重力场的特征。

1.3 克里金插值法

克里金插值法（Kriging）是一种地质学统计方法，是最优内插法，包括简单克里金(Simple Kriging)、普通克里金(Ordinary Kriging)、协同克里金(Cokriging)和非线性克里金(Nonlinear Kriging)，其中最常用的是普通克里金插值方法。根据数据的空间相关性来加权求得未知点处的值。克里金插值法基于如下数学模型。半方差函数描述了各个点的空间关系，公式表示为：

求解克里金方程组：

估计值可以看作估计域n个已知值的线性组合

2 插值法新进展

目前，许多学者尝试用人工智能领域的方法对重力场插值方法进行完善。Sarzeaud等提出了一种基于改进的Kohonen人工神经网络的插值方法，用于将海洋重力数据插值为格网化的重力数据，最终验证改进的Kohonen人工神经网络的插值方法与克里金精度相当，并且计算时间比克里金短得多，尤其适用于当网格的大小和可用数据的数量都很大时。神经网络内插可能是将局部模型合并为全局模型的一种好方法。它不能产生异常结果，并且可以确保数据与全局模型之间的连续性。

Xu等提出压缩感知理论提供了一种信号重构方法，可以从更少的样本中恢复稀疏信号。在压缩感知理论的框架下，提出了一种基于非等宽傅里叶变换的重力数据重构方法，该方法是一种基于迭代冷却阈值法的稀疏性分析和重构算法。通过对不同采样率的二维重构试验以及与最小曲率法和克里金法的比较，表明基于非等宽傅里叶变换的二维重构方法在采样数据较少的情况下，仍能取得良好的重构效果。

3 结语

本文对目前常见的重力场插值方法拟合过程进行研究，通过分析得出结论，当使用的参数合适时，径向基函数插值方法、克里金插值方法、样条函数插值方法以及Kohonen人工神经网络等，都能获得较高精度的高分辨率重力场，这些插值方法在一定程度上会受到地形的复杂程度的影响。将神经网络支持向量机等方法和传统插值方法结合在一起，可能会提高整体的插值效率，例如，用主动学习训练克里金模型，能够提高计算效率并且保持精度。