强震作用下中庭式地铁车站灾变机制研究

赵慧玲 罗雨泽 胡定成

（上海大学土木工程系，上海200444）

0 引 言

地下结构在多个领域都有着关键的作用，因其重要性，很多研究者都对地下结构的抗震性能进行了研究［1-2］。城市地下轨道交通的快速发展，大跨度、高断面、宽柱距、异形柱等各种特色的地铁车站结构形式陆续出现，异形车站结构在地震作用下的传力机制、地震响应、薄弱环节等均不同于标准断面地铁车站结构，为探究其动力响应规律，已有学者针对异形结构开展抗震性能研究。陈苏［3］针对土-变截面地铁车站结构进行了三维非线性地震反应分析，结果表明，上宽下窄形变截面结构的下层地震响应大于上层，上层中柱的应力峰值最大。陈磊［4］针对三拱立柱式地铁车站的地震动力反应分析发现，立柱底部为最危险部位，结构外墙损伤次之，两侧副拱较中间的主拱损伤程度较低。彭晓晖［5］针对无柱大跨地铁车站的地震响应分析表明，中板地震响应最大，左右侧墙次之；顶板与侧墙的残余变形较大。吴秉林［6］针对大体积浅埋Y型柱地铁车站的振动台试验研究发现Y 型柱分叉点处、柱下端中间部位是车站结构的抗震薄弱环节。

中庭式地铁车站是为满足建筑开放式、透视化空间效果的新型车站结构形式［7］。为引入自然光，车站结构去除顶板与中板绝大部分区域；结构左右两侧侧墙仅依靠顶板连梁、中板连梁连接；为最大化空间有效利用率，顶板与中板之间的地下一层不设柱，采用无柱式结构；地下二层取消了常规的方柱，采用隐藏于屏蔽门间的薄壁柱结构，形成大跨梁-板-墙结构，荷载传递路径不同于标准断面车站。中庭段车站顶部几乎无覆土，无法形成土拱效应，属于超浅埋地下结构，周围岩土介质对结构的约束较弱。上述特征使得中庭式地铁车站的地震响应与传统标准断面、已有异形地铁车站均存在显著差异。欧飞奇等［8］对中庭式地铁车站进行了设防与罕遇烈度地震作用下的动力时程分析，表明罕遇地震作用下中柱柱端、中庭段横梁端以及板墙相接处较易进入塑性变形状态。赵慧玲等［9］通过振动台试验研究小震作用下中庭式车站结构的地震动力响应。然而，我国位于地震活跃地带，地震地面运动具有不确定性，按照相关设计规范的地震动参数区划无法完全规避地震的影响。事实表明，即使在低烈度区也发生了许多灾难性的大地震，如我国1976年唐山地震和2008年汶川地震的震中烈度高达11 度。因此，有必要针对这种中庭式地铁车站，研究强地震作用下结构的损伤累积效应，获得其灾变过程与破坏模式，从而为结构抗震优化设计提供参考依据。

本文采用有限元分析软件ABAQUS 建立土-结构三维有限元模型。基于混凝土塑性损伤模型，进行动力弹塑性时程分析，采用基于构件层次的损伤指标，研究强地震作用下中庭式地铁车站各构件的损伤发展过程，分析结构的灾变机制。

1 中庭式车站结构布置

本文以上海某典型地下两层中庭式地铁车站结构为研究对象，车站中庭段顶部两侧局部有绿化覆土，平均埋深1.5 m，顶板和中板中部开孔，地下一层不设柱，地下二层设扁柱。车站结构布置沿纵向发生变化，顶板连梁间距为11.1 m，中板连梁间距为22 m，底层柱间距为7.6 m。沿纵向取66.77 m长的结构为计算分析对象。

如图1 所示为该地铁车站横断面图。结构宽21.54 m、高15.89 m。结构地下一层的顶板连梁断面尺寸为1.5 m×1.0 m；地下二层中板连梁断面尺寸为3.5m×0.8m，孔两侧中板厚0.8 m，底板厚1 m，地下二层扁柱断面尺寸为0.3 m×3.04 m；侧墙厚1 m。

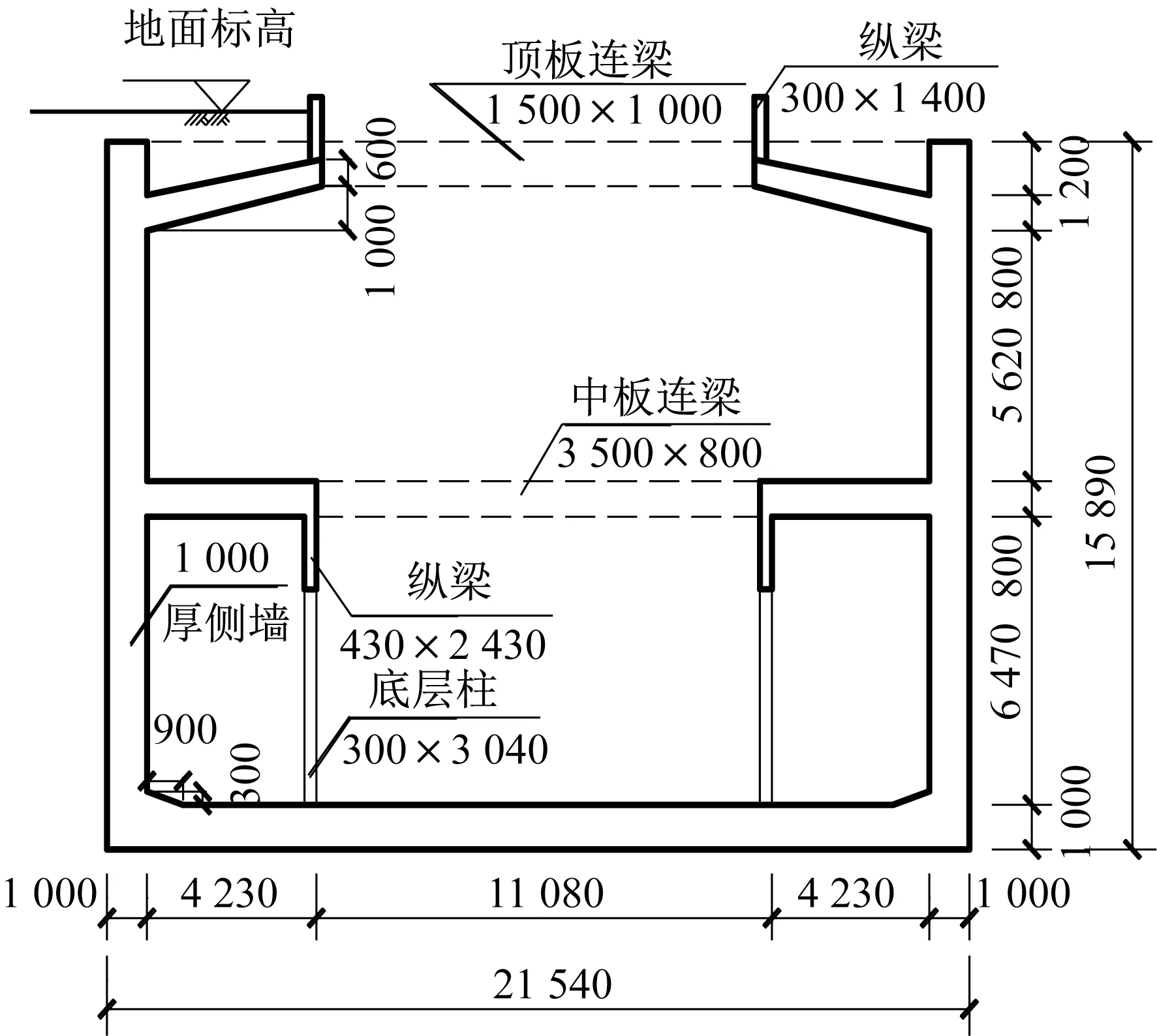
图1 车站横断面尺寸图（单位：mm）Fig.1 Cross-sectional dimension drawing of the station（Unit：mm）

2 土-结构三维弹塑性有限元模型

根据《城市轨道交通结构抗震设计规范》（GB 50909—2014），土-结构模型横剖面中土体侧向宽度在结构外延伸5倍结构宽度。土体深度取70 m，土体的几何尺寸X、Y、Z向分别为236.3 m、66.7 m、70 m，如图2所示为土-结构有限元模型图。

地铁车站混凝土等级采用C35，本构模型为塑性损伤模型，膨胀角取30°，流动势偏移值取0.1，双轴极限抗压强度与单轴极限抗压强度比fb0/fc0取1.16，拉伸子午面上和压缩子午面上的第二应力不变量之比Kc取0.666 7，黏性系数取0.000 5。密度为2 500 kg/m3，弹性模量为31.5 GPa，泊松比为0.2。钢筋采用双折线模型，平台段应力值为360 MPa。钢筋密度为7 800 kg/m3，弹性模量为200 GPa，泊松比为0.3。土的本构使用摩尔库伦模型，参数见表1。考虑土和结构的相互作用，两者之间采用摩擦，法向接触采用“硬接触”，切向接触采用库伦摩擦模型，摩擦系数取0.4。模型顶部为自由表面，底部施加纵向和竖向的位移约束。模型两侧边界为约束竖向位移并连接无限单元消除动力边界效应的影响，在模型底部施加加速度时程。

图2 土-结构三维有限元模型Fig.2 Three-dimensional finite element model of soil-structure

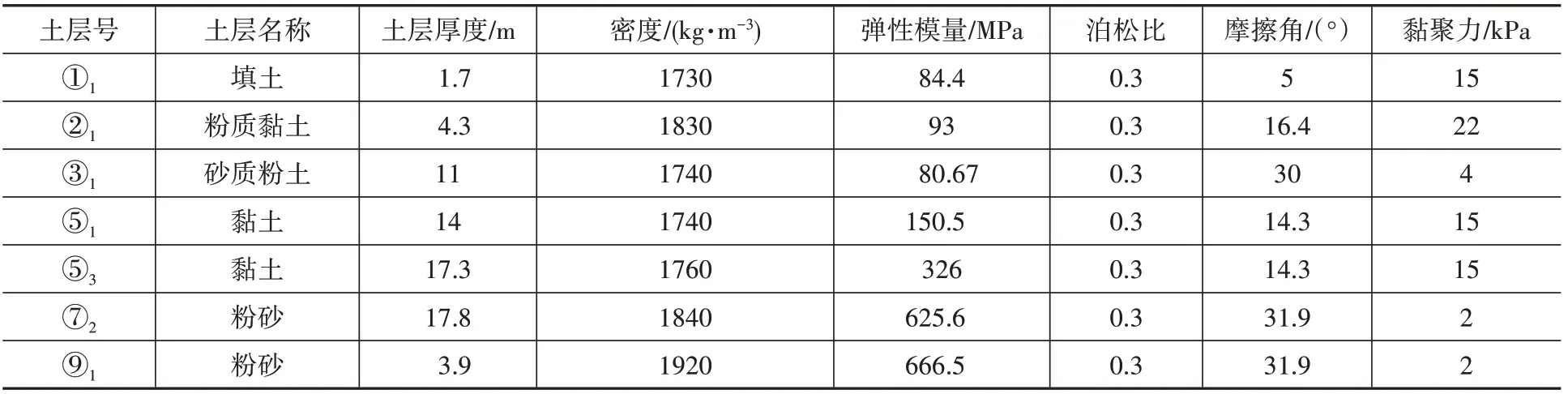
表1 土层参数Table 1 Soil parameter

地震动输入采用的地震波为Loma 波和Christchurch 波，如图3所示。对Loma波峰值调幅为0.2 g、0.3 g 和0.4 g，Christchurch 波峰值调幅至0.4 g。两者持时相近。Loma 波傅氏主频为1.6 Hz，Christchurch 波傅氏主频为0.4 Hz，相对来说，Loma 波为高频波，Christchurch 波为低频波。由于地震动特性对结构灾变的影响主要以幅值、频谱、持时三个方面。本文探究高低频两类地震动对结构灾变的影响，选择上述两种地震波来代表高低频地震动，适合用于研究。

地震波以加速度形式从土-结构相互作用模型底面输入，地震作用由模型边界，即地面以下70 m 深处的土体边界输入加速度时程，由土体传递给车站结构。

3 结构灾变过程分析

3.1 单元损伤指标

对于实体单元的结构模型中，混凝土材料的塑性损伤模型见图4。以受压损伤为例，当材料处于弹性状态时混凝土弹性模量为E0，应力超过屈服应力后，混凝土刚度退化，按照（1-dc）E0的退化刚度卸载［10］。受压损伤因子计算见式（1），其中ηc为塑性应变ε~plc占非弹性应变ε~inc的比例。实际计算中，通过有限元分析软件ABAQUS 能够直接输出单元的受压及受拉损伤因子。

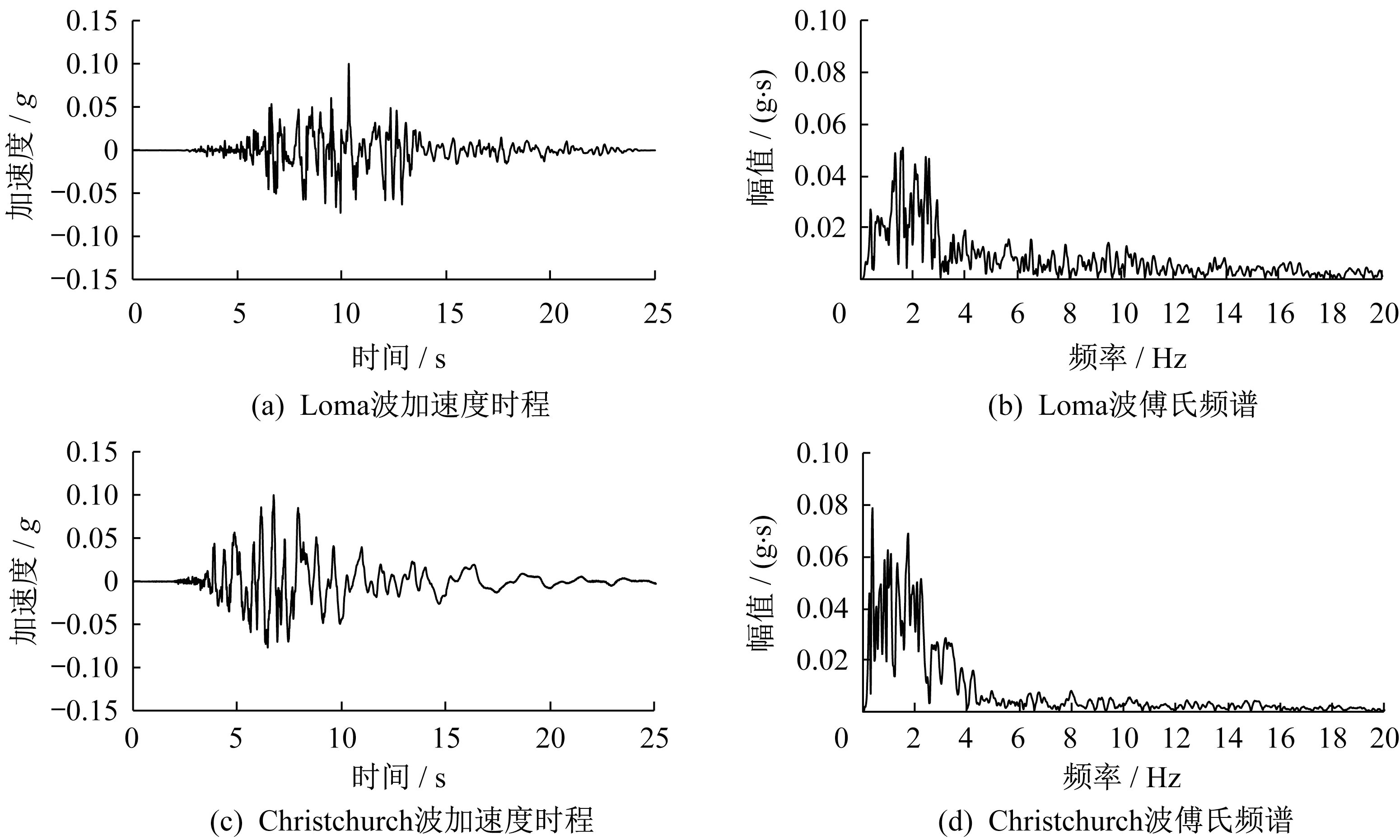
图3 各地震波加速度时程和频谱Fig.3 Acceleration time history and spectrum of each seismic wave

图4 ABAQUS混凝土塑性损伤模型Fig.4 ABAQUS Concrete damage plasticity model

3.2 构件损伤指标

基于单元损伤指标可获得结构单元的损伤发展，但难以有效评价各个构件的损伤程度。本文采用构件的损伤指标［11］来量化评价结构的损伤发展。对于结构的不同构件，易于破坏的区域为端部或跨中，沿构件纵向取其1 倍构件截面高度作为有效损伤区来计算损伤均值和损伤度以反映结构损伤程度。采用式（2）计算受压损伤均值，选取有效损伤区内每一个单元，对每个单元损伤因子进行加权平均得到有效损伤区的损伤均值。其中dCi为有效损伤区内单元i的受压损伤因子，Vi为单元i的体积。

由于结构在地震作用下，受拉和受压损伤同时存在，用单一的受拉损伤或受压损伤不够全面反映结构损伤程度，因此本文用损伤度Dg，计算方式见式（3），其中DC为该截面内受压损伤均值，DT为该截面内受拉损伤均值。

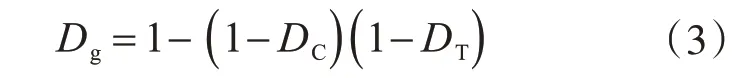
3.3 结构实体单元损伤发展过程

中庭式车站混凝土结构的损伤以受拉损伤为主。图5 为结构单元在0.4 g Loma 波作用下不同时刻受拉损伤云图。

5.48 s 时刻，受拉损伤首先出现在结构侧墙底部和底板中部处的单元。7.64 s 时刻，顶板连梁端部、中板连梁端部、中板与侧墙交界处、底板与侧墙交界处等部位的单元出现新的受拉损伤。11.36 s 时刻，顶板连梁端部、中板连梁端部和中板与侧墙交界处受拉损伤发展分布于整个构件截面，同时底板与柱底交界处单元出现新的受拉损伤。

图5 0.4 g Loma波中庭式车站受拉损伤Fig.5 Tensile damage of atrium metro station under the action of 0.4 g Loma wave

3.4 结构不同构件的损伤发展过程

根据以上出现的损伤部位，基于本文的构件损伤指标，量化计算Loma波加载下不同时刻结构各构件的损伤，如图6 所示。5.48 s 时刻，底板中部、侧墙底部损伤度达到0.22。至7.64 s 时刻，这两处损伤度增大至0.23，而顶板连梁端部、中板连梁端部、中板与侧墙交界处以及底板与侧墙交界处 损 伤 度 分 别 达 到0.41、0.25、0.22、0.22。至11.36 s 时刻，顶板连梁端部、中板连梁端部和中板与侧墙交界处损伤度分别达到0.51、0.33、0.33，底板与柱底交界处损伤度为0.14。Loma 波输入完成后结构损伤度与11.36 s时刻相同。

图6 不同时刻结构内各部位损伤度分布图Fig.6 Distribution of damage degree of various parts of structures at different times

可见，结构在Loma波作用下损伤出现顺序为侧墙底部、底板中部、顶板连梁端部、中板连梁端部、中板与侧墙交界处、底板与侧墙交界处、底板与柱底交界处。而地震动输入完成后，结构各部位损伤程度由大到小排序为顶板连梁端部、中板连梁端部、中板与侧墙交界处、侧墙底部、底板中部、底板与侧墙交界处、底板与柱底交界处。因此，顶板连梁端部为结构最薄弱位置。

3.5 不同地震波作用下结构损伤对比

图7 为0.4 g Christchurch 波加载完成后损伤度分布图。通过图7 与图6（d）的对比，发现在Loma 波与Christchurch 波两种不同地震动作用下，结构出现损伤的位置相似，都以顶板连梁端部损伤最为严重。峰值相同、持时接近的情况下，Christchurch 波对结构造成了较大的损伤。Christchurch 波与Loma 波输入时，底板与柱底交界处最大损伤度分别为0.3和0.14，顶板连梁端部损伤度分别为0.57、0.51。但是结构整体损伤分布差异较小。由于低频波通常会伴随较大的位移幅值，使得土层产生较大的变形［12-13］。两种地震动的特性中，傅氏主频有明显差距。Christchurch波输入下，结构损伤度相对较大的原因为该地震动的傅氏主频相对较低。

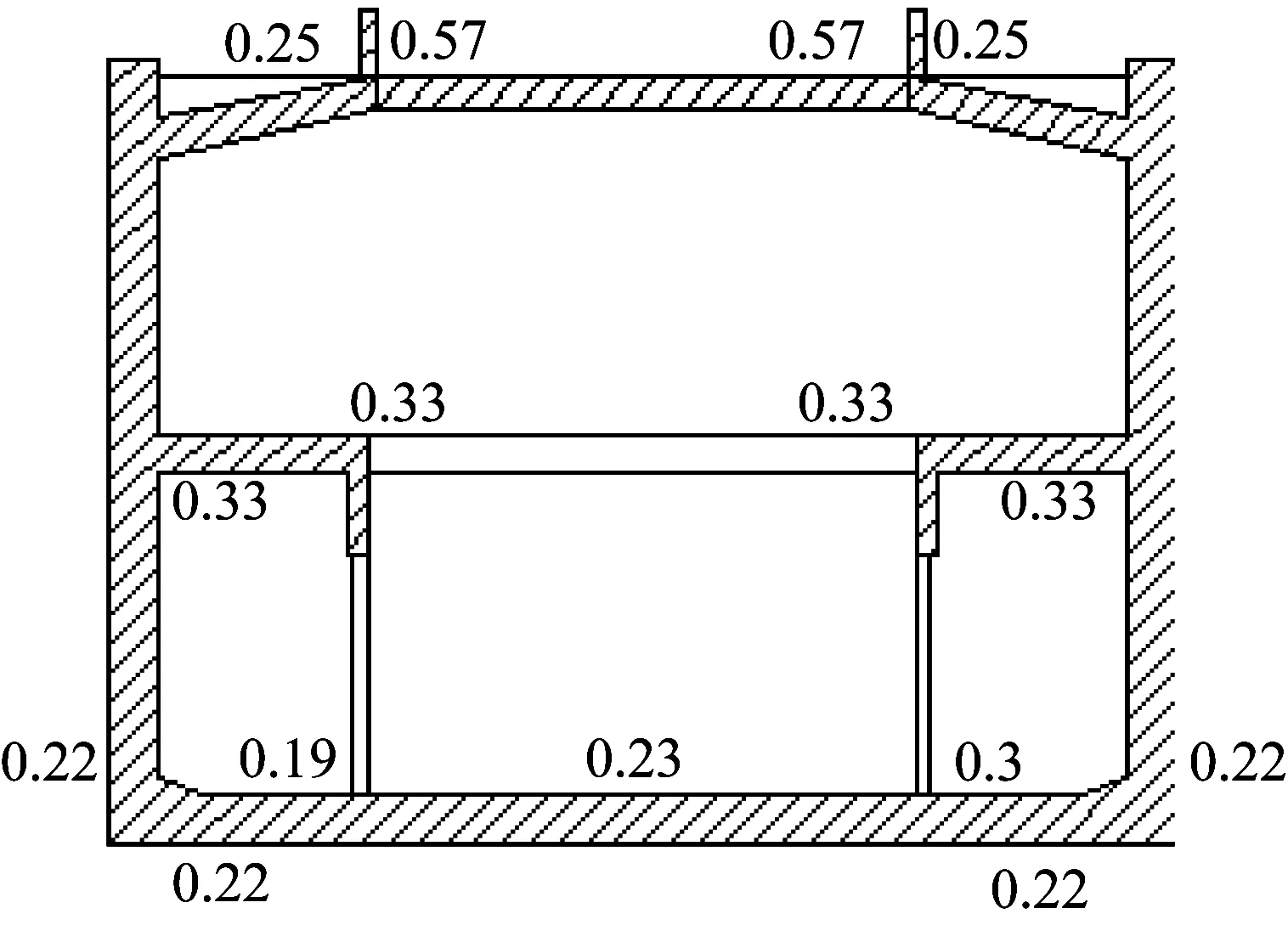
图7 Christchurch波加载结束时结构损伤度分布图Fig.7 Damage degree distribution at the end of Christchurch wave loading

4 顶板连梁破坏机理

由分析知顶板连梁为结构薄弱部位，取该构件截面进行内力分析。图8 为0.1 g、0.2 g、0.3 g、0.4 g峰值Loma波作用下不同时刻顶板连梁弯矩-轴力点与弯矩-轴力承载力曲线对比图，其中轴力以压为正。

地震动峰值为0.1 g、0.2 g、0.3 g、0.4 g时，顶板连梁弯矩最大值分别为1 700 kN·m、2 954 kN·m、3 824 kN·m、4 807 kN·m，达到抗弯承载力极限的28%、48%、62%、79%，峰值0.4 g 工况较0.1 g 工况弯矩增幅为182%，0.4 g Loma波作用下，顶板连梁截面的弯矩与压力值均位于承载力曲线内。如图8（a）所示，0.1 g 峰值时，地震作用较小，由于自重作用的贡献，顶板连梁下表面受拉、上表面受压，表现为截面内弯矩始终为正。峰值增大到0.2 g、0.3 g、0.4 g 后，地震作用下顶板连梁出现反向受弯，即截面内弯矩出现负值，随峰值增大反向弯矩值增大，如图8（b）、（c）、（d）所示。

图9 为0.4 g Christchurch 波工况下不同时刻顶板连梁弯矩-轴力值与相应的承载力曲线图。图9与图8（d）相比，峰值相同情况下，Christchurch波作用下顶板连梁轴力峰值为Loma 波的2.2 倍，弯矩是Loma 波的1.9 倍，Christchurch 波比Loma波导致了顶板连梁更大的内力响应。Christchurch 波工况下顶板连梁轴力、弯矩最大值分别达到7 402 kN、9 158 kN·m，超出了顶板连梁截面的弯矩-轴力承载力曲线范围，说明此时截面抗震承载力不满足要求。

在地震动作用下，结构内不同构件的内力响应受地震动频谱特征影响显著，低频地震动使得中庭式地铁车站结构的薄弱部位顶板连梁产生了过大内力响应。因此，构件截面的抗震设计应充分考虑不同地震动的频谱特性差异产生的过大内力响应。

5 结 论

（1）对土-中庭式地铁车站结构相互作用模型输入0.4 g 峰值Loma 波，采用基于构件层次的损伤度来量化结构构件的损伤程度，获得不同时刻结构的灾变发展过程，发现顶板连梁端部为其结构抗震最薄弱部位。结构设计时，需要对该处采取必要的抗震措施和结构优化。

（2）Christchurch波与Loma波两种工况下，结构整体损伤分布差异较小，车站结构各部位的损伤度由大到小均依次为顶板连梁端部、中板连梁端部、中板与侧墙交界处、侧墙底部、底板中部、底板与侧墙交界处、底板与柱底交界处。Christchurch波输入下，结构损伤度相对较大的原因为该地震动的傅氏主频相对较低。

图8 不同峰值Loma波工况顶板连梁弯矩-轴力与承载力曲线对比图Fig.8 Comparison of bending moment-axial force and bearing capacity curve of roof beam under different peak Loma waves

图9 0.4 g Christchurch波工况顶板连梁弯矩-轴力与承载力曲线对比图Fig.9 Comparison of bending moment-axial force and bearing capacity curve of roof beam under 0.4 g Christchurch waves

（3）地震动峰值较小时，顶板连梁弯矩为正；随着地震动峰值的增大，顶板连梁内出现了反向受弯现象。Christchurch 波工况下，顶板连梁的弯矩、轴力内力响应显著高于Loma 波工况，这与Christchurch 波主频较低相关。薄弱构件截面的抗震设计应充分考虑不同地震动的频谱特性差异产生的过大内力响应。