设置支撑的广义Maxwell阻尼耗能系统非均匀非平稳地震响应分析

李创第 王博文 昌明静

（广西科技大学土木建筑工程学院，柳州545006）

0 引 言

地震整个过程，一般都是非平稳随机过程［1］，具有频率和强度的非平稳随机特性［1］，目前地震的非平稳随机响应分析大多受限于均匀调制随机激励情形，非均匀非平稳激励的研究正日益受到国际学术界与工程界的高度重视［2-4］。因此，研究非均匀非平稳随机地震响应分析具有十分重要的实际意义。平稳激励是研究非均匀非平稳随机地震的基础，其激励模型主要有白噪声激励模型［5］、Kanai-Tajimi 模型［6］、Clough-Penzien 模型［7］、胡聿贤模型［8］等，其中Kanai-Tajimi 地震激励模型具有符合地震动特点和表达式相对简单的特点而受到广大科研人员的研究［9］。

减震工程中，为减小结构体系的地震动响应，通常采用增加结构阻尼的方法，其中黏弹性阻尼装置可以有效提供阻尼被广泛采用［10］。描述黏弹性阻尼器的力学模型主要有Maxwell［11］、GHM［11］、分数导数［11］、Kelvin［11］等，以Maxwell 模型基础可扩展为拟合精度较高的广义Maxwell 阻尼器模型，对于工程上实际应用的线性流体黏弹性阻尼器和线性固体黏弹性阻尼器，其本构关系均可用参数足够多的广义Maxwell 模型精确表示，且广义Maxwell 模型对流体和固体黏弹性阻尼器本构关系的实验数据拟合精度均优于分数导数模型和Shen and Soong 模型。因此采用广义Maxwell模型分析黏弹性耗能结构的动力性能具有较好的工程应用价值。

在实际工程中，阻尼器需要与支撑串联安装［12］，我国《建筑抗震设计规范》［13］通过限制支撑的最小刚度，以确保支撑与阻尼器串联系统发挥或接近纯阻尼器的功效，故耗能系统响应分析要考虑支撑的影响［14］。由于地震的非平稳随机特性，地震发生会首先引起支撑、阻尼器等结构保护系统的破坏，进而导致结构体系的损伤甚至毁灭，目前相关规范明确要求耗能减震系统构件在结构设计基准期内应具备足够的变形、耗能能力和良好的抗震动力可靠度［13-14］，故结构及结构保护系统响应方法的建立，对于分析抗震动力可靠度和抗震设计方法的建立具有重要价值。

针对结构响应的功率谱密度计算方法，林家浩提出了高效的虚拟激励法，将非平稳振动分析转化为简谐振动分析和确定性时间历程分析，在计算步骤简化的基础上仍保持理论上的高度精确性［15］。该方法被广泛应用于结构动力响应、风工程、海洋工程、偏微分方程的求解等众多领域［16］，但是目前关于设置支撑的黏弹性阻尼器耗能减震结构基于虚拟激励法的非平稳响应分析尚未建立。

钟万勰提出的精细积分法，对于计算机求解指数矩阵的精度有显著的提高，能有效降低因精细划分所引起的误差［17］；这种积分方法虽然不是提供解析解公式，但其数值计算结果却是高度准确的［18］。目前林家浩提出了简谐、多项式简谐、指数简谐型精细积分格式，已应用于无阻尼器结构的均匀非平稳随机响应高效分析［19］，但仅对于特定形式的激励效率较高，对于较一般的均匀与非均匀调制型非平稳随机地震激励具有一定的局限性。

本文为建立黏弹性耗能结构及其保护系统的抗震分析与设计方法，对设置支撑的广义Maxwell阻尼耗能系统随机地震响应的数值分析方法进行了系统研究。首先，采用设置支撑的广义Maxwell阻尼耗能系统进行建模；然后，基于高效的虚拟激励法，获得了非均匀的精细积分较一般精确格式，最后解出广义Maxwell 阻尼耗能系统的均匀与非均匀非平稳地震响应方差，通过算例验证本文方法的正确性，为黏弹性阻尼耗能系统在非均匀非平稳地震激励下的响应分析提供了方法。

1 结构运动方程

1.1 广义Maxwell阻尼器模型的本构关系

设广义Maxwell阻尼器受力为PQ(t)，如图1所示，其中标准Maxwell 阻尼器单元的个数为n，阻尼器的平衡刚度为k0，阻尼器第i个阻尼单元的刚度和阻尼分别为ki和ci，阻尼器相对于地面位移为xQ。

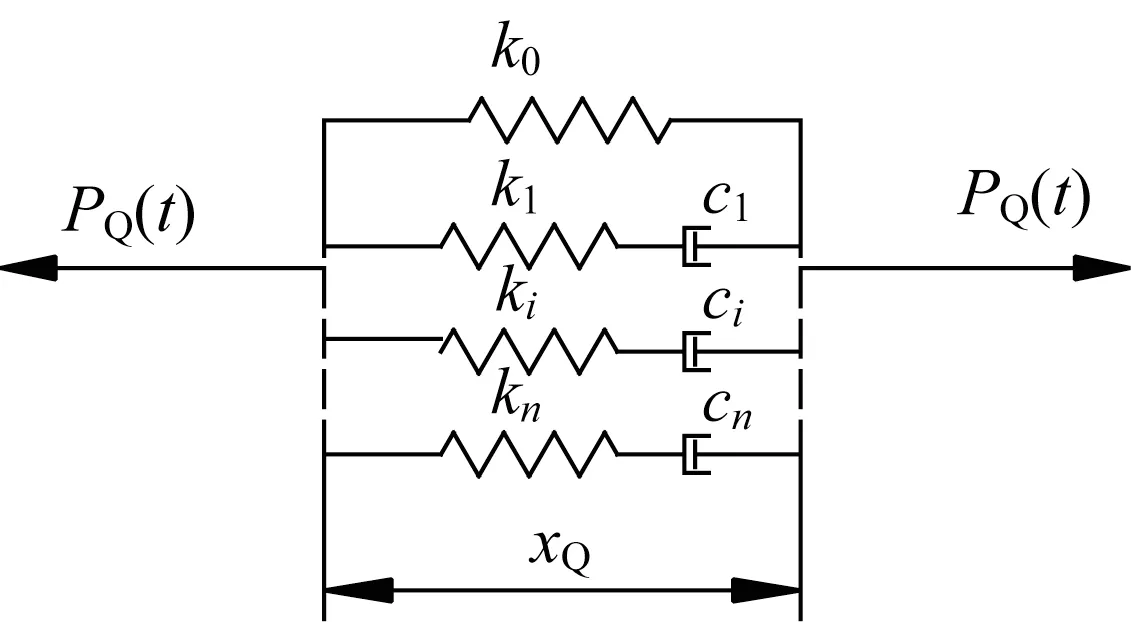
图1 广义Maxwell阻尼器模型Fig.1 General Maxwell damper model

那么阻尼器受力可表示为［10］：

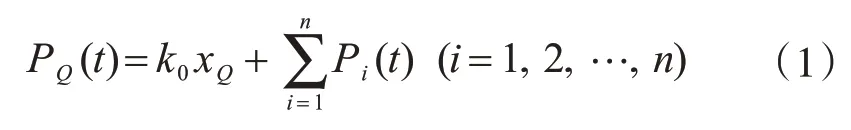
式中：

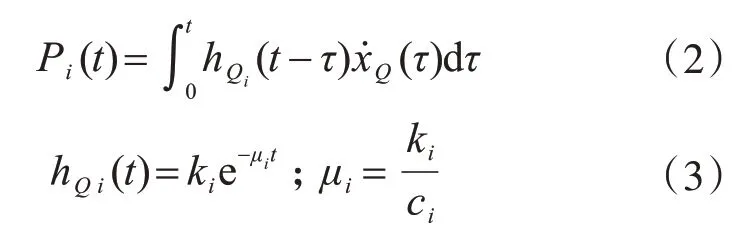
Pi(t)、hQi(t)、μi分别为阻尼器第i 个阻尼单元的阻尼力、松弛函数、松弛时间倒数。

由式（2）和式（3），可得：

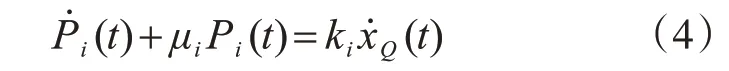
1.2 支撑与阻尼器的关系

工程实际中阻尼器一般与支撑串联安装，以产生更好的减震效果，如图2 所示，支撑刚度为kb，支撑相对于地面位移为xb，结构相对于地面位移为x。

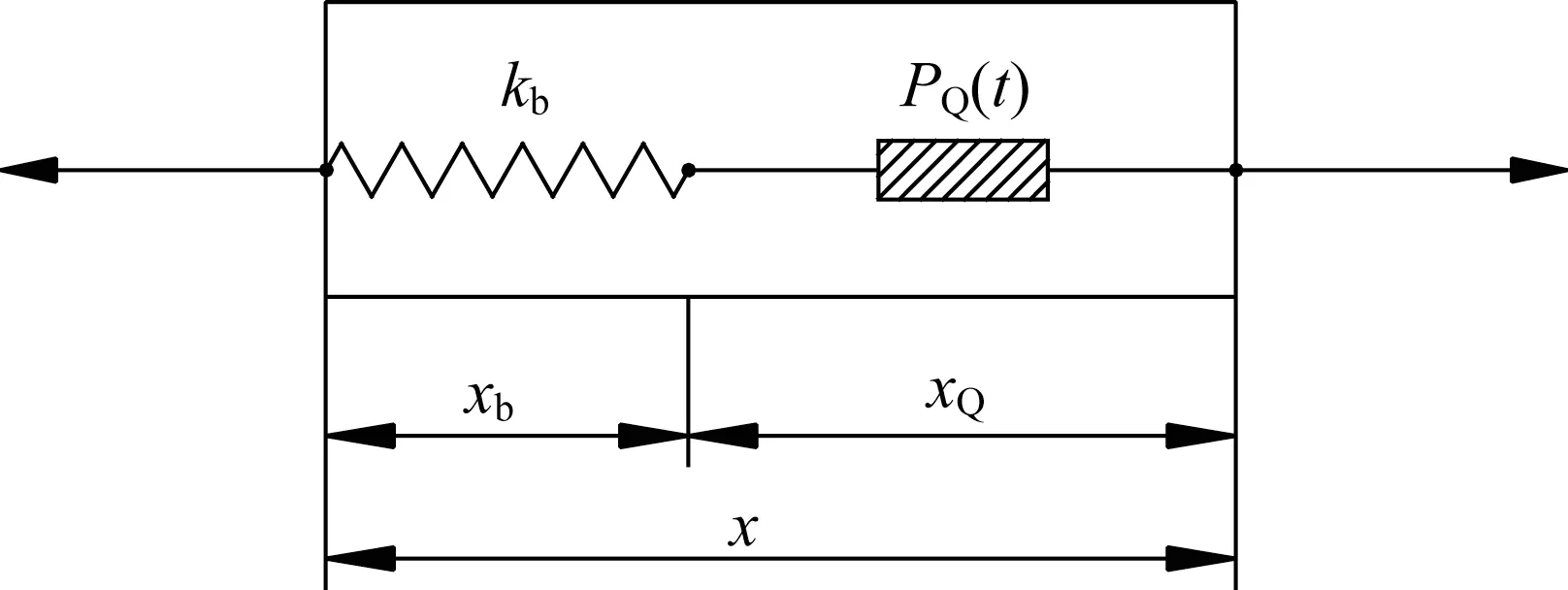
图2 设置支撑的广义Maxwell阻尼器模型Fig.2 General Maxwell damper model with support

那么支撑位移xb与结构位移x、阻尼器位移xQ之间的关系为

设支撑的受力为Pb(t)，由于串联安装故支撑受力与阻尼器受力PQ(t)相同，即

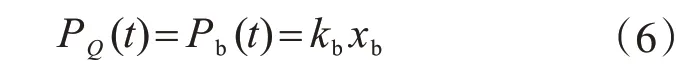
1.3 结构运动方程的建立

如图3 所示，设单自由度设置支撑的广义Maxwell 阻尼减震系统质量、刚度、阻尼分别为m、k、c，在地震动激励作用下，结构运动方程可表示为

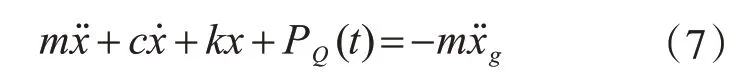
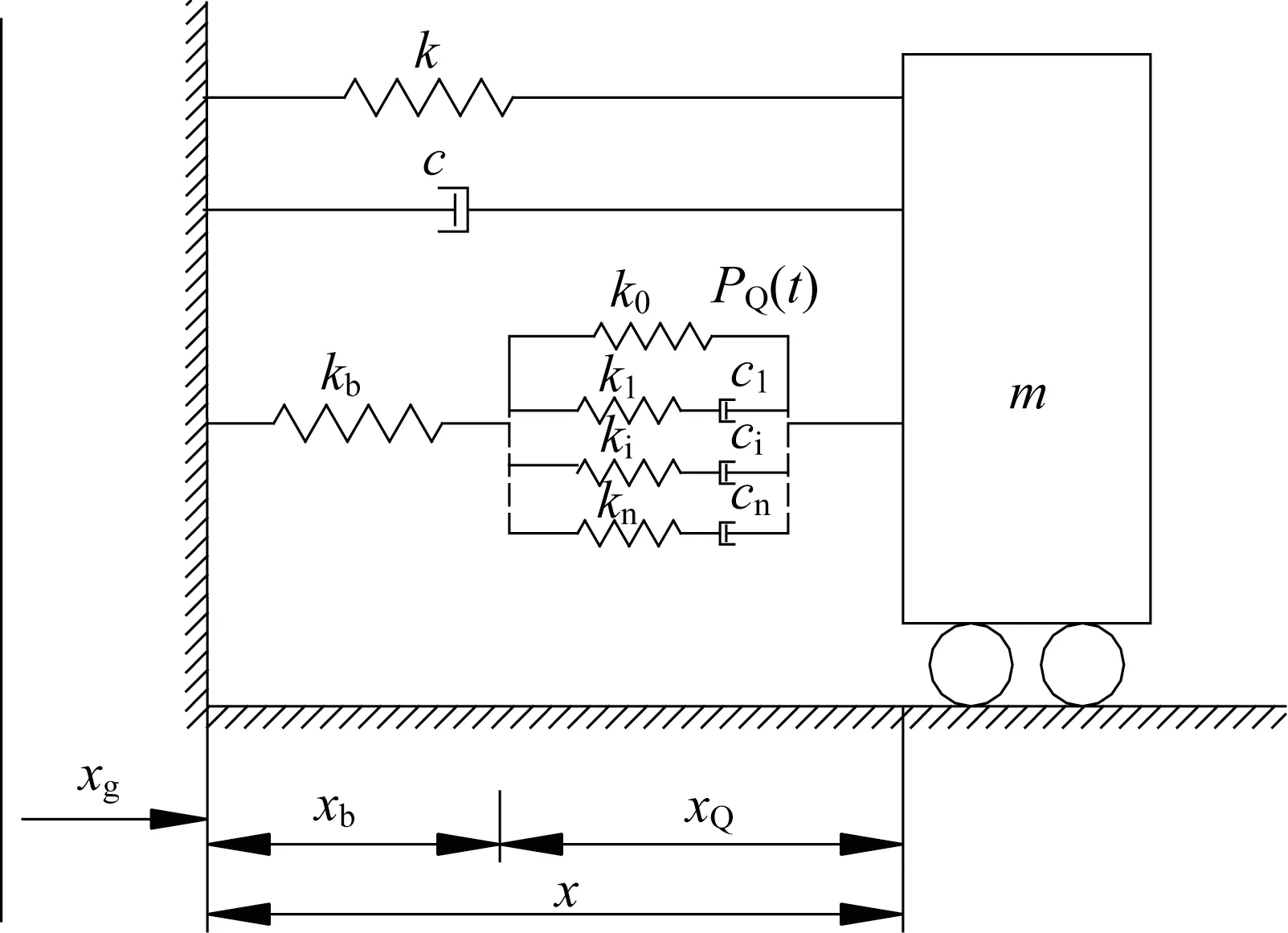
图3 结构模型Fig.3 Model of structure

将式（5）代入式（6），同时考虑式（1）、式（7）和式（6），可以写为

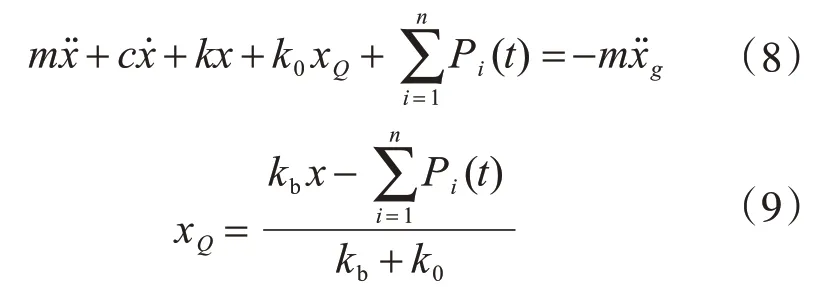
将式（9）分别代入式（8）和式（4），最终可得：

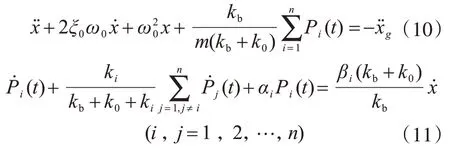
式中：

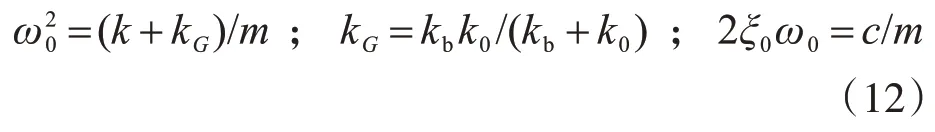
1.4 扩阶方程的建立

令

式（13）、式（10）和式（11）以扩阶的形式表示为

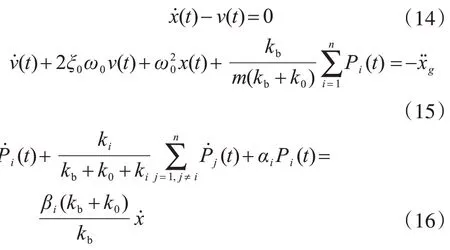
式中：

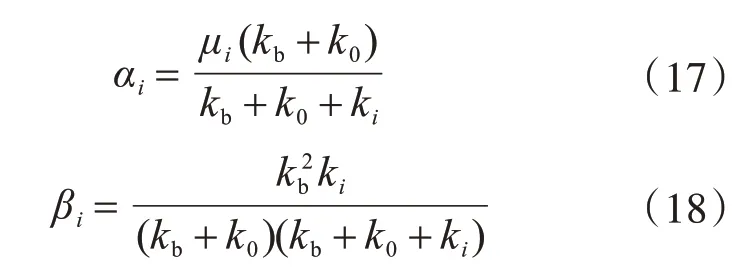
写成矩阵形式为

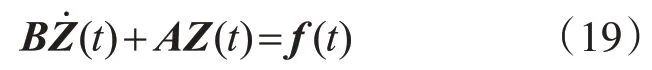
式中：

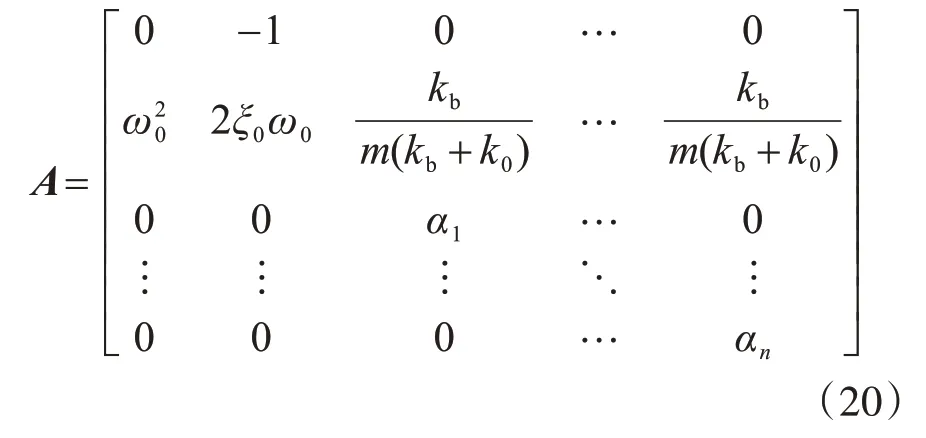
2 非平稳随机地震响应分析的虚拟激励法

2.1 非均匀非平稳地震激励模型

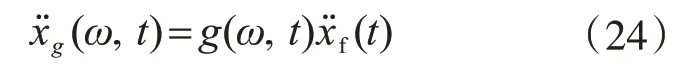
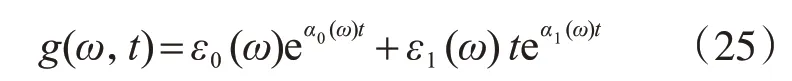
2.2 非均匀非平稳地震响应分析的虚拟激励法

根据虚拟激励法原理［15］将式（1）中替换为可得：

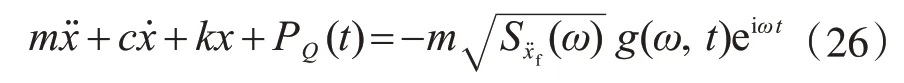
式（19）可改写为

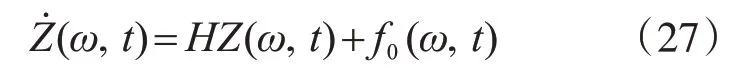
对于多自由度耗能结构体系同样也可化为上式，同样可得多自由度耗能结构体系响应解析解。

式中：

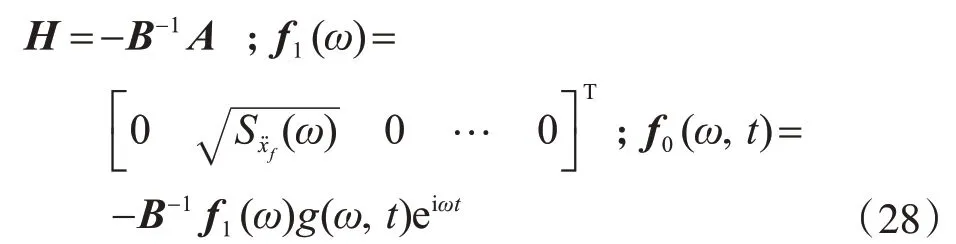
式（27）的通解为齐次解与特解之和，即

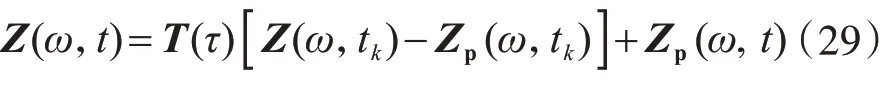
式中：积分步长t ∈[tk，tk+1]，τ=t-tk；关于指数矩阵T(τ)的精细计算，详见文献［19］。

3 非均匀精细积分较一般精确格式

假定在积分步长t ∈[tk，tk+1]内荷载按较一般规律变化，则由式（25）和欧拉公式可得：

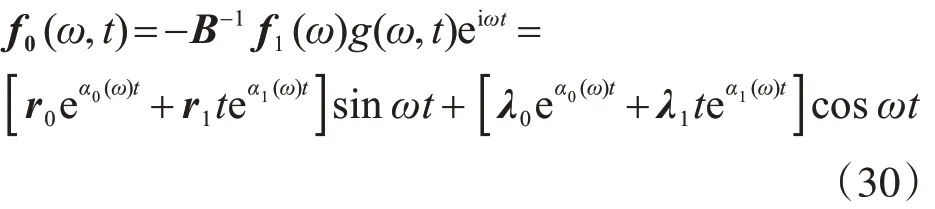
式中：

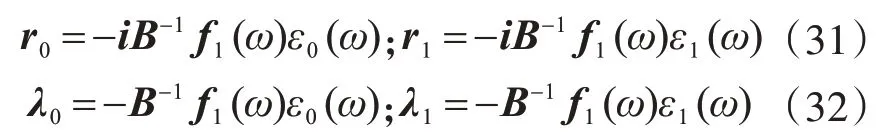
将式（30）代入方程式（27），可得方程的特解Zp(ω，t)为

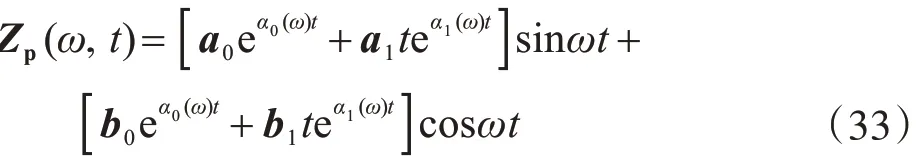
式中：

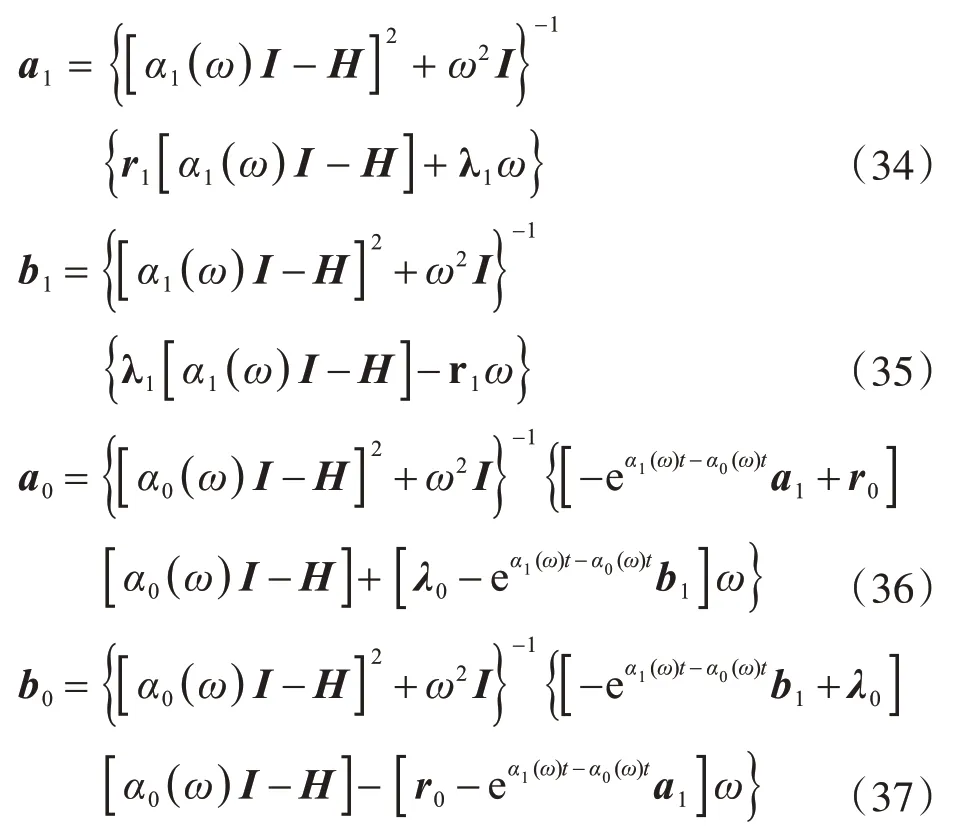
令t=tk+1代入式（29）就得到积分步长终点处的状态：

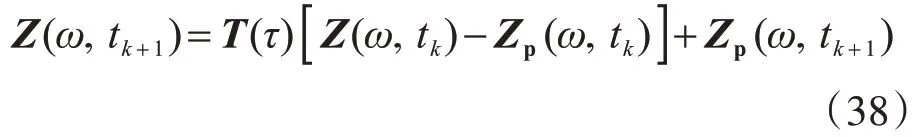
将式（33）代入式（38）即得精细积分较一般精确格式：

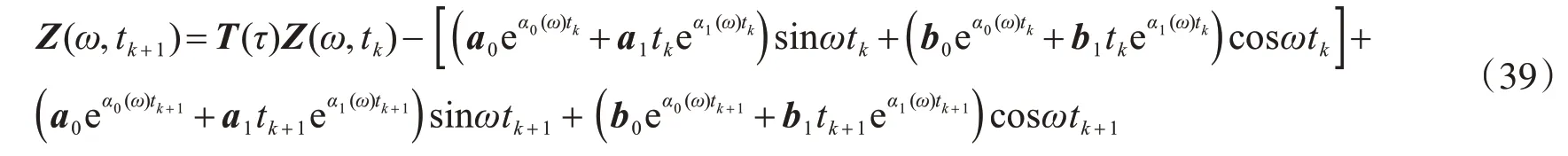
由式（22）和式（39），可以得到地震激励x¨g的响应为z(ω，t)，那么该响应的自谱密度及方差可表示为

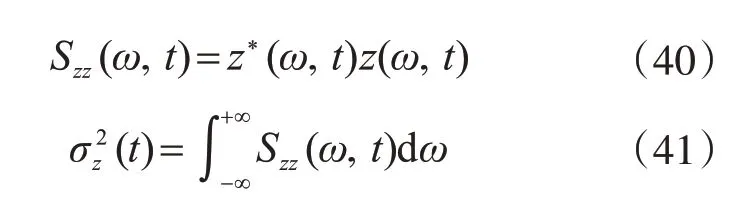
式中，*表示复共轭。

综上步骤，设置支撑的广义Maxwell 阻尼耗能结构的位移、速度，阻尼器受力等非均匀非平稳地震响应均可得到。

4 算 例

如图4 所示，设置支撑的五参数Maxwell 阻尼器单自由度减震系统，其结构的基本参数为：质量m=42 500 kg，刚度k=145.43×105N/m，阻尼比s0分别取0.02、0.04、0.08、0.20。Maxwell阻尼器的基本参数为：平衡刚度k0=0.36×105N/m，支撑刚度kb=1.5k，Maxwell阻尼器两分支单元的刚度和阻尼分别为k1=42.08×105N/m，c1=0.83×105N·s/m；k2=6.87×105N/m，c2=2.15×105N·s/m。

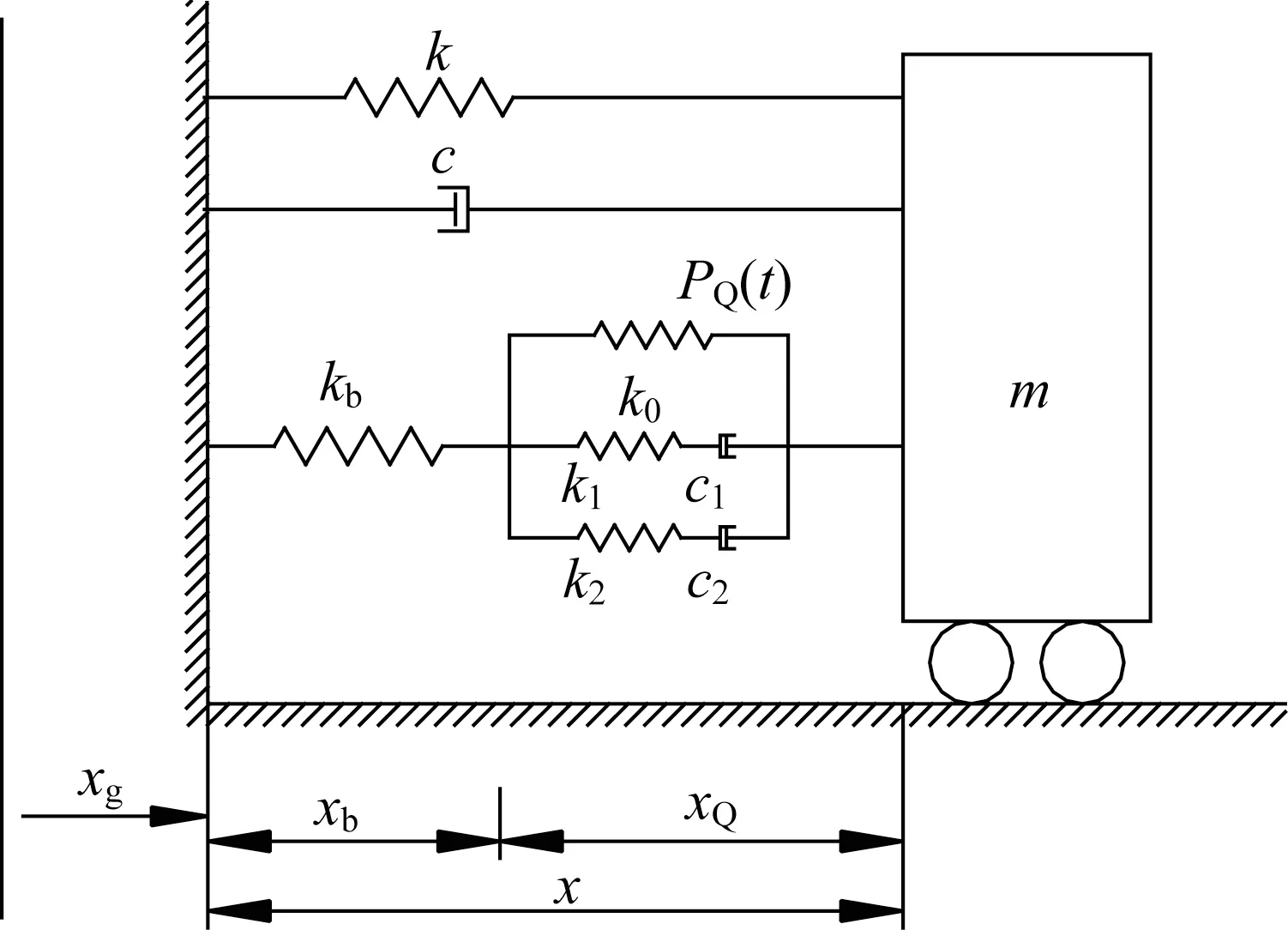
图4 结构计算简图Fig.4 Structure calculation diagram

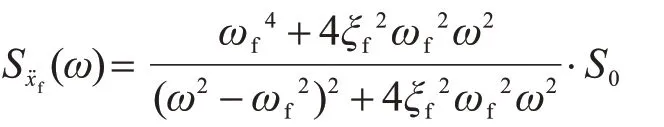
其计算取值为：ωf=19 rad/s，ξf=0.65；S0=0.015 54 m2/s3。

调幅函数分别取为Shinozuka-Sato 型［20］均匀调幅和Spanos-Solomos 型［21］非均匀调幅，计算参数分别取为

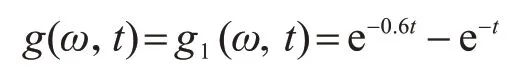
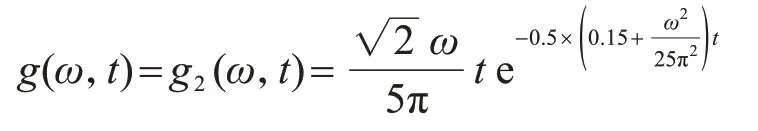
首先，运用本文方法得到Shinozuka-Sato 型均匀调制非平稳地震激励作用下结构响应方差；然后，与精确解［22］进行对比，验证本文方法的正确性与可行性，如图5-图10所示；最后，进一步应用到Spanos-Solomos 型非均匀调制非平稳地震激励作用下结构响应方差，如图11-图13 所示。可以看出：在非平稳激励下，结构的位移、速度和阻尼器受力均具有峰值效应，表现出明显的非平稳随机特性，符合工程实际。

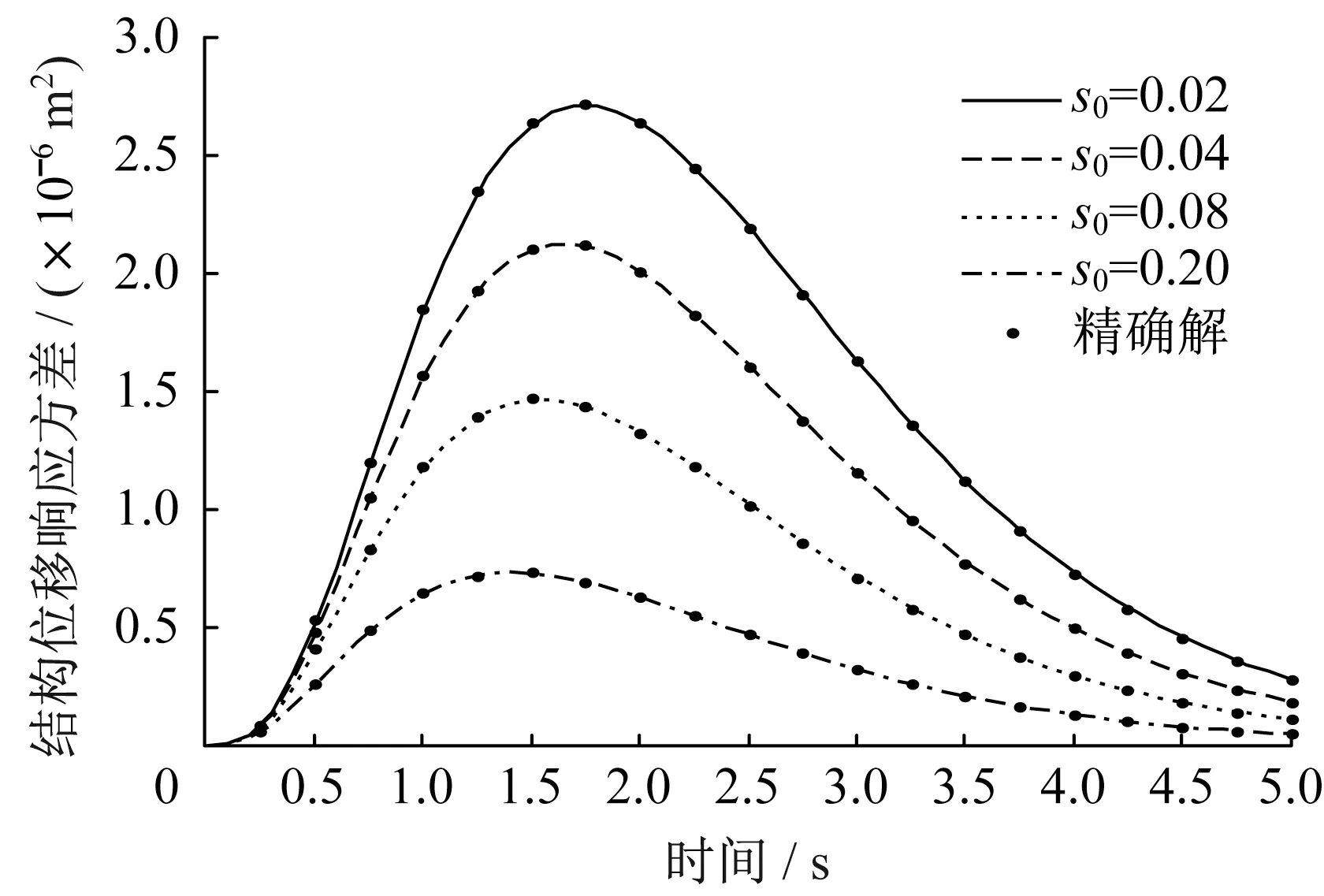
图5 位移响应方差Fig.5 Displacement response variance

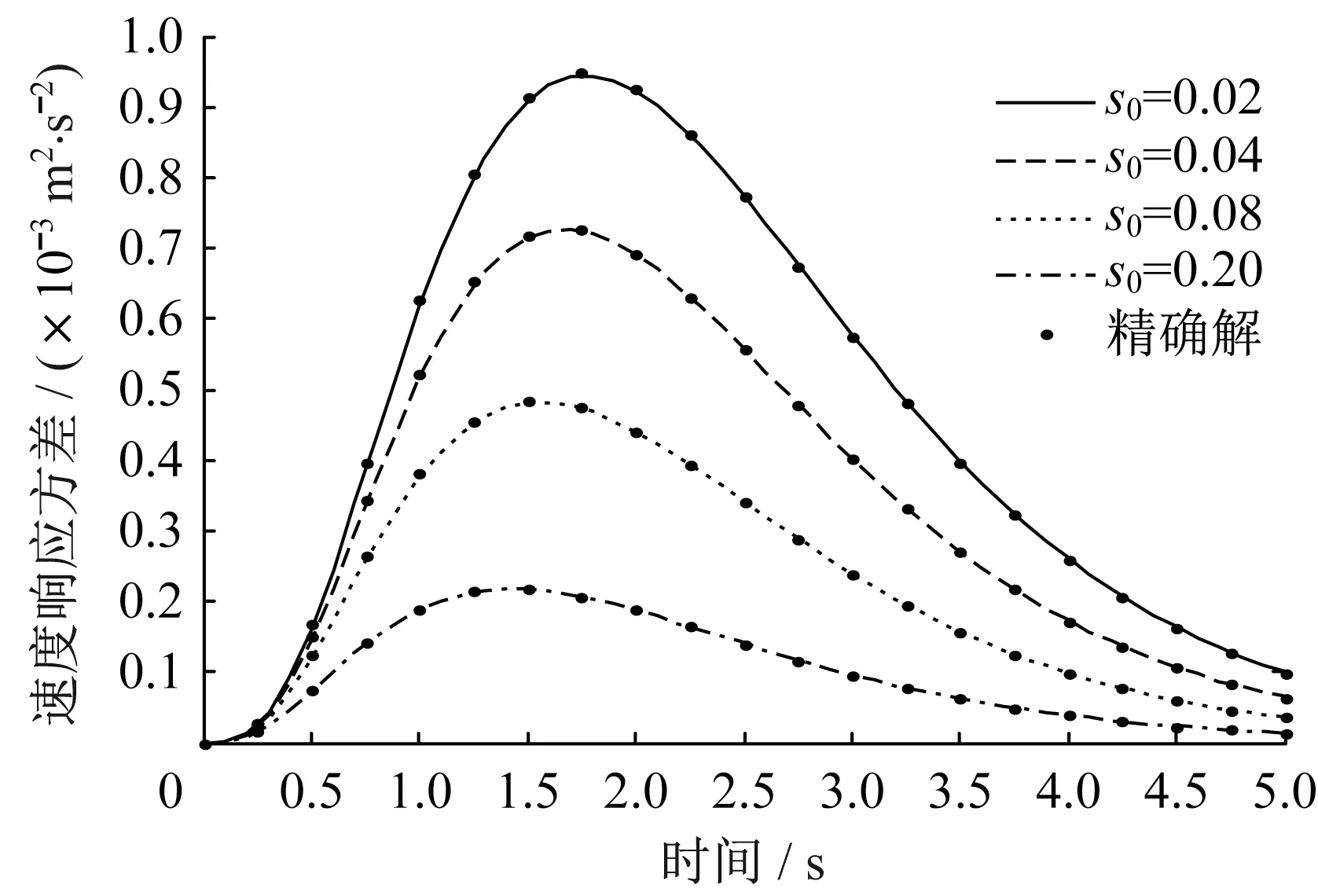
图6 速度响应方差Fig.6 Speed response variance

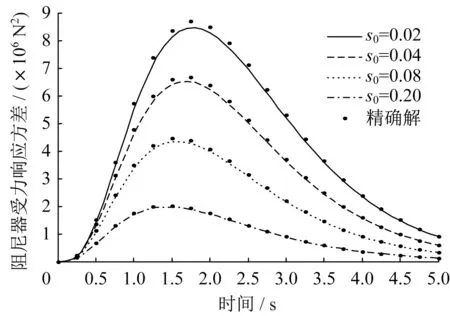
图7 阻尼器受力响应方差Fig.7 Stress response variance of damper

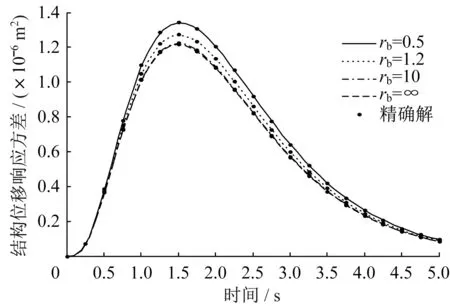
图8 位移响应方差Fig.8 Displacement response variance

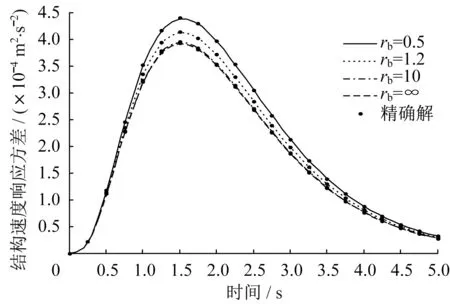
图9 速度响应方差Fig.9 Speed response variance

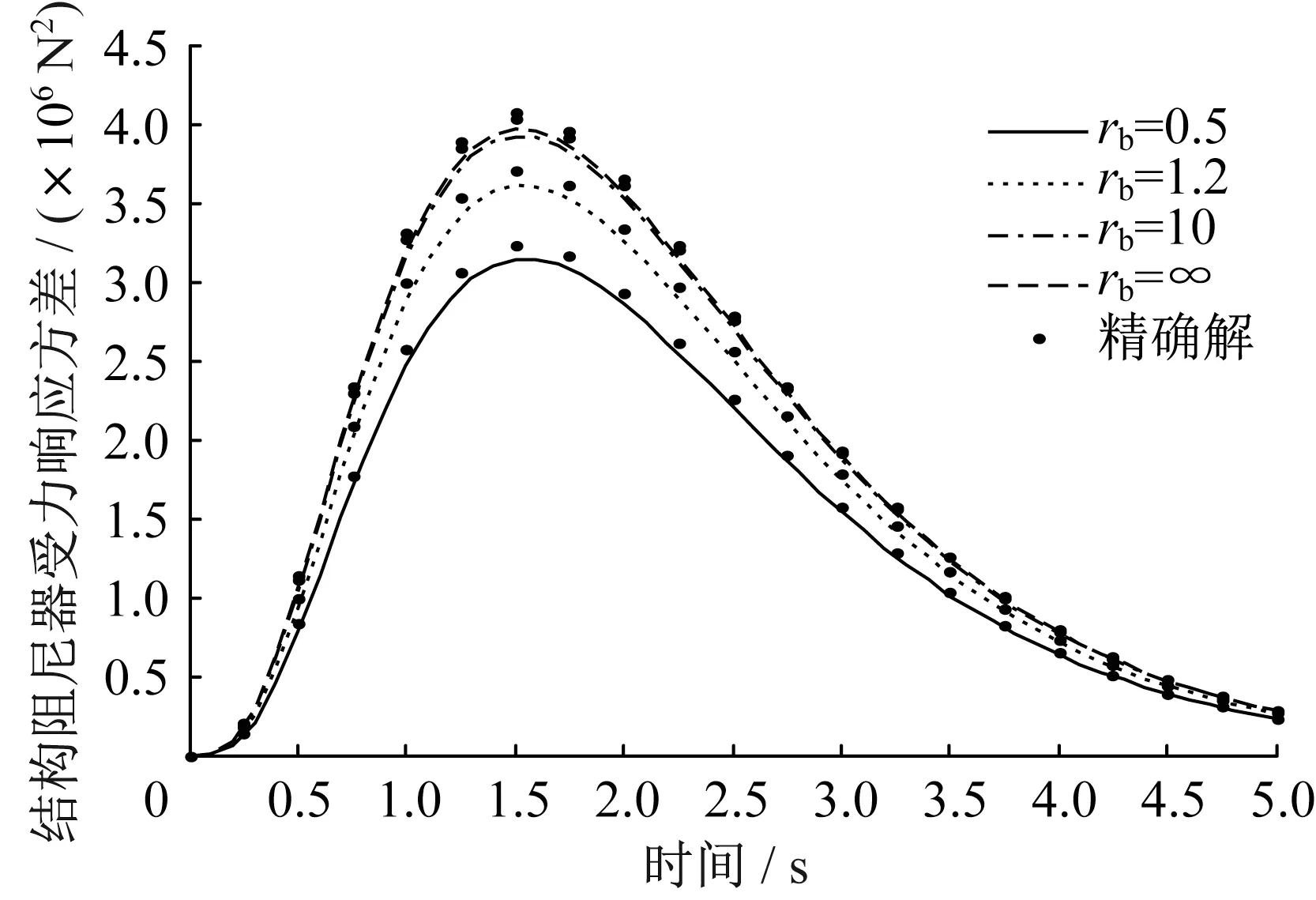
图10 阻尼器受力响应方差Fig.10 Stress response variance of damper

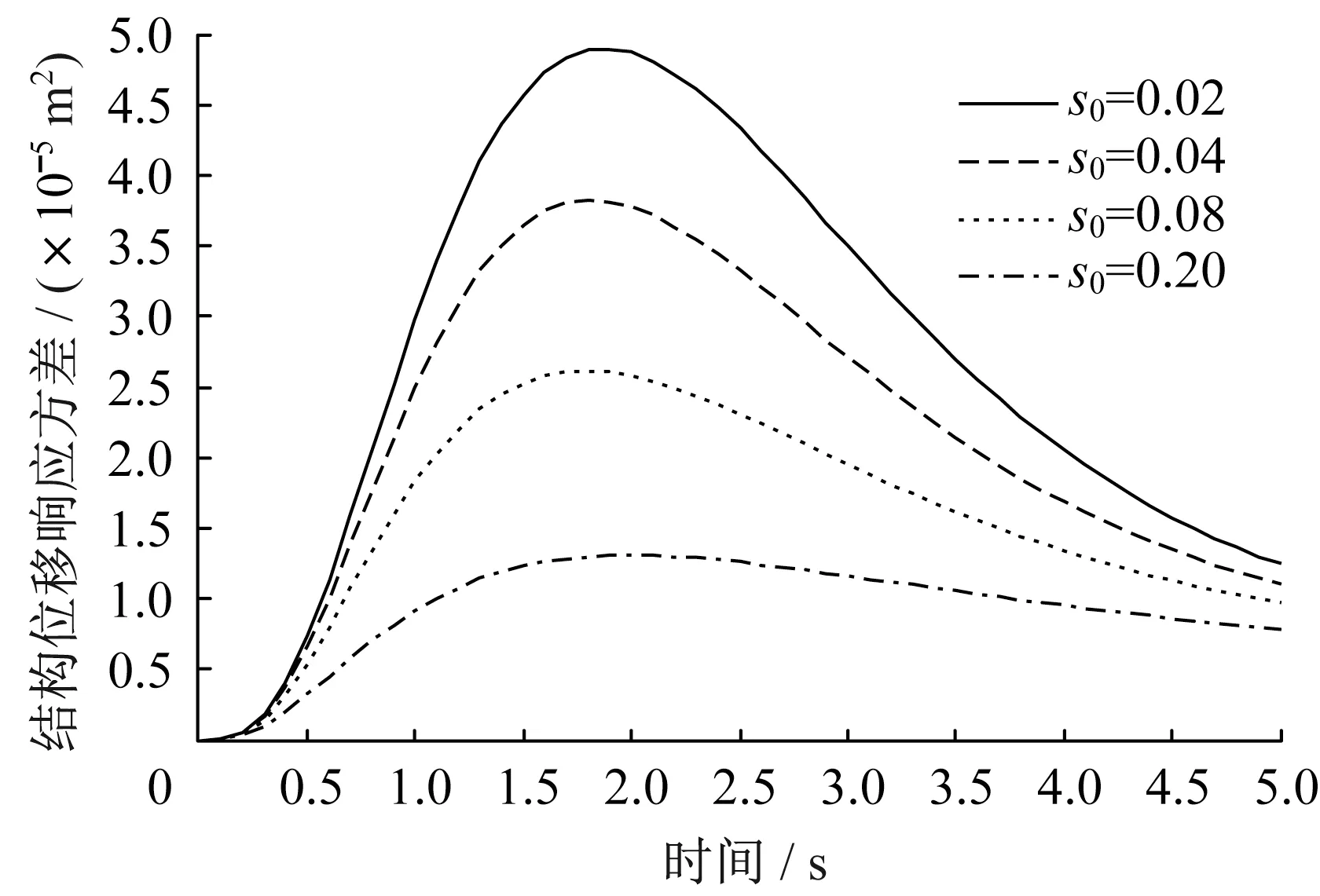
图11 位移响应方差Fig.11 Displacement response variance

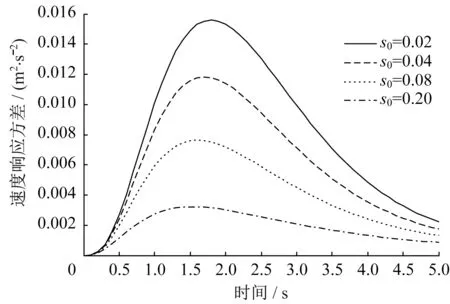
图12 速度响应方差Fig.12 Speed response variance

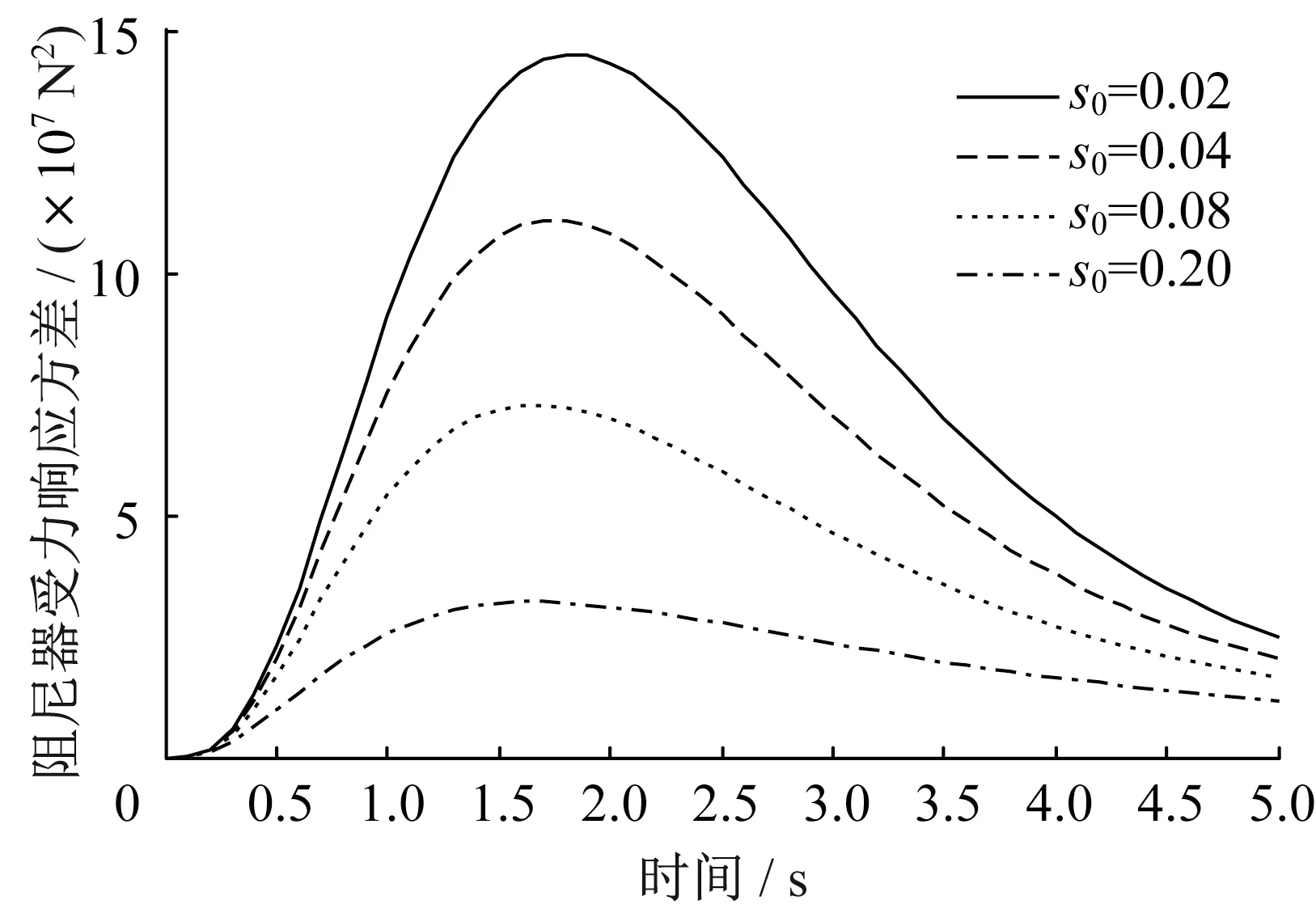
图13 阻尼器受力响应方差Fig.13 Stress response variance of damper

为了研究阻尼比对结构响应的影响，s0分别取0.02、0.04、0.08、0.20。阻尼比对结构响应的影响较大，在两类非平稳激励下，三种响应如图5-图7和11-图13所示。阻尼比越大，响应越早达到峰值，结构的位移、速度和阻尼器受力响应方差均越小。

为了研究支撑刚度对结构响应的影响，结构基本参数不变，而rb分别为0.5、1.2、10、∞，支撑刚度kb=rbk，rb为支撑刚度与结构刚度的比值，阻尼比取s0=0.1，在两类非平稳激励下，三种响应如图8-图10 和14-图16 所示。支撑刚度对结构响应影响较大，响应峰值发生时间不随支撑刚度变化而变化，支撑刚度越大，结构的位移、速度响应方差越小，阻尼器受力响应方差越大。

为确保阻尼器取得较好的减震效果，支撑刚度应取kb≥10k，此时可按kb=∞情况下进行近似计算；对于kb较小的情况，不能按kb=∞情况进行近似计算，应按kb的实际刚度进行计算，否则将会导致错误结果。

5 结 论

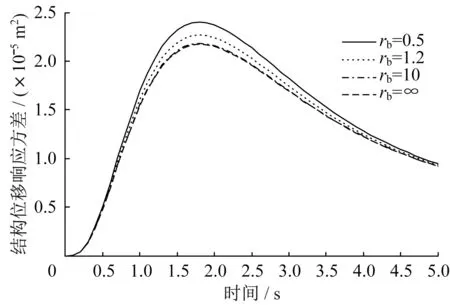
图14 位移响应方差Fig.14 Displacement response variance

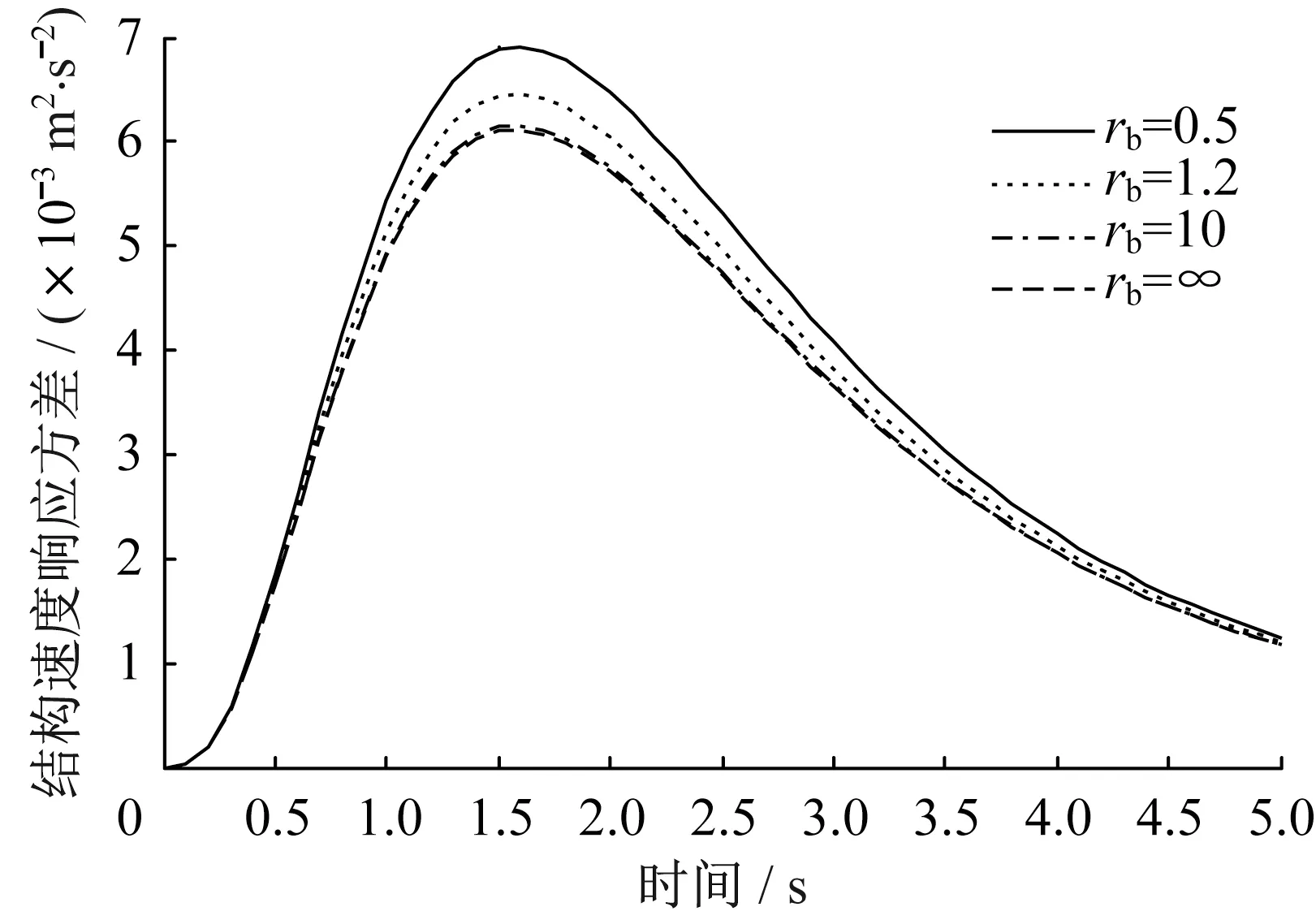
图15 速度响应方差Fig.15 Speed response variance

图16 阻尼器受力响应方差Fig.16 Stress response variance of damper

（1）为建立黏弹性耗能结构及其保护系统的抗震分析与设计方法，本文将虚拟激励法引入黏弹性耗能阻尼系统，获得了非均匀精细积分较一般精确格式，得到了广义Maxwell 阻尼耗能系统的均匀与非均匀非平稳地震响应方差。

（2）通过算例，验证了本文方法的正确性与可行性，该方法适应于设置支撑的广义Maxwell阻尼系统的非均匀非平稳响应分析，可直接应用于黏弹性阻尼耗能系统响应分析。

（3）支撑刚度对黏弹性耗能系统有重要影响，在支撑刚度较耗能系统刚度很大情况下，支撑刚度对耗能系统响应的影响效果不再增加，一般情况下，应考虑有限支撑刚度对耗能系统响应的影响。

（4）尽管本文研究对象是单自由度结构系统，但对于多自由度耗能结构体系也可化为文中式（27）的形式，因此该方法同样可应用于多自由度设置支撑的广义Maxwell 阻尼耗能系统非均匀非平稳地震响应分析，为非均匀非平稳地震激励下结构系统及各减震构件的响应分析和抗震动力可靠度分析提供了参考。