基于Copula函数的松花江流域水文干旱频率分析

廖显薇，高峰，魏婷，宋小燕*，宋松柏

基于Copula函数的松花江流域水文干旱频率分析

廖显薇1，高峰2，魏婷1，宋小燕1*，宋松柏1

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.内蒙古自治区水利科学研究院，呼和浩特 010051）

【】基于Copula函数对松花江流域进行水文干旱频率分析。利用可变阈值法识别日尺度水文干旱事件的历时和烈度，并进行融合处理；选择6种常用的分布函数拟合干旱特征变量，以Kolmogorov-Smirnov 检验法优选单变量边缘分布；从3种Copula函数中优选函数模型，建立了干旱历时和烈度二维联合分布，并计算联合分布概率和重现期，再利用蒙特卡洛方法，讨论基于Copula干旱研究的不确定性。融合标准取c=0.1和c=5，流域干旱历时均值为81~105 d；对数正态分布是大赉站、扶余站和哈尔滨站干旱历时的最优边缘分布，而各个站点干旱烈度最优分布各异；Frank Copula为流域干旱二维联合分布的最优模型，流域大多数干旱的重现期不超过20a；在同现重现期为20 a的条件下，大赉、扶余、哈尔滨和佳木斯4个水文站点的最大可能设计值表现出较大的不确定性。Copula函数能够较好地拟合松花江流域水文干旱特征变量间的联合分布，但需考虑其不确定性影响。

水文干旱；Copula函数；干旱事件融合；松花江流域

0 引言

【研究意义】干旱是一种由水分的收支或供求不平衡而形成的水分短缺现象[1]。随着全球人口增长、气候变暖，各地区对水分的需求量增加，导致干旱频发[2]。东北地区1960—2000年因水旱灾害粮食损失1 498亿kg，直接经济损失达1 585亿元[3]。东北地区是重要的粮食生产基地，对中国的粮食安全起着保障作用。松花江作为黑龙江的支流，在东北地区承担着重要的社会和经济责任。因此，研究松花江流域的干旱问题，对流域的农业生产和生态管理等具有重要意义。

【研究进展】美国气象学会将干旱分为气象干旱、水文干旱、农业干旱及社会经济干旱4个类型[4]。现阶段对松花江流域的干旱研究多集中于气象干旱，而水文干旱研究不足[5]。水文干旱是由河川径流或地下水资源不足导致的结果，相较于气象和农业干旱，水文干旱的发生更加复杂，干旱程度更深、后果更严重[6]。构建多变量联合分布及计算重现期是目前水文干旱研究的重点和难点。Copula函数可克服传统多变量分布函数要求同一类边缘分布函数的限制[7]，单参数Achimedean Copula函数族更因构造简单，相对容易求解，被广泛应用于水文领域[8-10]。【切入点】干旱特征序列样本长度较短，代表性不高，基于样本序列开展的联合分布研究存在显著的不确定性，这对流域水资源合理管理提出了巨大挑战[11]。Copula函数虽已在各个流域的水文干旱频率分析中取得良好的研究成果，但目前关于Copula函数的不确定性研究的报道较少。【拟解决的关键问题】本文选取松花江流域大赉、扶余、哈尔滨和佳木斯4个水文站点1960—2015年的日平均流量，采用可变阈值法识别松花江流域日尺度干旱，通过敏感性测试，确定符合流域水文特性的干旱事件融合标准，再选取常用的伽马、威布尔、对数正态等6种概率分布函数拟合优选干旱特征变量的边缘分布，在此基础上利用Copula函数构建二维干旱变量的联合分布函数并计算重现期，对计算结果进行不确定性探讨。

1 材料与方法

1.1 研究区概况

松花江流域位于中国东北部，有南北两源，北源为嫩江，南源为第二松花江，流域面积为55.68万km²，年径流量为762亿m³。流域地处北温带季风气候区，大陆性气候特点非常明显，冬季寒冷漫长，夏季炎热多雨，春季干燥多风，秋季很短，年内温差较大，多年平均气温在3～5 ℃之间。流域多年平均降水量一般在500 mm左右，汛期6—9月的降水量占全年60%～80%，冬季12—次年2月的降水量仅为全年的5%左右。由于松花江流域主要以大气降水补给为主、融雪补给为辅，因此径流量的年内分配也具有明显的季节特征。

本文选取研究区内大赉站（嫩江汇入松花江干流控制站）、扶余站（第二松花江汇入松花江干流控制站）、哈尔滨站（松花江干流中游控制站）和佳木斯站（松花江干流下游控制站）4个水文站点1960—2015年日平均流量。

1.2 研究方法

1.2.1 基于可变阈值法识别干旱历时和烈度

以4个水文站点的日平均流量数据为基础，使用基于30 d滑动窗口流量—持续时间曲线第80个百分点的可变阈值提取干旱事件的历时和烈度[12]。这意味着，1年中的每一天都有1个不同的阈值水平，这种方法已被用于季节性显著的集水区[13]。当流量低于阈值时，记为干旱，干旱的时长为干旱历时；低于阈值的总缺水量为干旱烈度。在提取的2个历时较长且烈度较大的相邻水文干旱事件之间，存在某一个日径流量超过设定阈值的过程，该过程历时较短，烈度较小，通常认为其前后2个干旱事件是相互关联的，因此，需要建立1个相邻干旱事件的融合标准。以时间间隔t和间隔时间内超阈径流量i与前一个干旱事件所缺径流量的比值i为判别标准[14]，当相邻干旱事件的t和p都低于临界值c和c时，则有：

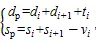
式中：{d，s}和{d1，s1}为2个相邻干旱事件；p和p为相邻干旱事件融合后的干旱历时和烈度。

通过敏感性测试[15]，c取不同值（0、0.05、0.1、0.15、0.2、0.25）；对于日径流过程，c一般取5 d左右（c取2、3、4、5、6 d），对原干旱特征序列（c=0）进行融合，将融合后的历时与烈度均值与原序列均值做比较，得出均值比随c和c的变化曲线。当多条曲线斜率同时变缓时确定c的值，曲线间落差较大时确定c的值，则可得出融合标准。以哈尔滨站为例，其敏感性测试见图1和图2。由图1和图2可以看出，当c=0.1时，5条曲线斜率明显变小，说明干旱历时和烈度的均值变化趋于平缓；当c=6时，干旱均值产生大的跳跃。大赉站、扶余站和佳木斯站均有此情况，因此，本文取c=0.1和c=5两个融合标准。

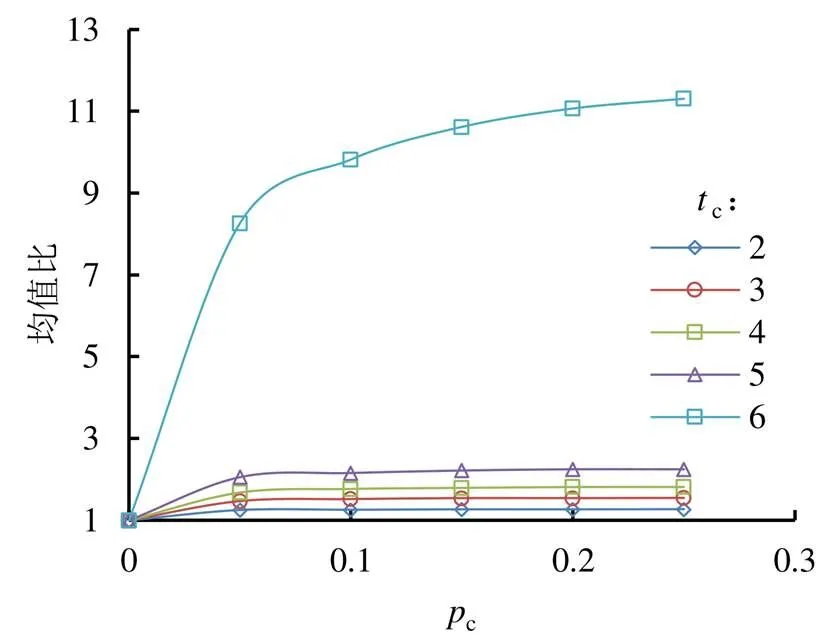
图1 哈尔滨站干旱历时敏感性曲线

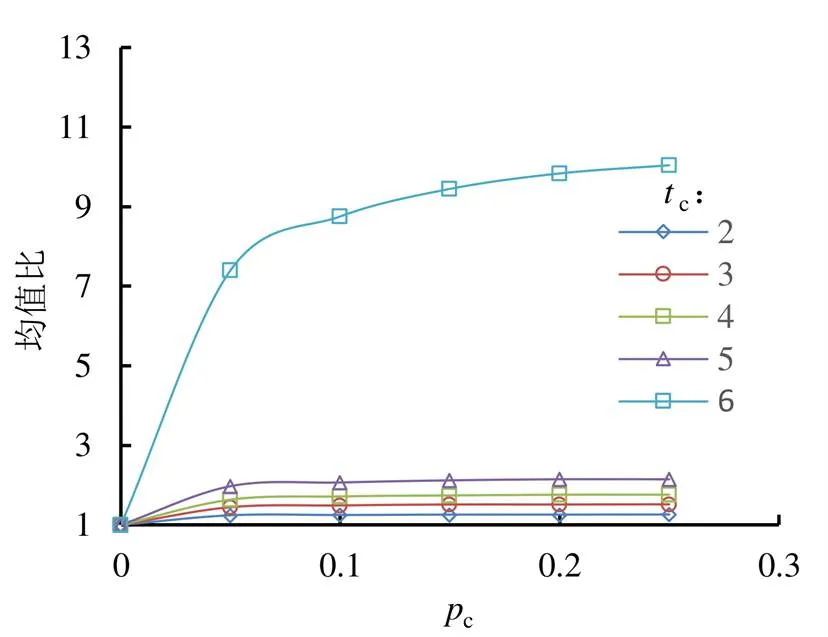
图2 哈尔滨站干旱烈度敏感性曲线

1.2.2 干旱历时和干旱烈度的边缘分布

基于Copula函数的多变量频率分析主要分为单变量频率分析和多变量Copula频率分析2部分[16]，确定干旱特征变量的边缘分布是进行Copula函数选择和参数计算的关键步骤。受气候变化和高强度人类活动影响，水文事件的概率分布函数未知，可通过选取大量候选概率分布函数和拟合优度检验，筛选其中的最优者。本文采用常用的伽马、威布尔、对数正态等6种概率分布函数来拟合干旱历时和烈度，以Kolmogorov-Smirnov检验（K-S）进行拟合优选。本文中边缘分布及联合分布参数均采用最大似然法估计。

1.2.3 基于Copula函数的联合分布

采用Copula函数构建干旱特征变量联合分布之前，需确定干旱特征变量间的相依性。本文采用Kendall、Spearman秩相关系数和Pearson古典相关系数来描述干旱历时和烈度间的相依性。

Copula函数是定义域为[0,1]的均匀分布的多维联合分布函数，它可以将多个随机变量的边缘分布连接起来得到它们的联合分布。

本文选取常用的3种单参数Archimedean Copula函数（Gumbel Copula、Clayton Copula和Frank Copula）构建干旱特征变量的联合分布，其函数和参数取值范围见表1。

表1 Copulas函数及参数取值范围

采用准则和均方根误差检验Copula函数的拟合优度，检验标准值越小，说明函数的拟合程度越好。

1.2.4 干旱历时和干旱烈度的二维联合分布与重现期

1）二维联合概率分布

假定干旱历时的边缘分布函数为D()，干旱烈度的边缘分布函数为S()，干旱历时和烈度的联合分布为：

(,)=(≤,≤)=[D(),S()]=(,)。 （2）

干旱历时和烈度联合超越概率为：

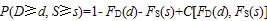
给定≥时，的条件概率：

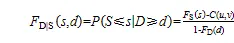
2）重现期

联合重现期：

同现重现期：

式中：为系列长度；为时段内干旱发生次数。

1.2.5 基于蒙特卡洛的联合概率计算不确定性评估

蒙特卡洛方法作为一种常见的分析水文数值模拟不确定性方法，具有实用性广、方法简便的特点，且可将参数的不确定性转化为模拟结果的不确定性[17]。本文利用蒙特卡洛方法，对样本进行多重抽样，计算Copula联合分布下给定重现期的最大可能设计值[18]的置信区间，置信区间能够用来描述水文设计值的不确定性，提供相对可靠的变动范围，可评估样本不确定性对干旱联合分布的影响，详细步骤见文献[19]。

2 结果与分析

2.1 干旱特征变量分析

根据可变阈值法提取干旱特征变量并进行统计可知，1960—2015年，松花江流域水文干旱事件年均发生3.27～4.16次，水文干旱次数发生最多的为中游哈尔滨站，其次为第二松花江扶余站和下游佳木斯站，最少为嫩江大赉站，各水文站点干旱历时和烈度的统计特征（最大值、上四分位数3、均值、中位数、下四分位数1、最小值）见表2。

对干旱历时进行分析可知，大赉站、扶余站、哈尔滨站和佳木斯站历时大于30 d的干旱次数分别占干旱总次数的89%、73%、84%和86%；其中历时大于1 a的干旱分别发生2、4、1和3次；历时最长的干旱分别发生在2012、2014、1965年和1984年；4个水文站的干旱历时主要集中在30～90 d。

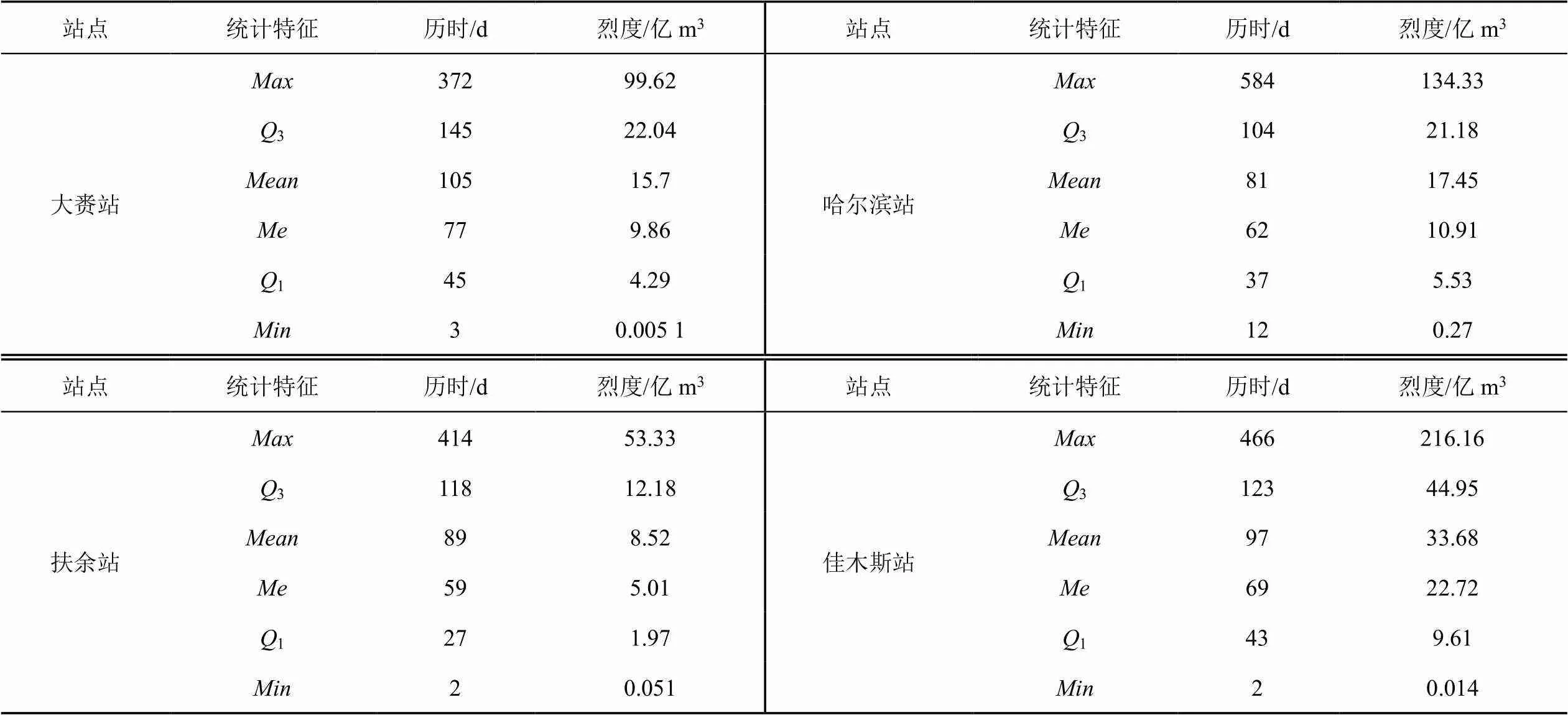
表2 水文干旱历时和烈度统计特征

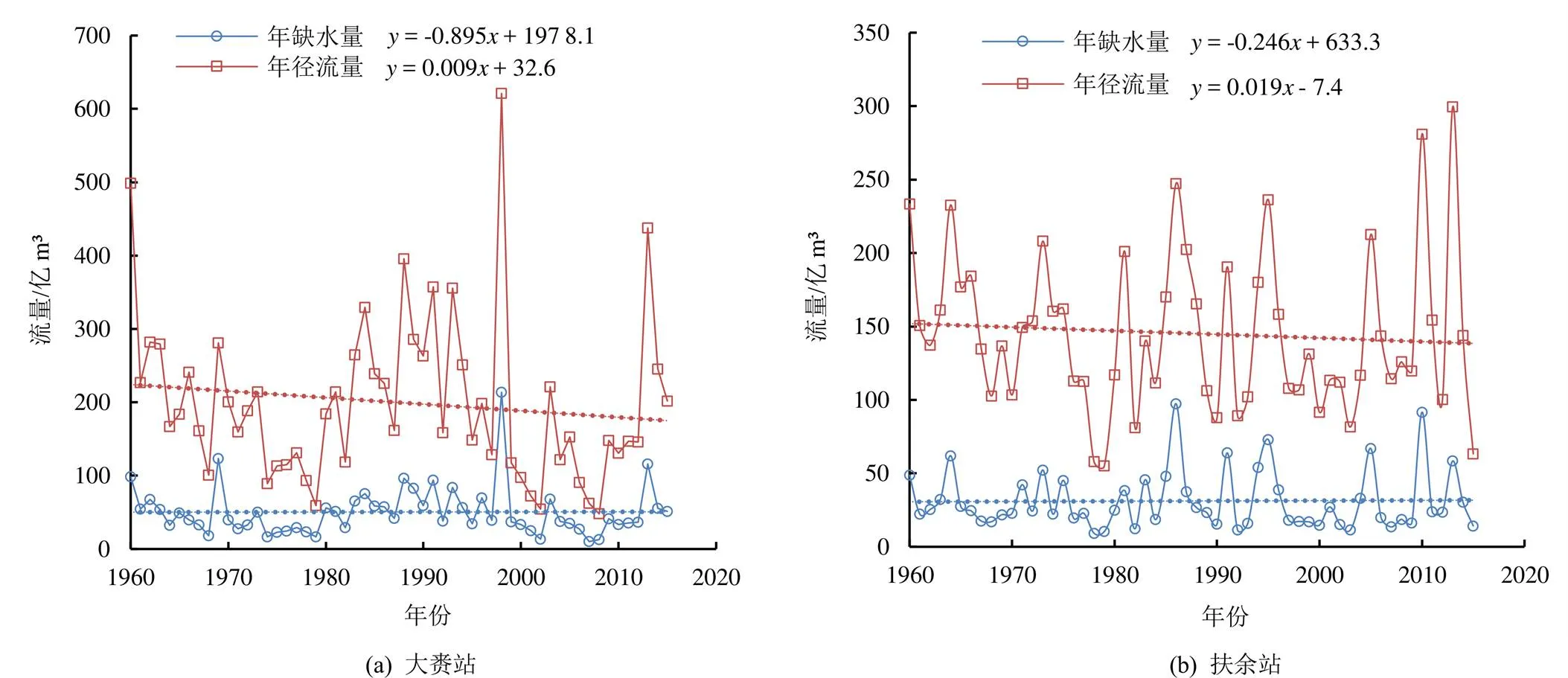
大赉站年平均径流量为199.67亿m3，扶余站年平均径流量为145.22亿m3，哈尔滨站年平均径流量为396.42亿m3，佳木斯站年平均径流量为614.51亿m3。4个站点干旱烈度（缺水量）与年平均径流之比大于10%的干旱发生次数分别为8、4、2和3次，其中烈度最大的干旱分别发生在1998、2005、1998年和1984年，与年平均径流量之比分别为：50%、37%、34%和35%。各个站点的年缺水量与年径流量如图3所示。由图3可知，4个站点的年径流量均呈下降趋势，年缺水量随径流量的增减而波动，说明采用可变阈值法识别的干旱烈度与径流量关联性很强，除佳木斯站有略微下降趋势外，其余3站均有略微上升趋势，大赉站的干旱情况最严重。在干旱事件中，大赉站=28 d，=23.21亿m3、扶余站=25 d，=35.63亿m3、哈尔滨站=26 d，=36.82亿m3和佳木斯站=20 d，=30.25亿m3等干旱事件，虽然干旱历时都小于1个月，但干旱烈度较大，这些“短强干旱”事件大多发生在夏季，其次是春季和秋季，冬季最少。

对干旱历时与烈度序列进行相关性分析，结果见表3。

从表3可以得出，干旱烈度和历时间存在较强的相关性。因此,可以采用Copula函数建立两变量的联合分布模型。

2.2 边缘分布函数的拟合

采用伽马（GAMA）、威布尔（WBL）、对数正态（LOGN）、指数（EXP）、正态（NOR）和广义极值（GEV）等6种概率分布函数来拟合干旱历时和烈度，以K-S方法进行拟合优选，结果见表4。

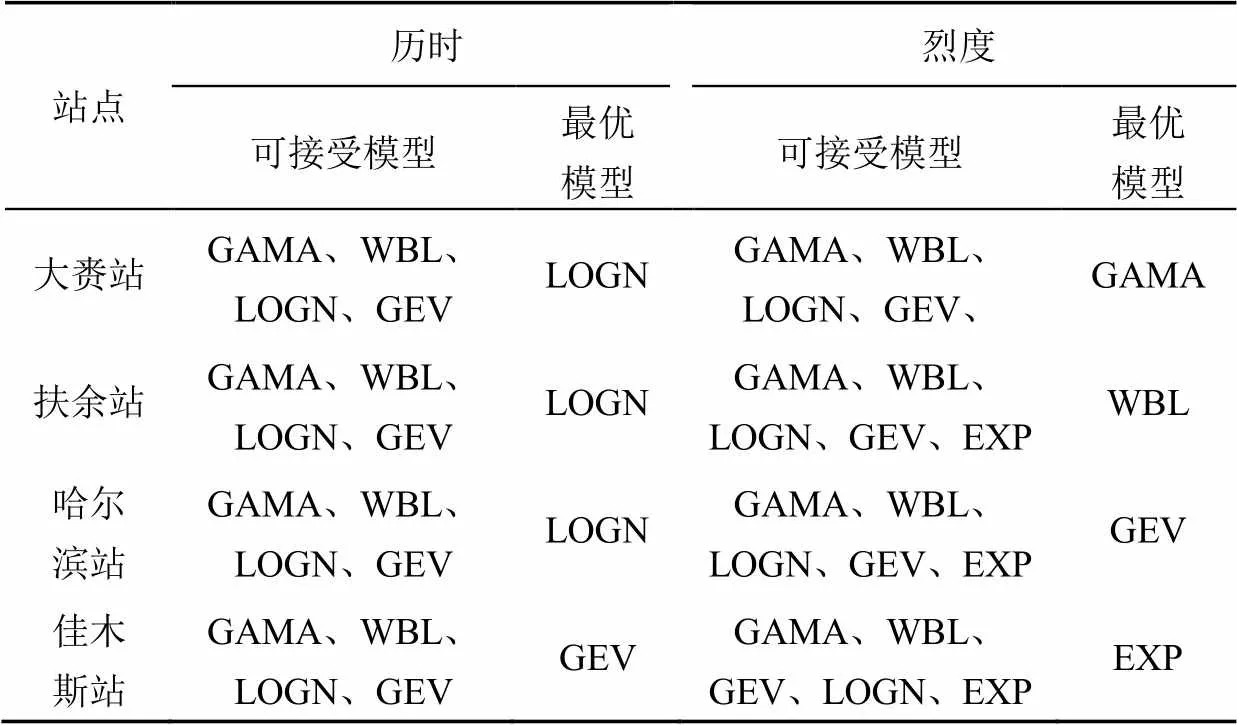
表4 水文干旱特征值边缘分布模型拟合优选

从表4可以得出，LOGN分布为大赉站、扶余站和哈尔滨站干旱历时的最优边缘分布模型，3个站点干旱烈度的最优边缘分布模型分别为GAMA模型、WBL模型和GEV模型。佳木斯站干旱历时和烈度的最优边缘分布模型为GEV模型和EXP模型。

2.3 Copula函数优选

利用3种Copula函数构建干旱历时和烈度的二维联合分布，以和对模型进行拟合优度评价，结果见表5。由表5可知，Frank Copula对大赉站、扶余站、佳木斯站和哈尔滨站的干旱历时与烈度之间的拟合效果最好，优选Frank Copula建立4个站点的二维联合概率及重现期计算。

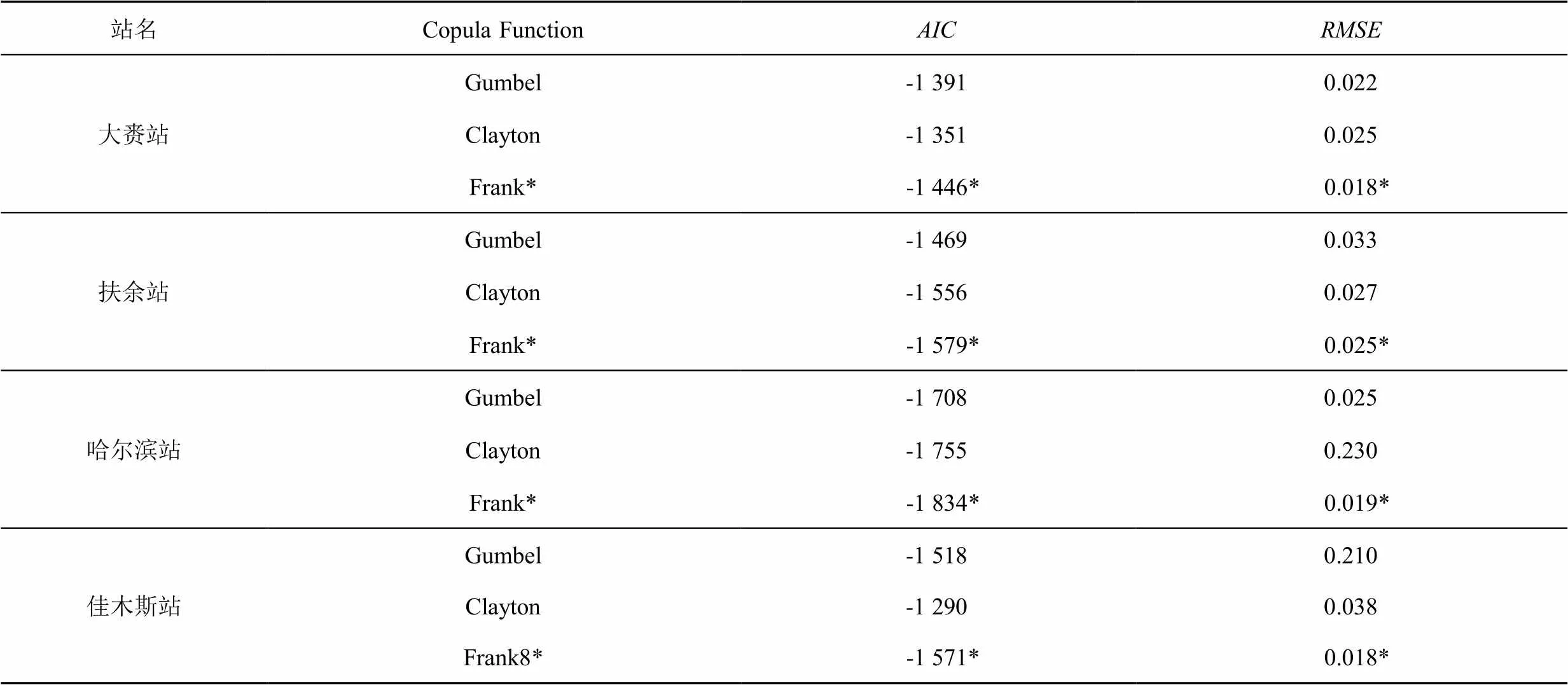
表5 Copulas函数拟合优度评价

注 标*数据对应的和值最小。

2.4 干旱历时和烈度的联合概率

4个水文站点的干旱历时和烈度超越联合概率以及条件概率分布规律相类似，联合概率值随干旱历时和烈度值的减小而呈现增大趋势，表明易发生历时较短且干旱烈度较小的干旱。由图4可以得到，不同历时（≥）下的干旱烈度（≤）所发生的概率。因篇幅限制，图4以佳木斯站为例进行规律阐述。当干旱烈度不大于某一值时，其条件概率随历时的增大而减小，例如当≤50亿m3时，（≥31）>（≥61）>（≥91）。

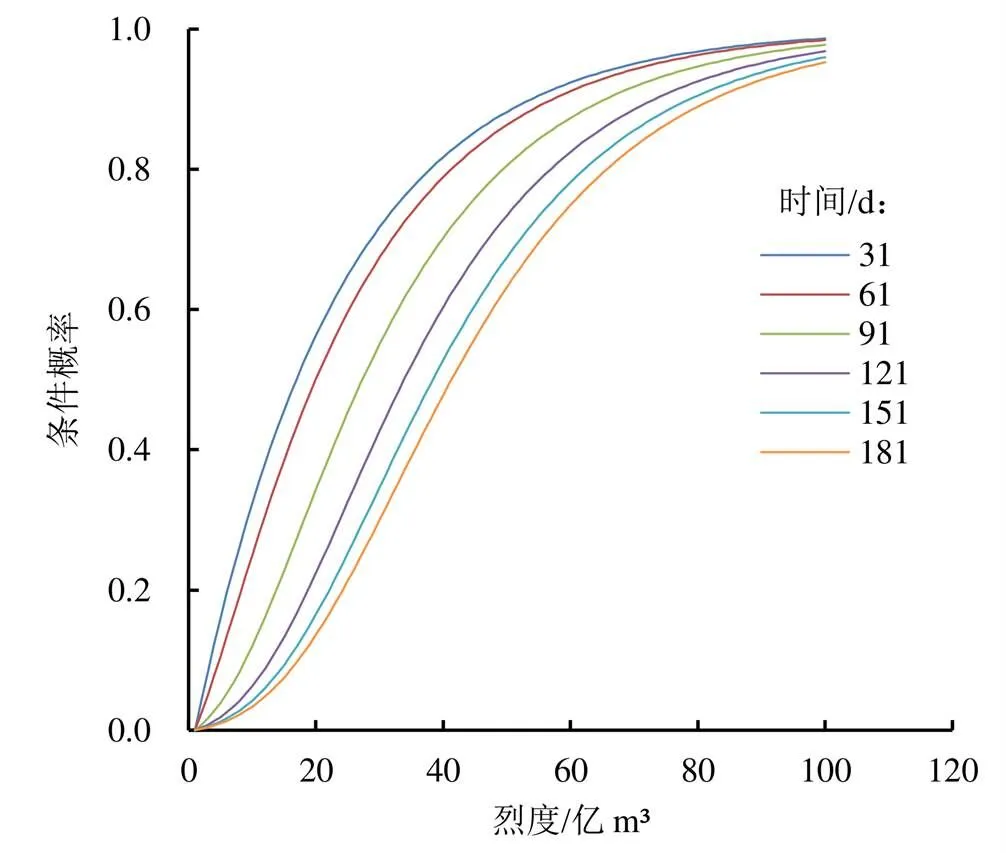
图4 佳木斯站干旱历时与烈度的条件概率

2.5 重现期

利用Frank Copula构建联合分布，再根据式（5）和式（6）计算4个站点的联合重现期和同现重现期，以各个站点干旱历时与烈度的上四分位数统计特征值为界，流域大多数干旱的重现期不超过20 a。大赉站和扶余站的联合重现期比哈尔滨站和佳木斯站小，说明嫩江和第二松花江在遭遇长干旱历时或强干旱烈度的干旱事件的概率要大于松花江干流。而同现重现期则相反，特别是哈尔滨站的同现重现期有内凹的趋势，容易发生历时短且烈度小的干旱。说明流域面积越大，对径流的调节能力越强，对“或”事件的抵御能力越强[20]。

本文重点分析同现重现期为20 a所对应的最大可能设计值，采用蒙特卡洛方法，对干旱特征序列进行多重抽样，获得给定条件下的区间估计，从而讨论其不确定性，联合分布的置信度取95%。分析得出，同现重现期随着干旱历时和烈度的增大而增大。当同现重现期为20a时，所有水文站点的联合设计值二元置信区间面积跨度都较大，哈尔滨站和佳木斯站的置信区间可从5a跨越到50a。将干旱历时与烈度联合设计值二元置信与其单变量边缘分布结合来看，4个水文站点的干旱历时与烈度边缘分布曲线都出现了因水文数据不满足正态分布假设，具有的尖峰、重尾特征，这影响对极端干旱事件的估计，导致干旱历时与烈度联合设计值二元置信区间面积大，增加联合设计值的不确定性。在4个水文站点中，扶余站和大赉站的联合设计值二元置信区间面积跨度没有超过50a重现期，相对松花江干流的哈尔滨站和佳木斯站不确定性较小，原因可能是位于第二松花江干流的控制性工程丰满水库和白山水库与位于嫩江干流的控制性工程尼尔基水库对两个区域的水文干旱有调节作用，可以减少联合设计值的不确定性。

3 讨论

本研究采用可变阈值法，能够适应径流季节性变化，通过敏感性试验，选取的融合标准与涂新军等[21]在东江流域的研究一致，研究方法可靠。松花江流域的水文干旱历时均值3个月，水文干旱有加重趋势，嫩江大赉站的干旱情况最严重，与韩冬梅等[22]的研究结果相符。除此之外，值得注意的是，研究结果中一些“短强干旱”事件具有明显的季节性特征，大多发生在夏季，其次是春季和秋季。这应与松花江流域以降水补给为主、融雪补给为辅的不均匀来水情况有关。夏秋季遇强降雨时会形成洪涝，春季受融雪补给的作用，各河流会形成程度不等的春汛，当短期内发生洪水或丰枯季节交替时，日流量变异大，导致与阈值的差积增大。不仅如此，径流年内分配的不均匀性在区域上也存在差异。相较于第二松花江和松花江干流，嫩江流域的水文站点年内径流分配最不均匀[23]，这可能是导致大赉站干旱情况严重的原因之一。

在获取干旱特征的基础上，本文优选Frank Copula构建联合分布模型并计算松花江流域水文干旱重现期，重点讨论同现重现期为20a的条件下，最大可能设计值的二元置信区间，表现出很强的不确定性，大赉站和扶余站的不确定性较松花江干流小。水文设计值不确定的影响因素主要集中在3个方面[24]：①水文事件本身的不确定性；②线型选择的不确定性；③模型参数估计方法的不确定性。松花江干流有松嫩平原和三江平原，居民数量多，活动范围广，人类活动通过改变大气循环和通过蓄、引、提、调水工程等改变河流蓄存状态和水力联系[25]，加大了水文事件的不确定性；干旱特征边缘分布线型的选取缺乏物理根据，仅仅是一种数值拟合，因此线型选择的偏差，也存在不确定性[26]；分布函数确定情况下，参数估计方法不同，其水文设计值置信区间估计方法不同。李航等[27]研究6种参数估计方法发现，优化适线法和线性矩法在水文频率分析中较极大似然法取得的拟合效果更为理想。综上所述，联合分布不确定性是多因素所致的客观现象，今后的研究可通过对初始条件的确定、模型的优化等途径，使输出结果更加精确[28]。

已有很多研究将Copula函数用于各个流域的水文干旱频率分析计算中，在前人研究的基础上，本文讨论了基于Copula函数联合分布的不确定性，对流域管理决策的制定有非常重要的意义。本文也存在一些不足，如干旱特征除历时和烈度外，还有峰值和面积等特征，二维联合分布仍不能满足实际需要；其次，在干旱年际对比上，可变阈值法表现出一定的不足，它展现不出丰枯年份的差异，且未将干旱烈度标准化，无法直接体现干旱严重的空间异质性。另外，本文仅对水文干旱频率的不确定性进行了研究，如何解决不确定性产生的影响等问题，需在今后的研究中进行更深入的探讨。目前Copula函数已有上百种，如何将其成熟的用于干旱研究仍是未来一段时间内的研究难点。

4 结论

1）本文运用可变阈值法对松花江流域4个水文站的日径流量进行干旱识别，取c=5和c=0.1为融合标准，得到松花江流域水文干旱历时均值为81～105 d，烈度均值为8.52亿～33.68亿m3，且存在历时小于1个月，烈度较大的干旱事件。

2）对数正态、伽马、威布尔和广义极值等分布能较好地拟合干旱历时和烈度的边缘分布；Frank Copula对大赉站、扶余站、哈尔滨站和佳木斯站的干旱历时与烈度之间的拟合效果最好。

3）超越联合概率值随干旱历时和烈度的减小而呈增大趋势，而重现期则相反。松花江流域所发生的干旱大多数重现期不超过20a。在同现重现期为20a的条件下，4个站点的最大可能设计值置信区间较大，最大跨越5~50a，不利于流域工程设计值的确定。

[1] 洪兴骏, 郭生练, 王乐, 等. 基于最大熵原理的水文干旱指标计算方法研究[J]. 南水北调与水利科技, 2018, 16(2): 93-99.

HONG Xingjun, GUO Shenglian, WANG Le, et al. Hydrological drought index calculation using Principle of Maximum Entropy[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(2): 93-99.

[2] 赵福年, 王润元, 王莺, 等. 干旱过程､时空尺度及干旱指数构建机制的探讨[J]. 灾害学, 2018, 33(4): 32-39.

ZHAO Funian, WANG Runyuan, WANG Ying, et al. Discussion of process, temporal and spatial for drought and establishment of drought indexs[J]. Journal of Catastrophology, 2018, 33(4): 32-39.

[3] 水利部松辽水利委员会. 东北区水旱灾害集[M]. 长春: 吉林出版社, 2003: 25-81.

Songliao Water Resources Commission, Ministry of Water Resources. Flood and drought disasters in Northeast China[M]. Changchun: Jilin Press, 2003: 25-81.

[4] HEIM J, RICHARD R. A review of twentieth-century drought Indices used in the united states[J]. Bulletin of the American Meteorological Society, 2002, 83(8): 1 149-1 165.

[5] 吴燕锋, 章光新. 松花江区气象水文干旱演变特征[J]. 地理科学, 2018, 38(10): 1 731-1 739.

WU Yanfeng, ZHANG Guangxin. Spatio-temporal patterns of meteorological and hydrological drought in the Songhua River Area from 1961 to 2010[J]. Scientia Geographica Sinica, 2018, 38(10): 1 731-1 739.

[6] 董前进, 谢平. 水文干旱研究进展[J]. 水文, 2014, 34(4): 1-7.

DONG Qianjin, XIE Ping. Advances in hydrological research[J]. Hydrology, 2014, 34(4): 1-7.

[7] 宋松柏, 王小军. 基于Copula函数的水文随机变量和概率分布计算[J]. 水利学报, 2018, 49(6): 687-693.

SONG Songbai, WANG Xiaojun. Probability distribution calculation of the sum of hydrological random variables based on Copula function approach[J]. Journal of Hydraulic Engineering, 2018, 49(6): 687-693.

[8] 袁超, 宋松柏. 基于Copula函数的水文干旱联合概率分布研究[J]. 水利与建筑工程学报, 2016, 14(6): 50-53.

YUAN Chao, SONG Songbai. The bivariate hydrologic drought distribution based on copula function[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(6): 50-53.

[9] 张迎, 黄生志, 黄强, 等. 基于Copula函数的新型综合干旱指数构建与应用[J]. 水利学报, 2018, 49(6): 703-714.

ZHANG Ying, HUANG Shengzhi, HUANG Qiang, et al. Construction and application of a new comprehensive drought index based on Copula function[J]. Journal of Hydraulic Engineering, 2018, 49(6): 703-714.

[10] 顾世祥, 赵众, 陈晶, 等. 基于高维Copula函数的逐日潜在蒸散量及气象干旱预测[J]. 农业工程学报, 2020, 36(9): 143-151.

GU Shixiang, ZHAO Zhong, CHEN Jing, et al. Daily reference evapotranspiration and meteorological drought forecast using high-dimensional Copula joint distribution model[J]. Chinese Society of Agricultural Engineering, 2020, 36(9): 143-151.

[11] ZHANG Q, XIAO M Z, SINGH V P. Uncertainty evaluation of copula analysis of hydrological droughts in the East River basin, China[J]. Global and Planetary Change, 2015, 129(6): 1-9.

[12] BEYENE B, VAN LOON A F, VAN LANEN H A J, et al. Investigation of variable threshold level approaches for hydrological drought identification[J]. Journal of Hydrology, 2015, 512(11): 421-434.

[13] VAN LOON A F, LAAHA G. Hydrological drought severity explained by climate and catchment characteristics[J]. Journal of Hydrology, 2015, 526(12): 3-14.

[14] MADSEN H, ROSBJERG D. On the modelling of extreme droughts[J]. Water Resources Systems, 1995, 231(6): 377-385.

[15] LENA M T, HENRIK M, BENTE C. On the definition and modelling of streamflow drought duration and deficit volume[J]. Hydrological Sciences Journal, 1997, 42(1): 15-33.

[16] 徐翔宇, 许凯, 杨大文, 等. 多变量干旱事件识别与频率计算方法[J]. 水科学进展, 2019, 30(3): 373-381.

XU Xiangyu, XU Kai, YANG Dawen, et al. Drought identification and drought frequency analysis based on multiple variables[J]. Advances in Water Science, 2019, 30(3): 373-381.

[17] 苗添升, 卢文喜, 欧阳琦, 等. 地下水数值模拟的不确定性分析在水质预测中的应用[J]. 水电能源科学, 2016, 34(8): 20-23, 44.

MIAO Tiansheng, LU Wenxi, OUYANG Qi, et al. Application of Uncertainty Analysis of Groundwater Numerical Simulation in Water Quality Prediction[J]. Water Resources and Power, 2016, 34(8): 20-23, 44.

[18] SALVADORI G, DE MICHELE C, DURANTE F. On the return period and design in a multivariate framework[J]. Hydrology and Earth System Sciences, 2011, 15(11): 3 293-3 305.

[19] 马川惠, 黄强, 郭爱军. 泾河流域水沙联合分布特征分析及其不确定性评估[J]. 水利学报, 2019, 50(2): 273-282.

MA Chuanhui, HUANG Qiang, GUO Aijun. Characteristic analysis and uncertainty assessment of joint distribution of flow and sand in Jinghe River basin[J]. Journal of Hydraulic Engineering, 2019, 50(2): 273-282.

[20] 姚蕊, 孙鹏, 张强, 等. 基于Copula淮河流域水文干旱频率分析及影响研究[J]. 北京师范大学学报(自然科学版), 2019, 55(6): 755-763.

YAO Rui, SUN Peng, ZHANG Qiang, et al. Hydrological drought frequency based on Copulas in Huai River Basin[J]. Journal of Beijing Normal University Natural Sciences, 2019, 55(6): 755-763.

[21] 涂新军, 陈晓宏, 赵勇, 等. 变化环境下东江流域水文干旱特征及缺水响应[J]. 水科学进展, 2016, 27(6): 810-821.

TU Xinjun, CHEN Xiaohong, ZHAO Yong, et al. Responses of hydrological drought properties and water shortage under changing environments in Dongjiang River basin[J]. Advances in Water Science, 2016, 27(6): 810-821.

[22] 韩冬梅, 杨贵羽, 严登华, 等. 近50年东北地区旱涝时空特征分析[J]. 水电能源科学, 2014, 32(6): 5-8.

HAN Dongmei, YANG Guiyu, YAN Denghua, et al. Spatial-temporal feature analysis of drought and flood in Northeast China in recent 50 years[J]. Water Water Resources and Power, 2014, 32(6): 5-8.

[23] 李峰平. 变化环境下松花江流域水文与水资源响应研究[D]. 长春: 中国科学院研究生院(东北地理与农业生态研究所), 2015.

LI Fengping. Study on water cycle and water resources in Songhua River Basin under the Changing Environment[D]. Changchun: Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, 2015.

[24] 雷冠军, 王文川, 殷峻暹, 等. P-Ⅲ型曲线参数估计方法研究综述[J].人民黄河, 2017, 39(10): 1-7.

LEI Guanjun, WANG Wenchuan, YIN Junxian, et al. Review on study of parameter estimation method on P-Ⅲcurve[J]. Yellow River, 2017, 39(10): 1-7.

[25] 王文, 王靖淑, 陶奕源, 等. 人类活动对水文干旱形成与发展的影响研究进展[J]. 水文, 2020, 40(3): 1-8.

WANG Wen, WANG Jingshu, TAO Yiyuan, et al. Review of human impacts on formation and development of hydrologic drought[J]. Journal of China Hydrology, 2020, 40(3): 1-8.

[26] 刘攀, 郭生练, 田向荣, 等. 基于贝叶斯理论的水文频率线型选择与综合[J]. 武汉大学学报(工学版), 2005, 38(5): 38-42.

LIU Pan, Guo Shenglian, Tian Xiangrong, et al. Selecting and averaging of flood frequency models based on Bayesian theory[J]. Engineering Journal of Wuhan University, 2005, 38(5): 38-42.

[27] 李航, 宋松柏, 石继海. 指数Gamma分布参数估计方法对比研究[J]. 水力发电学报, 2019, 38(4): 96-107.

LI Hang, SONG Songbai, SHI Jihai. Comparison of parameter estimation methods for exponential Gamma distribution[J]. Jourmal of Hydroelectric Engineering, 2019, 38(4): 96-107.

[28] 强安丰, 汪妮, 莫淑红, 等. 气候变化对水文水资源影响评价的不确定研究进展[J].水资源研究, 2020, 9(2): 169-178.

QIANG Anfeng, WANG Ni, MO Shuhong, et al. Review for impact assessment of climate change on hydrology and water resources in uncertainties research[J]. Journal of Water Resources Research, 2020, 9(2): 169-178.

Using Copula Method to Analyze Drought Frequency in Songhua River Basin

LIAO Xianwei1, GAO Feng2, WEI Ting1, SONG Xiaoyan1*, SONG Songbai1

(1. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China 2.Inner Mongolia Water Conservancy Research Institute, Hohhot 010051, China)

Drought could significantly impact hydrological processes and water resources, and understanding frequency and uncertainty of drought occurrence is hence imperative to water resources planning. The copula method has emerged as an improved multivariate analysis over the univariate analysis for quantitative analysis of drought.【】This paper is to present the results of the frequency and severity of droughts in Songhua river basin calculated using the copula multivariate method.【】The analysis was based on archived data, and duration and severity of the pooled daily drought events were identified using the variable threshold level method. The drought index variables were fitted by six common distribution functions respectively, and they were then evaluated using the Kolmogorov Smirnov test method. Optimal model selected from three Copula functions was used toestablish a two-dimensional joint distribution for the drought index variables, from which we calculated the joint distribution probability as well as the return period.The uncertainty of the drought was analyzed using the Monte Carlo method.【】With the pooling criteria set to bec=0.1 andc=5, the average drought duration was 81~105 days in the basin. The lognormal distribution can adequately describe the marginal distribution of the drought duration in Dalai, Fuyu and Harbin stations in the basin, despite the differences in optimal distribution of the drought severity between them. The Frank copula was the best model for the two-dimensional joint distribution of the drought, and the return periods of the droughts were less than 20 years. When the return period was 20 years, the maximum design values for Dalai, Fuyu, Harbin and Jiamusi hydrological stations were most uncertain.【】The copula multivariate model can adequately describe the joint distribution of the drought index variables in Songhua river basin, and its application should consider drought uncertainty.

hydrologicaldrought; Copula function; pooling of drought events; Songhua river basin

P333

A

10.13522/j.cnki.ggps.2020330

1672 - 3317（2021）03 - 0134 - 08

廖显薇,高峰, 魏婷, 等. 基于Copula函数的松花江流域水文干旱频率分析[J]. 灌溉排水学报,2021, 40(3): 134-141.

LIAO Xianwei, GAO Feng, WEI Ting, et al. Using Copula Method to Analyze Drought Frequency in Songhua River Basin [J]. Journal of Irrigation and Drainage, 2021, 40(3): 134-141.

2020-06-19

国家自然科学基金项目（41501022）；国家科技基础资源调查专项（2017FY100904）；中央高校基本科研业务项目（2452020167）

廖显薇（1998-），女。硕士研究生，主要从事水文干旱研究。E-mail: 1070928072@qq.com

宋小燕（1983-），女。副教授，博士，主要从事水文循环方面的研究。E-mail: xiaoyansong@nwsuaf.edu.cn

责任编辑：韩 洋