基于黏粒量的土壤水分特征曲线预测模型

夏天，田军仓, 2, 3*

·作物水肥高效利用·

基于黏粒量的土壤水分特征曲线预测模型

夏天1，田军仓1, 2, 3*

（1.宁夏大学 土木与水利工程学院，银川 750021；2.宁夏节水灌溉与水资源调控工程技术研究中心，银川 750021；3.宁夏旱区现代农业水资源高效利用教育部工程研究中心，银川 750021）

【】建立基于黏粒量的土壤水分特征曲线预测模型。设计12种不同黏粒量的质量混合比处理，获得一系列合成土样，通过测定合成土样的土壤水分特征曲线，研究了在体积质量一致的条件下，黏粒量对土壤水分特征曲线参数和孔隙分布的影响。在体积质量为1.55 g/cm3条件下，黏粒量增加1.9倍，土壤中传导孔隙（0.03~1 mm）体积减小28.6%，储存孔隙（200 nm~0.03 mm）体积增加6倍，土体的持水性增强。合成土样的土壤水分特征曲线参数s和均与黏粒量显著正线性相关，r与黏粒量显著负线性相关，和均与黏粒量呈指数衰减关系。基于黏粒量确定的土壤水分特征曲线预测模型具有较高的精度，能够快速预测土壤水分特征曲线，预测值与实测值之间相对误差＜15%。

黏粒量；土壤；水分特征曲线；模型

0 引言

【研究意义】土壤水分特征曲线是土壤吸力和含水率之间的定量关系，反映土壤水能量和数量之间的关系，是土壤最重要的水力特性之一[1]。其对于研究和评价土壤的持水性、水分有效性和孔隙分布状况等均具有重要作用，同时也是土壤水分运动和溶质运移动力学模拟的重要参数[2-3]。【研究进展】由于土壤水和介质间的相互作用异常复杂，目前尚不能从理论上推求土壤吸力和含水率之间的关系。为了使用方便，常采用的方法是通过试验测定后采用经验模型对实测数据进行拟合，进而获得水力参数。常用的经验模型有Van Genuchten模型（V-G模型）及其修正模型[4]，Gardner模型[5]，Brooks-Corey模型[6]（BC模型）及Lognormal distribution 模型[7]（LND模型）等。根据毛管理论，土壤水分特征曲线实际上反映的是土壤孔隙状况和含水率之间的关系，因此，任何影响土壤孔隙状况和水分性质的因素都会对土壤水分特征曲线产生影响[8]。为此，许多学者开展了大量试验研究，主要有模型的适宜性研究[9-11]，大孔隙[12]、含盐量[13]、矿化度[9]、生物炭[14]、植物掺混[10]、根系机械作用[3]、农膜残留[11]、施肥种类[15]、砒砂岩风化物[16]、不同地形坡度、构造发育和土地利用类型[14,17-18]、土壤体积质量和机械组成[19-21]等因素对土壤水分特征曲线和水分蓄持能力等的影响研究。针对机械组成这一影响因素，文献[19-20]得到了在概化体积质量一致的条件下，质地因子即黏粒量与土壤水分蓄持能力各指标之间的定量关系，能够为田间土壤水分管理和利用提供合理依据。另一方面，文献[21]得到了在干体积质量一致的条件下，利用沙壤土黏粒量预测土壤水分入渗特性的模型，能够为沙壤土入渗特性的预报提供理论依据。【切入点】但是针对不同黏粒量对土壤孔隙分布的影响、黏粒量与土壤水分特征曲线各参数之间的定量关系，以及基于黏粒量的土壤水分特征曲线预测模型的研究却鲜有报道。

【拟解决的关键问题】针对上述问题，兹采用黏粒质量百分比不同的一系列合成土壤，通过测定合成土壤的土壤水分特征曲线，研究质地因子即黏粒量对土壤水分特征曲线和孔隙分布的影响，得到黏粒量与土壤水分特征曲线各参数之间的定量关系，并推求基于黏粒量的土壤水分特征曲线预测模型，旨在为土壤水分运动数值模拟提供依据。

1 材料与方法

1.1 供试材料

供试土样取自贺兰山东麓沙土地表层土壤（0~20 cm）。土样取回后经纯水洗盐，风干、晾晒、碾压并过2 mm筛备用。采用Bettersize-2003型激光粒度分布仪测定其颗粒粒径组成，其中黏粒（＜0.002 mm）的质量分数为7.48%，粉粒（0.002~0.02 mm）的质量分数为7.13%，砂粒（0.02~2 mm）的质量分数为85.39%，根据国际制土壤质地分类标准，供试土壤质地为沙土。土样的初始含水率为2.97%。原状土的干体积质量为1.55 g/cm3。

1.2 试验设计及方法

试验土样采用人工合成的方法制备。具体操作为：以0.074 mm为筛底，采用电动振筛机，将供试土样筛分为粒径＜0.074 mm和介于0.074~2 mm二个组分，分别记为组1和组2。将组1和组2的土样进行混合，设计12种不同黏粒量的质量混合比，即得到一系列合成土壤。通过测定该系列合成土壤的土壤水分特征曲线，分析黏粒量对不同处理土壤水分特征曲线的影响，并得到黏粒量与土壤水分特征曲线各参数之间的定量关系，推求基于黏粒量的土壤水分特征曲线预测模型。组1和组2的颗粒粒径分布见表1，各处理土壤质量混合比和颗粒粒径分布见表2。

表1 组1和组2的颗粒粒径分布

1.3 试验测定及计算项目

试验在宁夏大学土木与水利工程学院土壤物理实验室内进行。土壤水分特征曲线测定装置采用美国SEC公司生产的1500-F1型压力薄膜仪。开始测定前，将预先配制好的各处理土样分别混合均匀，并按照体积质量1.55 g/cm3均匀压实回填于体积为100 cm3的环刀内，环刀内壁预先均匀涂抹1层凡士林。将回填完成的环刀样浸泡在蒸馏水中24 h至饱和后，取出控水5 min[11]，随后放入压力薄膜仪中，测定脱湿过程的土壤水分特征曲线，压力设定范围为：10~6 000 cm水柱。测定时，随着土样中黏粒（＜0.002 mm）百分量的增加，相应地增加最大加压压力值。试验结束后，将环刀样置于烘箱内，105 ℃恒温烘干24 h后秤取其质量，计算各压力下土壤的质量含水率，并换算为相应的体积含水率。每个处理设3次重复，取均值作为试验结果。

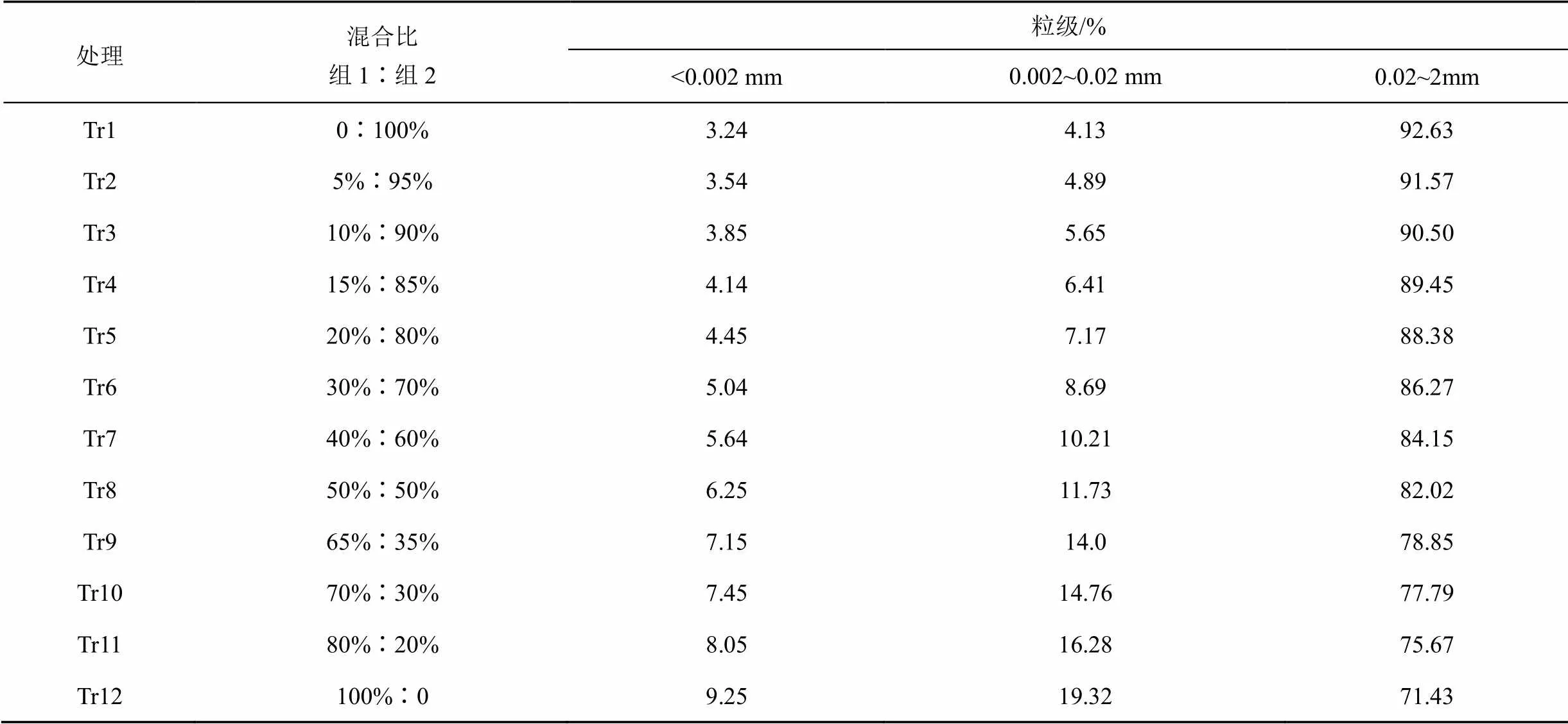
表2 合成土壤质量混合比和颗粒粒径分布

根据土壤的毛管理论，若将土壤中的孔隙假想为各种孔径的圆形毛管，那么土壤水吸力和毛管直径的关系[1]可以表示为：

=3×10-5/， （1）

式中：为土壤水吸力（m）；为当量孔径（m）。

根据土壤水吸力值，可由式（1）计算出相应的当量孔径，反映土壤中不同大小孔隙的分布。若土壤含水率1、2对应的当量孔径分别为1、2，则土壤中孔径在2和1之间的孔隙所占的体积与孔隙总体积之比为2−1（2＞1）[1]。因此，可根据不同处理土壤水分特征曲线的变化，分析各处理土壤孔隙大小分布的变化。

数据处理和图像绘制采用Origin 2017，统计分析采用Excel 2010。

2 结果与分析

2.1 不同处理土壤水分特征曲线

不同处理土壤水分特征曲线如图1所示。从图1可以看出，12种处理土壤水分特征曲线形态基本相同。不同吸力段具体表现为：当土壤水吸力在10~30 cm水柱之间时，各处理土壤含水率均呈快速降低的趋势，土壤水分特征曲线较陡，比水容重较大。此吸力段土壤排水主要在当量孔径0.1~0.3 mm的孔隙内进行。随着黏粒（＜0.002 mm）量的增加，Tr1—Tr6各处理土壤水分特征曲线差异不明显，Tr7—Tr12各处理土壤水分特征曲线平行，比水容重基本相同，且随着黏粒量的增加，相同吸力下Tr7—Tr12处理土壤含水率依次增加，即土壤的持水性依次增强。当土壤水吸力在30~100 cm水柱之间时，随着黏粒量的增加，各处理间差异开始显现，表现为相同吸力下Tr1—Tr12处理土壤的持水性依次增强。此吸力段土壤排水主要在当量孔径0.03~0.1 mm的孔隙内进行。当土壤水吸力在100~2 000 cm水柱之间时，随着黏粒量的增加，相同吸力下Tr1—Tr12处理土壤含水率仍依次增加，即持水性依次增强，但不同处理间差异随着吸力增加而逐渐减小。其中Tr1—Tr6处理土壤水分特征曲线在吸力为700 cm水柱时趋于水平，接近重合，Tr7—Tr8处理在吸力为1 800 cm水柱时接近重合。此阶段排水主要在当量孔径0.001 5~0.03 mm的孔隙内进行。当土壤水吸力在2 000~6 000 cm水柱之间时，随着黏粒量的增加，相同吸力下Tr9—Tr12处理土壤的持水性仍依次增强，但处理间差异随着吸力增加而逐渐减小，最终各处理土壤水分特征曲线均趋于平缓。此阶段排水主要在当量孔径0.000 5~0.001 5 mm的孔隙内进行。以上结果表明，在容重一致的前提下，同一土壤水吸力下，随着土壤中黏粒量的增加，土壤的含水率增加，故在一定吸力范围内，黏粒量的增加对土壤孔隙结构产生一定影响，提高了土体的保水能力。

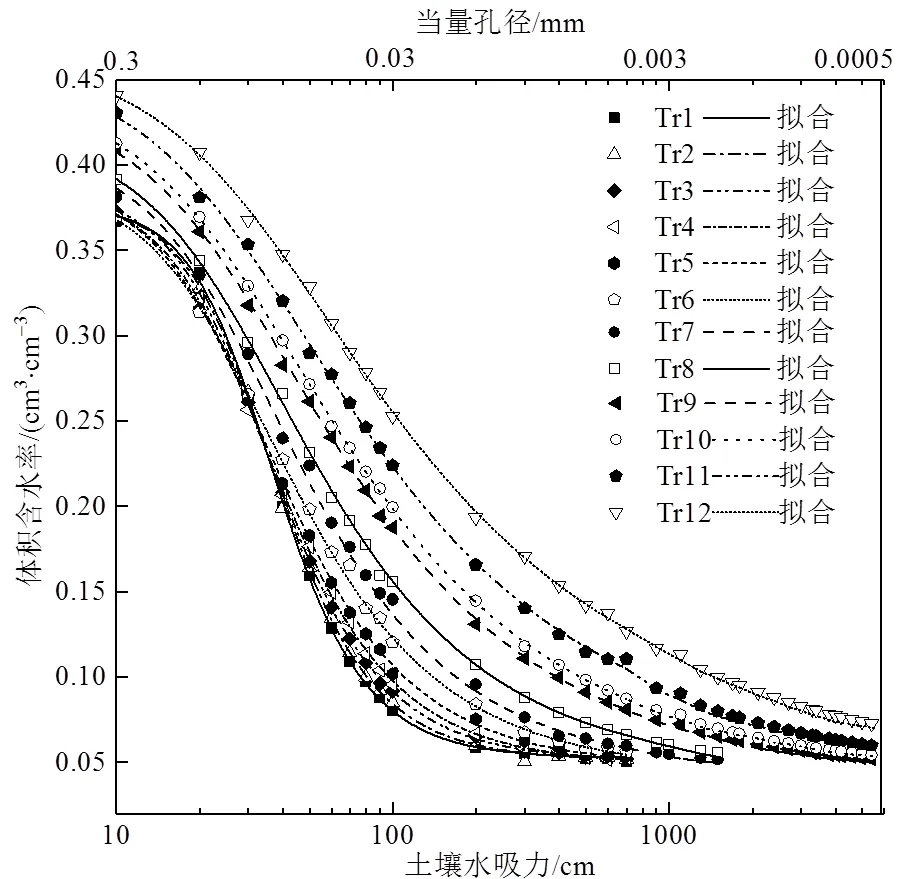
图1 不同处理土壤水分特征曲线

2.2 不同处理土壤当量孔径

土壤水分特征曲线可以间接反映土壤孔隙大小的分布状况[1]。由图1可知，当土壤水吸力在10~30 cm水柱之间时，对应当量孔径为0.1~0.3 mm，此阶段Tr1—Tr6处理土壤水分特征曲线差异很小，比水容重相近，表明在此吸力段范围内Tr1—Tr6处理土壤孔隙结构相近。Tr7—Tr12处理土壤水分特征曲线平行，比水容重相同，表明在此吸力段Tr7—Tr12处理当量孔径为0.1~0.3 mm的孔隙比例基本相同。土壤水吸力在30~100 cm水柱之间时，对应当量孔径为0.03~0.1 mm，其中Tr7—Tr12处理土壤水分特征曲线平行，比水容重相同，表明在此吸力段Tr7—Tr12处理当量孔径为0.03~0.1 mm的孔隙比例基本相同，约占总孔隙体积的13%。由含水率变化可知，Tr6处理当量孔径为0.03~0.1 mm的孔隙体积约占总孔隙体积的14%，Tr5—Tr1处理相应孔隙体积占总孔隙体积的比率依次为15.9%、16.9%、17.1%、18.0%，和18.2%。土壤水吸力在100~200 cm水柱之间时，对应当量孔径为0.015~0.03 mm，各处理土壤水分特征曲线基本平行，比水容重差异较小，表明在此吸力段各处理当量孔径为0.015~0.03 mm的孔隙比例基本相同。土壤水吸力在200~700 cm水柱之间时，对应当量孔径为0.004 3~0.015 mm，其中Tr7—Tr12处理土壤水分特征曲线平行，比水容重相同，表明在此吸力段Tr7—Tr12处理当量孔径为0.004 3~0.015 mm的孔隙比例基本相同，约占总孔隙体积的5.6%。由含水率变化可知，Tr6处理相应当量孔径的孔隙体积约占总孔隙体积的2.81%，Tr5—Tr1处理的比率则依次为2.2%、1.7%、1.3%、0.83%和0.8%。土壤水吸力在700~1 850 cm水柱之间时，对应当量孔径为0.001 6~0.004 3 mm，其中Tr7—Tr12处理土壤水分特征曲线基本平行，比水容重相同，表明在此吸力段Tr7—Tr12处理当量孔径为0.001 6~0.004 3 mm的孔隙比例基本相同。土壤水吸力在1 850~6 000 cm之间时，对应当量孔径为0.000 5~0.001 6 mm，Tr9—Tr12处理土壤水分特征曲线基本平行，即在此吸力段Tr9—Tr12处理当量孔径为0.000 5~0.001 6 mm的孔隙比例基本相同。

以上结果表明，在体积质量一致的前提下，当黏粒量增加1.9倍，土壤中当量孔径0.03~0.1 mm孔隙的体积减小28.6%，当量孔径0.004 3~0.015 mm孔隙的体积增加6倍。根据文献[1]，土壤中当量孔径0.03~1 mm的孔隙为传导孔隙，当量孔径200 nm~0.03 mm的孔隙为储存孔隙。故由上述结果可知，当土壤黏粒量增加1.9倍，传导孔隙的体积减小28.6%，储存孔隙的体积增加6倍。当饱和土体受到吸力作用时，传导孔隙体积的减少和储存孔隙体积的增加，使得土体在同一吸力下排出的水更少，从而提高了土体的持水性。

2.3 黏粒量与土壤水分特征曲线参数的关系

采用V-G模型拟合各处理土壤水分特征曲线。该模型[4]表述为：

=r+(s-r)/[1+()]， （2）

表3 各处理土壤水分特征曲线参数

由表3可知，各处理决定系数2均在0.99以上，且统计分析结果表明，各处理回归值均小于0.01，回归效果显著，即采用V-G模型可以很好地描述本试验条件下土壤的水分特征曲线。从表3的拟合结果还可以看出，随着黏粒量的增加，参数s呈增加的趋势，r呈减小的趋势，呈增加的趋势，和均呈减小的趋势。分别对黏粒量与各参数之间的关系进行拟合，其中为黏粒量（%），拟合结果如表4所示，可由推求得到。

表4 土壤水分特征曲线参数与黏粒量的关系

把表4的拟合结果带入模型（2）中，即可得到基于黏粒量的土壤水分特征曲线预测模型，如式（3）所示，其中为黏粒量（%）。

2.4 模型预测和验证

利用供试土样，将组1和组2按照任意质量比混合，得到合成土样，测得该土样黏粒（＜0.002 mm）的质量分数为6.12%，粉粒（0.002~0.02 mm）的质量分数为11.44%，砂粒（0.02~2 mm）的质量分数为82.44%。测定该土样的土壤水分特征曲线，方法同1.3节所述，并将该土样对应的黏粒百分量代入模型（3）中，预测其土壤水分特征曲线，并与实测值对比，如图2所示。

图2 土壤水分特征曲线实测值和预测值

通过对预测值和实测值之间的相对误差进行计算，得到的结果为：94%的观测点含水率预测值和实测值之间相对误差均＜15%。表明基于黏粒量确定的土壤水分特征曲线预测模型具有较高的预测精度。

3 讨论

在体积质量一致的前提下，同一吸力下，随着土壤中黏粒量的增加，土壤的含水率增加，即土体的保水能力增强。产生这种现象是因为随着黏粒量增加，即土壤质地由粗变细时，土体内细小孔隙数量增多，而使土体的持水性逐渐增强[19]；另一方面，黏粒粒径十分细小，粒径为2 μm的颗粒其比表面积（1.13×103m2/kg）是粒径为2 mm的颗粒比表面积（1.13 m2/kg）的1 000倍[1]，正是这种比表面积的巨大差异，使得随着黏粒量的增加，土体的总比表面积增大而吸附能力增强。本试验供试土壤为沙土，砂粒量较多而黏粒量很少，土体的总比表面积相对较小，黏粒量的微小增加会使比表面积有较为明显的增大，而使土体的吸附能力有较为明显的提高，并且随着黏粒量增加这种趋势愈加明显，因此Tr1—Tr12处理土壤的持水性依次增强。

合成土壤水分特征曲线参数s与黏粒量正相关，此结果与文献[19]得到的结果一致。另一方面，参数r、和分别与黏粒量负相关、正相关和负相关，而文献[19]得到的结果中，在不同的概化体积质量下，随着黏粒量的增加，r、和却有增有减，这与本试验得到的结果不一致。究其原因，可能是由于测定土壤水分特征曲线时装填体积质量的设定方法不同所致。文献[19]用于配制试验土样的各组分土样来源不同，各组分土样固相颗粒密度差异较大，故采用了概化体积质量进行土样装填。而本试验中，用于配制试验土样的各组分来源相同，各组分固相颗粒密度相同，故土样装填体积质量与原状土的体积质量相同，这样就能够最大限度地保证各土样与原状土的总孔隙度相近，而将黏粒量小幅度增加对土壤水分特征曲线各参数的影响体现出来。

4 结论

1）在体积质量为1.55 g/cm3的条件下，黏粒量增加1.9倍，土壤中传导孔隙（0.03~1 mm）体积减小28.6%，储存孔隙（200 nm~0.03 mm）体积增加6倍。

2）土壤水分特征曲线参数s和均与黏粒量显著正线性相关，r与黏粒量显著负线性相关，和均与黏粒量呈指数衰减关系。

3）得到的基于黏粒量的土壤水分特征曲线预测模型具有较高的预测精度，能够快速预测土壤水分特征曲线，预测值和实测值之间相对误差＜15%。

[1] MARSHALL T J, HOLMES J W, ROSE C W. Soil Physics[M]. UK: Cambridge University Press, 1999: 29-36.

[2] 雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京: 清华大学出版社, 1988.

[3] 马昌臣, 王飞, 穆兴民, 等. 小麦根系机械作用对土壤水分特征曲线的影响[J]. 水土保持学报, 2013, 27(2): 105-109.

MA Changchen, WANG Fei, MU Xingmin, et al. Effect of the mechanical action of wheat roots on soil water characteristic curve[J]. Journal of Soil and Water Conservation, 2013, 27(2): 105-109.

[4] VAN GENUCHTEN M Th. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898.

[5] GARDNER W R, HILLEL D, BENYAMIN Y. Post-irrigation movement of soil water: 2. Simultaneous redistribution and evaporation. Water Resources Research, 1970, 6(4): 1 148-1 153.

[6] BROOKS R H, COREY A T. Hydraulic properties of porous media[R]. Hydrology Paper 3, Colorado State University, Fort Collins, 1964.

[7] KOSUGI K. Lognormal distribution model for unsaturated soil hydraulic properties[J]. Water Resources Research, 1996, 32(9): 2 697-2 703.

[8] 邵明安, 王全九, 黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006: 67-68.

[9] 栗现文, 周金龙, 靳孟贵, 等. 高矿化度土壤水分特征曲线及拟合模型适宜性[J]. 农业工程学报, 2012, 28(13): 135-141.

LI Xianwen, ZHOU Jinlong, JIN Menggui, et al. Soil-water characteristic curves of high-TDS and suitability of fitting models[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(13): 135-141.

[10] 郑健, 王燕, 蔡焕杰, 等. 植物混掺土壤水分特征曲线及拟合模型分析[J]. 农业机械学报, 2014, 45(5): 107-112.

ZHENG Jian, WANG Yan, CAI Huanjie, et al. Soil-water characteristic curves of soil with plant additive and analyses of the fitting models[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 107-112.

[11] 王志超, 李仙岳, 史海滨, 等. 含残膜土壤水分特征曲线模型构建[J]. 农业工程学报, 2016, 32(14): 103-109.

WANG Zhichao, LI Xianyue, SHI Haibin, et al. Water characteristic curve model for soil with residual plastic film[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(14): 103-109.

[12] 冯杰, 郝振纯, 刘方贵. 大孔隙对土壤水分特征曲线的影响[J]. 灌溉排水学报, 2002, 21(3): 4-7.

FENG Jie, HAO Zhenchun, LIU Fanggui. Influences of macropores on soil water retention curve[J]. Irrigation and Drainage, 2002, 21(3): 4-7.

[13] 谭霄, 伍靖伟, 李大成, 等. 盐分对土壤水分特征曲线的影响[J]. 灌溉排水学报, 2014, 33(Z1): 228-232.

TAN Xiao, WU Jingwei, LI Dacheng, et al. Effects of salinity on soil water characteristic curve[J]. Journal of Irrigation and Drainage, 2014, 33(Z1): 228-232.

[14] 魏永霞, 王鹤, 吴昱, 等. 生物炭对不同坡度坡耕地土壤水动力学参数的影响[J]. 农业机械学报, 2019, 50(3): 231-240.

WEI Yongxia, WANG He, WU Yu, et al. Effect of biochar on soil hydrodynamic parameters under different slopes[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(3): 231-240.

[15] 高会议, 郭胜利, 刘文兆, 等. 不同施肥土壤水分特征曲线空间变异[J]. 农业机械学报, 2014, 45(6): 161-165, 176.

GAO Huiyi, GUO Shengli, LIU Wenzhao, et al. Spatial variability of soil water retention curve under fertilization practices in arid-highland of the loess plateau[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6): 161-165, 176.

[16] 张磊, 齐瑞鹏, 张应龙, 等. 砒砂岩风化物对土壤水分特征曲线及蒸发的影响[J]. 土壤学报, 2015, 52(1): 77-86.

ZHANG Lei, QI Ruipeng, ZHANG Yinglong, et al. Effects of amendment of aeolian sandy soil and loess with soft sandstone on soil water retention curve and evaporation[j]. Acta Pedologica Sinica, 2015, 52(1): 77-86.

[17] 邓羽松, 丁树文, 蔡崇法, 等. 鄂东南崩岗剖面土壤水分特征曲线及模拟[J]. 土壤学报, 2016, 53(2): 355-364.

DENG Yusong, DING Shuwen, CAI Chongfa, et al. Characteristic curves and model analysis of soil moisture in collapse mound profiles in Southeast Hubei[J]. Acta Pedologica Sinica, 2016, 53(2): 355-364.

[18] 宁婷, 郭忠升, 李耀林. 黄土丘陵区撂荒坡地土壤水分特征曲线及水分常数的垂直变异[J]. 水土保持学报, 2014, 28(3): 166-170.

NING Ting, GUO Zhongsheng, LI Yaolin. Soil water characteristic curves and soil water constants at different depths in the abandoned sloping field of loess hilly region[J]. Journal of Soil and Water Conservation, 2014, 28(3): 166-170.

[19] 李卓, 吴普特, 冯浩, 等. 容重对土壤水分蓄持能力影响模拟试验研究[J]. 土壤学报, 2010, 47(4): 611-620.

LI Zhuo, WU Pute, FENG Hao, et al. Simulated experiment on effects of soil bulk density on soil water holding capacity[j]. Acta Pedologica Sinica, 2010, 47(4): 611-620.

[20] 李卓. 土壤机械组成及容重对水分特征参数影响模拟试验研究[D]. 杨凌: 西北农林科技大学, 2009.

LI Zhuo. Simulated experiment on effects of soil mechanical composition and soil bulk density on soil water characteristic parameters[D]. Yangling: Northwest A & F University, 2009.

[21] 夏天, 田军仓. 基于沙壤土黏粒量预测土壤水分入渗量和湿润锋深度[J]. 灌溉排水学报, 2020, 39(11): 90-96.

XIA Tian, TIAN Juncang. Using clay content to predict water infiltration in sandy loam soils[J]. Journal of Irrigation and Drainage, 2020, 39(11): 90-96.

Using Clay Content to Estimate Soil Water Characteristic Curve

XIA Tian1, TIAN Juncang1,2,3*

(1. School of Civil and Hydraulic Engineering, Ningxia University, Yinchuan 750021, China; 2. Ningxia Research Center of Technology on Water-saving Irrigation and Water Resources Regulation, Yinchuan 750021, China; 3. Center of Engineering Research on Efficient Utilization of Water Resources in Modern Agriculture in Arid Regions (Ministry of Education), Yinchuan 750021, China)

【】Water retention curve is a parameter describing the ability of a soil to hold water; it is modulated by soil structure and texture. The aim of this paper is to evaluate the feasibility of using clay content to estimate water retention curve of a sandy soil.【】The sandy soil used in the experiment was sieved to two groups first, and 12 soils with different clay contents were made by thoroughly mixing soils taken from the two groups at different mass fractions. The water retention curve of each sample was measured in laboratory, from which we calculated the pore size distribution and analyzed the impact of the clay content.【】When bulk density was 1.55 g/cm3, increasing clay content by 1.9 times led to a 28.6% decrease in volume of pores with diameters in the range of 0.03~1 mm, and six times increase in volume of pores with diameter in the range of 200 nm~0.03 mm. Fitting the curves to the van Genuchten formula showed that the parameterssandin the formula werepositively proportional to the clay content, while the parameterrwas negatively proportional to the clay content; the parameter n in the formula decreased exponentially with the clay content.【】There were close correlations between all parameters in the van Genuchten formula and the clay content in the sandy soil we studied. These correlations, along with the van Genuchten formula, can be used to estimate the water retention curve of the sandy soil after its clay content changes due to cultivation and/or erosion. For all soils with different clay contents we studied, the absolute errors between the estimated and the observed water contents were less than 15%. These results have implications for numerical simulation of water flow and solute transport in these soils.

clay content; soil; water characteristic curve; model

S152.3

A

10.13522/j.cnki.ggps.2019243

1672 - 3317（2021）03 - 0009 - 06

夏天, 田军仓. 基于黏粒量的土壤水分特征曲线预测模型[J]. 灌溉排水学报, 2021, 40(3): 9-14.

XIA Tian, TIAN Juncang. Using Clay Content to Estimate Soil Water Characteristic Curve[J]. Journal of Irrigation and Drainage, 2021, 40(3): 9-14.

2020-09-10

国家自然科学基金项目（51869024）；宁夏自治区重点研发计划重大项目（2018BBF02022）；宁夏高等学校一流学科建设项目（NXYLXK2017A03）

夏天（1988-），女。博士研究生，主要从事节水灌溉理论与技术研究。E-mail: 359659709@qq.com

田军仓（1958-），男。教授，博士生导师，主要从事节水灌溉理论与技术研究。E-mail: slxtjc@163.com

责任编辑：白芳芳