基于可拓层次分析的机器人系统安全评价方法*

刘 旭，王 颂，于洪鹏，李志海

(1. 南方电网科学研究院有限责任公司，广州 510080； 2. 中国科学院沈阳自动化研究所，沈阳 110016； 3. 中国科学院机器人与智能制造创新研究院，沈阳 110169)

0 引言

电力作为中国能源战略转型的重点，是国民经济和民生保障的基础，智能电网建设要求对电力系统的发、输、配、用各个环节进行有效地维护，以保证电网的可靠、连续运行。在此要求下，电力机器人市场应运而生，机器人自动化监控操作越来越多地应用在电力系统工作现场，确保电力系统安全稳定不间断运行。而电网场所中的高压等复杂环境，对电力机器人的安全性提出了更高要求，对电力机器人系统的安全评价显得尤为重要[1]。目前我国尚缺乏电力机器人全生命周期的国家标准，尤其是安全评价方面的标准[2]。机器人行业中，以往的安全评价方法多针对工业机器人，但其结果无法兼顾定性和定量的评价[3-4]。而在电力行业的设备中，通常采取在模糊层次分析法的基础上研究新的评价方法，对配电运行、设备状态、设备效能及安全性等进行评价[5]。典型的有云南电网公司针对输电线路鸟害故障的风险评估，建立了鸟害风险评估层次结构模型，最终建立输电线路鸟害故障风险评估模型，消除了传统评价中主观性强、数据繁杂的缺点[6]。

综上所述，文中针对电力机器人采用可拓层次分析，将可拓学的基元理论、共轭分析理论以及可拓分析理论与多元耦合原理相结合，对安全评价指标进行耦合计算，形成了对电力机器人安全评价进行定性定量分析的有效工具。运用此工具，以电力环境特征为基础，建立安全评价指标集，通过建模解析安全指标权重的形成机理、以及与安全评价结果的量化映射关系，此方法可以提升安全评价的精度，推动电力机器人更加安全化、标准化。

1 基于可拓层次分析的安全评价

依据安全评估国标GB/T 38260-2019《服务机器人功能安全评估》中提出的机器人可能造成的危害，结合电力机器人自身及使用环境的特性，构建机器人系统安全评价指标体系，由8项影响机器人系统安全的指标构成，如图1所示。

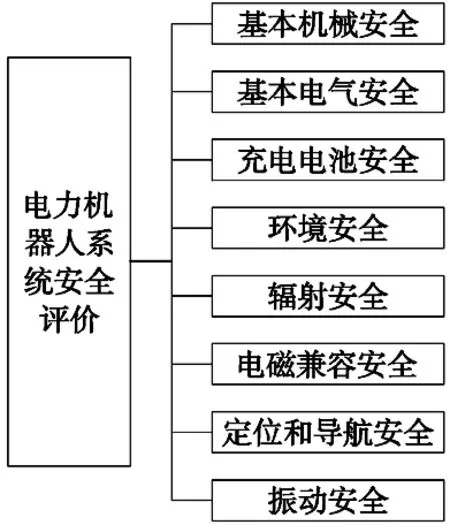
图1 电力机器人系统安全评价指标体系

可拓学评价的关联函数权重计算方法能够实现基于评价指标自身的客观动态计算，可拓学是由蔡文提出用于解决矛盾问题的学科，以形式化的模型，探讨事物拓展的可能性以及开拓创新的规律和方法[7]。它具有形式化、逻辑化和数学化的特点，目前已广泛应用于机器人、无人机领域[8-9]。利用可拓层次分析法能够实现对电力机器人系统整体层次进行定权、评价，从而得到可量化的机器人整体安全评价。

1.1 建立评价指标集

根据建立的机器人系统安全评价体系，对电力机器人系统进行安全评价，首先为评价项目建立一个评价集，记为L={L1,L2,…,Lm}。另外，依据工业及服务机器人风险监测中常用的危险等级划分方法，将机器人系统安全评价等级分为4个等级，记为D={D1,D2,D3,D4}，如表1所示。

表1 机器人评价等级区间标准

1.2 计算可拓区间数与权重

针对于机器人系统安全评价这个目标，利用权重向量来定义评价集内元素对机器人系统整体安全的影响，将评价集内的元素两两进行对比，构造可拓区间数判断矩阵P。

(1)

权重向量的求解步骤为：

(1)将判断矩阵P表示为左右矩阵的形式，即P=[P-,P+]。

(2)分别计算左右矩阵P-,P+的最大特征值λ-,λ+，则λ=[λ-,λ+]为P的区间数特征值，并得到左右矩阵归一化后的特征向量x-,x+。

(3)计算权重系数k、m的值。

(2)

(4)求出P关于λ=[λ-,λ+]的特征向量x，也就是各个指标对机器人系统整体安全的权重W。

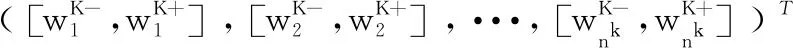
(3)

(4)

则所有指标对电力机器人系统安全评价的归一化权重为:

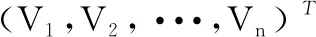
(5)

除了权重值外，还需要求解出各评价指标得分归属于评价等级的隶属度矩阵rij，确定隶属度矩阵的方法有很多，本文选用可拓关联函数得到隶属度矩阵[10]。

(6)

其中，

式中，λ(xi,xmi)-λ(xi,xji)代表第i个评价指标关于第j个等级区间和电力机器人评价集整体区间组成的区间位置关系，λ(xi,xji)代表评价指标xi与第j个评价等级域的距，λ(xi,xmi)代表评价指标xi与电力机器人评价集整体域的距。xji是第j等级关于xi的取值范围，即(aij,bij)，xmi是电力机器人评价集整体关于pi的取值范围。

1.3 系统安全综合评价

由各个评价指标的归一化权重向量U与隶属度矩阵R耦合计算，得到电力机器人系统整体安全评价向量E：

E=UT×R

(7)

通过计算得到整体安全评价向量，但该向量不能直观的反映电力机器人系统的整体安全程度。为了综合权重的全部信息，将评价等级与整体安全评价向量进行耦合计算，得到一个可量化的数据，使评价结果更符合实际需求。假设n个评价等级区间D={D1,D2,…,Dn}，取每个评价区间的最大值，则最终安全评价结果为：

N=E×D

(8)

2 实验验证

以某型号变电站巡视机器人的安全测试为例，设基本机械安全、基本电气安全、充电电池安全、环境安全、辐射安全、电磁兼容安全、定位和导航安全、振动安全8个评价项因素为L={L1,L2,…,L8}，由行业专家对各项打分，得到机器人系统整体安全的可拓区间判断矩阵P。

P=

(9)

2.1 确定权重及隶属度矩阵

利用第1节中的公式，结合式(9)的数据，计算得到电力机器人系统安全中各评价变量值，结果如表2所示。

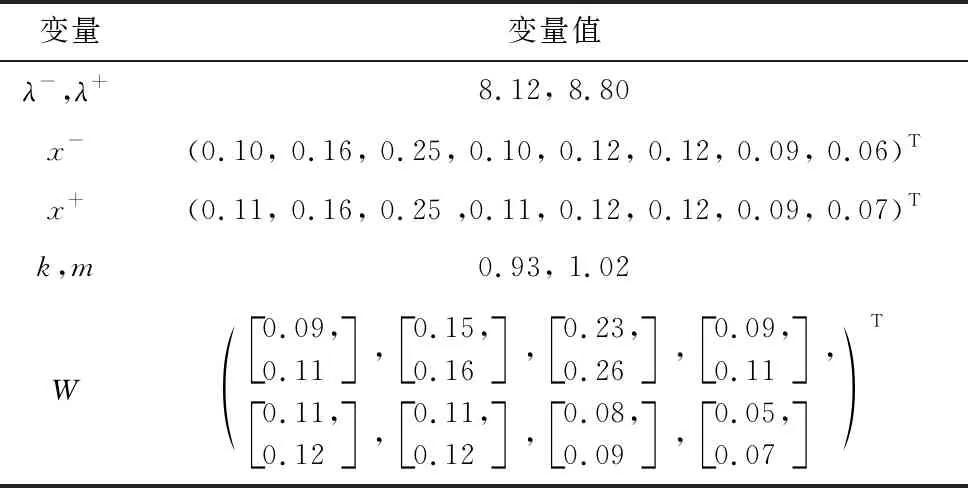
表2 电力机器人系统安全评价变量值

得到各评价因素的权重W后，根据公式将权重向量进行单值化处理和归一化处理，最终得出8个评价项因素对电力机器人系统安全评价的重要程度排序U。

(10)

通过可拓关联函数和该电力机器人各评价指标的得分情况，再利用1.2节中的计算函数，计算得到各评价指标对于综合评价结果的隶属程度，即构造一个隶属度矩阵R，如表3所示。

表3 各评价指标权重及隶属度

2.2 评价结果

综合电力机器人系统安全各个指标的权重，以及本次测试的指标得分相对于评价等级的隶属度矩阵，得到该系统安全评价的整体评价值。

(11)

为了更加直观地表达系统安全评价结果，将得到的向量量化成数值。

N=E×D=0.314 9×25+0.344 8×
50+0.201 9×75+0.142 9×100=54.5

(12)

则该变电站巡检机器人系统的整体安全评价得分为54.5，属于电力机器人评价等级中的低风险等级，与本次测试中行业专家对其系统定性评估出的结果情况一致。然而，传统的组织专家评审的方法耗时耗力，对于实际中大批量的检验需求，传统方法效率低。本文中提出的基于可拓层次分析的机器人系统安全评价方法，可以克服传统方法无法定量给出结果，以及普遍存在着由于主观因素影响评价结果的问题。

3 结论

提出了一种基于可拓层次分析的机器人系统安全评价方法，考虑基本机械安全、基本电气安全、充电电池安全、环境安全、辐射安全、电磁兼容安全、定位和导航安全、振动安全8个因素，建立了机器人系统安全评价体系及评价指标集。以某型号变电站巡检机器人为研究对象，采用可拓层次分析法确定评价指标的权重系数，通过将权重系数与隶属度引入评价体系进行耦合计算，得到可量化的机器人系统安全评价结果，对机器人的安全性能进行了准确的评价。本文提出的机器人系统安全评价方法可以作为机器人安全检测、安全评价及安全认证的理论参考，适用性强、效率高，兼顾了定性与定量分析的特性，减少传统评价方法的主观因素。由于机器人的特殊与部分定性安全指标的存在，目前评价指标体系不能完全反应机器人的安全性，对指标体系的改进是所要关注的方向。