新型分流量解析方程的建立与应用

高文君，殷瑞，高能，盛寒，高志江

（1.中国石油吐哈油田分公司勘探开发研究院，新疆哈密 839009；2.长江大学石油工程学院，武汉 430100；3.中海油能源发展股份有限公司工程技术分公司，天津 300452；4.中国石油测井有限公司大庆分公司，黑龙江大庆 163412）

水驱特征曲线和含水变化规律反映的是注水油藏宏观开发指标变化规律[1]，而含水率与出口端含水饱和度的关系（即分流量解析方程），反映的是油层微观水驱油渗流特征[2]。1941 年，莱文莱特首次提出了分流量方程的计算通式[3]。但莱文莱特提出的并非分流量方程的解析式，只是一个两种非混相流体流动的基本计算公式。为此，油藏工程师常假定地层是平的，毛细管压力梯度可忽略不计，且利用油水相渗比值，将分流量方程简化为解析式来确定含水率与出口端含水饱和度的变化关系。这种处理方式，对于中—高渗油藏在中—高含水阶段水驱机理的研究起到一定的理论指导作用[4-5]，但并不符合特低—低渗或非常规等油藏的油水相渗比值[6-8]，加上毛细管压力非常大，非润湿相还存在一定的启动压力，简化后的分流量解析式很难与实验值实现完全匹配。

20 世纪60—70 年代，前人陆续从已开发油田统计得到了许多水驱特征曲线，如马克西莫夫水驱特征曲线、卡扎科夫水驱特征曲线等[9-10]。此后，中国学者也陆续提出了一些新的水驱特征曲线，如俞启泰水驱特征曲线、张金庆水驱特征曲线等[11-14]。然而，这些水驱特征曲线缺乏正向理论推理过程，只是以经验或统计的形式给出。中国学者也试图实现部分水驱特征曲线的正向理论推理，但一直未找到合适油水相渗比值的关系式，导致这些水驱特征曲线缺乏渗流理论依据的支持。本文利用反向推理技术实现目标较强的特点，先对水驱特征曲线进行微分，直接得到含水变化规律后，再结合韦尔杰（Welge）的平均含水饱和度方程，通过微分求解，得到分流量方程的解析式[15]；若进一步与两相渗流理论中含水率的衍生式——莱文莱特函数相结合，可得到描述两相渗流特征的油水相渗比值与含水饱和度关系式，这也间接地解决了水驱特征曲线理论推导问题。同时，考虑到含水变化规律曲线呈凸形、“S”形或凹形的特点，经对已有水驱特征曲线进行筛选，归纳出了一种新型广义水驱特征曲线，然后再对其进行反向推理，得到更具广泛适应性的分流量解析方程。

1 新型广义水驱特征曲线的确定

1997 年，俞启泰提出了一种广义水驱特征曲线[12]，文献［8］给出了其校正关系式：

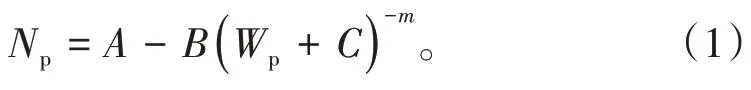
1976 年，卡扎科夫通过对已开发注水油藏进行统计分析，得到了一种水驱特征曲线，简称卡扎科夫曲线，文献［8］给出了其校正关系式：

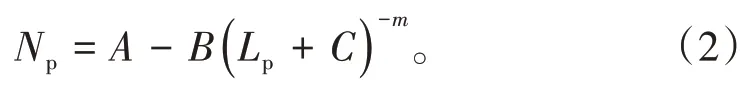
将Lp=Np+Wp代入（2）式，得

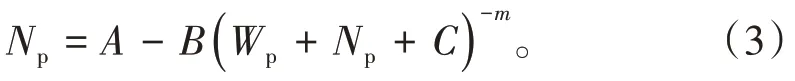
对比（1）式和（3）式，并引入活塞式驱程度指数n（其值越大，水驱油活塞式驱特征越明显[16]），（3）式可写成通式：

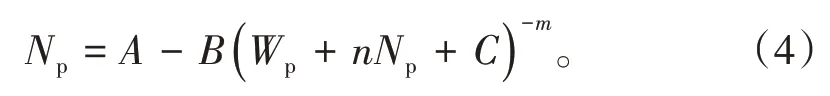
很明显，（4）式中，当n=0时，则转化为（1）式；当n=1 时，则转化为（3）式。因此，（4）式是一个广义水驱特征曲线[17]，（1）式和（3）式只是（4）式的特例。

2 对应含水变化规律的反演

对（4）式两端时间t求导，并结合阶段产油量qo=dNp/dt，阶段产水量qw=dWp/dt，得：

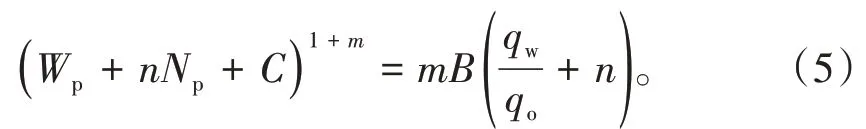
由含水率基本概念式[18]可知：

将（6）式与（5）式结合，得：

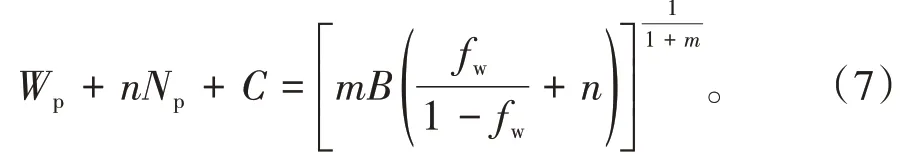
将（7）式代入（4）式，再结合采出程度R=Np/N，并令a=A/N，b=N-1（B/mm）[1/（1+m）]，得广义水驱特征曲线（4）式对应的含水变化规律：

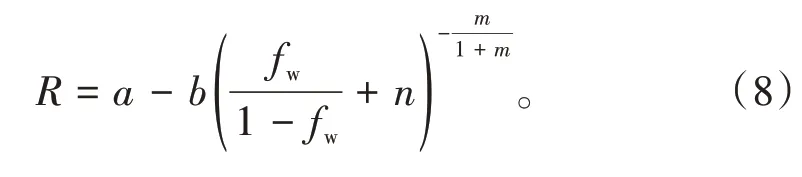
3 新型分流量解析方程的确定

俞启泰曾指出，油水渗流特征实质性关系式为fw～Swe，即分流量方程的解析式，而（8）式实质上只是平均含水饱和度与含水率的变化关系，反映的是油藏宏观生产指标变化规律。因此，油藏在注水保持地层压力的条件下，其平均含水饱和度[3]为

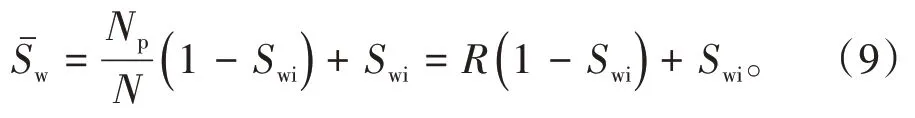
结合Buckley-Leverett 的线性驱替理论，在非活塞式水驱油条件下，Welge方程[3]为

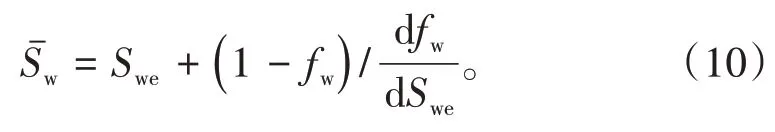
将（9）式代入（10）式，得：

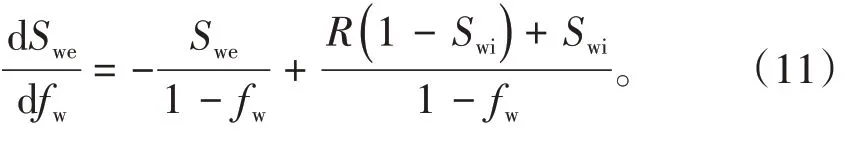
再将（8）式代入（11）式，得：

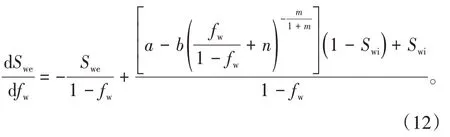
很明显，（12）式属非齐次线性方程。因此，按常数变易法，先求得齐次线性方程dSwe/dfw=-Swe/（1-fw）的通解:

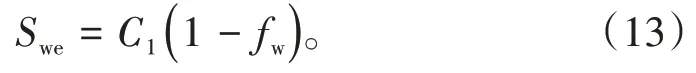
再将（13）式中常数C1换成fw的未知函数u（fw），则得到：

对（14）式求导，得：

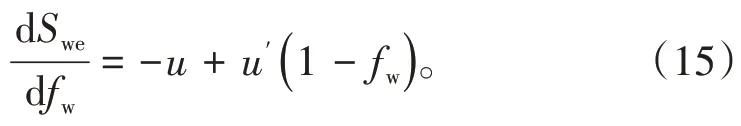
将（14）式代入（12）式左端，结合（15）式，可得：

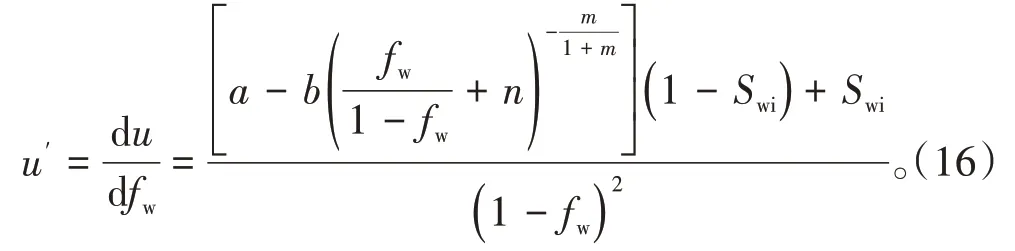
进一步整理（16）式，得：

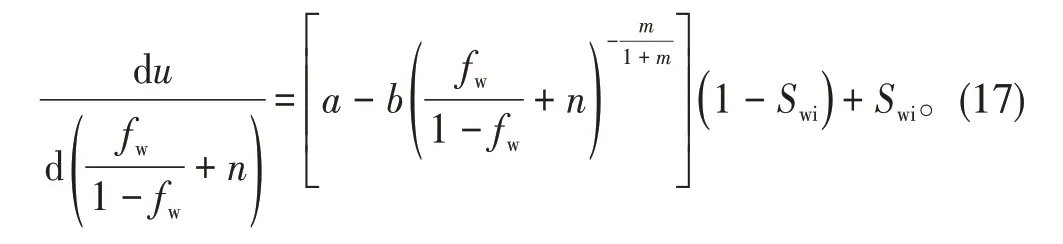
求解（17）式微分方程的解，得：

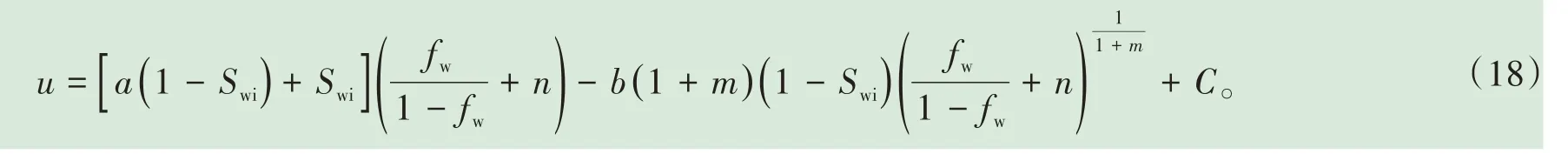
将（18）式代入（14）式，整理之后可得到非齐次线性方程（12）式的通解：

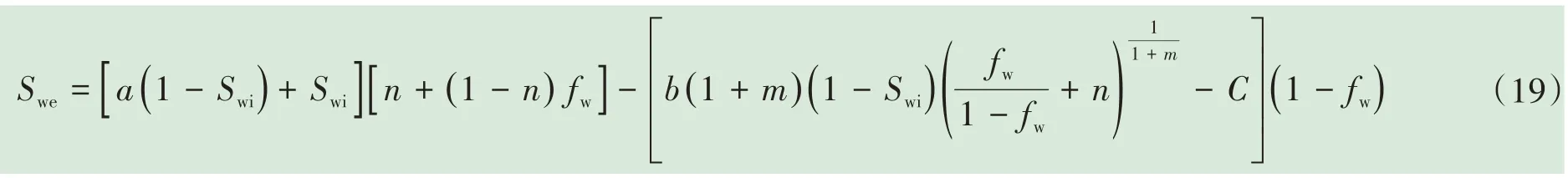
在水驱油过程中，油井刚见水时出口端含水饱和度Swe=Swi，若含水率为0，则

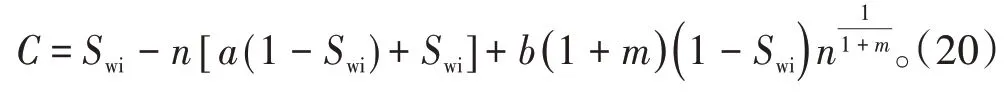
将式（20）代入（19）式，整理得：

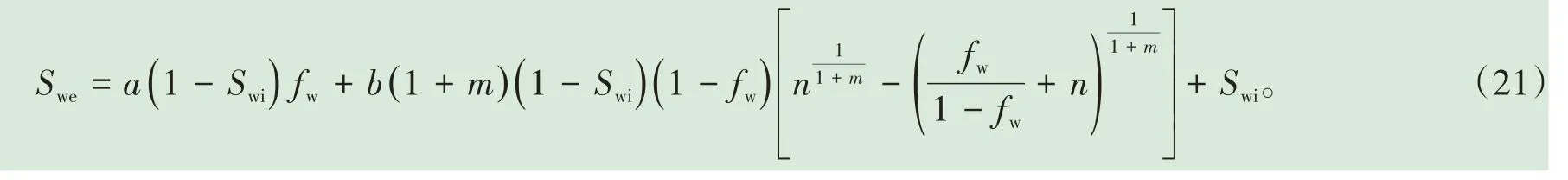
上述在确定分流量方程的解析式过程中，只使用了含水率的概念式，而没有采用传统两相渗流理论中含水率的衍生式——莱文莱特函数，回避了传统方法中需要确定油水相渗比值与含水饱和度的关系式，以及油、水各自流动符合线性流的条件限制[3]。在得到（21）式的基础上，若再结合莱文莱特函数，可直接得到描述油水两相渗流特征方程——油水相渗比值与含水饱和度的关系式：

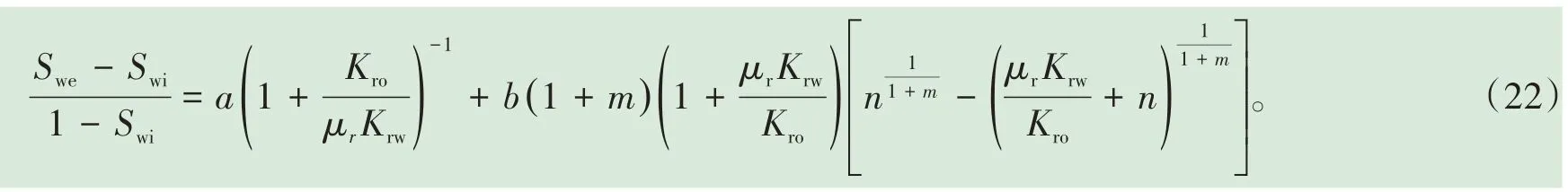
显然，上述油水相渗比值与含水饱和度的关系式很难通过实验数据分析得到，（22）式与分流量解析方程均属超越方程，具有比较特殊的函数结构。若令y=Swe，x1=fw，x2=（1-fw）{nk-[fw/（1-fw）+n]k}，a0=Swi，a1=a（1-Swi），a2=b（1+m）（1-Swi），k=1/（1+m），那么，（21）式转化为多元线性方程：

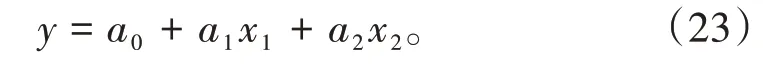
由于x2中含有2 个待定的参数n和k，因此，在拟合时，先给定n的初始值为1，然后求得相关系数最大时的k值；其次，固定前面确定的k值，再求得相关系数最大时的n值；重复前面2个步骤，直至得到拟合相关系数最大时的n和k值，以及对应的a0、a1、a2等待定参数。这种求解方法称为双变量正交求解法，在复杂数学模型分析中经常采用。

利用西峰油田庄19 井区（特低渗致密油藏）、羊二庄油田某区块（块状砂岩底水油藏）、贝尔油田某区块（特低渗复杂砂岩油藏）、榆树林油田东14 区块（低渗裂缝砂岩油藏）的水驱油实验数据[19-22]，分别代入（21）式后，并转化成（23）式进行拟合（表1）。虽然4 个油藏含水率与出口端含水饱和度变化形态差异很大，但拟合效果均很好，相关系数均超过0.999 6，表明分流量解析方程（21）式具有较好的适应性（表2，图1）。

为了进一步对比说明（21）式的精确度，同样，选用传统的含水率与出口端含水饱和度的关系式fw=[1+m0μw/μo·exp（-n0Swe）]-1，对西峰油田庄19 井区、羊二庄油田某区块和贝尔油田某区块和榆树林油田东14 区块的水驱油实验数据进行拟合（表3，图2），结果表明，利用传统指数式，不仅拟合程度较低，而且拟合曲线与实验数据偏差也较大。

进一步对（21）式进行分析，当n=0 时，可得到（1）式水驱特征曲线的分流量解析方程：

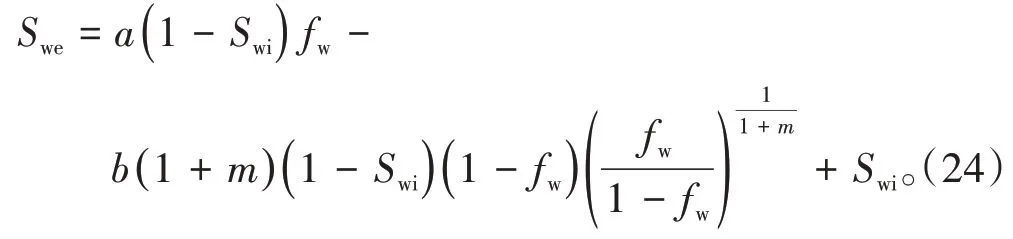
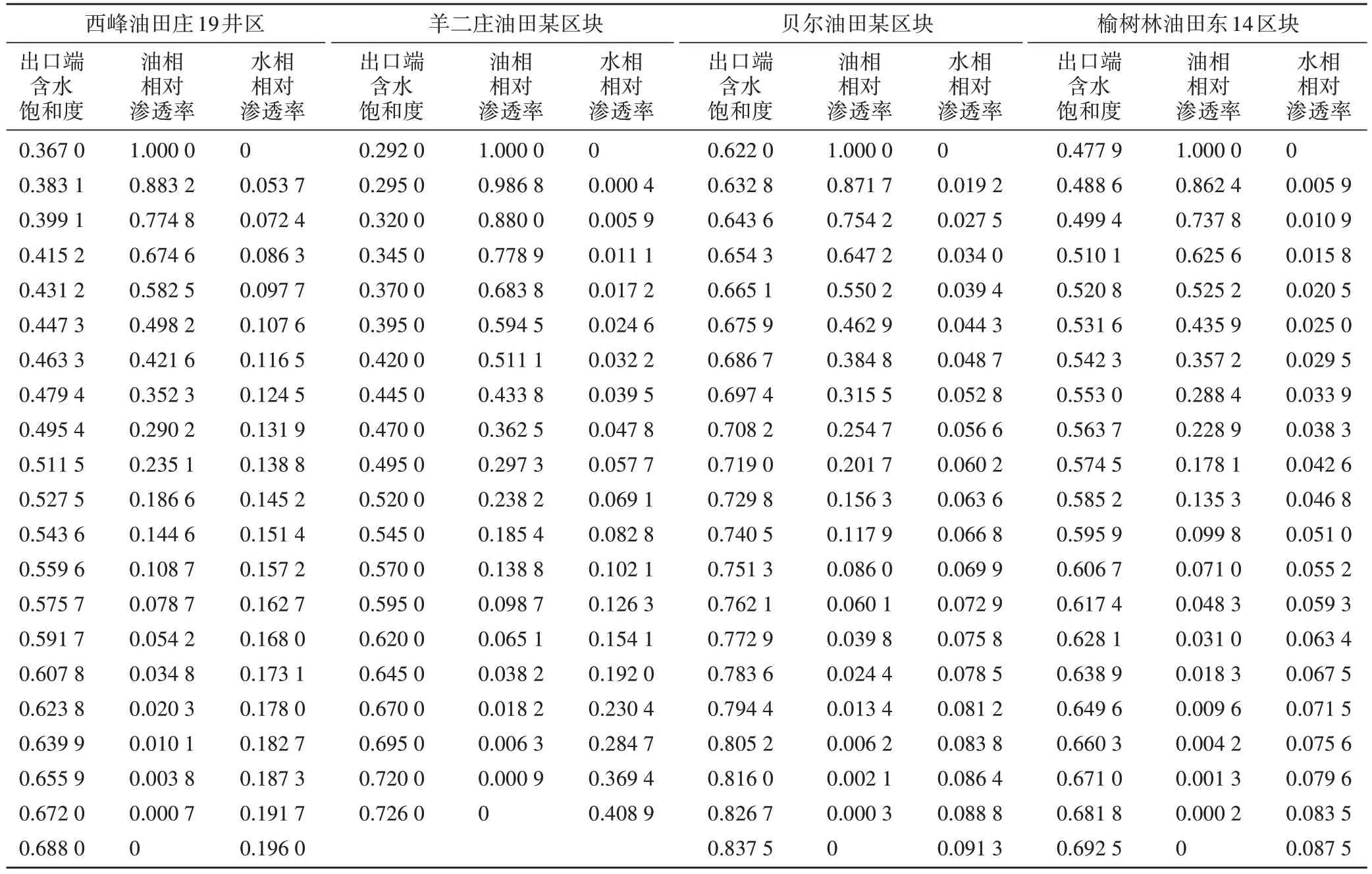
表1 中国4个不同类型油藏油水相渗实验数据Table 1.Experiment data of oil and water permeabilities in four different types of oil reservoirs in China

表2 中国4个油藏水驱油实验数据利用（21）式拟合的结果Table 2.Fitting results of water flooding experiment data from four oilfields in China using equation (21)

当n=1 时，由（21）式可得到（2）式水驱特征曲线的分流量解析方程：

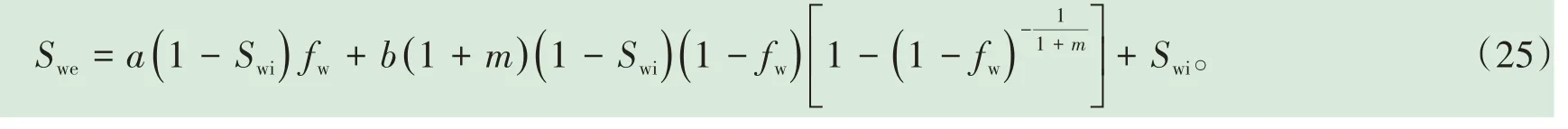
当Swe=1-Sor时，fw=1，代入（25）式，整理之后可以得到参数：

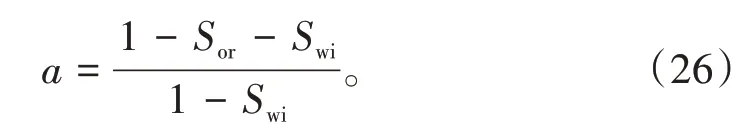
若存在a=b（1+m），则（25）式转化为

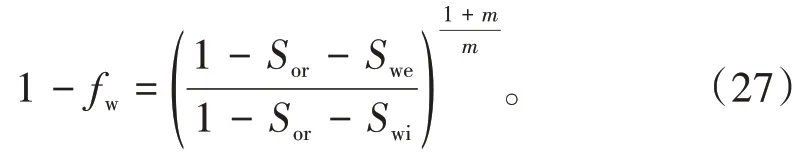
由概念可知出口端含油率：

取m=0.5，μr（1-Sor-Swi）=50，那么，必然存在艾富罗斯两相渗流实验结果[3]：

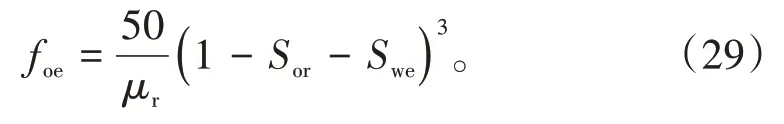
因此，艾富罗斯实验结果是（21）式在特定条件下的一种特殊情况，不仅要符合Swe=Swi时，fw=0；Swe=1-Sor时，fw=1 等初始边界条件，而且还要满足a=1.5b和μr（1-Sor-Swi）=50等特殊条件约束。

4 对应含水变化规律适应性分析

一般对（8）式取fw=0.98，得到最终水驱采收率为

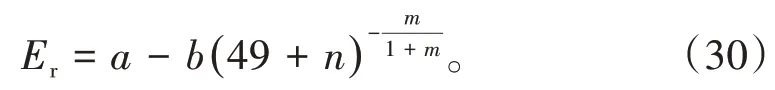
将（8）式除以（30）式，可得水驱可采储量采出程度关系式：

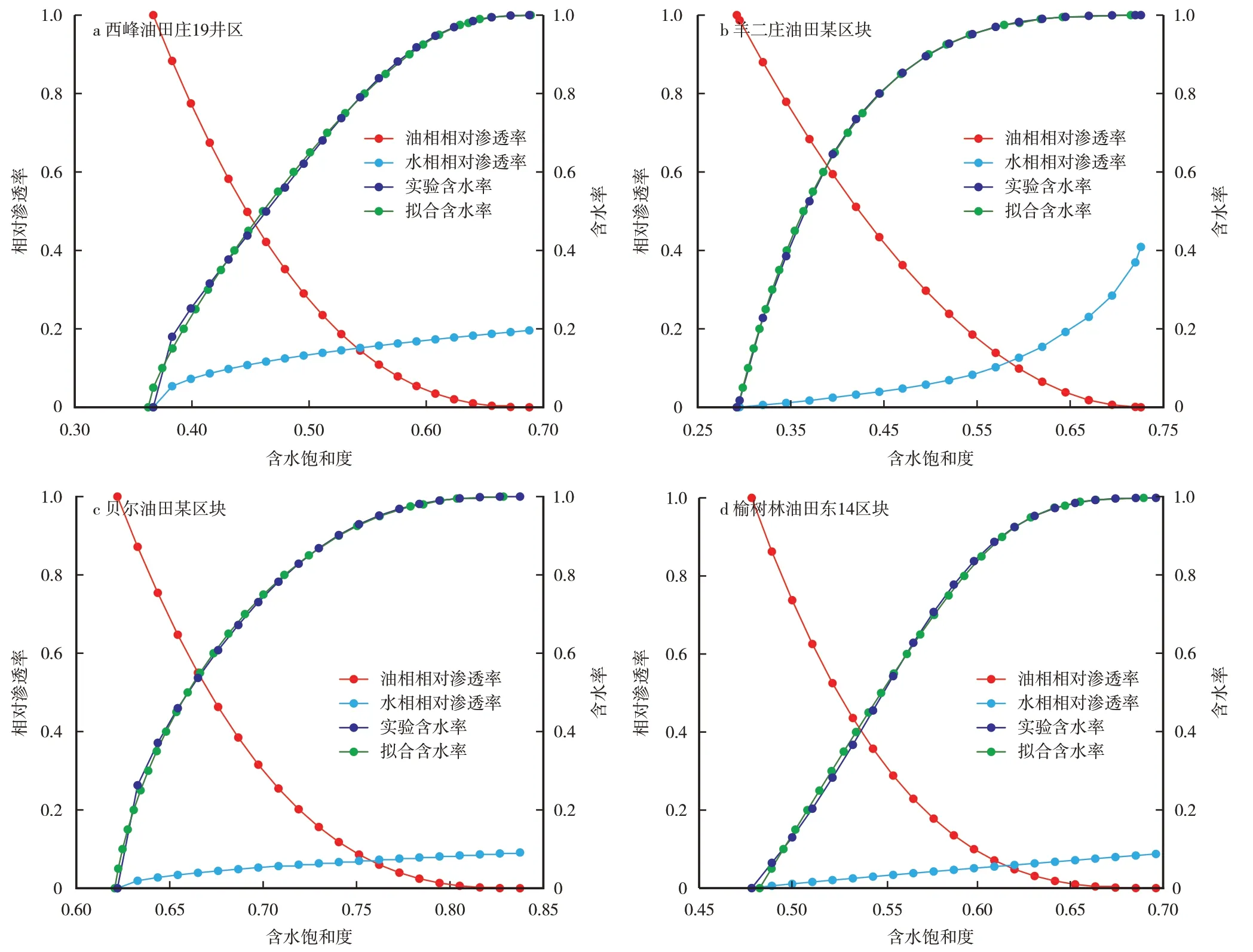
图1 中国4个油藏利用（21）式拟合的分流量变化曲线Fig.1.Variations of fractional flow fitted by equation(21)in four reservoirs in China

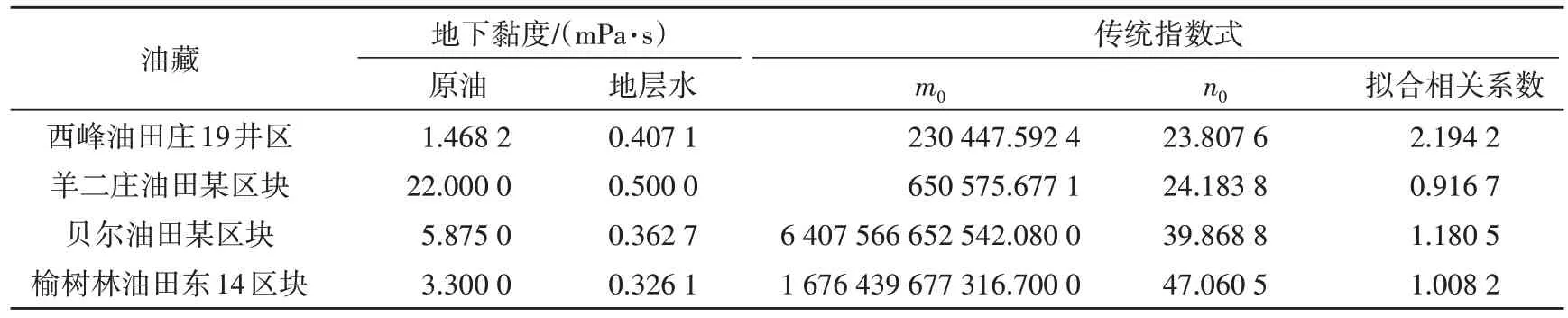
表3 中国4个油藏水驱油实验数据利用传统指数式拟合的结果Table 3.Fitting results of water flooding experiment data from four oil reservoirs in China using traditional exponential formula

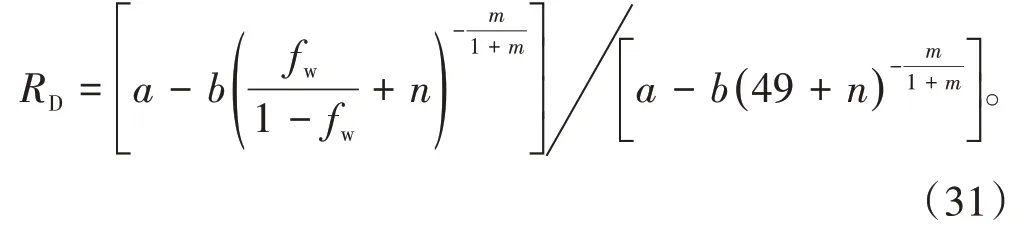
令a1=a/[a-b(49+n)-m/（1+m）]，b1=b/[a-b(49+n)-m/（1+m）]，代入（31）式，可得

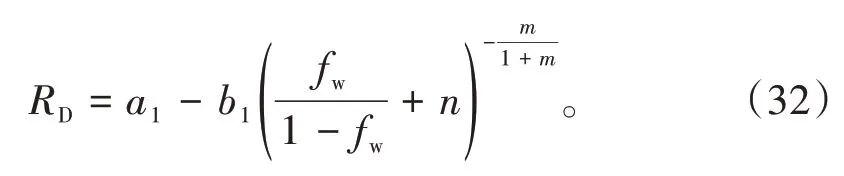
按表4 中给定的参数，可得到2 组描述凹形、“S”形和凸形含水变化规律曲线。这说明（8）式不仅可以描述凹形、“S”形和凸形等含水变化规律曲线，而且也可以描述无水期为0或不为0的各种形态含水变化规律曲线（图3）。

同样，令y=RD，x=-[fw/（1-fw）+n]-m/（1+m），则（32）式转化为一元一次线性方程：

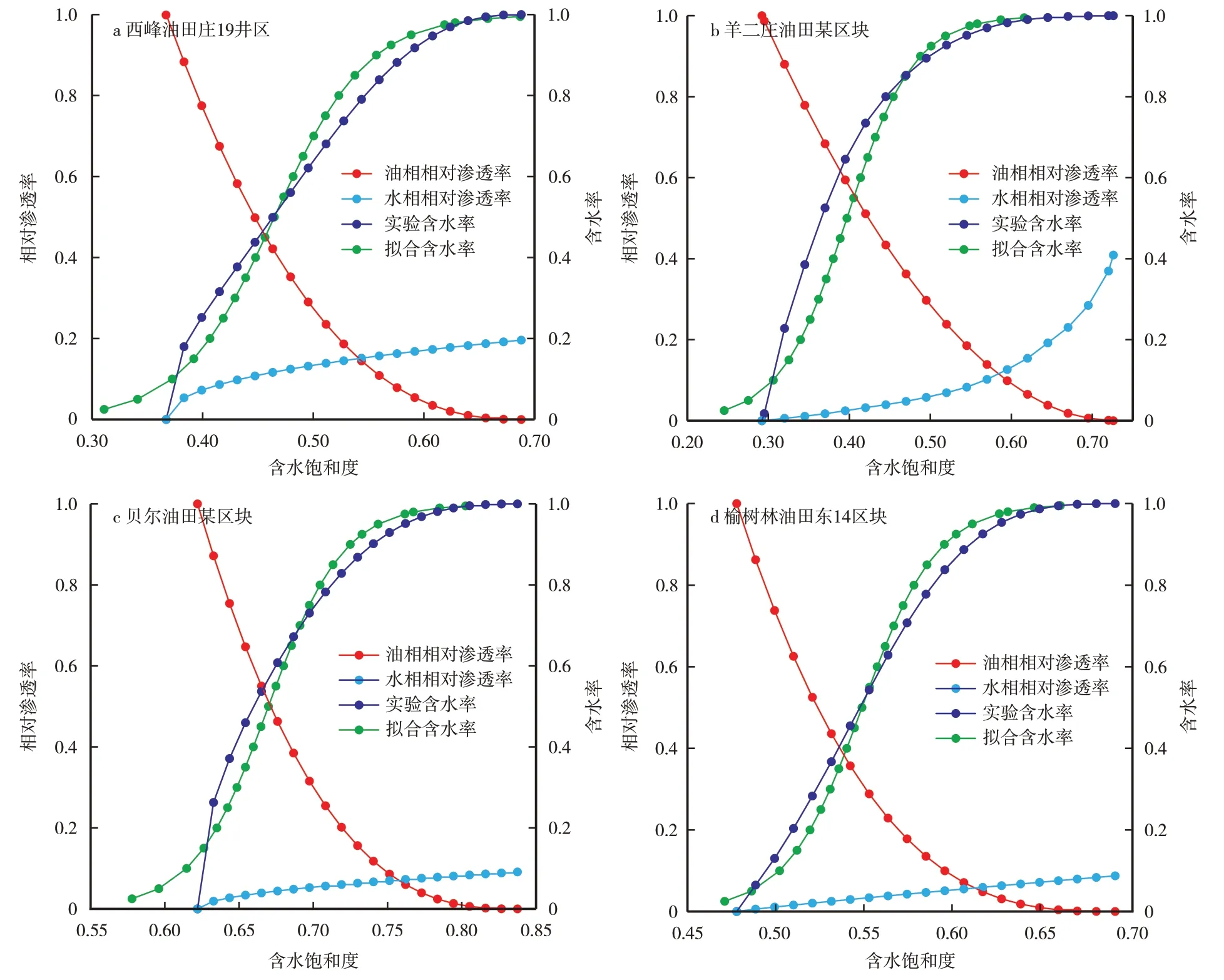
图2 中国4个油藏利用传统指数式拟合的分流量变化曲线Fig.2.Variations of fractional flow in four oil reservoirs in China(exponential fitting)

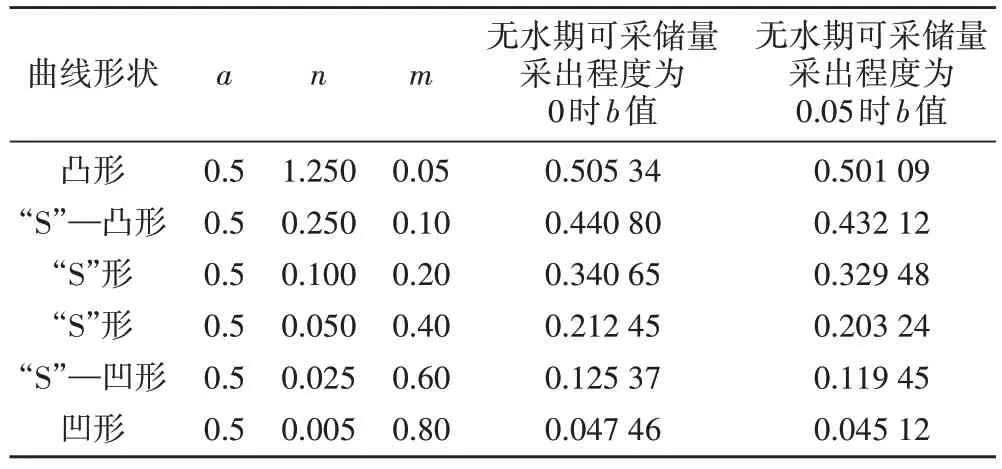
表4 典型含水变化曲线参数取值Table 4.Parameter values for typical water cut curves

由于（33）式中x含有2 个待定参数n和m，因此，采用双变量正交求解法，将文献［23］给出的5 类不同油藏可采地质储量采出程度与含水率生产数据代入（33）式，进行最优拟合，即先给定n的初始值为1，然后求得相关系数最大时的m值；再固定前面确定的m值，求得相关系数最大时的n值；重复前面2 个步骤，直至得到拟合相关系数最大时的n和m值，以及对应的a1、b1等待定参数（表5）。将拟合曲线与实际生产数据进行对比，拟合曲线与实际生产数据一致（图4），这也充分表明（8）式可以表征不同类型油藏的含水变化规律。

综上所述，所建的分流量解析方程（21）式，不仅可以描述岩心实验数据含水率与出口端含水饱和度的变化关系，而且其对应的（8）式也可描述油藏不同的采出程度和含水变化规律。

5 实例应用

巴喀油田西山窑组油藏属低孔特低渗裂缝型砂岩油藏，油层平均孔隙度为8.9%，平均空气渗透率为0.41 mD；地层原油密度为0.738 g/cm3，地层原油黏度为1.274 mPa·s，原始原油体积系数为1.255 3，气油比为113.5 m3/t，地层水黏度为3.46 mPa·s。巴喀油田西山窑组油藏于1996年6月投入注水开发，目前已进入高含水期低速开采阶段，但采出程度较低，仅为10%左右。

令y=Np，x=-（Wp+nNp+C）-m，那么，（5）式转化为一元一次线性方程y=A+Bx，将历年开发数据代入线性方程进行最优拟合，即采用多变量正交求解法（n、m、C），先固定C=0，n=1，求得最优m值；然后固定m值和C=0，求得最优n值；最后，固定m值和n值，求得最优C值。重复前面步骤，直到获得最大相关系数时的水驱特征曲线（图5a）；其次，反演得到含水变化规律（图5b）；最后，得到巴喀油田西山窑组油藏实际生产数据反馈的油藏渗流特征方程（图6）。

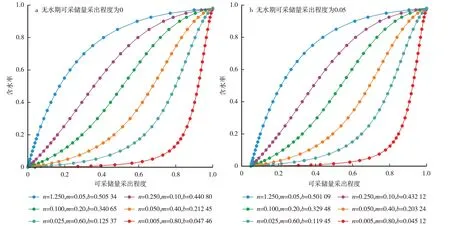
图3 广义含水变化规律曲线形态Fig.3.Generalized water cut variation curves

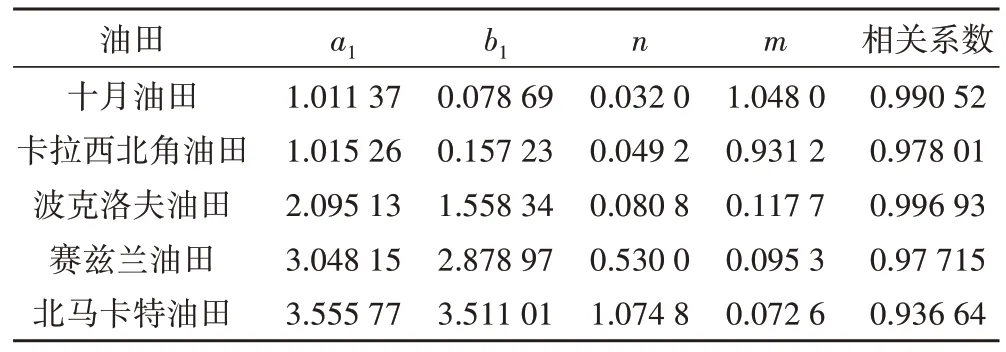
表5 文献［23］的5种不同油田含水规律拟合结果Table 5.Fitting results of water cut variations in five different oil fields mentioned in Ref.[23]

将油藏实际生产反映的渗流特征与水驱油实验未含裂缝的均质岩心得到的含水率与出口端含水饱和度关系曲线相比，差异非常明显。除非均质影响外，实际生产数据反映的是基质砂岩和裂缝共同对水驱油渗流特征的影响[24-25]，且单层油井实际生产结果也反映出油井一旦见水，迅速进入特高含水期的裂缝型油藏见水特征，表明巴喀油田西山窑组油藏裂缝对水驱油渗流特征影响较大。

6 结论

（1）本文提出的广义水驱特征曲线，在n取0 或1时可简化为俞启泰或卡扎科夫水驱特征曲线。

（2）广义水驱特征曲线对应采出程度与含水变化规律不仅可以有效描述无水期为0 或不为0 时凸形、“S”形、凹形含水变化规律，而且也能很好地拟合5 种开发过程较全的不同形态含水变化规律，适应性较强。

（3）利用Welge 方程，导出了水驱油微观渗流特征方程——新型分流量解析方程，该方程在特定条件下，可得到艾富罗斯实验结果，表明艾富罗斯实验结果只是文中水驱油微观渗流特征方程的一个特例。

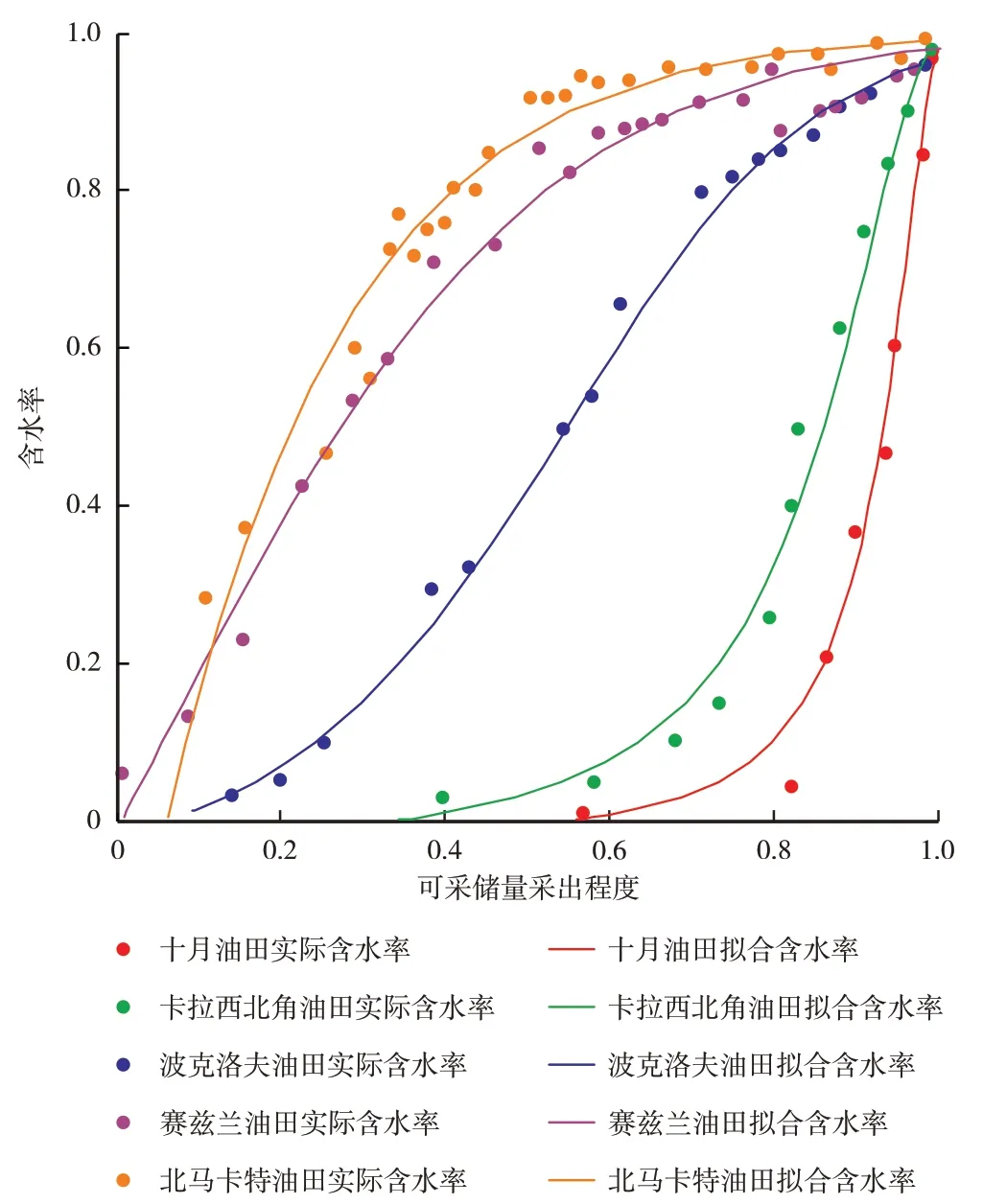
图4 文献［23］的5种驱替特征曲线Fig.4.Five characteristic curves of the oilfields mentioned in Ref.[23]

（4）通过中国4 个油田实例验证，本文提出的分流量解析方程与传统解析方程相比，拟合精度较高。

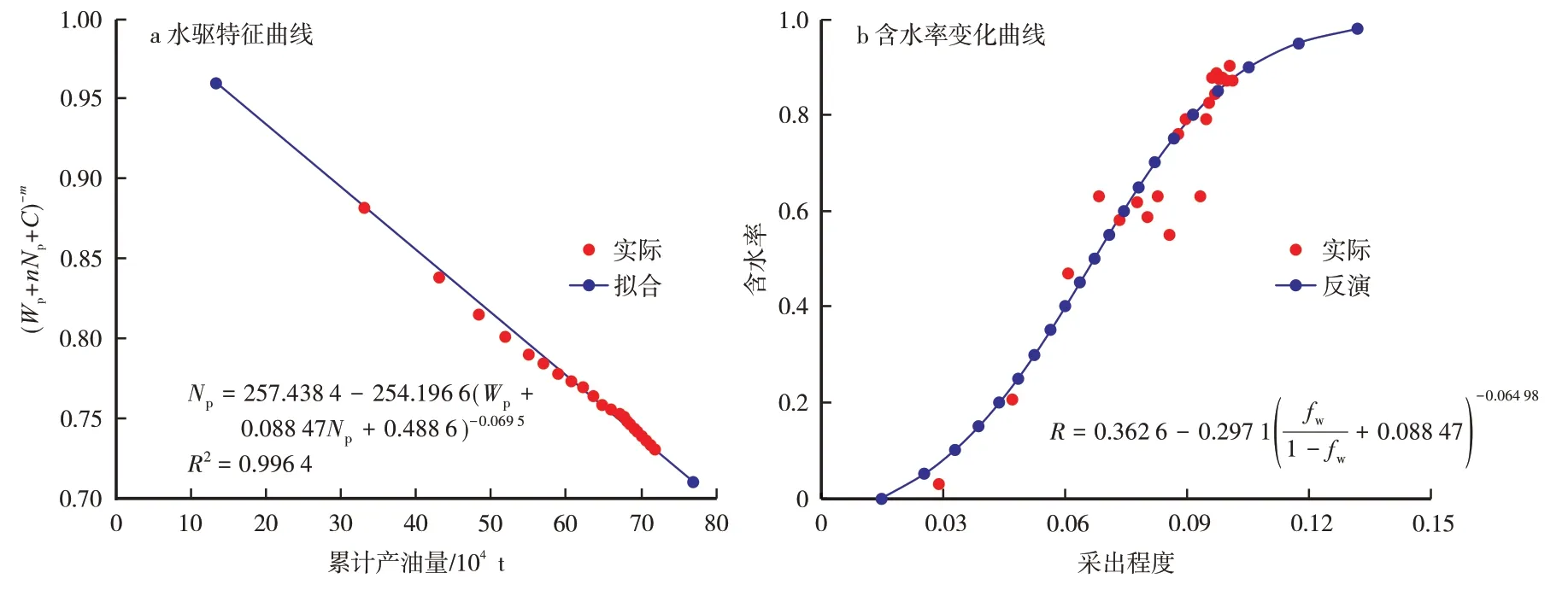
图5 巴喀油田西山窑组油藏水驱曲线Fig.5.Water flooding curves of the reservoir in Xishanyao formation in Baka oilfield

（5）利用反向推理技术，通过水驱特征曲线→含水变化规律→水驱油特征，可以确定油藏实际水驱油渗流特征。

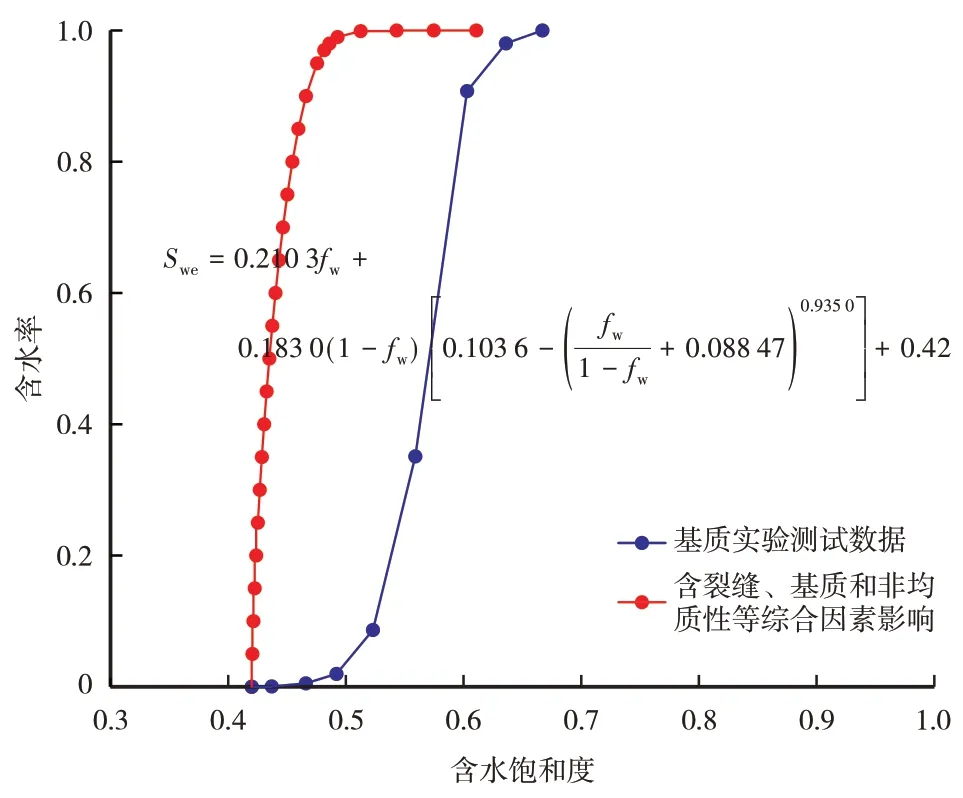
图6 巴喀油田西山窑组油藏含水率与含水饱和度曲线Fig.6.Water saturation vs.water cut of the reservoir in Xishanyao formation in Baka oilfield

符号注释

a，a1，A，b，b1，B，C，k，m，m0，n，n0——待定参数；

foe——出口端含油率，f；

fw——含水率，f；

Kro——油相相对渗透率，无量纲；

Krw——水相相对渗透率，无量纲；

Lp——累计产液量，104t；

N——地质储量，104t；

Np——累计产油量，104t；

qo——阶段产油量，104t/a或104t/月；

qw——阶段产水量，104t/a或104t/月；

R——采出程度，f；

RD——可采储量采出程度，f；

Sor——残余油饱和度，f；

Swe——出口端含水饱和度,f；

Swi——束缚水饱和度，f；

t——生产时间，a或月；

Wp——累计产水量，104t；

μo——地层原油黏度，mPa·s；

μw——地层水黏度，mPa·s；

μr——油水黏度比，f。