经典测量理论与项目反应理论的对比研究
胡恒潇,董航远
(西安思源学院教育学院,陕西 西安 710038)
1.引言
教育测量与评价是提升教育质量的有效手段。随着社会对教育质量的关注度越来越高,教育质量的评价方法也变得多样化。根据《国家中期教育改革和规划纲要2010-2020年》,不仅要改善教育课程的质量,还要强调教育课程测量和评价的效果方法。学业成就测试是检查教学质量的主要手段,不仅可以巩固课堂所教授的内容,检验教学是否有效,促进教师改进教学方法,提升教学质量。同时,为以后考试题目的修改与筛选和试题库的建立提供基础。目前,教育测量理论中常用的理论有经典测量理论(Classical Test Theory)和项目反应理论(Item Response Theory)。
2.经典测量理论(Classical Test Theory,CTT)
经典测量理论(Classical Test Theory, CTT)始于19世纪末,于20世纪30年代形成较为完整的体系。由于其模型简单,容易操作,至今为止在测量领域被广泛应用。在经典测量理论中,观察分数假设为真分数和误差分数,其模型如下所示:
X=T+E
X:观察分数
T:真分数
E:误差
2.1 基本假设
第一,如果某被试者的分数是90分,与其说该分数是学生的真正能力,不如说是被观察到的,即被测量的分数。该被测量的分数是指,未知的真正能力分数和测试过程中可能出现的误差分数构成
第三,观察分数是真分数和误差分数之和。
2.2 难度(Item Difficulty)
难度是题目的难易程度,也称难度系数(P),指在全体测试者中回答正确的测试者比率,即正确答案的概率。一般情况下,同样的试题,大部分测试者都能答对,此试题的难度较小。难度系数越大,就意味试题越简单。在计算试题的难度,应分为客观题难度的计算和主观题难度的计算。具体公式如下所示:

P:难度
N:总被试数
R:答对人数
在计算完每道题的难度后,可以通过对每部分题目的难度加权平均得出整套题的难度系数。确定了难度系数后,需要考虑测试的目的,如果是选拔性考试,难度系数值可较小,如果是学业测试,难度系数可较大。目前没有绝对的难度评价标准,各学者都有提出各自的评价标准。本研究使用了Cangelosi(1990)提出的题目难度评价标准,难度系数为0.25以下,题目困难;0.25-0.75,难度适中;0.75以上,题目简单。
2.3 区分度
区分度是指具体试题把不同水平的人区分开的程度,即题目的鉴别力。如,能力高的学生在各题中答对正确答案的比率要比能力低的学生答对正确答案的比率高。如果差异较少或没有差异,那么这道题目的区分度较低或没有区分度。区分度越高,越能区分出不同水平的学生,此题的价值也就越大。根据测验及题目的计分方式不同,一般情况下可以用下列公式来求得:一是点双列相关系数法,求考生总分与答对率之间的相关性。该方法适用于正确答案为1,错误答案为0,且考试总分为连续变量(如100分制的考试,89、91、98为连续变量)的情况。二是双列相关系数法。双列相关系数值反映了考生总分与答对率之间的相关性。双柱相关系数比判别指数更准确,所以在大规模考试中,一般用它来表现试题的判别性。测量学家Ebel(1965)提出了题目难度评价标准,区分度值在0.4以上,区分度优良;0.3-0.39,区分度合格;0.2-0.29区分度较低,需修改;0.19以下,没有区分度要淘汰。
3.项目反应理论(Item Response Theory,IRT)
项目反应理论,IRT)是教育测量领域的另一个代表性理论。它由瑟斯顿(1925)提出,由洛德和伯恩鲍姆发展而来,洛德和诺维克(1968)的经典教科书被认为是心理测量方法的里程碑。项目反应理论以数理统计理论为基础,采用非线性概率形式构建反应的概率模型。在此前提下,根据不同能力水平考生可能和实际的正确答案,构建相应的数学模型,运用统计技术控制实验误差。从试题入手,将试题对测量的影响参数化,从而准确估计被试的能力。
3.1 基本假设
项目反应理论是建立在强假设的基础之上。首先是能力单维性假设(unidimensionality)。所谓能力单维性假设是指,在测量试题时所有试题测量的必须是被试的同一种能力。同时需要满足局部独立性假设(local independence)。局部独立性假设是指试题之间对被试的影响相互独立互不干扰,被试之间的答对率也是相互独立互不干扰。
3.2 项目特征曲线(Item Characteristic Curve: ICC)
项目特征曲线是用来衡量被试对某个项目能够做出正确反应的概率的曲线。影响项目特征曲线的因素不仅包括项目的参数,还包括被试的潜在特征。项目特征曲线的X轴代表被试的能力水平,Y轴是答对答案的概率,被试的水平与题目本身拟合得较好的项目特征曲线的形状为S型。
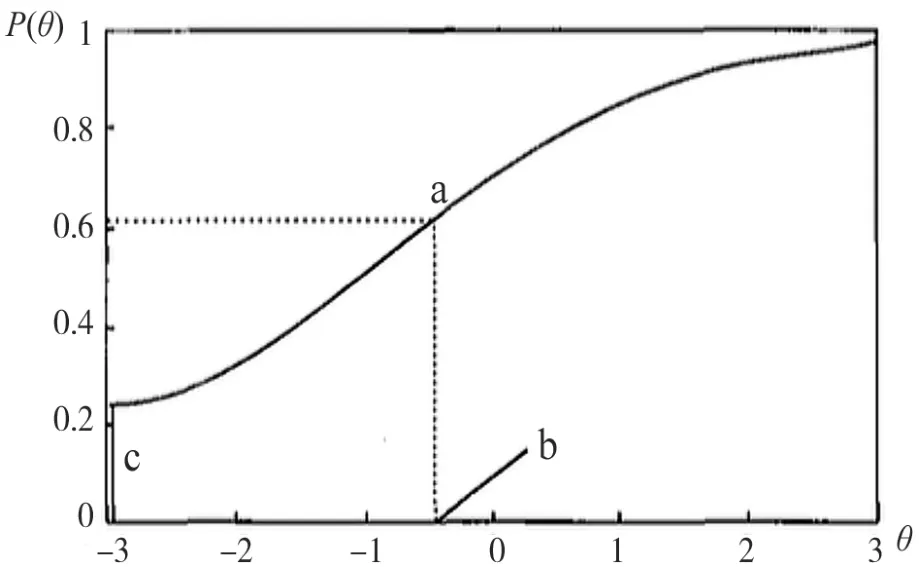
项目反应理论有多种数学最广泛的一个模型,因参数的不同可以分为单参数Logistic模型(又称Rasch模型)、双参数Logistic模型和三参数Logistic模型。三参数Logistic模型主要由难度、区分度、猜测度构成其项模型,通常通过这些模型对项目的特征进行描述。Logistic是使用目特征曲线。如图1所示:a:区分度;b:难度;c:猜测度;θ:能力。
3.3 难度、区分度、猜测度
区分度:如图1所示,拐点处的斜率a,代表测验项目的区分度,其值越大,说明区分度越高。韩国教授(2009)提出了题目区分度评价标准,在logistics模型中,区分度为0.00-0.34,无区分度;0.35-0.54,区分度低;0.65-1.34,区分度适中;1.35-1.69,区分度高;1.70以上,区分度非常高;+∞区分度完美。
难度:如图1所示,拐点处所对应的θ(拐点在横轴的投影)代表测验项目的难度b,其值越大,说明难度越大。韩国教授(2009)提出了题目难度评价标准,难度系数在-0.2以下,非常简单;-0.2--0.5,简单;-0.5-0.5,难度适中;0.5-2.0,题目困难;2.0以上,题目非常困难。
猜测度:图中特征曲线的截距c,表示项目的猜测指数。题目的推测指数是指,完全不具备能力的被试答对题目的概率。题目的推测指数越高,代表题目质量不佳,区分度越低。
4.经典测量理论与项目反应理论的对比

经典测量理论CTT 项目反应理论IRT模型 线性 非线性与样本关系 项目参数依赖于样本 项目参数独立于样本样本大小 200-500 根据模型而变化,一般500以上能力指标 总分 能力参数测量精度 信度估计 能力参数难度 答对人数/总人数 项目特征曲线(ICC)中0.5对应的能力区分度 总分与项目分数的相关关系 项目特征曲线(ICC)中项目难度的斜率
经典测量理论和项目反应理论是教育测量理论中的两个重要理论。经典测量理论的模型简单,容易操作,对于小规模的测试,利用经典测量理论进行教育测量是十分实用的。作为一种传统方法,它已经发展得比较完善,但仍有一些局限性:如采用的质量指标严重依赖样本;信度估计精度不高;参数指标之间配套性较差。项目反应理论克服了经典测量理论在教育测量技术上的困境,将被试特质与其在项目上的反应联系起来,具有项目参数独立于样本;被试与试题在同一量表之中;通过信息函数估计测量误差等优势,但由于测试条件要求严格,样本数量过大,被试范围要广,操作复杂等局限,因此,两种测量理论各有利弊,随着教育测量理论的发展,这两种理论也将不断得到完善。在不同的评价目的、评价对象、评价条件下,选择适当的教育测量理论,以获得更加有效全面的信息,促进教育质量的提升。

