Starship新型舵面形式气动特性数值模拟
张宇佳,左光,*,徐艺哲,杜若凡,赵飞,屈峰
1.中国空间技术研究院 载人航天总体部,北京 100094 2.西北工业大学 航空学院,西安 710072
自1961年加加林首次进入太空以来[1],人类的载人航天历史已经持续了50多年。经过探索,共发展了两类可以执行天地往返任务的载人航天器:美国的航天飞机[2]和以俄罗斯“联盟”号、中国“神舟”号为代表的载人飞船[3-4]。Mowry等[5]指出,在发展形成这两类载人航天器之后,载人航天运输工具天地往返方式便鲜有颠覆性的变化。载人飞船不可重复使用,而航天飞机只有少部分可重复使用,且维护成本高昂,因此天地往返运输成本一直居高不下[6],从而大大限制了天地往返运输的频率,阻碍了人类向更远的天空边界探索的步伐[7-8]。
近年来,民间商用航天力量的兴起为航天领域注入了新的活力[9-11],而其中的佼佼者就是SpaceX公司[12]。SpaceX公司通过采用栅格翼和矢量推力控制技术,实现了第一级火箭和助推器的回收降落与重复发射[13-17],从而大大降低了发射成本,将近地轨道的发射成本从航天飞机的$54 500/kg降低至$2 720/kg[18]。在回收火箭取得成功的基础上,SpaceX公司开始着手研制新型天地往返运输系统,并将其命名为Starship[12]。Starship与一级火箭助推器采用串联布置,设计总高度达130 m,起飞重量5 000 t,起飞推力达9 000 t, 一旦研发成功,其运载能力将远远超过现役各型火箭,代表天地往返运输系统的最前沿。同时,通过对一级火箭和Starship的重复使用,其载人天地往返运输成本可以大大降低,从而使载人航天走向常态化。
不同于传统载人飞船半弹道式再入大气层后通过降落伞回收,也不同于航天飞机在机场水平降落,Starship采用的降落方式更像其“猎鹰”火箭的回收降落方式[19],即通过舵面和矢量推力共同控制实现垂直降落。针对这一特殊的起降模式,Starship采用了不同于传统升力体飞行器的新型舵面控制方式。传统的升力体飞行器采用副翼、垂直尾翼和水平尾翼来实现姿态和航迹控制[20],而Starship则采用了前后两组可沿轴线方向偏转的翼面来实现对机体的控制。在再入返回阶段,Starship可以通过舵面的非对称偏转实现滚转姿态的调整,并通过侧向力的变化实现“倾侧”飞行,该种飞行模式可以使左右船体及舵面轮流迎风飞行,从而防止船体或舵面某一部分长时间在严酷的气动热载荷下飞行,降低防隔热需求。同时,舵面可以向船体方向收起,从而降低翼面的气动热载荷[21];在再入返回末段,其可以通过舵面控制实现船头仰起,并进入着陆准备阶段,之后通过舵面与矢量推力的组合控制实现垂直降落。
本文将主要聚焦Starship在再入返回末段和进入着陆准备后舵面的控制特性,由于Starship采用了新型的舵面控制方式,因此相对于传统升力体飞行器,其舵面控制率将会存在很大差别。目前对于该种舵面控制形式的研究非常有限,而舵面控制率将会直接影响其降落的安全性,尤其是在最后着陆阶段的安全性。因此,本文针对Starship的着陆阶段,采用数值方法对Starship不同舵偏下的气动特性进行研究,得到了舵面偏转对船体升阻力和三轴力矩的影响。
1 物理模型与数值方法
1.1 物理模型
Starship飞行器是针对天地往返和行星际旅行而设计的一种可重复使用运载器。SpaceX公司根据自身在可重复使用一级火箭上的技术积累和匹配性提出了该方案,如图1所示[22]。起飞时,其作为第二级运载器与“猎鹰”超级重型火箭串联垂直发射,降落时其采用与一级火箭相同的垂直降落方式。通过该种方案,Starship飞行器与一级火箭实现了最大程度上的技术通用性,从而大大降低了研制风险和运行成本。

图1 Starship与“猎鹰”超级重型火箭 [22]Fig.1 Starship and Falcon superheavy rocket [22]
目前,针对天地往返运输的一级重复使用运载器主要有3种方案:水平起降的一级载机方案,美国空军提出的垂直起飞水平降落的RBS方案[21](图2),以及SpaceX公司的垂直起降可重复使用火箭方案。水平起降的一级载机方案技术难度较高,目前仍在概念设计阶段。RBS方案采用并联形式,连接方式类似于航天飞机,该方案飞行阻力大,且并联方式分离时发生碰撞的可能性较高,危险系数更大。不同于前两个方案,Starship采用一二级串联形式,该种布置方式气动阻力小,且一二级分离危险系数低。同时,可重复使用火箭方案是目前唯一实现商业化运行的方案。通过多次成功的发射和回收,SpaceX公司在该领域已经积累了大量的经验。因此,从短期可行性和降低研发成本和系统风险等方面考量,一级可重复使用火箭都具有巨大的优势。鉴于以上原因,SpaceX公司最终选择该种一级二级布置方案。
由于Starship与一级火箭串联,因此其气动外形主体基本上属于轴对称形式,直径与“猎鹰”超级重型火箭相同,从而保证了气动外形的光滑连接,为减小气动阻力,头部为圆锥形。为实现姿态和轨迹的控制,其采用了前后两对全动舵面,该舵面可沿飞行器轴线方向转动,在飞行器再入时,可向船身两侧收起,从而大大降低舵面表面和前缘的气动热载荷。图3展示了本文对Starship精细化的气动热Qw仿真结果(仿真工况为80 km,Ma=15,此工况点为轨道再入升力体式飞行器再入时计算热流的一个典型工况),前后翼下表面前缘的气动热载荷均非常严酷。在此基础上,本文通过流线追踪法和经过形状因子以及压缩因子修正的参考焓方法对前后翼面偏转与展开时的表面热流进行了计算[23],如图4所示,翼面偏转后,前后翼的下表面热流均大幅度降低。

图2 可重复使用助推器与Ariane 5火箭[21]Fig.2 Two attached reusable fly-back boosters from Ariane 5 core stage[21]

图3 Starship在80 km、Ma=15时的气动热仿真Fig.3 Aerodynamic thermal simulation of Starship at 80 km and Ma=15

图4 Starship在80 km、Ma=15翼面收起与展开时的表面热流对比Fig.4 Comparison of surface heat flux between deflected wing and deployed wing of Starship at 80 km and Ma=15
目前,传统升力体式可重复使用的天地往返运输系统基本思路仍属于继承航天飞机的思路,气动布局和飞行控制方式仍是结合飞机的控制方式,而Starship新的气动布局和气动操纵方式为未来天地往返飞行器提供了新的思路。
本文根据SpaceX官方网站公布的尺寸参数[22],对Starship进行了三维建模,如图5所示,整个船体长50 m,直径9 m,后翼展长18 m,前翼展长15 m。整船重1.0×105kg,船体采用不锈钢制造,根据船体外形以及内部燃料储箱和发动机的布置情况,估算得到整船重心距机头40 m,通过重心的俯仰轴惯量矩为3.7×107kg·m2。

图5 Starship三维模型Fig.5 Starship 3D model
Starship采用的是垂直起飞入轨,水平再入并垂直降落的飞行模式,因此在低速阶段,其主要进行的是大攻角飞行并最终实现垂直降落。针对这一飞行模式,本文分别选取了60°攻角和120°攻角(进入着陆准备后,船头仰起,攻角将大于90°)下不同舵偏的工况进行研究。值得注意的是,在大攻角下,Starship这样的类旋成体飞行器,其流场必然存在大分离现象,具有非常强的非定常特性,因此其舵面控制率也必然存在很强的非线性,这对于研究此舵面形式的舵面控制率较为不利。鉴于此,本文增加了5°攻角下不同舵偏工况的研究,通过对小攻角下不同舵偏工况的数值模拟,能够对该种舵面布置形式的气动特性有一个更加系统性的认知。计算工况如表1所示。前后翼舵偏均为0°~60°,而在60°攻角时,考虑到大分离情况下左右两侧翼面可能存在非对称性,故对单侧偏转和双侧同时偏转的工况均进行了模拟。在此基础上,本文通过采用整体动网格方法,对Starship的非定常俯仰运动进行了数值模拟。该方法不需要网格重构,通过运动边界实现动网格计算。因此,相比于传统的网格重构方法,该方法可以将计算效率提高一个量级,实现了对Starship舵面在大攻角降落时的非定常流场中俯仰通道上舵效的快速有效评估。

表1 计算工况Table 1 Computation cases
1.2 数值方法
通过采用有限体积法来求解三维不可压Navier-Stokes方程。控制方程包括连续性方程和动量方程:
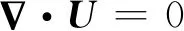
(1)
(2)

数值模拟采用非结构网格,并在船体表面生成棱柱体边界层网格,网格总量1 400万,船身表面网格及边界层网格如图6所示。船体表面采用壁面边界条件,远场采用Opening边界条件,气流可以在该边界上流入和流出。计算采用全湍流模拟,湍流模型选取k-ωSST两方程模型。

图6 Starship表面网格及边界层网格Fig.6 Surface and boundary layer mesh of Starship
2 计算验证
选取NASA在第一届AIAA高升力大会发布的TrapWing模型的实验数据[24]以及Wang等[25]对该模型的数值模拟结果进行对比以验证本文数值方法的准确性,实验模型如图7所示。该模型的平均气动弦长c=1 m,模型半展长2.16 m,参考面积2.05 m2。前缘缝翼和后缘襟翼分别偏转30°和25°,前缘缝宽和高均为0.015c,后缘缝高和重叠部分分别为0.015c和0.005c。来流马赫数Ma=0.2,雷诺数Re=4.3×106。

图7 NASA TrapWing 模型及本文生成的机体表面网格Fig.7 NASA TrapWing geometry and surface mesh of the proposed method
图8展示了本文计算得到的升、阻力系数(CL和CD)与实验[24]以及Wang等[25]计算结果的对比。本文计算结果与实验结果吻合很好,在中小攻角时,本文计算结果要优于Wang等的计算结果;在大攻角情况下,计算结果与实验值存在一定的偏差,但差值仍小于3%。因此本文选取的计算方法可以满足计算精度的要求。


图8 本文计算得到的NASA TrapWing的升、阻力系数与实验[24]以及Wang等[25]计算结果对比Fig.8 Comparisons between calculated lift and drag coefficients of NASA TrapWing in this paper and those by Wang et al. [25] as well as experiment[24]
3 结果与讨论
3.1 Starship大攻角下气动特性
图9对称面流线展示了5°和60°攻角无舵偏情况下,船体对称面流线分布,流线上的颜色云图为速度云图,船体表面云图为压力云图。图10展示了这两个工况沿X方向一系列截面上的涡量云图。由图9的流线分布可知,在5°攻角时,流场基本贴体,仅在船体尾部存在一个分离区,船体前缘驻点靠近船体前缘点,在头锥部分,由于流道收缩,存在很明显的加速减压效应;在60°攻角时,船体背风面基本分离,前缘驻点明显下移,船体表面压力分布主要受涡系结构影响。
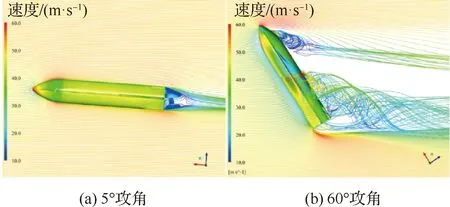
图9 对称面流线Fig.9 Streamlines starting from symmetry plane

图10 Starship船体背风面涡量云图Fig.10 Vorticity contour in leeward side of Starship
图10清晰地展示了船体背风面的涡结构,在5°攻角时,主要有4组涡系结构,包括涡系a(前翼前缘涡)、涡系b(前翼内侧产生的涡)、涡系c(两侧边条涡)以及涡系d(后翼前缘涡)。这4组涡系结构相对稳定,并逐渐向下游发展。而在60°攻角时,在上述4组涡系的基础上增加了一对由船体头部前缘产生的涡系结构e,并且机体左右两侧涡系不对称性非常明显,随着涡系向下游发展,各涡系之间会逐渐发生融合,特别是涡系b、c、d之间的融合异常显著。这种涡系结构的非对称性必然会造成表面压力分布的非对称性,如图11 所示,船体的下表面左右压力分布较为对称,而船体上表面的压力分布则存在明显的非对称性。这种强的非对称特性会对舵面的控制特性带来非常显著的影响。

图11 60°攻角时船体上下表面压力云图Fig.11 Pressure contour on Starship upper and lower surface at 60° of angle of attack
3.2 Starship舵面控制率
Starship采用的舵面控制方式如图12所示,其可以分别通过前翼的单侧和双侧偏转、后翼的单侧和双侧偏转以及前后翼的组合偏转来实现飞行器俯仰、偏航以及滚转三轴的控制。该种舵面控制形式与图13中基于副翼以及尾翼的舵面控制形式存在很大的不同,下文将对该种新型舵面控制形式的控制率进一步研究,定义舵面向上偏转为正。

图12 Starship所采用的舵面控制方式Fig.12 Control surface model of Starship
图14展示了5°攻角下升力系数和阻力系数随舵偏角的变化。后翼偏转对升力系数的影响较为显著,随着后翼偏转角度的增加,升力系数单调减小,偏转角度与升力系数基本成线性关系。由此可见后翼作为主升力面,其偏转对升力影响较大。前翼偏转则对阻力系数的影响较为显著,随着前翼偏转角度的增加,阻力系数增加,偏转角度与阻力系数基本线性相关。其主要原因为前翼旋转轴并非与机体轴平行,因此其偏转后会增加迎风面积,从而增加阻力。同时值得注意的是,在前翼偏转后会引起升力系数的增加,当其偏角小于40°时,升力系数与前翼偏角基本线性相关。

图13 传统襟副翼控制方式Fig.13 Control model through traditional flaperon
图15展示了5°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图。在舵面偏转以后,后翼前缘涡的强度明显降低,后翼上表面受前缘涡影响而形成的低压区减小,如图15(a)椭圆框中所示。因此,偏转一侧升力系数降低。同时,由于升力方向翼面有效面积的减小,会造成偏转一侧翼面升力的减小。综合上述两个原因,后翼升力系数将随着偏转角度的增加而单调减小。


图14 5°攻角下升力系数和阻力系数随舵偏角变化Fig.14 Variations of lift coefficients and drag coefficients with wings deflection angle at 5° angle of attack
图16展示了侧向力系数CY和三轴力矩系数(Cmx,Cmy,Cmz)随舵偏角的变化,其中取矩点为机头位置。前翼与后翼偏转对于侧向力的影响非常接近,当偏转角小于40°时,侧向力系数随着偏转角的增加单调减小,两者近似线性相关。对比图16与图14可知,后翼偏转引起的侧向力与阻力的变化相较于升力要小一个量级,因此滚转力矩系数和俯仰力矩系数的变化主要由后翼偏转造成的升力变化引起,其变化趋势与后翼升力系数的变化趋势非常接近,如图16(b)和图16(c)所示。后翼偏转角与滚转力矩系数和俯仰力矩系数均存在较好的线性相关性。前翼偏转对俯仰力矩系数影响较小,对滚转力矩系数几乎无影响。而偏航力矩系数则主要由侧向力的变化引起,当偏转角度小于40°时,偏航力矩系数与前翼或者后翼的偏转角基本线性相关,且前翼的舵效约为后翼的40%。

图15 5°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图Fig.15 Pressure contour on surface and vorticity contour in leeward side of Starship with one side rear wing deflecting 60° at 5° angle of attack
在确定了舵面偏转与三轴力和力矩的关系之后,便可以确定Starship的三轴控制方式。因为后翼偏转角与俯仰力矩系数的线性相关性较好,所以可以通过双侧后翼的对称偏转实现俯仰方向的控制;前翼在偏转角小于20°时,偏转角与俯仰力矩系数相关性较好,因此双侧前翼可以通过微幅偏转实现俯仰方向的精确控制。前翼的偏转对偏航力矩系数的影响非常显著,同时滚转力矩系数和俯仰力矩系数的耦合变化则较小,所以通过双侧前翼的非对称偏转可以实现偏航方向的控制。后翼偏转角与滚转力矩系数线性较好,可以用于控制滚转运动,但后翼的偏转同时还会耦合偏航力矩的变化,可以通过双侧后翼和前翼的组合偏转实现滚转方向的控制。Starship姿态的控制流程图如图17所示。
通过以上分析可知,Starship仅凭前后4个翼面的组合偏转即可实现三轴运动的控制。对于不需要大翼面积的飞行器,如再入飞行器,该种控制方式非常适合。
图18为60°攻角时新型舵面控制形式以及传统襟副翼控制方式下,升力系数和阻力系数随舵偏角度的变化,其中虚线和实线分别为新型舵面后翼单侧偏转和双侧偏转后升力系数变化的线性拟合。相比于5°攻角,升力系数以及阻力系数与舵偏角度的相关性明显下降,并且由于流场的不对称性,双侧偏转也并非单侧偏转的叠加。其中,前翼的偏转与升力系数和阻力系数的相关性非常弱。后翼单侧偏转与升阻力的相关性减弱,但其双侧偏转时,后翼偏转角与升力系数仍保持了非常好的线性相关性。无论是单侧偏转还是双侧偏转,新型舵面控制方式的舵偏角与升力系数的线性相关性均优于传统的襟副翼控制方式(图18中五角星标所示)。

图17 Starship姿态控制流程图Fig.17 Flow chart of Starship attitude control
图19展示了60°攻角时新型舵面控制形式以及传统襟副翼控制方式下,侧向力系数和三轴力矩系数随舵偏角度的变化,其中虚线和实线分别为单侧偏转和双侧偏转后升力系数变化的线性拟合。无论采用新型舵面控制形式还是传统襟副翼控制方式,侧向力系数和偏航力矩系数均随着舵偏角的增加在零点附近左右摆动,并不存在很强的相关性,如图19(a)和图19(d)所示,其值受涡系的摆动和脱落影响很大。对于新型舵面控制形式,滚转力矩系数和俯仰力矩系数与后翼偏转仍然存在较强的线性相关性,尤其是俯仰力矩系数受后翼偏转引起的升力变化的影响,在后翼双侧偏转时,其与偏转角近似线性相关。但是传统的襟副翼控制在大攻角下基本失效,俯仰力矩系数和滚转力矩系数与副翼偏角相关性并不强。因此,在60°攻角下,传统的襟副翼控制方式基本失效,而Starship仍可通过后翼两侧同时偏转实现俯仰控制。新型舵面控制方式在大攻角下的可控性是传统襟副翼控制方式所不具有的能力。

图18 60°攻角下升力系数和阻力系数随舵偏角变化Fig.18 Variations of lift coefficients and drag coefficients with wings deflection at 60° angle of attack
图20展示了60°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图。船体背风面左右两侧涡结构不对称性明显,使得船体背风面压力分布也存在明显的不对称性,尤其是两侧边条涡形成的低压区。随着左右两侧涡系的间歇性脱落,侧向力必然会产生波动,从而造成偏航力矩的波动。
在此攻角下,后翼前缘涡脱体,其形成的低压区消失,因此后翼偏转后上翼面压强差别并不明显。但是气流冲击后翼下表面所形成的高压显著增加,后翼的偏转对于下表面压强的影响较为显著。由于后翼偏转引起的后翼下表面压强的降低以及升力方向翼面有效面积的减小使得后翼的升力系数随着偏转角度的增加而近似线性减小,因此即使在船体背风面存在大的分离区,星船仍可通过后翼双侧的偏转实现俯仰方向的控制。

图19 60°攻角下侧向力系数与三轴力矩系数随舵偏角变化Fig.19 Variations of lateral force coefficients and three-axis torque coefficients with wings deflection at 60° angle of attack

图20 60°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图Fig.20 Pressure contour on surface and vorticity contour in leeward side of Starship with one side rear wing deflecting 60° at 60° angle of attack
在进入着陆准备后,船头仰起,攻角将大于90°,相对于船体来说,意味着来流方向反向,此时的流场将严重背离传统的襟副翼设计流态。而对于“星船”所采用的舵面形式来说,由于其沿飞行器轴线方向偏转,因此其控制模式不会发生根本性变化,只是舵面的前后缘发生了转换。图21展示了120°攻角时新型舵面控制形式升力系数和三轴力矩系数随舵偏角度的变化(取矩点为机头位置)。相比于60°攻角,此时舵面偏转与升力系数以及三轴力矩系数的相关性非常强。不仅在俯仰通道,在滚转通道和偏航通道其均能保持良好的操纵特性。因此,在“星船”着陆阶段其仍能通过舵面偏转对自身姿态进行有效控制,但是注意到舵面偏转将会耦合升力系数的变化,因此其还需通过矢量推力对自身轨迹进行控制。通过舵面和矢量推力的组合控制,“星船”将能在着陆阶段实现对自身姿态和轨迹的精确控制。

图21 120°攻角下升力系数与三轴力矩系数随舵偏角度变化Fig.21 Variations of lift coefficients and three-axis torque coefficients with wings deflection at 120° angle of attack
图22展示了120°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图。相比于60°攻角时,船体背风面的压力分布趋于左右对称,结合背风面涡结构云图可知,左右翼面的翼尖涡和边条产生的涡系相对独立,不存在明显的相互诱导和干扰,涡系结构相对稳定,背风面由边条涡形成的低压区大幅减弱。因此相比于60°攻角工况,“星船”舵面偏转与三轴力矩系数的相关性大大增强。即当来流攻角大于90°时,“星船”舵面的控制效能反而有所增强,这将有利于其降落时的精准控制。
3.3 Starship非定常俯仰运动模拟
鉴于60°攻角下,Starship仍可通过后翼偏转实现有效的俯仰运动控制,本文通过采用整体动网格方法对后翼双侧偏转60°情况下整船的非定常俯仰运动过程进行了数值模拟,旋转轴通过重心平行于Y轴。整个运动过程如图23所示,其中箭头表示船体对称平面上的速度矢量,云图代表速度的大小。图24展示了整个运动过程中俯仰角加速度、角速度以及俯仰角随时间的变化。

图22 120°攻角下后翼单侧偏转60°船体上下表面压力云图及船体背风面涡量云图Fig.22 Pressure contour on surface and vorticity contour in leeward side of Starship with one side rear wing deflecting 60° at 120° angle of attack

图23 后翼双侧60°舵偏时船体在气动力 作用下的俯仰运动过程Fig.23 Starship pitching motion under aerodynamic forces with both sides rear wing deflecting 60°

图24 Starship俯仰角加速度、角速度以 及俯仰角随时间变化Fig.24 Variations of pitching angular acceleration, angular velocity and angle of Starship with time
在后翼偏转以后,整船受到一个负力矩,逐渐进行抬头运动。同时,背风面的分离区逐步变大,俯仰角加速度的值单调减小,但是在t≤3 s时,角加速度一直保持负值,因此在此时间历程内,Starship一直在作角加速度逐步减小的加速旋转运动。在2.5 s内,整船的俯仰角变化接近45°。因此在降落阶段,Starship完全可以通过后翼的偏转来实现俯仰控制。
4 结 论
针对Starship的再入飞行和着陆阶段的飞行控制方式,对Starship新型舵面形式的气动特性进行了系统的研究,主要结论如下:
1) 星船舵面在小攻角和大攻角下均能实现对船体姿态的有效控制,其中后翼为主控制面。
2) 后翼偏转角与俯仰力矩系数的线性相关性较好,可以通过双侧后翼的对称偏转实现俯仰方向的控制;前翼的偏转对偏航力矩系数的影响显著,且与滚转力矩系数和俯仰力矩系数的耦合较小,可以通过双侧前翼的非对称偏转实现偏航方向的控制;后翼偏转角与滚转力矩系数线性较好,但后翼的偏转会耦合偏航力矩的变化,可以通过双侧后翼和前翼的组合偏转实现滚转方向的控制。
3) 在大攻角下,尤其是在着陆阶段攻角大于90°的情况下,传统的襟副翼控制方式失效可能性较大,而Starship新型舵面控制形式前翼和后翼偏转与三轴力矩系数的相关性仍非常强。其对于俯仰通道、滚转通道和偏航通道均能保持良好的操纵特性。
[21] SIPPEL M, MANFLETTI C, BURKHARDT H. Long-term/strategic scenario for reusable booster stages[J]. Acta Astronautica, 2006, 58(4):209-221.

