垂尾抖振响应的鲁棒-FxLMS主动控制试验
刘昊,王巍,金伟,牛文超,杨智春,*
1. 西北工业大学 航空学院,西安 710072 2. 成都飞机设计研究所,成都 610091
双垂尾布局是现代高性能战斗机普遍采用的一种构型,在大迎角机动飞行条件下,其机身前体或机翼后缘的分离涡产生的非定常气动载荷会作用在垂尾上,带来严重的气动弹性抖振问题[1]。国内外学者的研究表明利用压电作动器对垂尾抖振作振动压电主动控制是解决该问题的有效途径,美国、澳大利亚和加拿大研究人员发起的合作研究项目,深入地研究了使用主动控制技术降低F/A-18垂尾抖振的问题,建立了混合式抖振控制系统,使用舵结构控制垂尾的弯曲模态,使用安装在垂尾表面上的压电作动器控制垂尾的扭转模态,并设计了LQG(Linear Quadratic Gaussian)控制器[2];Chen等[3]考虑不同飞行状态下抖振控制系统的鲁棒性,开展垂尾抖振响应的鲁棒控制研究;国内,杨智春教授课题组[4-6]针对垂尾的抖振响应的压电主动控制问题开展了一系列控制方法研究,如主模态控制、LQG控制、鲁棒控制、分数阶正位置反馈(FOPPF)控制等,并进行了抖振控制的地面(模拟)试验及风洞试验。随着压电主动控制技术的成熟,控制系统性能提升成为了垂尾抖振响应主动控制的研究热点,要求设计的控制器具有更优的控制性能、更高的鲁棒性。
本文开展垂尾抖振响应的鲁棒自适应振动主动控制研究。在自适应振动主动控制系统中,通常采用有限脉冲响应(Finite Impulse Response, FIR)滤波器作为自适应控制器,控制器参数的更新基于最小二乘(Least Mean Square, LMS)算法,称为FxLMS控制算法[7]。对算法中次级通道的改进是一种改善其控制性能的有效途径。Ardekani和Abdulla[8]的研究表明,适当调整次级通道辨识模型的设计参数,可以提高FxLMS算法的收敛速度;李嘉全和王永[9]验证了增加次级通道的阻尼可以提高FxLMS算法的性能,还提出了一种前馈阻尼补偿的FxLMS算法[10]。
鲁棒控制是一种解决控制对象模型和外界扰动具有不确定性的控制方法,现代鲁棒控制方法主要以H∞控制方法[11]、结构奇异值μ方法[12]等为主。鲁棒控制自提出以来,经过30多年的研究和发展,已经具备成熟的理论,并得到广泛的应用。在航空航天领域,很好地解决了各种结构的振动主动控制问题,如直升机振动响应的控制问题[13]、垂尾抖振的控制问题[14]以及机翼颤振的控制问题[15]等。
针对飞机垂尾抖振响应控制对高控制性能和高鲁棒性的要求,本文基于次级通道阻尼补偿理论,提出了设计鲁棒控制器对次级通道进行反馈式阻尼补偿的鲁棒-FxLMS控制算法(后面简称为RFxLMS控制算法),并设计出相应的RFxLMS控制器。采用MFC(Macro Fiber Composite)压电作动器,开展垂尾抖振响应主动控制的地面模拟试验,验证了本文所提出的RFxLMS控制器的控制性能优于鲁棒控制器和FxLMS控制器的控制性能。最后通过垂尾模型抖振响应的主动控制风洞试验,验证了控制器对垂尾抖振响应控制的有效性。
1 鲁棒-FxLMS主动控制算法
1.1 反馈式次级通道阻尼补偿方法
FxLMS控制算法的性能受步长因子的直接影响。用Λ表示保证FxLMS控制算法稳定的步长因子取值上限,FxLMS控制算法的稳定性和收敛速度是Λ的单调增函数[16]。
步长因子取值的上限Λ与FxLMS控制算法中的次级通道(即振动主动控制中的被控对象)存在如下正相关关系[9]:
(1)
式中:G(s)为次级通道的传递函数模型。
式(1)表明次级通道的动力学特性会影响FxLMS控制算法的性能。然而次级通道特性是由物理系统决定并无法改变的,为了改善次级通道动力学特性,提高FxLMS控制算法的性能,李嘉全等[10]提出了一种前馈式等效阻尼补偿方法,在FxLMS控制算法的框图中次级通道G(s)的前面增加一个自适应前馈阻尼补偿器F(s),构成阻尼补偿次级通道模型C(s),原理如图1(a)所示。灵敏度反映一个系统的状态或输出变化对系统参数或周围条件变化的敏感程度。前馈式阻尼补偿次级通道是一个开环系统,理论上开环系统的灵敏度为1,对于摄动的作用毫无抑制的能力。
系统灵敏度定义为系统传递函数的变化率与被控过程传递函数变化率的比值。闭环系统C(s)关于G(s)的灵敏度SG(s)表示为
(2)
设计控制器的目标是降低开环系统的灵敏度,在设计范围内的K(s)G(s)通常较大,进一步可以得到:

(3)
式中:K(s)是针对次级通道设计的鲁棒控制器。结合式(1)及式(3)可知,对次级通道设计控制器组成闭环系统,可以起到反馈式阻尼补偿的效果,进而提高FxLMS控制算法的稳定性和收敛速度。
由于闭环系统可以有效降低原系统的灵敏度,本文提出将次级通道G(s)与控制器K(s)组成闭环子系统C(s),来实现次级通道的反馈式阻尼补偿,原理如图1(b)所示。其中,控制器的反馈信号根据式(7)所示的解耦方法得到。

图1 两种阻尼补偿方法对比Fig.1 Comparison of two damping compensation methods
1.2 鲁棒-FxLMS控制算法

图2 RFxLMS控制算法结构图Fig.2 Block diagram of RFxLMS control algorithm
本文提出的的鲁棒-FxLMS控制算法原理如图2所示,相较于经典FxLMS控制算法做了2点改进:① 经典FxLMS控制算法一般要求预知外激扰作为参考信号,但是在实际的结构振动主动控制中,外激扰信号难以预知和采集,故这里采用了式(6)所示的一种信号重构的方法来提供参考信号,具体做法是,采集垂尾结构振动响应信号进入构造过程,进而基于自适应控制器和次级通道辨识模型构造出参考信号,当次级通道的辨识模型足够精确时,构造的参考信号与外激扰信号的相关性较好,可以保证控制算法的收敛性和稳定性[17];② 采用1.1节提出的反馈式阻尼补偿方法,设计鲁棒控制器来对次级通道进行阻尼补偿。

(4)
W(z)为依据最小均方算法随误差实时更新权值的自适应控制器,同样为FIR滤波器形式,阶数为N,可以表示为
(5)
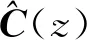
(6)

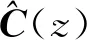
(7)
由式(6)和式(7)可知,eR(n)=x(n),鲁棒控制器的反馈误差信号与FxLMS控制器的参考信号相同。
参考信号重构的FxLMS算法迭代过程可概括为
(8)
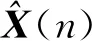
X(n)=[x(n),x(n-1),…,x(n-N+1)]T
算法步长因子μ满足收敛性要求的选取范围为
(9)
式中:λmax为滤波器输入参考信号的自相关矩阵的最大特征值。
实际情况下,外界环境因素的干扰会引起模型的参数摄动,使次级通道产生误差,当次级通道的辨识模型与实际模型的相位差大于90°时,会影响FxLMS控制算法的收敛性[18]。次级通道模型的参数摄动率ΔG(s)/G(s)与阻尼反馈补偿次级通道模型的参数摄动量ΔC(s)/C(s)满足如下关系式:
(10)
式(10)表明,外部干扰引起的次级通道模型的参数摄动为ΔG(s)的情况下,阻尼补偿次级通道模型的参数摄动率更小,由于辨识模型的误差较小,对控制算法收敛性的影响也更小。因此,RFxLMS控制算法相较于FxLMS控制算法具有更好的鲁棒性。
2 垂尾模型及垂尾抖振响应主动控制系统
2.1 垂尾模型
本文研究中使用的垂尾模型如图3所示。

图3 粘贴MFC压电作动器的垂尾模型Fig.3 Vertical tail model with pasted MFC piezoelectric actuator
垂尾模型的具体参数如下:
1) 垂尾模型的展长为0.23 m,有效面积为0.052 m2,翼剖面采用对称翼型。
2) 垂尾模型的内部结构是厚度为1 mm的铝合金板,在铝合金板的两面(A面和B面)对称贴有2片MFC压电作动器(M8557-P1型),粘贴在B面根部的压电作动器命名为M1b(图3),A面根部的压电作动器命名为M1a。MFC压电作动器的粘贴位置和角度经遗传算法优化得到,该布局方案对垂尾模型的前两阶模态响应均具受控制能力,压电作动器的布局优化方法采用文献[19] 提出的压电作动器连续布局优化方法。
3) 在垂尾模型梢部后缘装有一个加速度传感器(PCB 333B30型),用于测量垂尾模型的振动响应。
4) 垂尾模型的边界条件为根部固支,垂尾模型的根部通过夹具与底座连接,底座用螺栓固定在试验台面上。
2.2 垂尾抖振响应的主动控制地面试验系统
抖振控制器性能的优劣需要通过抖振主动控制试验的验证,风洞试验验证前需要经过地面试验验证并调试控制器。垂尾模型的抖振主动控制地面试验系统分为3个部分:
1) 试验模型:粘贴MFC压电作动器及加速度传感器的垂尾模型。
2) 激励系统:在QuaRC半实物仿真平台中搭建信号发生器模块产生激励信号,该信号经功率放大器(HVA 1500/50-4,Smart Material Cop.)放大后,驱动垂尾模型A面根部的压电作动器M1a,模拟抖振载荷对垂尾进行激励。
3) 主动控制系统:通过加速度传感器测量垂尾结构振动响应信号,经过信号调理器输入到QuaRC输入板卡,由搭建在Simulink中的控制器计算出控制信号,该信号通过功率放大器放大后驱动垂尾模型B面根部的压电作动器M1b,实现对垂尾结构的抖振主动控制。
垂尾模型的抖振响应主动控制地面验证试验系统如图4所示。

图4 垂尾抖振响应的主动控制地面验证试验系统Fig.4 Ground test system for vertical tail buffeting active control
2.3 垂尾抖振响应主动控制风洞试验系统
垂尾模型抖振响应主动控制的风洞试验系统如图5所示。垂尾模型安装在风洞试验段,在其上游安装一个可调迎角的厚翼型翼段(称为扰流翼段),作产生脱体涡激励的装置,调节扰流翼段到垂尾模型的距离,使得脱体涡到达垂尾模型前刚好破裂而形成产生抖振激励载荷的非定常扰流,给定风速下抖振载荷的强度通过改变扰流翼段的迎角来调节。为了提高压电作动器的控制输出能力,在垂尾模型抖振响应的风洞控制试验中使用了2组对位粘贴的MFC压电作动器,即给两面的压电作动器施加幅值相同、相位相反的控制电压信号,其余信号采集及控制仪器设备与垂尾模型抖振响应的地面(模拟)试验相同。

图5 垂尾抖振响应的主动控制风洞试验系统Fig.5 Wind tunnel test system for vertical tail buffeting active control
3 被控系统辨识与控制器设计
垂尾抖振响应通常以其结构的低阶模态响应为主。本节开展垂尾模型抖振被控系统的辨识和垂尾抖振响应控制器设计,为了对比显示本文提出的RFxLMS控制器的优势,针对垂尾模型的一阶弯曲模态响应和一阶扭转模态响应控制,同时也设计了多模态的FxLMS控制器和鲁棒控制器。
3.1 垂尾抖振响应被控系统的试验建模
垂尾抖振响应控制系统如图6所示,可分为垂尾结构子系统、作动器(包括功率放大器)/传感器(包括信号调理器)子系统和控制器子系统三部分;从功能的角度出发,又可以分为垂尾抖振被控系统(虚框内)和控制器(虚框外)两部分。
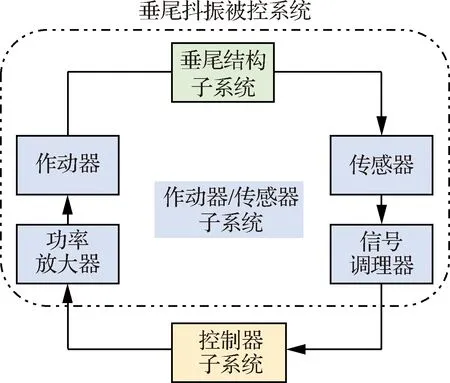
图6 垂尾抖振响应控制系统示意图Fig.6 Diagram of vertical tail buffeting control system
垂尾抖振被控系统的建模是垂尾抖振控制器设计的基础。考虑到本文垂尾抖振被控系统中不仅包括垂尾结构,而且包括压电作动器、传感器、信号调理器、功率放大器等机电元件和仪器,直接进行理论建模比较困难,同时考虑到控制器设计对垂尾抖振被控系统模型精度的要求,本文使用系统辨识的方法开展垂尾抖振被控系统的建模。
垂尾抖振响应被控系统的辨识数据采集基于图4搭建的试验系统。首先通过计算机产生带宽为0~45 Hz的窄带随机信号,通过高压功率放大器放大后,驱动垂尾模型B面的压电作动器M1b对垂尾模型结构进行激励;采用加速度传感器测量垂尾模型的振动响应,信号在经过加速度信号调理器后,由QuaRC采集,最终在计算机内使用设计带宽为0~45 Hz的8阶Butterworth带通数字滤波器对输出信号滤波,完成辨识数据的采集。辨识输入、输出信号的采集时长为40 s,采样率为1 000 Hz。
3.2 鲁棒控制器设计
本文采用结构奇异值μ方法设计鲁棒控制器。在设计鲁棒控制系统时,利用μ方法可以很好地降低鲁棒控制系统设计的保守性,控制系统的控制性能更好[20]。
一方面考虑因来流风速引起的垂尾抖振被控系统模态参数的摄动,另一方面考虑垂尾被控系统在辨识建模环节存在着高阶未建模动态特性,将垂尾抖振控制问题转化为图7所示的μ综合控制问题[5]。
外部抖振载荷采用Buffet表示,G0(s)为标称模型,是根据采集的垂尾抖振被控系统辨识输入、输出数据,使用N4SID系统辨识算法[21]辨识得到的12阶连续状态空间模型;Wd为描述抖振载荷干扰特性的权函数;Wu为考虑系统输入的权函数,通过设计Wu可以调整系统的控制输出;Δ1为风速引起的模型参数不确定性集合;Δ2为表述高阶系统未建模动态特性的加性不确定性集合;Wadd为相应的加性不确定性权函数;Wp为描述系统性能指标的加权函数;加速度反馈信号混杂的测量噪声采用n表示,Wn为描述噪声特性的权函数;K为依据结构奇异值μ综合理论设计得到的控制器。
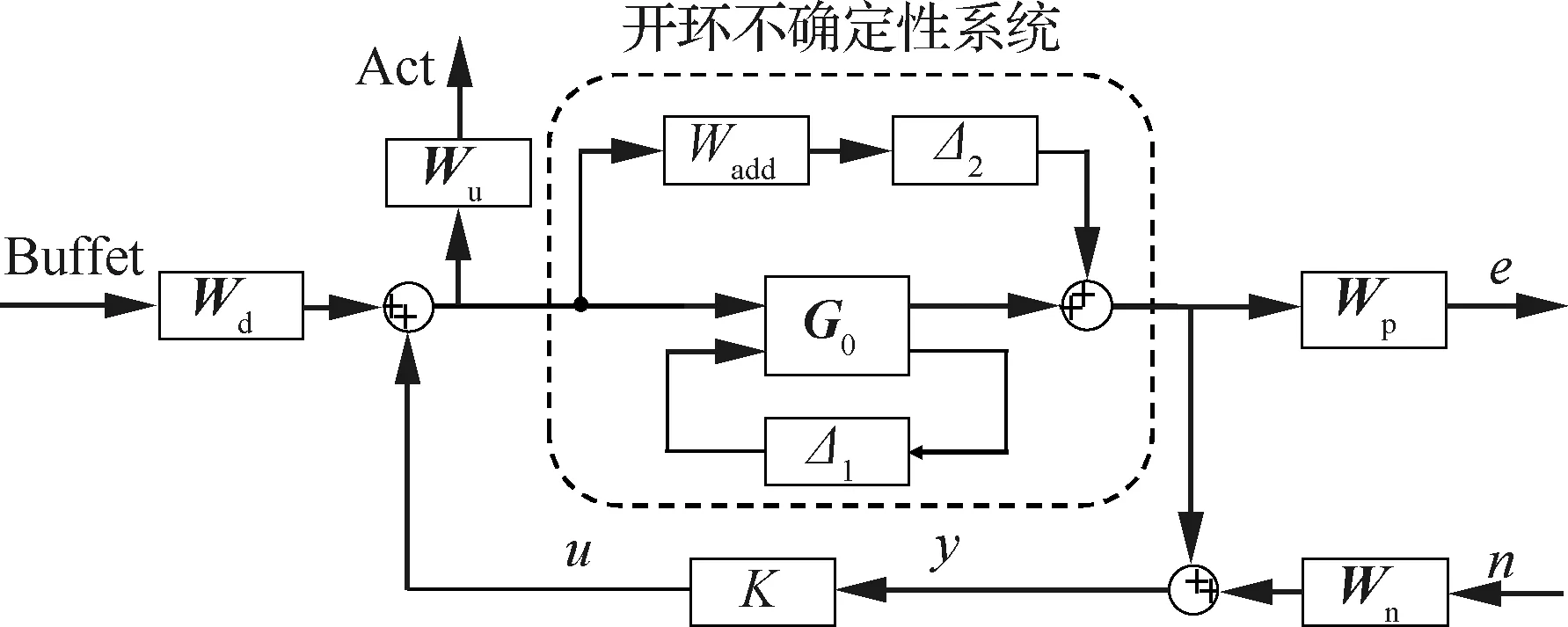
图7 垂尾抖振响应μ综合鲁棒控制原理图Fig.7 Schematic diagram of robust control for vertical tail buffeting
1) 参数不确定性
首先计算来流风速引起的垂尾系统参数不确定性Δ1。试验风洞的最高稳定风速约15 m/s,使用MSC.Nastran软件仿真计算得到考虑非定常气动力的气动刚度效应时,垂尾模型的一阶弯曲模态频率和一阶扭转模态频率随风速变化的曲线,如图8所示。
由图8可见,在0~15 m/s风速范围内,垂尾的一阶弯曲模态频率随风速增加而缓慢单调增大,摄动范围是0~5%;一阶扭转模态频率随风速增加而缓慢单调降低,摄动范围是-2%~0。考虑试验中边界条件的轻微改变等其他不确定性因素的影响,增加控制器设计裕度,将垂尾一阶弯曲模态参数摄动范围设定为-5%~10%,垂尾一阶扭转模态参数摄动范围设定为-10%~5%。

图8 垂尾模型前两阶模态频率随风速变化曲线Fig.8 Diagram of the first two mode frequency varies with wind speed of vertical tail model
2) 加性不确定权函数的设计
对于系统的未建模高阶动态特性,本文采用加性不确定性来描述。标称模型G0(s)采用辨识得到的连续状态空间模型,将试验测试得到的频率响应(即辨识时采用的输入输出数据)作为系统不确定集中的一个元素G(s),然后计算G(s)和G0(s)之差ΔG(s)=G0(s)-G(s),据此画出系统的幅频曲线,随后构造覆盖ΔG(s)的权函数Wadd(s),满足以下不等式:
|Wadd(s)|>|ΔG(s)|=|G0(s)-G(s)|
(11)
根据上述方法得到的加性不确定权函数Wadd(s)的幅频曲线如图9所示,Wadd(s)构造为二阶传递函数:
(12)
3) 其他权函数的选取
干扰特性权函数Wd(s)与系统所受的抖振载荷有关,因此选择带宽为0~45 Hz、增益为1的低通传递函数;输入加权函数Wu(s)用于控制作动器的输入幅值,选择为常值增益;系统噪声特性权函数Wn(s)表示加速度信号采集中混入的噪声,设为常值增益0.01;系统性能指标加权函数Wp(s)是描述系统的灵敏度函数,本文设计为0~45 Hz的低通传递函数,以保证在设计频带内有较大的增益,控制响应更快,传递函数的增益结合输入加权函数Wu(s)共同确定。
4) 鲁棒控制器设计
建立开环不确定系统模型、选择合适的权函数后,利用MATLAB鲁棒控制工具箱,通过D-K迭代方法设计μ综合鲁棒控制器。本文设计的鲁棒控制器阶次为17阶,使用最优Hankel范数近似方法[22]将控制器的阶次降低至10阶。
通过图10所示的开、闭环系统的幅频特性对比,来验证所设计的鲁棒控制器的反馈补偿效果,可以看出,闭环系统(阻尼补偿次级通道)相较于开环系统(次级通道)模态频率处的幅值降低,设计的鲁棒控制器可以明显提高垂尾前两阶模态的阻尼比,一阶弯曲模态的阻尼比由1.1×10-2提升至6.9×10-2,一阶扭转模态的阻尼比由8.7×10-3提升至2.6×10-2。
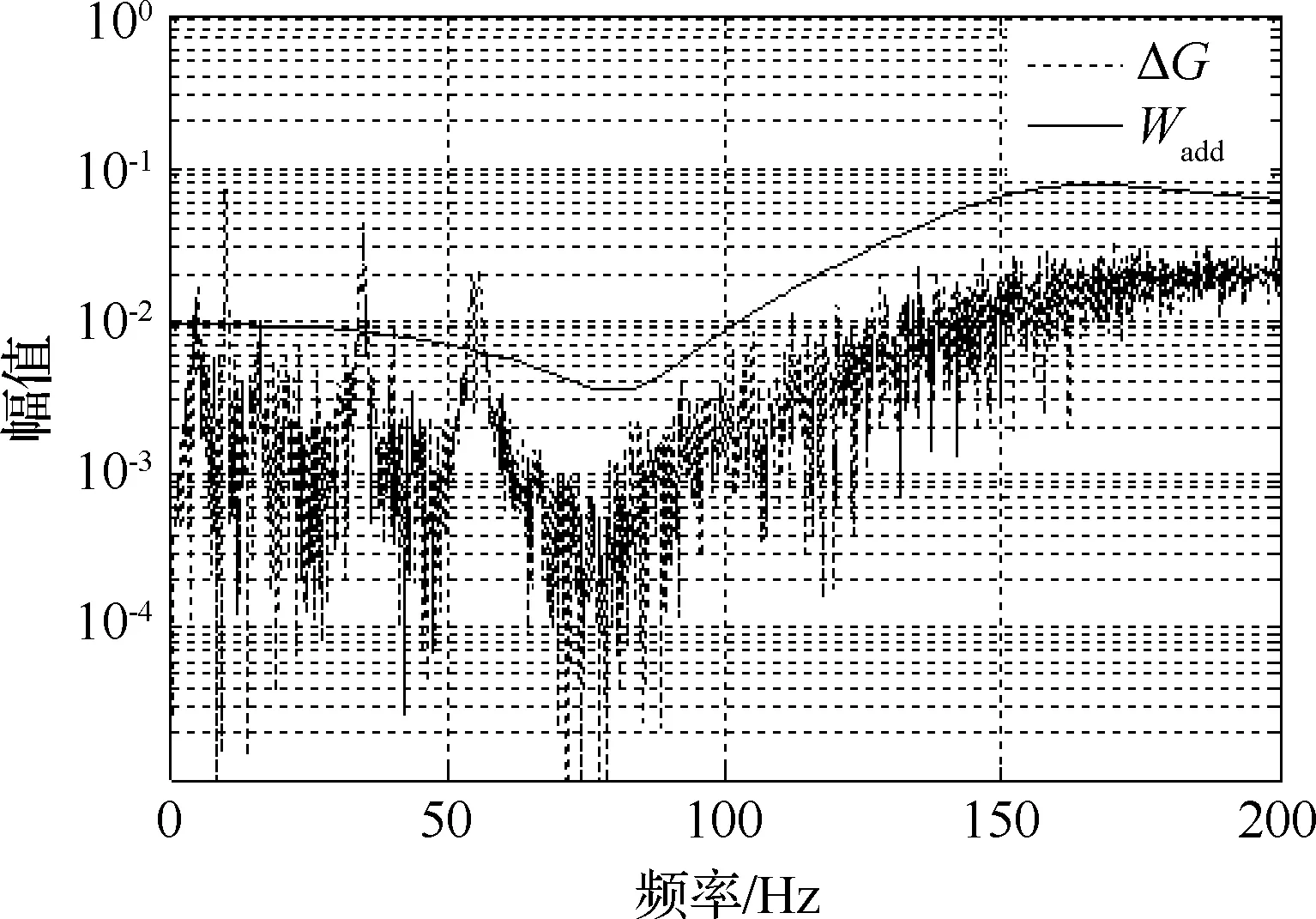
图9 加性不确定权函数的幅频特性曲线Fig.9 Amplitude frequency characteristic curves of additive uncertainty weight function

图10 开、闭环系统幅频特性对比Fig.10 Comparison of amplitude frequency characteristics between open and closed loop systems
3.3 RFxLMS控制器设计
3.3.1 阻尼补偿次级通道辨识
RFxLMS控制器设计需要基于阻尼补偿次级通道(即垂尾被控系统和鲁棒控制器构成的闭环系统)的FIR辨识模型。开展阻尼补偿次级通道的FIR模型离线辨识试验,同样使用图6所示的试验系统,辨识原理如图11所示。

图11 阻尼补偿次级通道的离线辨识Fig.11 Schematic of secondary path damping compensation offline identification
根据采集的输入、输出数据,使用最小二乘法辨识FIR有限脉冲响应模型[23]。垂尾模型前两阶模态的阻尼补偿次级通道辨识结果如图12所示,由于阻尼补偿次级通道是设计鲁棒控制器对原次级通道进行反馈式阻尼补偿得到的,本文又将其与原次级通道的辨识结果对比。为了定量评价辨识结果的精确度,定义吻合度如下:
(13)

原次级通道的辨识模型阶次为1 200阶,与试验模型的吻合度为61.6%;阻尼补偿次级通道的辨识模型阶次为400阶,与试验模型的吻合度为76.6%。次级通道经鲁棒控制器反馈式阻尼补偿后,其辨识模型的阶次降低而辨识精度升高,由于辨识模型的阶次降低,控制算法的计算复杂度也会减小。

图12 阻尼补偿次级通道与原次级通道的FRF辨识结果Fig.12 Frequency response function identification results of original secondary path and damping compensation secondary path
3.3.2 RFxLMS控制器参数
得到阻尼补偿次级通道的辨识模型后,根据图1所示的RFxLMS控制算法原理图设计RFxLMS控制器。其中,自适应控制器的阶次设为32阶,自适应算法中的步长因子在满足收敛性的范围内,为了使控制收敛速度更快,优先选择较大的值,经仿真调试后,设定步长因子为3×10-4。
4 垂尾抖振响应主动控制的地面试验
4.1 单频激励下的振动控制试验
开展单频激励下的垂尾振动响应控制试验,目的是检验和对比控制器的控制性能、收敛速度等特性。试验中,由压电作动器M1a对模型施加模态频率的单频正弦激励,垂尾模型一阶弯曲模态频率为10.0 Hz,一阶扭转模态频率为34.2 Hz,待垂尾处于稳态振动状态后,在第10 s开启控制器驱动压电作动器M1b工作,为了检验控制器的持续稳定性,控制时长设为30 s。
单频激励下,垂尾模型的振动加速度响应在不同控制器控制前、后的时域信号如图13~图15所示,控制效果通过控制前、后垂尾梢部加速度时域信号峰值的幅值比率表示。
试验结果显示,在一阶弯曲模态频率的单频激励下,FxLMS控制器的控制收敛时长约14.2 s,稳定后控制效果达到99%以上;鲁棒控制器响应快速,控制效果为77.5%;RFxLMS控制器的控制收敛时长约2.2 s,远低于FxLMS控制器收敛时长,稳定后控制效果同样达到99%以上。在一阶扭转模态频率的单频激励下,FxLMS控制器的控制收敛时长约16.1 s,稳定后控制效果达到99%以上;鲁棒控制器响应快速,控制效果为33.7%;RFxLMS控制器的控制收敛时长约3.1 s,远低于FxLMS控制器收敛时长,稳定后控制效果也达到99%以上。

图13 单频激励下的垂尾振动响应FxLMS控制时域信号Fig.13 FxLMS control time domain signal of vertical tail vibration response under single frequency excitation

图14 单频激励下的垂尾振动响应鲁棒控制时域信号Fig.14 Robust control time domain signal of vertical tail vibration response under single frequency excitation

图15 单频激励下的垂尾振动响应RFxLMS控制时域信号Fig.15 RFxLMS control time domain signal of vertical tail vibration response under single frequency excitation
单频激励下的振动控制试验表明,FxLMS控制器虽然可以取得很好的控制效果,但是控制收敛时间长;鲁棒控制器的优点是响应快,但控制器的控制效果较差;RFxLMS控制器结合了二者优点,可以快速收敛达到最优控制效果。
4.2 模拟抖振载荷的窄带随机激励控制试验
垂尾抖振是由频谱覆盖垂尾结构低阶模态频率、具有窄带随机特性的脉动非定常气动力所引起一种强迫振动响应,为了检验所设计的RFxLMS控制器对垂尾抖振响应的控制性能,首先用窄带随机激励来模拟垂尾的抖振激励载荷,进行垂尾抖振响应的主动控制试验。进一步对比检验不同控制器对抖振响应的控制性能。窄带随机载荷的频率带宽为5~40 Hz,覆盖了垂尾模型结构的一阶弯曲和一阶扭转模态频率,窄带随机激励载荷信号的功率谱密度(Power Spectral Density, PSD)曲线如图16所示。仍然通过垂尾模型A面根部的压电作动器M1a对结构施加模拟抖振载荷的窄带随机激励,采集时长20 s的无控加速度响应信号,然后开启控制器,采集时长20 s的受控加速度响应信号。

图16 5~40 Hz窄带随机信号的PSD曲线Fig.16 PSD spectrum of 5-40 Hz narrow band random signal
图17~图19为无控响应和分别采用FxLMS控制器、鲁棒控制器、RFxLMS控制器3种控制器进行主动控制后的垂尾梢部加速度响应的PSD曲线。
垂尾抖振响应主动控制的地面模拟试验结果显示,分别采用FxLMS控制器、鲁棒控制器、RFxLMS控制器后,受控加速度响应PSD曲线的一阶弯曲模态频率处峰值分别降低了61.5%、95.3%、97.9%,一阶扭转模态频率处峰值分别降低了55.2%、63.5%、85.8%,相应的加速度响应均方根(Root Mean Square,RMS)值分别降低了14.8%、36.4%、44.0%。可以看出,FxLMS控制器对于模拟抖振的窄带随机振动的控制效果较差,鲁棒控制器的控制效果较好,而RFxLMS控制器具有最好的控制效果。
此外,根据式(14)计算垂尾抖振响应控制过程中不同控制器的离散控制输出信号f(n)的平均功率。
(14)
计算得到,FxLMS控制器、鲁棒控制器、RFxLMS控制器的控制输出信号的平均功率分别为23.6 W、313.2 W、697.9 W,RFxLMS控制器具有更优控制效果的同时输出更多的控制能量,鲁棒控制器的控制输出少于RFxLMS控制器的控制输出,而FxLMS控制器的控制输出较少。

图17 窄带随机激励下垂尾振动响应的FxLMS控制结果Fig.17 FxLMS control results of vertical tail vibration response under narrow band random excitation

图18 窄带随机激励下垂尾振动响应的鲁棒控制结果Fig.18 Robust control results of vertical tail vibration response under narrow band random excitation
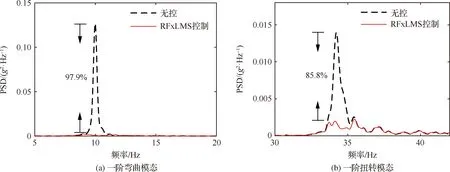
图19 窄带随机激励下垂尾振动响应的RFxLMS控制结果Fig.19 RFxLMS control results of vertical tail vibration response under narrow band random excitation
4.3 地面控制试验总结
FxLMS控制是根据参考信号和振动响应信号在线实时地调节控制器参数,理论上对于周期性的正弦信号可以随着时间推进使振动响应的误差信号逐渐收敛到零,但是对于具有不确定性的窄带随机信号,FxLMS控制器控制效果一般;采用结构奇异值μ方法设计的鲁棒控制器,在控制过程中控制器参数恒定,单频激励下和窄带随机激励下的控制效果是一致的;RFxLMS控制器结合了FxLMS控制器和鲁棒控制器的特点,在单频激励下和窄带随机激励下的控制效果最佳。
地面控制试验表明,经典的FxLMS控制不适用于垂尾抖振这一随机激励下的振动响应控制问题,后续的垂尾抖振响应主动控制的风洞试验中,将对比鲁棒控制器和RFxLMS控制器的抖振响应控制性能。
5 垂尾抖振响应主动控制的风洞试验
5.1 风洞试验工况
垂尾模型抖振响应的主动控制风洞试验中,为了更全面地检验本文所设计控制器的控制性能,需要模拟不同强度的抖振载荷。本文的垂尾模型抖振响应的主动控制风洞试验中,共设置了6个试验工况:风速设为低风速5 m/s、中风速9 m/s 和高风速12 m/s 3种风速,每组风速下扰流翼段的迎角设为30°和60°两种迎角状态。扰流翼段的迎角设置示意图如图20所示。

图20 扰流翼段迎角设置示意图Fig.20 Schematic diagram of attack angle of spoiler wing section
5.2 风洞试验结果
采用鲁棒控制器和RFxLMS控制器进行垂尾模型抖振响应的主动控制风洞试验时,对每个试验工况,首先设置扰流翼段为零迎角状态,开启风洞并调节风速,待风洞的风速稳定工作后,调整扰流翼段到预定的迎角,使垂尾模型产生抖振,然后开启控制器,进行垂尾抖振响应主动控制试验。为了进一步对比鲁棒控制器和RFxLMS控制器的控制性能,在采集时长20 s的垂尾模型无控的抖振响应时域信号后,再打开鲁棒控制器,采集时长为20 s的垂尾模型受控抖振响应时域信号。切换为RFxLMS控制器后,按相同的程序和方法,采集相同时长的垂尾模型在RFxLMS控制器控制下无控和受控的抖振响应时域信号。
图21给出了在扰流翼段不同迎角、不同风速的试验工况下,无控和受控时,垂尾模型梢部后缘加速度响应的PSD曲线对比,PSD曲线使用对数坐标。
由图21可以看出,在给定扰流翼段的迎角下,随着风速的逐渐增大,抖振激励强度增加,垂尾模型在无控情况下的抖振响应也随之增大;相同风速下,随扰流翼段的迎角增大,垂尾模型抖振一阶模态响应明显增大。



图21 垂尾抖振响应主动控制的风洞试验结果对比Fig.21 Comparison of wind tunnel test results of vertical tail buffeting active control
为了定量对比不同控制器的垂尾抖振响应控制性能,重点对比了垂尾模型梢部后缘点的无控和受控加速度响应时域信号的RMS值。表1列出了不同试验工况下,分别采用鲁棒控制器和RFxLMS控制器进行控制后,在2~45 Hz的频率带宽内,垂尾梢部后缘点加速度响应时域信号的RMS值在控制前后的降低量。
从图21和表1中的数据对比可以看出, 采用鲁棒控制器,在扰流翼段60°迎角、5 m/s风速下,垂尾模型抖振响应的RMS降低最多,为41.7%, 在扰流翼段30°迎角、9 m/s风速下,垂尾模型抖振响应的RMS降低最少,为33.5%;而采用RFxLMS控制器,同样是在扰流翼段60°迎角、5 m/s风速下的工况下,垂尾模型抖振响应的RMS降低最多,为48.1%,在扰流翼段30°迎角、12 m/s风速下垂尾模型抖振响应的RMS降低最少,为39.7%。 在扰流翼段迎角、风速都相同的工况下(即相同抖振激励强度下),相比于鲁棒控制器,本文提出的RFxLMS控制器对垂尾模型抖振响应的控制效果更好,显著提升了垂尾抖振主动控制系统的性能。

表1 垂尾抖振响应主动控制的风洞试验结果
6 结 论
1) 基于次级通道阻尼补偿原理,提出了对鲁棒控制器的反馈式次级通道阻尼补偿方法,在FxLMS算法基础上,通过对误差信号的解耦,实现了鲁棒控制器与FxLMS控制算法的结合,得到一种新的RFxLMS控制算法。
2) 针对垂尾结构的抖振响应控制问题,设计了多模态的RFxLMS控制器。开展了垂尾模型抖振响应主动控制的地面模拟试验,验证了RFxLMS控制器的控制性能优于FxLMS控制器和鲁棒控制器的控制性能:相对于FxLMS控制器,RFxLMS具有计算复杂度低、收敛速度快、对随机振动响应控制效果好的优点;相对于鲁棒控制器,RFxLMS控制器在单频激励和随机激励下的控制效果均有提升。
3) 开展了垂尾模型抖振响应主动控制的风洞试验,验证了本文所设计的RFxLMS控制器在多种试验工况下对垂尾模型抖振响应的控制效果显著且稳定,显著提升了垂尾模型抖振主动控制系统的性能。
[21] 李幼凤, 苏宏业, 褚健. 子空间模型辨识方法综述[J]. 化工学报, 2006, 57(3):473-479.
LI Y F, SU H Y, ZHU J. Overview on subspace model identification methods[J]. Journal of Chemical Industry and Engineering, 2006, 57(3):473-479 (in Chinese).

