基于耦合映像格子模型的城市轨道交通网络可靠性研究

朱 岩, 孙 健,2, 王兴举

（1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.上海交通大学 设计学院，上海 200240；3.石家庄铁道大学 交通运输学院，石家庄 050043）

随着我国城市机动化推进及城市交通系统的发展，轨道交通线路不断延伸成网，承担着大规模通勤客流。网络化是轨道交通系统规模效应的体现，从复杂网络视角，建立轨道交通系统网络拓扑结构模型，分析网络客流加权可靠性以及网络毁损级联效应过程，这一研究能够进一步挖掘地铁系统潜在运能，预防故障风险，帮助地铁部门提高路网客流运输能力和应对大规模突发故障。

当前针对轨道交通复杂网络的研究，大多集中在网络鲁棒性、稳定性等静态特性方面，对于地铁网络客流加权网络性质、级联失效[1]等过程的研究相对较少。叶青[2]采用无权静态网络效率等指标，研究重庆市地铁网络拓扑结构脆弱性，发现蓄意攻击对地铁网络效率影响巨大。Sun 等[3]利用网络故障时受影响客流作为指标权重，构建网络脆弱性评价模型，并衡量了上海地铁网络不同线路的脆弱性。谌微微等[4]建立了重庆市轨道交通网络模型，通过中心性等指标，评估网络节点的静态重要性程度。王宇环等[5]基于Space P 空间方法建立南京市轨道交通换乘网络模型，引入行程到达时间指标衡量网络的可达性。以上研究多集中在轨道交通网络脆弱性[6]、可达性等方面。在轨道交通网络可靠性领域，刘志谦等[7]通过聚类系数、平均路径长度等指标，研究了广州地铁网络换乘车站故障对网络可靠性的影响，发现换乘车站故障严重影响出行距离较长的乘客。秦孝敏[8]运用熵权法得出网络效率等不同指标的权重，加权后的指标为最终可靠性评价指标，并利用该指标衡量了重庆市轨道交通网络的可靠性，识别出网络中可靠性较低的站点。丁小兵[9]通过节点间连通性概率、连通效率指标衡量上海轨道交通网络遭受攻击后的连通可靠性变化。上述研究通过不同指标衡量了拓扑结构网络可靠性，但忽略了实际客流因素对网络可靠性的影响。Li 等[10]认为应当从权重角度重新认识网络，并得出网络权重会大幅影响网络性能的结论。刘杰等[11]建立武汉轨道交通网络模型，同时基于出行费用将地铁乘客划分为3 种类型，将网络故障前后受影响的乘客数量作为指标衡量网络可靠性变化。陈峰等[12]以北京市轨道交通OD 客流为权重，利用网络平均最短路径、网络效率等指标，衡量了有权网络在故障发生后的网络可靠性变化。

随后，耦合映像格子（GML）模型[13]开始被应用于描述网络节点时空动力学行为。Xu 等[14]基于CML 模型对全局耦合情形下的无标度网络级联失效过程进行分析，给出网络失效的外部干扰阈值。刘朝阳等[15]利用网络效率指标衡量了北京地铁拓扑结构网络的级联失效过程抗毁性变化，发现地铁具有网络蓄意攻击下抗毁性弱而随机攻击抗毁性较强的特点。黄爱玲[16]改进了CML 模型，将实际客流权重作为参数引入CML 模型，通过建立北京市轨道交通网络模型，探索了客流权重对网络级联失效过程的影响。尹洪英等[17]利用CML 模型分析小范围公路客流网络模型的级联失效过程，提出预测交通网络级联失效影响范围的算法。

综上所述，当前对轨道交通复杂网络的研究大多集中在无权网络静态特性[18]方面，对实际客流加权的轨道交通动力学级联失效过程中可靠性变化研究较少，缺少具体轨道交通网络实例。本文拟通过建立上海市轨道交通网络[19]动力学模型，建立网络客流加权可靠性评价指标，研究网络级联失效过程对客流加权复杂网络可靠性的影响，通过实际案例进一步描述轨道交通网络可靠性变化情况。研究结果可作为地铁部门组织管理地铁客流的依据，以及制定故障应急处置方案的参考。

1 网络客流加权可靠性评价指标

城市轨道交通复杂网络可靠性指网络在部分毁损情况下，剩余网络节点所具有的疏解客流的能力。在级联失效过程中，网络疏解客流功能不断下降，通常引入如下指标评价客流加权网络的可靠性。

1.1 客流加权介数中心性

无权网络节点介数指网络中所有节点对之间的最短路径中经过该节点的数目，常用来评价节点在网络中的枢纽性程度。式（1）为归一化后最短路径条件下节点介数中心性。

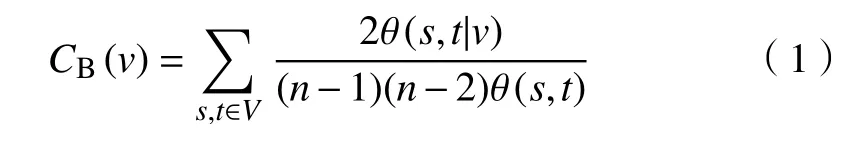
式中：θ（s,t）为从节点s到t的最短路径总数；θ（s,t|v）为除路径s到t外，全部最短路径中经过节点v的路径数，若s=t，则θ（s,t）=1；n为网络节点数；V为全部网络站点集合。

然而，无权网络中介数大的节点，在加权真实客流后，未必仍然具有较大枢纽性。因此，客流加权网络节点介数指经过该站点的单日客流权重与归一化后无权介数的乘积，如式（2）所示。地铁网络整体客流加权介数可表示为全部节点加权介数均值，如式（4）所示。

1.2 熵与网络客流强度熵

熵（Entropy）是表征系统混乱程度的函数，熵值越大，表明系统的混乱程度越高。谭跃进等[20]提出网络结构熵指标衡量无权网络均匀程度。

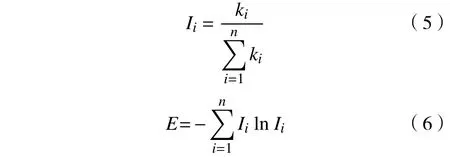
式中：ki为第i个节点度值；Ii为第i个节点度值占全部节点度值总和的比例；E为无权网络结构熵值。

刘宝全等[21]利用网络强度熵来衡量地铁加权网络的客流混乱程度。通过引入站点客流强度作为轨道交通网络节点权重，利用网络权重熵衡量网络节点服务客流强度的均匀程度，经过归一化可得标准网络客流强度熵为

2 基于CML 的 轨 道交通 网 络系统建模与统计分析

2.1 耦合映像格子（CML）模型

CML 模型定义了系统网络节点之间的耦合作用机制，同时可反映系统在级联失效过程中的扩散效应，被广泛应用于复杂系统动力学研究[22]。具体形式如下：

式中：Xi（t）是节点i在t时刻的状态；ε为耦合系数；k（i）为节点度，是指与该节点直接相连的其他节点的数目；aij为表示网络连接信息邻接矩阵中对应的i行j列元素，aij=1 表示节点i与节点j直接相连，aij=0 表示两节点不直接相连；f（x）为混沌Logistic 映射函数，其值域变化范围在（0,1）之间。

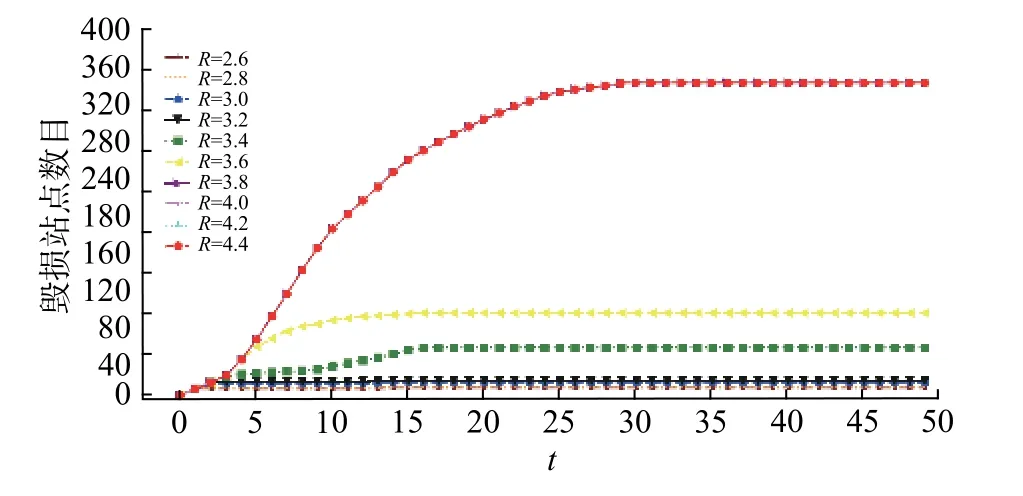
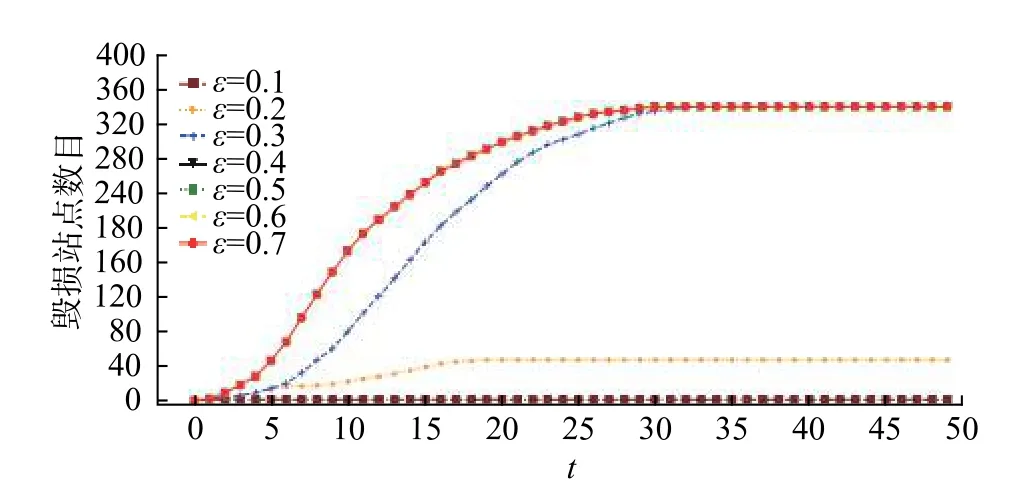
Xi（t+1）由式（9）运算后得到，当0

失效节点i将在m+1 时刻从网络中移除，其后时间步i节点状态值均为0。由于CML 模型具有故障传播机制，下一时刻i的相邻节点将受到影响并可能导致故障，继而触发网络级联失效过程。

2.2 CML 模型条件下网络节点时空状态

2.2.1 健康状态下网络节点CML 状态值时空变化

CML 模型描述了网络中节点状态与节点之间的作用关系，即节点当前时间步的状态值仅受上一时刻状态以及相邻节点状态影响，每个网络节点在任一时间步均有各自状态值Xi（t）。初始时刻t=0 时，网络中所有节点各自状态值Xi（0）被设置为（0,1）之间的随机值；下一时刻t=1 时，节点状态值Xi（1）由t=0 时刻节点状态值Xi（0）以及节点i的相邻节点集合Xj（0）依据式（9）计算得出，全部网络节点在t=1 时刻状态值同样依据式（9）计算更新一次。继续上述过程，可得全部时间步网络节点CML 值。当网络节点未受干扰时，节点状态值始终为（0，1）范围内的健康状态。以上海地铁5 号线东川路地铁站节点为例，东川路节点各时间步的CML 状态均受到其相邻节点剑川路、江川路CML 状态值影响，在未施加干扰R情况下，其CML 状态值变化如图1 所示。

图1 未施加干扰R 时东川路节点CML 状态值随时间步变化情况Fig.1 CML state value changes of Dongchuan Road station node by time steps without disturbance R

由图1 可知，东川路节点在未施加干扰情形下，处于正常状态时，CML 状态值始终介于（0，1）之间。

2.2.2 施加干扰R≥1 情况下网络节点CML 状态值

随机选择某节点S，在m时刻施加扰动R≥1而导致故障，S为失效节点。m+1 时刻，S节点因故障从网络中移除，此后S节点状态值被设置为0。此时，S节点的相邻节点首先受到影响，并可能导致故障。若S的相邻节点G在m+1 时刻被传染并出现故障，故障不断向其相邻节点传播，直至网络中不再出现新的故障节点，故障传播停止。仍以东川路地铁站节点为例，在第51 个时间步施加干扰R=1，节点失效，其CML 状态变化如图2 所示。

图2 施加干扰R=1 时东川路节点CML 状态值随时间步变化情况Fig.2 CML state value changes of Dongchuan Road station node by time steps with disturbance R =1,

图2 表明，施加干扰R=1 后，东川路状态值超过临界值1，表明节点失效，并在系统规则条件下，于下一时间步从网络中移除，其后时间步，该节点CML 状态值均为0。由网络节点在不同时间步的健康与失效状态，可以描述出网络的级联失效动力学过程。

2.3 上海市轨道交通网络动力学模型构建

类似于东川路地铁站节点，CML 模型条件下，每个网络节点均为独立的动力学单元，全部网络节点构成网络动力学模型。利用L 空间方法（Space L）建立站—站模型，即地铁站点为网络节点，站点若直接相连，则网络中有一条无向边相连接。以上海市轨道交通网络为例，截至2018 年12 月，上海市轨道交通网络具有运营线路16 条，共415 个站点，将换乘站点看作一个网络节点，则上海地铁网络模型共有341 个网络节点。以徐家汇站及周边站点为例，连接关系如图3 所示。

图3 基于Space L 方法的徐家汇站拓扑关系图Fig.3 Topological relationship diagram of Xujiahui station based on Space L method

2.4 基于CML 模型网络级联失效可靠性评价算法流程

级联失效过程中不同时间步、网络节点CML状态值、网络失效节点数以及客流加权网络稳定性，由如下算法流程得到：

步骤1基于Dijkstra 最短路算法将实际日客流分配到地铁网络，统计通过网络节点客流介数Qv。

步骤2设置网络全部节点的初始状态值Xi（0）为（0,1）之间的随机值，并随机选取一个网络节点施加扰动R≥1，节点失效；并根据式（4）和（7）分别计算并记录当前时间步网络客流加权介数、网络客流加权强度等属性值。

步骤3统计上一时间步全部节点CML 状态值，当节点状态值Xi（t）≥1 时，为失效节点，并移除该节点。剩余网络节点CML 状态值基于式（9）更新一次；统计并记录当前时间步网络客流加权介数、客流加权熵等属性值。

步骤4重复步骤3，直至网络故障节点数不再变化。

步骤5当网络故障节点数不再变化，网络处于新的稳定状态。统计网络客流加权介数、客流加权熵等属性值。

步骤6输出各时间步记录的统计结果。

3 上海轨道交通系统网络级联失效过程可靠性分析

3.1 上海公共交通一卡通大数据处理与统计

通常地铁乘客选择轨道交通网络中最短路径出行，通过对地铁一卡通数据的筛选、排序等预处理后，基于Dijkstra 最短路算法，将上海地铁2016 年8 月29 日约500 万人次客流，按每人次行程起讫点，逐一分配至地铁网络关系模型中。对于任意单次行程，由起点至终点所经过的多个站点，均被认为服务过一次出行。经过全部单日客流逐次叠加，统计经过某站点v的实际客流数Qv，作为计算客流加权指标的权重。网络节点客流Qv体现了节点客流加权的重要程度。根据式（1）和式（2）分别得到上海市轨道交通无权与客流加权网络介数排名前十位的节点，如表1 所示。

表1 上海地铁网络节点无权与客流加权介数对比表Tab.1 Comparison of unweighted betweenness and passenger flow weighted betweenness

表1 中，节点客流加权后的介数与静态介数差别较大。如上海火车站，其静态介数值较低，表明上海火车站节点在无权路网中的枢纽性较低，但由于其承担大量城际交通客流，客流加权介数值较大，在客流加权路网中枢纽性大幅上升。这表明实际客流权重对网络介数等性质产生较大影响。

3.2 轨道交通网络级联失效过程中客流加权可靠性变化分析

在不同节点度、耦合系数ε以及干扰值R因素影响下，轨道交通网络系统级联失效过程表现不同，相应的网络可靠状态也存在差别。R干扰太小往往不能导致网络的连锁崩塌，耦合系数ε过大会导致网络干扰传播速度过快，而节点度则主要描述了节点位置对网络级联失效的影响。对上述不同因素进行分析，可发现不同因素导致的客流加权性质的变化情况。

3.2.1 节点度（Degree）对客流加权网络级联失效的影响

度指与节点相连边的数量，其值主要衡量节点在网络中的位置因素。度值越大的节点，其网络中重要性越高。对地铁网络而言，度值大的节点往往位于网络中心区域，值较小的节点往往在网络边缘。为研究不同度值节点对网络级联失效过程的影响，分别选取上海市浦东国际机场（度值D为1），剑川路（度值D为2）、蓝村路（度值D为3）、西藏南路（度值D为4）4 个地铁站点，在耦合系数ε=0.2 情形下，施加相同干扰R=4，可得网络节点毁损过程及可靠性变化如图4 所示。

图4 R=4，ε=0.2 时，不同度值节点导致网络级联失效过程图Fig.4 Network cascading failure processes caused by stations under different degree values when R=4, ε=0.2

图4 对比了不同度值节点引发地铁网络级联失效的过程，图5（a），5（b）分别衡量级联失效过程中客流加权网络介数可靠性、客流加权熵可靠性变化。在干扰R和耦合系数ε相同情况下，故障节点度值越大，干扰R传播越快，网络毁损速度越快。t≤5 时，地铁网络毁损过程处于初始阶段，干扰R仅能传播至失效节点的相邻节点，传播速度较慢。此阶段，网络客流加权介数与客流加权熵受到影响较小，表明网络功能基本未受影响。当t>5 时，由于干扰传播至网络中心，通过换乘节点传播至其他线路，网络开始加速毁损，最终导致干扰扩散，全部节点均被传染并发生故障。在加速阶段，加权熵值不断下降，表明客流混乱度不断下降，客流受到影响呈加速扩大趋势，如图5（b）。与加权熵不同，网络客流加权介数下降速度更快，位于中心区域节点的毁损导致网络连通性质几何级下降。同时，中心区域节点客流量较大，当网络毁损规模达到一半时，网络基本失去连通性能，网络客流加权介数下降至0 附近。

图5 R=4，ε=0.2 时，不同度值节点导致网络级联失效过程的客流加权可靠性变化图Fig.5 Changes on the reliability of passenger flow weighted network during cascading failure processes caused by stations under different degree values when R =4， ε =0.2

可以发现，节点度值主要影响网络级联失效过程的干扰传播速度。因此，重点维护网络中度值高的节点对防范网络系统性风险具有较大意义。

3.2.2 不同R干扰对客流加权网络级联失效可靠性的影响

R干扰主要衡量了节点故障程度的大小。系统网络在不同R值干扰情况下，表现出可靠到崩塌的不同情形。R值较小不会引起网络连锁毁损，R值较大时，网络则会连续毁损。为凸显不同R值对网络级联失效过程的影响，选取网络中度值最大的节点，世纪大道站（D=6）分别施加不同扰动值R（2.6～4.4），分析网络级联失效过程，如图6所示。

图6 ε=0.2 时，世纪大道站在不同R 值干扰下导致网络级联失效过程图Fig.6 Network cascading failure processes caused by Century Avenue station under different R value disturbance when ε=0.2

图6 描述了地铁世纪大道节点在不同R干扰下，引发级联失效过程的范围与速度。当R≤3.6时，不足以导致连续的网络崩塌，仅少数节点发生故障。随着R值增大，系统出现崩塌效应，绝大部分网络节点因故障传播而失效，仅有少数节点保持正常。当R>3.6 时，网络出现连锁崩塌且传播能力增强，每一时间步与失效节点相邻的节点均被感染并失效。

图7（a），7（b）分别显示网络客流加权介数、客流加权熵可靠性在相应级联失效过程中的变化情况。在级联失效过程中，客流加权介数可靠性总体不断下降，但在10≤t≤20，R=3.4，3.6 时，客流加权介数可靠性小幅上升，这表明某些多余节点的故障，能够提高网络整体连通性。客流加权熵指标下降幅度总体符合级联失效过程，表明网络节点服务客流的均匀程度受级联失效影响相对较小。

综上所述，R干扰主要影响了网络级联失效的规模，同时存在导致网络故障扩散的临界值，因此，应当重点防范轨道交通系统可能发生的大型事故。

3.2.3 不同耦合系数ε对客流加权网络级联失效可靠性的影响

耦合系数ε值衡量了网络节点之间作用关系的强弱。ε较大，表明节点间的作用关系强，干扰传染能力强；ε较小，则表示节点间作用关系弱，干扰传染能力差。ε的大小同样影响故障的传播能力。随机选取网络中度值为2 的节点，如浦东大道站。在不同ε条件下，分别施加R=4，可得网络级联失效过程如图8 所示。

图7 ε=0.2 时，世纪大道站在不同R 值干扰下导致网络级联失效过程中的客流加权可靠性变化图Fig.7 Changes on the reliability of passenger flow weighted network during cascading failure processes caused by Century Avenue station under different R value disturbance when ε=0.2

图8 R=4 时，浦东大道站在不同ε 值干扰下网络级联失效过程图Fig.8 Network cascading failure processes caused by Pudong Avenue station under different ε value disturbance when R=4

图8 描述R=4 时，浦东大道节点在不同ε干扰下，引发级联失效过程的范围与速度。当ε≤0.2时，仅部分节点发生故障，不会导致网络连续崩塌；ε>0.2 时，会引起网络崩塌连锁反应；ε>0.3时，级联失效图重合，网络级联失效过程达到最大速度。由图9（a），（b）可知，相比客流加权熵，客流加权介数可靠性下降速度更快，表明网络整体连通性下降更快。与图7 结论类似，网络客流加权介数值在缺少某些冗余节点后，反而提高了网络整体连通性。

综上所述，耦合系数ε通过影响R在传播过程中的大小，来影响网络级联失效的规模与速度。因此，降低网络故障传播耦合系数ε，可有效防止轨道交通网络级联失效扩散。

4 结束语

考虑真实客流对加权网络可靠性的影响，构建了网络客流加权可靠性评价指标。利用上海地铁一卡通数据，以实际客流权重为参数，统计并分析轨道交通网络节点介数及其客流加权网络介数，得出客流权重大幅影响网络可靠性的结论。

建立了基于CML 模型的地铁网络动力学模型，研究不同因素对地铁网络级联失效过程的影响。结果表明，客流加权网络中度越大的节点其故障传播能力越强，传播速度越快。耦合因子越大，网络级联失效过程越快。网络节点受到干扰过大，将会导致网络崩塌效应。

衡量了上海地铁网络级联失效过程的客流加权可靠性动态变化情况。相比网络客流加权熵可靠性，网络客流加权介数可靠性衰减速度快，当毁损规模过半，网络客流加权可靠性将趋近于0，表明网络连通性质下降更快。

本文所利用的客流权重为单日客流经分配后的累计值，未能充分体现地铁站点在单日内不同时段加权可靠性动态变化情况，未来可进一步针对不同时段地铁站点客流加权可靠性变化问题进行深入研究。